Kezdőlap


Cím:	Az 1994. évi (25.) Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Gnädig Péter
Füzet:	1994/november, 458 - 470. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elméleti verseny^{$^{*}$}

1. feladat. Relativisztikus részecske
A speciális relativitáselmélet alapján egy

m_{0}

nyugalmi tömegű szabad részecske

E

energiája és

p

lendülete között a következő összefüggés érvényes:

\begin{matrix} E = \sqrt[]{p^{2} c^{2} + m_{0}^{2} c^{4}} = m \cdot c^{2} . \end{matrix}

Ha egy részecske konzervatív erőtérben van, a részecske teljes energiája, ami a

\sqrt[]{p^{2} c^{2} + m_{0}^{2} c^{4}}

tag és a potenciális energia összege, állandó marad. Ha a részecske energiája nagyon nagy, a nyugalmi energiája elhanyagolható (az ilyen részecskét ultrarelativisztikusnak nevezzük).
1. Tekintsük egy nagyon nagy energiájú részecske (melynek nyugalmi energiája elhanyagolható) egydimenziós mozgását, amelyre állandó

f

nagyságú, centrális, vonzóerő hat. Tegyük fel, hogy a részecskét a

t = 0

kezdőpillanatban

p_{0}

kezdeti lendülettel az erőcentrumba helyezzük. Írd le a részecske mozgását két különböző módon: először a

p

lendületet ábrázold az

x

térkoordináta függvényében, majd

x

-et ábrázold

t

függvényében, legalább a mozgás egy periódusában. Határozd meg a fordulópontok koordinátáit a

p_{0}

és az

f

paraméterek segítségével, valamint nyilakkal ábrázold a mozgás irányát a

p - x

diagramon.
Megjegyzés. A mozgás közben lehetnek olyan rövid idő-intervallumok, amikor a részecske nem ultrarelativisztikus. Ezeket az időtartamokat azonban hanyagoljuk el!
2. A mezonok két kvarkból felépülő részecskék. A mezon

M

nyugalmi tömege megegyezik a 2-kvark rendszer teljes energiájának

c^{2}

-ed részével.
Tekintsük egy nyugalomban lévő mezon olyan egydimenziós modelljét, amelyben a 2 kvarkról feltesszük, hogy az

x

tengely mentén mozognak, és állandó nagyságú

f

erővel vonzzák egymást. Azt is feltételezzük, hogy egymáson szabadon áthatolhatnak. A kvarkok nagyenergiájú mozgásának leírásakor a kvarkok nyugalmi tömege elhanyagolható.
A

t = 0

kezdőpillanatban mindkét kvark az

x = 0

helyen található. Add meg a 2 kvark mozgását grafikusan az

x - t

és a

p - x

diagramokon. Határozd meg a fordulópontok koordinátáit

M

és

f

segítségével. Jelöld be a folyamat irányát a

p - x

diagramon, és végül határozd meg a 2 kvark közötti maximális távolságot!
3. Az előző alkérdésben használt vonatkoztatási rendszert

S

rendszernek nevezzük. Az

S'

-vel jelölt laboratóriumi vonatkoztatási rendszer a negatív

x

irányba mozog

V = 0,6 c

állandó sebességgel. A két vonatkoztatási rendszerben a koordinátákat úgy választjuk meg, hogy az

x = 0

pont essen egybe az

S'

-beli

x' = 0

ponttal a

t = t' = 0

kezdőpillanatban.
Ábrázold grafikusan a 2 kvark mozgását az

x' - t'

grafikonon, határozd meg a fordulópontokat

M

f

és

c

segítségével, és végül számítsd ki a két kvark között az

S'

laboratóriumi rendszerben észlelhető maximális távolságot!
Megjegyzés. Az

S

és az

S'

koordináta-rendszerek között a Lorentz-transzformáció teremt kapcsolatot:

\begin{matrix} {\begin{matrix} x' & = γ (x + β c t) \\ t' & = γ (t + β \frac{x}{c}), \end{matrix} \end{matrix}

ahol

V

a két koordináta-rendszer sebessége,

β = V / c

és

γ = \frac{1}{\sqrt[]{1 - β^{2}}}

.
4. Egy mezon nyugalmi energiája

M c^{2} = 140 MeV

, sebessége pedig 0,6 c az

S'

laboratóriumi rendszerhez viszonyítva.
Határozd meg az

S'

laboratóriumi rendszerben a mezon

E'

energiáját!
Megoldás. 1. A vonzócentrumot az

x = 0

pontba helyezve a potenciális energia

U (x) = f | x |

módon adható meg. A teljes energia ekkor

\begin{matrix} E = \sqrt[]{p^{2} c^{2} + m_{0}^{2} c^{4}} + f | x |, \end{matrix}

ami ultrarelativisztikus határesetben:

E = | p | c + f | x |

. Ez az összefüggés egyben a részecske ,,fázisgörbéje'' a

p - x

síkon. (1. ábra). A részecske összenergiáját az

\begin{matrix} E (x = 0, p = p_{0}) = p_{0} c \end{matrix}

összefüggés, a fordulópontot pedig az

E (| x | = L, p = 0) = p_{0} c

egyenlet adja meg:

L = p_{0} c / f

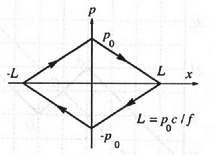1. ábra

Ultrarelativisztikus (

E > > m_{0} c^{2}

) határesetben a részecske

p = \frac{m_{0} v}{\sqrt[]{1 - v^{2} / c^{2}}}

lendülete csak úgy lehet véges nagyságú, ha

| v | \approx c

. Ugyanerre a következtetésre juthatunk az

F = Δ p / Δ t

Newton-egyenletből is:

\begin{matrix} | v | = | \frac{Δ x}{Δ t} | = | \frac{Δ p}{Δ t} | \cdot | \frac{Δ x}{Δ p} | = f \cdot \frac{L}{p_{0}} = c . \end{matrix}

A részecske tehát

v \approx \pm c

sebességgel mozog

x = \pm L

pontok között (leszámítva a fordulópontok közelében eltöltött rövid időt), ahogy az a 2. ábrán látható. A periódikus mozgás negyed periódusideje:

τ = L / c = p_{0} / f

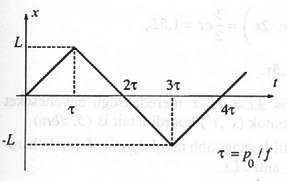2. ábra

2. A két kvarkból álló rendszerre az energiatétel:

\begin{matrix} M c^{2} = | p_{1} | c + | p_{2} | c + f | x_{1} - x_{2} |, \end{matrix}

ahol

x_{i}

és

p_{i}

az egyes kvarkok helye, illetve lendülete (

i = 1,2

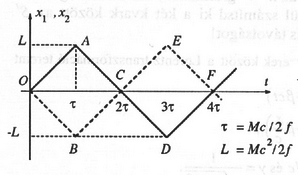3. ábra

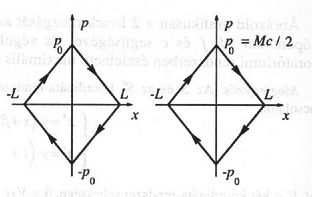4. ábra

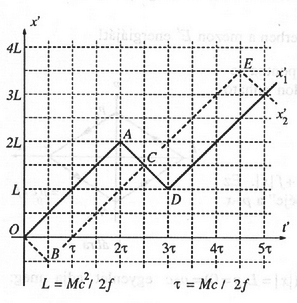5. ábra

A mezon tömegközépponti koordináta-rendszerében

p_{1} + p_{2} = 0

, emiatt

p_{1} = - p_{2}

és

x_{1} = - x_{2}

. A megfelelő diagramok az előző alponthoz hasonlóan kaphatók (3. és 4. ábra). A legnagyobb távolság a kvarkok között:

d = 2 L = M c^{2} / f

. (A

p - x

diagramon a körüljárások iránya azonos, de a 2 kvark között ,,fáziskésés'' van.)
3. A két részecske az

S'

vonatkoztatási rendszerben is (jó közelítéssel)

\pm c

sebességgel mozog. Ha az

x' = 0

;

t = 0

origónak a kvarkok találkozási ,,eseményét'' választjuk (

O

pont a 3. ábrán), akkor a következő találkozó

C

eseménye, amelyet

x_{1} = x_{2} = 0

és

t = 2 τ = M c / f

jellemez, az

S'

rendszerben (

v = 0,6 c

, azaz

β = 3 / 5

γ = 5 / 4

felhasználásával)

\begin{matrix} x' & = γ (x + β c t) = \frac{5}{4} (O + \frac{3}{5} c \cdot 2 τ) = \frac{3}{2} c τ = 1,5 L, \\ y' & = γ (t + β \frac{x}{c}) = \frac{5}{4} \cdot 2 τ = 2,5 τ . \end{matrix}

O

és

C

pontokból ,,fénysebességű'', vagyis

\pm c = \pm L / τ

meredekségű egyeneseket húzva megkapjuk az

A, B, E, D ...

fordulópontok

(x', t')

koordinátáit is (5. ábra).
Erről leolvasható, hogy a részecskék közötti legnagyobb távolság

d' = L

(ez láthatóan kisebb, mint az

S

-ben legnagyobb távolság, ami

2 L

).
4. Ha egy

E = M c^{2} = 140 MeV

energiájú mezon

v = 0,6 c

sebességgel mozog a laborrendszerhez képest, akkor az impulzusa a laborban

\begin{matrix} p' = \frac{M v}{\sqrt[]{1 - v^{2} / c^{2}}} = \frac{M \cdot 0,6 c}{\sqrt[]{1 - 0, 6^{2}}} = \frac{3}{4} M c, \end{matrix}

az energiája pedig ugyanebben az

S'

rendszerben

\begin{matrix} E' = \sqrt[]{p'^{2} c^{2} + M^{2} c^{2}} = M c^{2} \sqrt[]{\frac{9}{16} + 1} = \frac{5}{4} M c^{2} = 175 MeV . \end{matrix}

2. feladat. Szupravezető mágnes

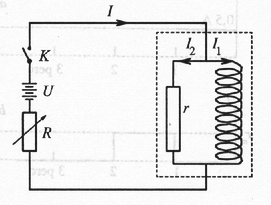6. ábra

A szupravezető mágnességet széles körben használják a laboratóriumokban. A szupravezető mágnesek legelterjedtebb alakja egy tekercs (szolenoid), amely szupravezető drótból készült. A szupravezető mágnesek csodálatos előnye, hogy nagy mágneses teret hoznak létre, miközben nincsen Joule-hő okozta energiaveszteség, mivel a szupravezető drót elektromos ellenállása nullává válik, amikor a mágnes 4,2 K hőmérsékletű folyékony héliumba mártjuk. A mágneshez rendszerint hozzátartozik egy speciális szupravezető kapcsoló, amint ezt a 6. ábra mutatja. A kapcsoló

r

ellenállása szabályozható: vagy

r = 0

szupravezető állapotban, vagy

r = r_{n}

normál állapotban van. Amikor a kapcsoló szupravezető állapotban van, a mágnesen állandó erősségű áram folyik, amelynek nagysága akármekkora lehet. A szupravezető állapotba hozott kapcsolóval elérhetjük, hogy még hosszú idővel a külső áramforrás kikapcsolása után is állandó mágneses mező maradjon a tekercsben.
A szupravezető kapcsoló részletei nem láthatók a 6. ábrán. Ez általában egy rövid szupravezető huzal, amelyet fűtőszál vesz körül, és megfelelően hőszigetelve van a folyékony héliumtól. Fűtés hatására a szupravezető huzal hőmérséklete növekszik, így normál állapotú ellenállássá változik. Az

r_{n}

tipikus értéke néhány ohm, esetünkben 5 ohm. A szupravezető mágnes önindukciós együtthatója a méretétől függ, a 6. ábrán látható mágnes esetében tekintsük 10 H-nek. A teljes

I

áramot az

R

ellenállás segítségével változtatjuk.

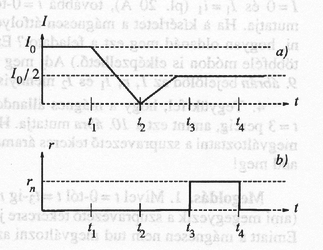7. ábra

A nyilak az

I

I_{1}

és

I_{2}

pozitív irányait jelölik.
1. Ha a teljes

I

áramot és az

r

ellenállású szupravezető kapcsoló áramát a 7(a) és 7(b) ábrán látható módon változtatjuk, és feltehetjük, hogy a mágnesen és a kapcsolón átfolyó

I_{1}

és

I_{2}

áramok kezdetben egyenlők voltak, határozd meg, hogyan változnak ezek időben

t_{1}

-től

t_{4}

-ig. A válaszodat hasonló ábrákon tüntetsd fel. (Ezen feladat értékelésénél csak az általad megadott grafikonokat veszik figyelembe!)
2. Tegyük fel, hogy a

K

tápfeszültségkapcsolót a

t = 0

pillanatban bekapcsoljuk, amikor

r = 0

I_{1} = 0

és

R = 7,5 Ω

, továbbá a teljes

I

áram 0,5 A. A

K

kapcsoló zárvatartása mellett a szupravezető kapcsoló

r

ellenállása a 8(b) ábra szerint változik. Add meg a 8(a), 8(c), 8(d) ábrákon a megfelelő

I

I_{1}

és

I_{2}

áramok időbeli változását!

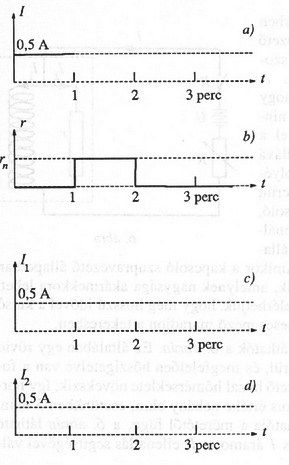8. ábra

9. ábra

3. Normál állapotban a szupravezető kapcsolón csak kis áramok folyhatnak át, nevezetesen csak 0,5 A-nél kisebb, mert máskülönben a nagy áramok kiégetik a kapcsolót. Tegyük fel, hogy a szupravezető mágnes állandósult (bekapcsolt) állapotban van, azaz

I = 0

és

I_{1} = i_{1}

(pl. 20 A), továbbá

t = 0

-tól

t = 3

percig

I_{2} = - i_{1}

, amint ezt a 9. ábra mutatja. Ha a kísérletet a mágnesen átfolyó áram zérusra csökkentésével be kell fejezni, hogyan oldanád meg ezt a feladatot? Ezt néhány lépésben teheted meg. (Az eljárás többféle módon is elképzelhető.) Adj meg egy lehetséges megoldást olymódon, hogy a 9. ábrán bejelölöd az

I

r

I_{1}

és

I_{2}

mennyiségek időbeli változását.
4. Tegyük fel, hogy a mágnes állandó, 20 A-es áramerősséggel működik

t = 0

-tól

t = 3

percig, amint ezt a 10. ábra mutatja. Hogyan tudnád az említett feltétel betartásával megváltoztatni a szupravezető tekercs áramát 30 A-re? Válaszodat a 10. ábrán grafikusan add meg!

10. ábra

Megoldás. 1. Mivel

t = 0

-tól

t = t_{3}

-ig

r = 0

, a szupravezető kapcsolón eső feszültség (ami megegyezik a szupravezető tekercsre jutó

L d I_{1} / d t

feszültséggel) nulla kell legyen. Emiatt a mágnesen nem tud megváltozni az áramerősség, tehát

\begin{matrix} I_{1} (t) = I_{1} (t_{0}) = \frac{1}{2} I_{0}, \end{matrix}

illetve

\begin{matrix} I_{2} (t) = I (t) - I_{1} (t) = I (t) - \frac{1}{2} I_{0} . \end{matrix}

Mivel

t = t_{3}

-kor

I_{2} = 0

, a kapcsoló normál állapotba kerülése után sem esik feszültség rajta, tehát a tekercs árama a továbbiakban sem változik (11. ábra).

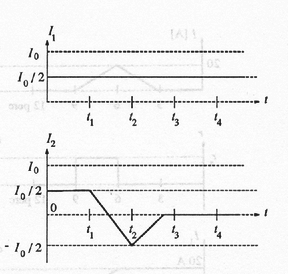11. ábra

12. ábra

2. Az első 1 percben

I_{1}

nem tud megváltozni (hiszen

r = 0

), s mivel a teljes

I

sem változik,

I_{2}

is konstans marad.

t = 1

percnél

r

hirtelen felugrik 0-ról

r_{n}

-re,

I

lecsökken

U / R

-ről

U / (R + r_{n})

-re, a megadott számadatokkal 0,3 A-re.

t = 1

és 2 perc között

I

I_{1}

és

I_{2}

fokozatosan tart az egyensúlyi állapotnak megfelelő értékekhez (ezek:

I = U / R = 0,5 A

I_{1} = I = 0,5 A

és

I_{2} = 0

). Az időállandó

\begin{matrix} τ = \frac{L (R + r_{n})}{R r_{n}} = 3 s, \end{matrix}

ami elég rövid ahhoz, hogy

t = 2

perckor (60 s múlva) az áramerősségeket már az egyensúlyi értékekkel azonosnak tekinthessük. Ezután a szupravezető kapcsoló ismét

r = 0

ellenállású lesz, de ez nem változtat a konstans áramértékeken, hiszen rajta úgysem esett feszültség (12. ábra).
3. Első lépés: A

K

főkapcsoló zárt állása mellett fokozatosan megnöveljük az áramkör teljes

I

áramát 20 A-rel. Mivel a szupravezető kapcsoló

r = 0

állapotban van, a tekercs árama nem változhat meg, tehát

I_{2}

20 amperrel megnő, bagyis -20 A-ról nullává válik. Második lépés: A szupravezető kapcsolót kikapcsoljuk (

r = r_{n}

normál állapotba hozzuk). Harmadik lépés: Az eredő áramerősséget fokozatosan nullára csökkentjük, ezzel egyúttal a tekercsen átfolyó áramot is nullává tesszük. A csökkentés ütemét az korlátozza, hogy

L d I_{1} / d t

indukált feszültség nem lehet nagyobb, mint

r_{n} = 5 Ω

és a megengedett maximális 0,5 A szorzata, 2,5 V. Mivel

L = 10 H

d I_{1} / d t < 0,25 A / s

. A tekercs árama tehát percenként legfeljebb 15 ampernyit változhat. Negyedik lépés: Az

r

szupravezető kapcsolót ismét bekapcsoljuk, a főkapcsolót pedig kikapcsoljuk. Az egész folyamat a 13. ábrán látható.

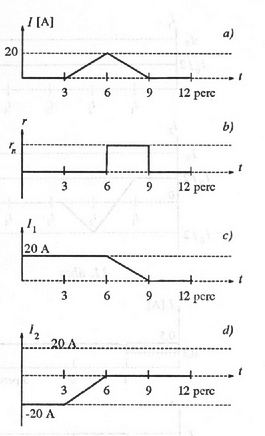13. ábra

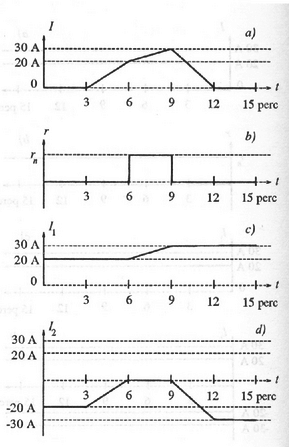14. ábra

4. Az első és a második lépés ugyanaz, mint az előző kérdésnél. Harmadik lépés: Az eredő

I

áramot óvatosan 20-ról 30 amperesre növeljük. A normál állapotú kapcsolón nem folyhat számottevő áram (ez korlátot szab az áramváltoztatás ütemére), az összes áram gyakorlatilag a tekercsen folyik keresztül. Negyedik lépés: A szupravezető kapcsolót

r = 0

állapotba hozzuk (vagyis a tekercs áramát ,,befagyasztjuk''). Ötödik lépés:

I

-t nullára csökkentjük (ezt most gyorsan is megtehetjük, mert a kapcsoló szupravezető állapotban van). Mivel

I_{1}

nem változhat, az

r

-en átfolyó áram fog 30 A-t csökkenni. Utolsó lépés: Kikapcsoljuk a

K

főkapcsolót. A kívánt változást megvalósító folyamat a 14. ábrán látható.
3. feladat. Korongok ütközése felületi súrlódással
Egy

A

jelű,

m

tömegű,

R_{A}

sugarú, tömör, homogén korong

V

sebességű transzlációs (azaz forgás nélküli) súrlódásmentes mozgást végez a sima vízszintes

x - y

síkban,

x

irányban,

b

távolságban az

x

tengelytől. Összeütközik egy

B

jelű, kezdetben nyugvó, ugyancsak

m

tömegű, azonos vastagságú, de

R_{B}

sugarú, tömör, homogén koronggal, amely kezdetben a koordináta-rendszer origójában áll (15. ábra). Feltehetjük, hogy az érintkező felületek ütközés alatti súrlódása következtében az érintkezési pontban a korongok sebességének érintő irányú összetevője az ütközés után egyenlő lesz. Azt is feltehetjük, hogy a korongok középpontját összekötő egyenes mentén a korongok relatív sebességének nagysága az ütközés előtt és az ütközés után megegyezik.

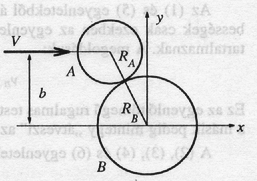15. ábra

1. Határozd meg az ilyen ütközés esetén a két korong ütközés utáni sebességeinek

x

és

y

komponenseit, azaz

V'_{A x}; V'_{A y}; V'_{B x}; V'_{B y}

értékét

m

R_{A}

R_{B}

V

és

b

ismeretében!
2. Határozd meg az

A

korong ütközés utáni

E'_{A}

és a

B

korong ütközés utáni

E'_{B}

mozgási energiáját

m

R_{A}

R_{B}

V

és

b

ismeretében!

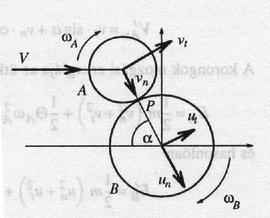16. ábra

Megoldás. Az ütközés során (amely nyilván csak akkor következik be, ha

b < R_{A} + R_{B}

), megmarad a rendszer

x

, illetve

y

irányú impulzusa (lendülete), vagy ami ezzel egyenértékű: a

P

ütközési pontban húzott érintő irányú (tangenciális), valamint az arra merőleges sugár irányú (normális) impulzuskomponensekre is felírhatunk megmaradási törvényt. A 16. ábra jelöléseivel

\begin{matrix} m V cos α & = m (u_{n} + v_{n}) & (1) \\ m V sin α & = m (u_{t} + v_{t}) & (2) \end{matrix}

Igaz továbbá, hogy a

P

pontra vonatkoztatva külön ‐ külön megmarad a két korong perdülete, hiszen az ütközés során fellépő erőknek nincs forgatónyomatéka erre a pontra. Vegyük figyelembe, hogy a perdület a tömegközéppont haladó mozgásából származó impulzusnyomatékból és a tömegközéppont körüli forgás

Θ ω

sajátperdületéből tehető össze:

\begin{matrix} m R_{A} \cdot V sin α & = m R_{A} v_{t} + Θ_{A} ω_{A}, & (3) \\ 0 & = m R_{B} u_{t} - Θ_{B} ω_{B}, & (4) \end{matrix}

ahol

Θ_{A} = m R_{A}^{2} / 2

, illetve

Θ_{B} = m R_{B}^{2} / 2

. Ezek a megmaradási tételek 4 egyenletet adtak, de az ismeretlenek száma 6 (

2 + 2

sebességkomponens és 2 szögsebesség). (A mechanikai energia megmaradása most nem teljesül, hiszen az ütközés rugalmatlan.) A hiányzó két egyenletet a relatív sebességekre megadott megszorítások szolgáltatják. (Ezek lényegében azt fejezik ki, hogy az ütközés sugár irányban tökéletesen rugalmas, érintő irányban pedig tökéletesen rugalmatlan. Kérdéses, hogy léteznek-e olyan kiterjedt testek, melyek ütközése ─ legalább jó közelítéssel ─ így írható le.)

\begin{matrix} V cos α = u_{n} - v_{n}, & (5) \\ v_{t} - R_{A} ω_{A} = u_{t} + R_{B} ω_{B} . & (6) \end{matrix}

Az (1) és (5) egyenletekből álló rendszer önmagában zárt, a normális irányú sebességek csak ezekben az egyenletekben fordulnak elő, más ismeretlent viszont nem tartalmaznak. A megoldásuk:

\begin{matrix} v_{n} = 0, u_{n} = V cos α . \end{matrix}

Ez az egyenlő tömegű rugalmas testek ütközésének jól ismert esete: az egyik test megáll, a másik pedig mintegy ,,átveszi'' az eredetileg mozgó test sebességét.
A (2), (3), (4) és (6) egyenletekből álló rendszer megoldása:

\begin{matrix} v_{t} & = \frac{5}{6} V sin α \\ u_{t} & = \frac{1}{6} V sin α \\ R_{A} ω_{A} & = R_{B} ω_{B} = \frac{1}{3} V sin α . \end{matrix}

Ezek ismeretében valamennyi keresett sebességkomponens könnyen számítható:

\begin{matrix} V'_{A x} = v_{t} \cdot sin α + v_{n} \cdot cos α = \frac{5}{6} V sin^{2} α = \frac{5 V b^{2}}{6 {(R_{A} + R_{B})}^{2}} stb. \end{matrix}

A korongok mozgási energiája az ütközés után:

\begin{matrix} E'_{A} = \frac{1}{2} m (v_{n}^{2} + v_{t}^{2}) + \frac{1}{2} Θ_{A} ω_{A}^{2} = \frac{1}{2} m V^{2} \cdot \frac{27}{36} sin^{2} α = \frac{1}{2} m V^{2} \cdot \frac{3 b^{2}}{4 {(R_{A} + R_{B})}^{2}}, \end{matrix}

és hasonlóan

\begin{matrix} E'_{B} & = \frac{1}{2} m (u_{n}^{2} + u_{t}^{2}) + \frac{1}{2} Θ_{B} ω_{A}^{2} = \frac{1}{2} m V^{2} \cdot (1 - \frac{11}{12} sin^{2} α) \\ = \frac{1}{2} m V^{2} \cdot (1 - \frac{11 b^{2}}{12 {(R_{A} + R_{B})}^{2}}) . \end{matrix}

Kísérleti verseny^{$^{*}$}

1. feladat. Egy áltátszó dielektrikum felület fényvisszaverő-képességének meghatározása.
Kísérleti berendezés:
1. He‐Ne lézer (kb.

\sim 1,5 mW

). A lézerből kijövő fény önmagában nem polarizált.
2. Két polárszűrő, amelyek fokbeosztású skálával vannak ellátva, az egyik (az

A

jelű polarizátor) a lézer előtt helyezkedik el, míg a másikat szükség esetén rajzszögek segítségével a rajztábla megfelelő helyére rögzítheted.
3. Két fényintenzitás-mérő detektor, amelyek fotocellából és mikroampermérőből állnak.
4. Fénynyaláb-osztó kör alakú üveglemez.
5. Átlátszó dielektrikum lemez (a továbbiakban minta). Ennek a mintának a fényvisszaverő-képességét és törésmutatóját kell meghatároznod.
6. Mintatartó állvány félkör alakú szögmérére erősítve, mozgatható karral.
7. Rajzszögek.
8. Rés és ernyő a lézernyaláb vízszintes belállítására és az optikai elemek beszabályozására.
9. Gyurma, amely az optikai elemek finom rögzítésére szolgál.
10. Fa rajztábla.
11. Milliméterpapírok.
Kísérleti feladatok:
1. Határozd meg a minta

R

reflexióképességét (fényvisszaverő-képességét) a fénysugár beesési szögének függvényében a p-komponensre vonatkoztatva. (A

p

-komponens a lézerfény azon összetevője, amelyben az elektromos tér párhuzamos a beesési síkkal.)
a) Határozd meg (

p

-komponens mérés segítségével), hogy az (

A

) polarizátor áteresztési iránya hány fokos szöget zár be a polarizátoron lévő jelzéshez képest! (Az áteresztési irány az átmenő fény elektromos térerősség vektorának rezgési irányát jelenti.)
b) Válaszd az egyik fényintenzitás-mérő detektort, és igazold alkalmas méréssel, hogy a fény intenzitása egyenesen arányos a mikroampermérő jelével. Rajzold le vázlatosan a mérésekhez használt optikai elrendezést! A mérési adataidat, továbbá az azokból számított értékeket (a számítási formulával együtt) foglald táblázatba! Abrázold a lineáris kapcsolatot grafikusan!
c) Határozd meg a minta fényvisszaverő-képességét a beesési szög függvényében a p-komponensre vonatkoztatva! Rajzold le vázlatosan az optikai elrendezést! Mérési adataidat, továbbá a számított fényvisszaverési képességet (a számítási formulával együtt) foglald táblázatba! Ábrázold a fényvisszaverő-képességet a beesési szög függvényében!
2. Határozd meg a minta törésmutatóját a lehető legpontosabban!
Útmutatás:
1. Ne nézz közvetlenül a lézerfénybe!
2. A lézersugár kimenő fényteljesítménye időben változhat! A kilépő fény intenzitásának változását állandóan követned kell a mérés alatt, és a kísérleti eredményeidet ennek figyelembevételével korrigálnod (helyesbítened) kell!
3. A lézernek állandóan működnie kell! Még a kísérlet befejezése után, a terem elhagyásakor sem szabad kikapcsolnod a lézert!
4. A visszavert fény egy bizonyos

Θ_{B}

beesési szögnél teljesen lineárisan polárossá válik. Erre a szögre a

tg Θ_{B} = n

összefüggés érvényes, ahol

n

a törésmutató.
Megoldás. 1. a) az útmutatás szerint egy bizonyos szögnél, az ún.

Θ_{B}

Brewster-szögnél a visszavert fény teljesen polárossá válik. Visszaverő felületként az ismeretlen törésmutatójú mintát választva, annak elforgatásával, illetve a mintára eső lézerfény útjába tett polárszűrő egyidejű forgatásával elérhetjük, hogy a visszavert fény intenzitása nulla legyen (a fénymérő detektor nem jelez). Ennél az elrendezésnél (17. ábra) a polárszűrő csak a

p

-komponenst engedi át. Az adott esetben az

Θ_{B} = 56, 3^{\circ}

-os szögnél és a polarizátor

ψ = 140, 5^{\circ}

-os állásánál következett be.
b) A nyalábosztó segítségével a 18. ábrán látható módon a lézerfényt két részre oszthatjuk. Ha a

P_{1}

polárszűrő rögzített állása mellett a

P_{2}

polárszűrőt

φ

szöggel elforgatjuk, a

D_{2}

detektorba jutó fény intenzitása az

\begin{matrix} I (φ) = I_{0} cos^{2} φ \end{matrix}

függvény szerint változik (ez az

I_{fény} \sim E^{2}

, és

| E_{szűrt} | = | E | \cdot cos φ

összefüggések következménye). Amennyiben a fénymérő detektor

I

árama arányos a detektorra eső fényintenzitással, így az

I_{áram} \sim I_{fény} \sim cos^{2} φ

lineáris kapcsolatnak kell teljesülnie, feltéve, hogy a mérés közben a lézer teljesítmény nem változott. Ha ez utóbbi bekövetkezne, a

D_{1}

detektor árama is megváltozik, s a változás mértékéből korrigálni lehet az adatokat. A mérések szerint jó közelítéssel lineáris a kapcsolat a fénymérő árama és a ráéső fény intenzitása között.

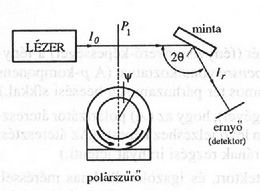17. ábra

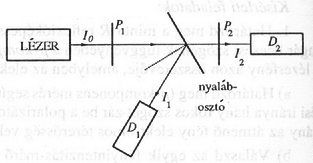18. ábra

c) Az előző alkérdésben igaznak bizonyult linearitás ismeretében különböző beesési szögeknél (

5^{\circ}

-tól

85^{\circ}

-ig) mérni lehet a visszavert fény relatív intenzitását (a lézer ingadozásait figyelembe véve és korrekciós faktorral helyesbítve).
2. A legkisebb visszaverőképesség (gyakorlatilag nulla) az említett Brewster-szögnél tapasztalható, ennek mért értéke

Θ_{B} = 56, 3^{\circ} \pm 0, 5^{\circ}

. Mivel az anyag

n

törésmutatója éppen

tg Θ_{B}

-vel egyenlő, innen

n = 1,50 \pm 0,02

adódik.
A mérési adatokat a 19. ábra mutatja.

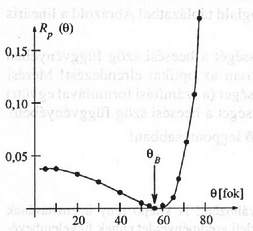19. ábra. A

p

-komponensre vonatkoztatott reflexió-képesség a beesési szög függvényében

Aki ismeri azt az összefüggést, hogy merőleges beesésnél (bármilyen polarizációjú fényre) a fényvisszaverőképesség:

\begin{matrix} R (Θ = 0) = \frac{n - 1}{n + 1}, \end{matrix}

ebből ─ a mérési adatokat a technikai okokból megvalósíthatatlan

0^{\circ}

-os esetre extrapolálva ─ az

R (0) \approx 0,028

adatból a törésmutatóra az

n = 1,48 \pm 0,04

értéket kapta.
2. feladat. Fekete doboz
Adott egy ,,fekete doboz'', amelyen két egyforma kivezetés van. A fekete dobozban legfeljebb 3 passzív elem található. Határozd meg a kivezetések közötti áramkörben lévő elemek adatait! A dobozt nem szabad kinyitni!
Kísérleti berendezés:
1. Kétsugaras oszcilloszkóp, továbbá egy mellékelt magyarázat a készüléken lévő gombokról.
2. Hangfrekvenciás jelgenerátor, továbbá egy mellékelt magyarázat a készüléken lévő gombokról.
3. 100 ohm (

\leq \pm 0,5 %

) értékre beállított ellenállásdoboz.
4. Csatlakozó-vezetékek.
5. A koaxiális kábelek. A fekete színjelzésű vezetékek a koax-csatlakozónál földeltek.
6. Különböző (lineáris-, log-, és log‐log) milliméter-papírok.
Megjegyzés: Azok a gombok, amelyek nincsenek feltüntetve a műszermagyarázatokon, a helyes állásba vannak beállítva. Ezekhez ne nyúlj!
Kísérleti feladatok:
1. Rajzold le az általad összeállított áramkört!
2. Add meg az általad mért és számított adatokat táblázatos alakban! A kapott eredményeket ábrázold megfelelően választott milliméter-papíron. (Jelöld be, hogy mit ábrázolsz a grafikonon és a tengelyeken is jelöld a mennyiségeket mértékegységükkel együtt!)
3. Rajzold le a fekete dobozban lévő áramkört, és add meg az áramköri elemek nevét és adatait! (Írd le, hogy milyen formulák alapján számoltál!)
Megoldás. 1. A 20. ábrán látható kapcsolásban az

R

ellenálláson eső

U_{R}

feszültség mérésével meghatározhatjuk a fekete dobozon áthaladó áramot, az ellenállásból és a fekete dobozon együttesen eső

U_{Z + R}

méréséből pedig következtethetünk a dobozhon eső feszültségre. Mindkét mennyiséget a kétsugaras oszcilloszkópon egyszerre mérhetjük, a jelgenerátoron a beállított

f

frekvencia függvényében. (

U_{R}

és

U_{Z}

mérése nem célszerű, mert akkor a

B

pont lenne az oszcilloszkóp viszonyítási pontja, nem pedig a közös ,,földelés'', s emiatt a hálózati 50 Hz zavaró hatása lényegesen erősebb lenne; gyakorlatilag mindig ,,brummot'' látnánk az oszcilloszkópon a mérendő jel helyett!)
2. A mérési adatokat, pontosabban a

Z + R

impedanciának a frekvenciafüggését a 21. ábrán tüntettük fel, log‐log skálát használva. Látható, hogy nagy frekvencián pedig

Z \sim 1 / f

(a meredekség

- 1

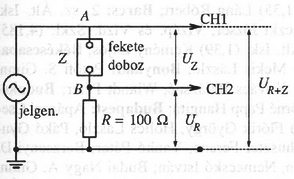20. ábra

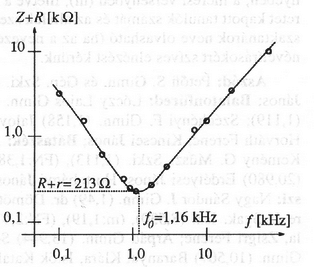21. ábra

3. A mérési adatok arra utalnak, hogy a fekete dobozban sorosan kapcsolt tekercs, kondenzátor és ellenállás található. A rezonancia-frekvenciánál,

f_{0} = 1,16 kHz

-nél az eredő impedancia 213

Ω

, innen

r = 113 Ω

. Nagy frekvencián

Z_{C} \approx 0

Z \approx L ω = L \cdot 2 π f

, alacsony frekvencián pedig

Z \approx 1 / (2 π f C)

. A kétsugaras oszcilloszkóp segítségével a két feszültség fáziskülönbsége is mérhető, s ennek ismeretében az

R

ellenállás ismert értéke is figyelembe vehető. A mérési adatokból

C \approx 0,58 μ F

és

L \approx 31,8 mH

adódott. Valamennyi mért mennyiség hibája 10% körüli érték.

Gnädig Péter

^{$^{*}$}A rendelkezésre álló idő: 5 óra.

^{$^{*}$}A rendelkezésre álló idő: $2 \times 2,5$ óra.