Kezdőlap


Cím:	1993-94. Beszámoló a fizika OKTV-ről
Szerző(k):	Holics László
Füzet:	1994/november, 449. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A fizika OKTV-t három kategóriában rendezték meg. Az első, iskolai fordulón 1993. december 3-án 4047 tanuló vett részt. A második, ugyancsak írásbeli fordulóra 1994. februárjában 454 tanulót hívtak be, közülük kategóriánként 24‐24-en vehettek részt az áprilisi kísérleti fordulón, amelyet a szakközépiskolásoknak a JATE-n, a gimnazistáknak pedig Budapesten ez ELTE-n, illetve a BME-n rendeztek meg.
Az alábbiakban ismertetjük a verseny második fordulójának feladatait és azok megoldását, valamint röviden utalunk a kísérleti fordulóban szereplő problémákra is.

Az I. kategória (szakközépiskolások) feladatai

1. feladat. Analitikai mérleget sárgaréz súlyokkal használunk. Mekkora tömegű plexiből készült test mérésekor tapasztalunk legalább egy skálarész különbséget a két mérés között, ha az egyiket száraz, a másikat párás időben végezzük el? Mindkét alkalommal

23^{\circ} C

-os a szoba hőmérséklete és a légnyomás

10^{5} Pa

. Párás időben a levegőben lévő vízgöz nyomása

2 \cdot 10^{3} Pa

. A mérleg érzékenysége

0,1 mg / skr

. (

ϱ_{Cu} = 8,5 \cdot 10^{3} kg / m^{3}; ϱ_{Plexi} = 1,18 \cdot 10^{3} kg / m^{3}

(Hilbert Margit)

Megoldás. A mérősúlyok súlya azért különbözik, mert a párás, illetve a száraz levegő sűrűségének különbsége miatt eltérő a súlyokra ható felhajtóerő. Legyen

M_{s}

a mérősúly tömege,

ϱ

a levegő,

ϱ_{P}

a plexi,

ϱ_{Cu}

a réz sűrűsége,

m

pedig a plexi keresett tömege. Az egyenlőkarúnak feltételezett mérleg egyensúlyára:

\begin{matrix} M_{s} g - \frac{M_{s}}{ϱ_{Cu}} ϱ g = m g - \frac{m}{ϱ_{P}} ϱ g . \end{matrix}

Innen

\begin{matrix} M_{s} = m \frac{ϱ_{Cu}}{ϱ_{P}} \frac{ϱ_{P} - ϱ}{ϱ_{Cu} - ϱ} . \end{matrix}

A párás és a száraz levegőbeli mérés alapján a két tömeg látszólagos különbsége:

\begin{matrix} Δ M_{s} = M_{s}' - M_{s} = m \frac{ϱ_{Cu}}{ϱ_{P}} \cdot (\frac{ϱ_{P} - ϱ_{2}}{ϱ_{Cu} - ϱ_{2}} - \frac{ϱ_{P} - ϱ_{1}}{ϱ_{Cu} - ϱ_{1}}) \approx m \frac{(ϱ_{Cu} - ϱ_{P}) (ϱ_{1} - ϱ_{2})}{ϱ_{P} ϱ_{Cu}}, \end{matrix}

ahol

ϱ_{1}

, illetve

ϱ_{2}

a száraz, illetve a nedves levegő sűrűsége, a különbségük pedig (a parciális nyomások törvénye szerint) megegyezik a

p = 2 \cdot 10^{3} Pa

nyomású és

T = 296 K

hőmérsékletű száraz levegő és vízgőz sűrűségének különbségével. Mivel

\begin{matrix} p V = \frac{m}{M} R T, vagyis ϱ = \frac{p M}{R T}, \end{matrix}

így

\begin{matrix} ϱ_{1} - ϱ_{2} = \frac{p}{R T} [M_{lev} - M_{H_{2} O}] = 8,94 \cdot 10^{- 3} kg / m^{3} . \end{matrix}

Ezzel a plexi keresett tömege:

\begin{matrix} m = Δ M_{s} \frac{ϱ_{P} ϱ_{Cu}}{(ϱ_{Cu} - ϱ_{P}) (ϱ_{1} - ϱ_{2})} = 15,3 g . \end{matrix}

(

Δ M_{s}

-t a mérleg 1 skálarésznyi érzékenységnek megfelelő 0,1 mg tömeggel azonosítottuk.)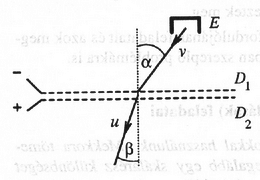

1. ábra

2. feladat. Finom szövésű, párhuzamos helyzetű

D_{1}

‐

D_{2}

dróthálók közé

U

feszültséget kapcsolnak az ábra szerinti polaritással. Az

E

elektronforrásból elektronok érkeznek

v

sebességgel a

D_{1}

hálóhoz.
a) Mutassuk meg, hogy az áthaladó elektronok

α

beesési és

β

törési szögére érvényes a Snellius‐Descartes törvény, azaz a

sin α / sin β

hányados független a beesési szögtől, minden elektronra ugyanaz az érték!
b) Határozzuk meg a törésmutató értékét!
(Feltehető, hogy a hálók között homogén elektromos mező van, máshol az elektromos térerősség zérus.

v = 3 \cdot 10^{6} m / s, U = 25 V

(Szegedi Ervin)

Megoldás. A hálók között csak a hálókra merőleges erő hat a részecskékre, tehát az elektronok sebességének a háló síkjával párhuzamos komponense nem változik meg:

\begin{matrix} v sin α = u sin β, \end{matrix}

(

u

az elektronok sebessége az irányváltoztatás után). A munkatétel szerint:

\begin{matrix} \frac{1}{2} m u^{2} - \frac{1}{2} m v^{2} = e U . \end{matrix}

A fenti két egyenletből ─ némi átalakítás után ─ adódik, hogy

\begin{matrix} \frac{sin α}{sin β} = \sqrt[]{1 + \frac{2 e U}{m v^{2}}} . \end{matrix}

Látható, hogy teljesül a Snellius‐Descartes-törvény. A törésmutató a megadott számadatokkal, illetve az elektronra vonatkozó táblázatbeli állandókkal

n = 1,42

-nek ad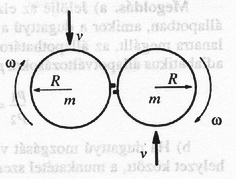ódik.

2. ábra

3. feladat. Légpárnás asztalon az ábra szerint két, azonos körüljárással,

ω = 2 s^{- 1}

szögsebességgel forgó

R = 4 cm

sugarú korong

v = 10 cm / s

sebességgel halad ellentétes irányban. A korongok a peremükön lévő elhanyagolható méretű tüskék mentén összeütköznek.
Határozzuk meg az ütközések utáni sebességeket, ha a korongok
a) tökéletesen rugalmatlan ütközések után mereven összetapadtak,
b) tökéletesen rugalmas, pillanatszerű ütközés után elválnak!

(Jurisits József)

Megoldás. a) A korongok az inerciarendszerben nyugvó érintkezési pont körül

ω_{1}

szögsebességgel merev testként együtt fognak forogni. A perdületmegmaradás tétele szerint (a Steiner-tételt is alkalmazva)

\begin{matrix} 2 (m v R - \frac{1}{2} m R^{2} ω) = 2 (\frac{1}{2} m R^{2} + m R^{2}) ω_{1} . \end{matrix}

Innen a keresett szögsebesség:

ω_{1} = 1 s^{- 1}

; a forgás az eresetivel ellentétes irányú.
b) A lendület megmaradása szerint a két korong az ütközés után csak egyenlő (

v_{1}

) nagyságú, ellentétes irányú sebességgel haladhat. A szimmetriából következik, hogy a korongok szögsebessége is azonos körüljárású, egyenlő (

ω_{1}

) nagyságú kell legyen az ütközés után. A perdületmegmaradás törvénye szerint

\begin{matrix} 2 (m v R - \frac{1}{2} m R^{2} ω) = 2 (m v_{1} R - \frac{1}{2} m R^{2} ω_{1}), \end{matrix}

a mechanikai energia (rugalmas ütközésnél érvényes) megmaradási törvénye alapján pedig

\begin{matrix} 2 (\frac{1}{2} m v^{2} + \frac{1}{4} m R^{2} ω^{2}) = 2 (\frac{1}{2} m v_{1}^{2} + \frac{1}{4} m R^{2} ω_{1}^{2}) . \end{matrix}

Az adatokat behelyettesítve és az egyenletrendszert megoldva

v_{1} = - 2 cm / s

, illetve

ω_{1} = - 4 s^{- 1}

adódik. Eszerint mind a sebesség, mind pedig a szögsebesség iránya megfordul az ütközés során.

A II. és III. kategória (valamennyi gimnazista) feladatai

1. feladat. Hőszigetelő falú, vízszintes tengelyű hengerben egy

m

tömegű dugattyú a külső légnyomásnál nagyobb nyomású levegőt zár el. Ha a dugattyú rögzítését megszüntetjük, akkor a dugattyú súrlódás nélkül mozog a hengerben. A létrejövő adiabatikus állapotváltozás során az elzárt gáz legnagyobb térfogata az eredetinek kétszerese. Határozzuk meg
a) a gáz legkisebb és legnagyobb nyomásának arányát,
b) a kezdeti nyomás nagyságát!
(A külső levegő nyomása

p_{k} = 10^{5} Pa

, a levegő tekinthető 5 szabadsági fokú gáznak, ezért a kétféle fajhőjének hányadosa

ϰ = c_{p} / c_{v} = 1,4

(Szegedi Ervin)

Megoldás. a) Jelölje az elzárt gáz kezdeti állapothatározóit

p_{1}, V_{1}, T_{1}

. Abban az állapotban, amikor a dugattyú a legjobban eltávolodott a kezdeti helyzetétől, s egy pillanatra megállt, az állapothatározók legyenek:

p_{2}, V_{2}, T_{2}

. Mivel

V_{2} = 2 V_{1}

, továbbá az adiabatikus állapotváltozásokra

p V^{ϰ} =

állandó, a nyomások aránya:

\begin{matrix} \frac{p_{1}}{p_{2}} = {(\frac{V_{2}}{V_{1}})}^{ϰ} = 2^{ϰ} = 2^{2,14} = 2,64. \end{matrix}

b) Ha dugattyú mozgását vizsgáljuk a két szélső (vagyis mzogási energia nélküli) helyzet között, a mukatétel szerint felírhatjuk, hogy

\begin{matrix} W_{külső} + W_{gáz} = 0. \end{matrix}

A külső levegő által végzett munka (

Δ V = V_{1}

felhasználásával):

\begin{matrix} W_{külső} = - p_{k} Δ V = - p_{k} V_{1} . \end{matrix}

Mivel a folyamat adiabatikus, a hőtan I. főtétele szerint (mivel

Q = 0

)

\begin{matrix} W_{gáz} = - Δ E_{gáz} = (\frac{f}{2}) (p_{1} V_{1} - p_{2} V_{2}) . \end{matrix}

Ezzel a munkatétel:

\begin{matrix} (\frac{f}{2}) (p_{1} V_{1} - p_{2} V_{2}) - p_{k} V_{1} = 0. \end{matrix}

Innen, a korábban kapott eredményt is felhasználva a kezdeti nyomás:

p_{1} = 1,65 \cdot 10^{5} Pa

.
2. feladat. A

d = 100 m

széles folyó két partját parabolaív hosszmetszetű híd köti össze. A pálya legmagasabb pontja

h = 5 m

magasan van a partok szintje felett. A hídon egy

m = 1000 kg

tömegű gépkocsi halad keresztül állandó

v = 20 m / s

nagyságú sebességgel. Mekkora erővel nyomja a kocsi a hidat
a) a híd legmagasabb pontján,
b) a két part közötti távolság 3/4 részében?
(A légellenállástól tekintsünk el! Számoljunk

g = 10 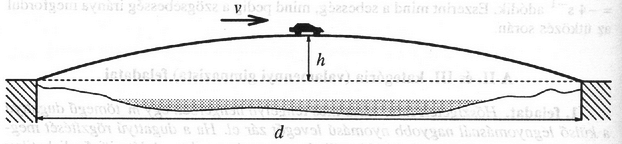m / s^{2}

-tel!)

3. ábra

(Holics László)

Megoldás. a) A gépkocsi mozgásegyenlete

\begin{matrix} m g - K = m \frac{v^{2}}{ϱ}, \end{matrix}

ahol

K

a híd által kifejtett kényszererő (ennek nagysága megegyezik a keresett, hidat nyomó erővel),

ϱ

pedig a pálya adott pontjához tartozó görbületi sugár. A feladat lényege ennek a görbületi sugárnak a meghatározása.
Bármilyen alakú pályán

v

pillanatnyi sebességgel mozgó testre igaz, hogy a sebességére merőleges (normális irányú) gyorsulása:

\begin{matrix} a_{n} = \frac{v^{2}}{ϱ} . \end{matrix}

Ha sikerül találnunk egy olyan mozgást, amelynek során a test az adott pályagörbe mentén halad, s ismerjük a normális irányú gyorsulást valamekkora pillanatnyi sebesség esetén, akkor a fenti összefüggésből kiszámíthatjuk a kérdéses ponthoz tartozó görbületi sugarat. Parabola esetében ez a mozgás egy alkalmas

v_{0}

kezdősebességgel, megfelelő

α

szögben eldobott kő ferde hajítása lehet. Ismerve a hajítás távolságát (a híd

d

fesztávolságát), és a

h

emelkedési magasságot, felírhatjuk a

\begin{matrix} d = \frac{2 v_{0}^{2} sin α cos α}{g} \end{matrix}

és a

\begin{matrix} h = \frac{v_{0}^{2} sin^{2} α}{2 g} \end{matrix}

összefüggéseket. Ezek hányadosából

tg α = 4 h / d = 0,2

, tehát

α = 11, 3^{\circ}

adódik, a vízszintes irányú sebesség pedig a szóbanforgó adatokkal

v_{x} = 50 m / s

. Mivel a pálya legfelső pontjában a kő sebessége vízszintes, így a pályára merőleges gyorsulása megegyezik magával a gyorsulással (ami mindvégig

g

). Innen a pálya görbületi sugara

ϱ = v_{x}^{2} / g = 250 m

. Mivel ez a mennyiség a pályagörbe alakjára jellemző szám (tehát független az adott pályán történő mozgás jellegétől), felhasználható az eredeti probléma, a hídon mozgó autó esetében is. A keresett nyomóerő:

\begin{matrix} K = h (g - \frac{v_{autó}^{2}}{ϱ}) = 8400 N . \end{matrix}

b) Az előbbiekhez hasonló módon számítható ki a parabola alakú pálya tetszőleges pontjához tartozó görbületi sugár, s abból a hídra ható nyomóerő. A híd (vízszintesen mért) 3/4 részénél például ez a sugár kb. 254 m-nek adódik, a hídra kifejtett erő pedig kb. 8430 N. Ez utóbbi erőnek a hídra merőleges (tehát normális irányú) összetevője 8370 N, az érintő irányú súrlódási erő pedig kb. 1000 N.
Az itt leírtakhoz hasonló ,,fizikai gondolatmenettel'' elemi úton meg lehet határozni egy szinuszgörbe tetszőleges pontjában a görbületi sugarat (lásd az FN. 2767. feladat megoldását a KöMaL 1994. évi 4. számában), vagy pl. az egymásra merőleges harmonikus rezgőmozgások ismert gyorsulásából egy ellipszis görbületét.
3. feladat. Egy

a = 10 {mm}^{2}

keresztmetszetű,

μ = 200

relatív permeabilitású vashuzalra szigetelt rézvezetékből

N = 2000

menetet sűrűn felcsévélünk, és ezt az egyrétegű tekercset

R = 10 cm

sugarú kör köré hajlítjuk. Az így kapott körtekercsben

I_{1} = 10 A

erősségű áramot indítunk, amelyet

Δ t = 1 s

alatt egyenletesen

I_{1} = - 10 A

erősségűre változtatunk. Mekkora és milyen irányú a gyorsulása az adott pillanatban a kör középpontjában lévő, a kör síkjában mozgó

v = 100 m / s

sebességű elektronnak akkor, amikor
a) az áram erőssége a tekercsben éppen zérus,
b) az áram csökkenésének kezdetétől

t_{1} = 60 s

telt el?

(Holics László)

Megoldás. A mozgó elektronra mind a mágneses, mind az elektromos mező erőt fejt ki. Meg kell vizsgálni, hogy a kérdéses pillanatokban milyen mezők vannak a kör középpontjában, és hogy az ezeket jellemző térerősség- és indukcióvektorok milyen irányúak.
Amikor nincs mágneses tér (

I_{a} = 0

), akkor csak a mágneses fluxusváltozás hoz létre (időben állandó) elektromos teret, amely

F = e E

erővel gyorsítja az elektront (függetlenül annak sebességállapotától). Amikor újra folyik áram a tekercsben (pl. a

t_{1} = 0,6 s

időpillanatban), a kör középpontjában mágneses mező is keletkezik, amely

F = e v \times E

erővel hat az elektronra.
a) Amikor az áram erőssége zérus, csak elektromos mező van jelen. A vékony vashuzal belsejében ún. toroidális mágneses mező alakul ki, amelynek fluxuserőssége a teljes keresztmetszet mentén állandónak vehető (hiszen a vashuzal 3,6 mm átmérője sokkal kisebb, mint a kör

R = 200 mm

sugara.) Ez a vékony mágneses fluxuscső az elektromos mező keltésében olyan szerepet játszik, mint a mágneses mező keltésénél a vékony áramjárta huzal: az áramjárta vezető mágneses terének analógiájára az (időben változó) mágneses fluxuselem keltette elektromos mező a Biot‐Savart-törvénynek megfelelő törvénnyel írható le. Mindössze annyit kell meghatároznunk, hogy mi felel meg egymásnak a kétféle folyamatban. Egyenes vezetőnél egy indukcióvonalra

\begin{matrix} B \cdot 2 r π = μ_{0} I \to B = \frac{μ_{0} I}{2 π r}, \end{matrix}

egyenes vékony tekercseknél

\begin{matrix} E \cdot 2 r π = - \frac{Δ Φ}{Δ t} \to E = - \frac{I}{2 π r} \frac{Δ Φ}{Δ t} . \end{matrix}

Innen látható, hogy a Biot‐Savart-törvényben szereplő

μ_{0} I

mennyiségnek

\frac{Δ Φ}{Δ t}

felel meg. Ezzel a kétféle ,,Biot‐Savart-törvény'':

\begin{matrix} Δ B = \frac{μ_{0}}{4 π} \frac{I Δ l}{r^{2}} sin α, illetve Δ E = \frac{1}{4 π} \frac{Δ Φ}{Δ t} \frac{Δ l}{r^{2}} sin α . \end{matrix}

A kör középpontjában az eredő elektromos térerősség az ismert összegzéssel határozható meg:

\begin{matrix} E = \sum Δ E = \sum \frac{1}{4 π} \frac{Δ Φ}{Δ t} \frac{Δ l}{r^{2}} sin α = \frac{1}{4 π} \frac{Δ Φ}{Δ t} \frac{1}{r^{2}} sin 90^{\circ} \sum Δ l, \end{matrix}

ahol

\sum Δ l = 2 r π

a kör kerülete. Innen a kör középpontjában a keresett térerősség:

\begin{matrix} E = \frac{1}{2 r} \frac{Δ Φ}{Δ t}, \end{matrix}

ami a feladat feltételei szerint időben állandó.
Az a) esetben a kérdezett pillanatban

B = 0

, de

\frac{Δ Φ}{Δ t} \neq 0

, sem a toroidtekercsen kívül, sem pedig a tekercs belsejében. (A lágyvashuzal hiszterézise elhanyagolható, ezért ha van is visszamaradó mágnesség a kérdezett pillanatban, a remanans mágnességnek az elektromos mezőt meghatározó változási üteme igen jó közelítéssel megegyezik az első mágnesezési görbe zérus gerjesztéshez tartozó változási ütemével, ami arányos az áramerősség változási gyorsaságával.)
A vashuzalbeli mágneses fluxus változása:

\begin{matrix} Δ Φ = Δ B \cdot A = μ_{0} μ_{r} \frac{Δ I N}{2 R π} \cdot A . \end{matrix}

Ezt a Boit‐Savart-törvénnyel analóg törvénybe helyettesítve megkapjuk az elektron gyorsulását:

\begin{matrix} a_{E} = \frac{e E}{m} \approx 1,41 \cdot 10^{8} m / s^{2}, \end{matrix}

iránya merőleges a kör síkjára.
b) A

t_{1} = 0,6 s

pillanatban a rézvezetékben

I_{1} = 2 A

erősságú áram folyik, és ez az áram mágneses mezőt kelt. Ez az áram ─ noha a körtekercsben folyik ─, éppen olyan mágneses mezőt hoz létre a toroid középkörének középpontjában, mint amilyet egyetlen menetnyi vékony, a középkör mentén folyó körvezető keltene, ha benne ugyanakkora áram folyna, mind a körtekercsben. Ez a mágneses mező

B_{1} = μ_{0} I_{1} / (2 R)

nagyságú, iránya merőleges a kör síkjára, így az általa létrehozott

\begin{matrix} a_{M} = \frac{1}{m} F_{Lorentz} = \frac{e}{m} v μ_{0} \frac{I_{1}}{2 R} \approx 2,21 \cdot 10^{8} m / s^{s} \end{matrix}

nagyságú gyorsulás

B

-re és

v

-re merőleges, tehát a kör síkjában fekszik. Az eredő gyorsulás nagysága

\begin{matrix} a = \sqrt[]{a_{E}^{2} + a_{M}^{2}} \approx 2,62 \cdot 10^{8} m / s^{2}, \end{matrix}

iránya pedig

\begin{matrix} φ = arctg \frac{a_{M}}{a_{E}} = 57, 7^{\circ} \end{matrix}

szöget zár be a tengellyel.
Megjegyzés. Egyesek arra gondolhatnak, hogy a tekercs belsejét kitöltő vashuzalban (szintén vezető lévén) a körülfogott fluxus változása miatt a tekercsbeli árammal ellentétes körüljárású áram indul, ami csökkenti a tekercs mágneses terét. Ha a vashuzalt nemcsak körré hajlítjuk, hanem a huzal végeit össze is forrasztjuk, akkor valóban kapunk egy körvezetőt, ami körülveszi az (inhomogén eloszlású) mágneses fluxust. Ebben a vezetékben azonban ─ a toroid középköre mentén mérhető maximális indukcióval számolt homogén fluxus esetén is ─ legfeljebb ezredakkora áram folyik, mint a rézvezetékben, s ennek megfelelően az általa keltett mágneses mező is elhanyagolhatóan kicsi.

A kísérleti forduló feladatai

A szakközépiskolások, akik Szegeden, a József Attila Tudományegyetemen versenyeztek, azt a feladatot kapták, hogy egy 1 mm-es rés, valamint diffrakciós rács felhasználásával állítsanak össze egy kézi spektroszkópot, kalibrálják a skálájába, majd különböző fényforrások (izzólámpa, kompakt fénycső, neoncső) fényét vizsgálva végezzenek színképelemző méréseket vele.
A szakközépiskolások másik feladata az volt, hogy egy 5 kivezetésű, csak ohmikus ellenállásokat tartalmazó fekete doboz belsejére következtessenek ampermérő, telep és dekádos ellenállásdoboz felhasználásával.
A gimnazisták közül a II. kategóriások Budapesten, az ELTE Általános Fizikai Tanszékén egy Siemens fényelem karakterisztikáját mérték, elektromos tulajdonságait tanulmányozták.
Idén először vett részt a verseny kísérleti fordulójának megrendezésében a Budapesti Műszaki Egyetem Fizikai Intézete. A III. kategóriás gimnazisták azt a feladatot kapták, hogy állapítsák meg, mekkora sebességgel áramlik a víz a laborban található (és természetesen zárt) csővezetékben. Ehhez különböző mérőeszközök álltak a versenyzők rendelkezésére. A korábban megszokott gyakorlattól eltérően a verseny kétlépcsős volt. Először a mérés elvileg lehetséges megvalósításáról, az ahhoz szükséges eszközökről és az alkalmazható mérési módszerekről kellett egy rövid tervet készítsenek a versenyzők. Ezt bizonyos idő múlva beadták (de annak másolata náluk maradt), majd a mérés tényleges elvégzéséhez további információkat, tanácsokat kaptak a szervezőktől.

A verseny végeredménye
A fizika I. kategória eredménye

I. díj: Kovács Krisztián (Békéscsaba, Kemény Gábor Műsz. Szki., III. o. t., tanárai: Mekis László, Varga István); II. díj: Birszki Bálint (Vác, Boronkay György Műsz. Középisk., IV. o. t., tanára: Arany-Tóth László); III. díj: Kumli Tamás (Pécs, Zipernovsky K. Ip. Szki., IV. o. t., tanárai: Kiss Jenő, Kardos Gyula); 4. Nagy Gábor (Bp., Kolos R. Műsz. Szki., IV. o. t., tanára: Szabó Erzsébet); 5. Korpos Tibor (Paks, Energetikai Szakképz. Int., tanárai: Csajági Sándor, Kotek László); 6. Tarsoly András (Zalaegerszeg, Ganz Á. Műsz. Középisk., IV. o. t., tanára: Sörlei József).
További helyezettek: 7. Takács Norbert (Győr, Pattantyús-Á. G. I. Szki., IV. o. t.); 8. Antos József (Bp., Egressy G. Ip. Szki., IV. o. t.); 9. Straub Kornél (Miskolc, Bláthy O. Villamosip. Szki., IV. o. t.); 10. Nyéki József (Debrecen, Gábor D. Elektr. Műsz. Középisk., III. o. t.); 11. Horváth Gabriella (Vác, Boronkay Gy. Műsz. Szki., IV. o. t.); 12. Benkó Tibor (Budapest, Egressy G. Ip. Szki., IV. o. t.); 13. Kiss Olivér (Debrecen, Mechwart A. Gépip. Műsz. Középisk., III. o. t.); 14. Csorba Zoltán (Békéscsaba, Széchenyi I. Közg. és Külker. Szki., IV. o. t.); 15. Krüpl Zsolt (Esztergom, Bottyán J. Műsz. Középisk., IV. o. t.); 16. Gazdag Károly (Barcs, Erdészeti-, Vízép. és Vízgazd. Szki., IV. o. t.).

A fizika II. kategória eredménye

I. díj: Szeredi Tibor (Budapest, Fazekas M. Főv. Gyak. Gimn., IV. o. t., tanára: Horváth Gábor); II. díj: Németh Tibor (Győr, Révai M. Gimn., III. o. t., tanára: dr. Somogyi Sándor); III. díj: Futó Gábor (Budapest, Fazekas M. Főv. Gyak. Gimn., IV. o. t., tanára: Horváth Gábor); 4. Juhász Sándor (Budapest, Fazekas M. Főv. Gyak. Gimn., IV. o. t., tanára: Horváth Gábor); 5. Költl Péter (Győr, Révai M. Gimn., IV. o. t., tanára: Székely László); 6. Kautny Szabolcs (Budapest, Arany J. Gimn., III. o. t., tanára: Seltsam László); 7. Jurek Zoltán (Debrecen, Fazekas M. Gimn., IV. o. t., tanára: Türk Zsuzsanna); 8. Wágner Ferenc (Tata, Eötvös J. Gimn., III. o. t., tanára: Ádám Árpád); 9. Csikor Ferenc (Budapest, Piarista Gimn., IV. o. t., tanára: Nyeste Pál); 10. Lengyel Krisztián (Cegléd, Kossuth L. Gimn., III. o. t., tanára: Tűri László).
További helyezettek: 11. Szép János (Szolnok, Verseghy F. Gimn., IV. o. t.); 12. Tóth Zoltán (Zalaegerszeg, Zrínyi M. Gimn., IV. o. t.); 13. Pálfalvi László (Pécs, Apáczai Cs. J. Gimn., IV. o. t.); 14. Buronyi László (Budapest, Fazekas M. Főv. Gyak. Gimn., III. o. t.); 15. Gálfi Gergely (Budapest, Budapesti Ref. Gimn., IV. o. t.); 16. Vidéki András (Kecskemént, Piarista Gimn., III. o. t.); 17. Szalai Zoltán (Győr, Kazinczy F. Gimn., IV. o. t.); 18. Kárpáti Attila (Budapest, Fazekas M. Főv. Gyak. Gimn., IV. o. t.); 19. Mészáros Attila (Zalaegerszeg, Zrínyi M. Gimn., IV. o. t.); 20. Borsányi Szabolcs (Budapest, Piarista Gimn., III. o. t.); 21. Ujvári Tamás (Pécs, JPTE Babits M. Gyak. Gimn., III. o. t.); 22. Brunczel András (Salgótarján, Bolyai J. Gimn., IV. o. t.); 23. Salk Miklós (Pécs, JPTE Babits M. Gyak. Gimn., III. o. t.); 24. Gillemot László (Budapest, Fazekas M. Főv. Gyak. Gimn., III. o. t.); 25. Kapta Krisztián (Csenger, Ady E. Gimn., IV. o. t.).

A fizika III. kategória eredménye

I. díj: Varga Dezső (Miskolc, Földes F. Gimn., III. o. t., tanára: Szabó Kálmán); II. díj: Prohászka Zoltán (Budapest, Veres Pálné Gimn., IV. o. t., tanára: Oporné Fodor Mária); III. díj: Szancsik Endre (Budapest, ELTE Apáczai Cs. J. Gyak. Gimn., IV. o. t., tanára: Flórik György); 4. Németh Zoltán Ádám (Budapest, ELTE Apáczai Cs. J. Gyak. Gimn., IV. o. t., tanára: Holics László); 5. Weiner Mihály (Budapest, Berzsenyi D. Gimn., III. o. t., tanára: Istók Katalin); 6. Balázs Márton (Budapest, ELTE Apáczai Cs. J. Gyak. Gimn., IV. o. t., tanára: Zsigri Ferenc); 7. Boros László (Budapest, ELTE Apáczai Cs. J. Gyak. Gimn., IV. o. t., tanára: Holics László); 8. Készmárki István (Szeged, JATE Ságvári E. Gyak. Gimn., IV. o. t., tanárai: Homolya Ernő, Erdei Imre); 9. Szabó János Zoltán (Budapest, ELTE Apáczai Cs. J. Gyak. Gimn., III. o. t., tanára: Zsigri Ferenc); 10. Bakos Gáspár (Budapest, ELTE Apáczai Cs. J. Gyak. Gimn., IV. o. t., tanára: Flórik György); 11. Gergi Miklós (Jászberény, Lehel Vezér Gimn., IV. o. t., tanára: Oltvölgyi Béla);
További helyezettek: 12. Görbe Mihály (Kecskemét, Katona J. Gimn., III. o. t.); 13. Környei László (Győr, Czuczor G. Bencés Gimn., IV. o. t.); 14. Kenesei Péter (Budapest, ELTE Radnóti M. Gyak. Gimn., IV. o. t.); 15. Halbritter András (Győr, Czuczor G. Bencés Gimn., IV. o. t.); 16. Koniorczyk Mátyás (Budapest, ELTE Apáczai Cs. J. Gyak. Gimn., IV. o. t.); 17. Valenta Ferenc (Budapest, ELTE Apáczai Cs. J. Gyak. Gimn., III. o. t.); 18. Garabán György (Budapest, Petőfi S. Gimn., IV. o. t.); 19. Fekete Attila (Budapest, Fazekas M. Főv. Gyak. Gimn., IV. o. t.); 20. Kasza Tamás (Kecskemét, Katona J. Gimn., IV. o. t.); 21. Kovács Szabolcs (Bonyhád, Petőfi S. Evang. Gimn., IV. o. t.); 22. Hódossy Szabolcs (Budapest, Táncsics M. Gimn., IV. o. t.); 23. Földi Péter (Salgótarján, Bolyai J. Gimn., IV. o. t.); 24. Adorjáni Endre (Budapest, ELTE Radnóti M. Gyak. Gimn., IV. o. t.).

Holics László