Kezdőlap


Cím:	1993. Beszámoló az Eötvös-versenyről
Szerző(k):	Radnai Gyula
Füzet:	1994/április, 225. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1993. október 15-én tartotta 70. Eötvös versenyét Budapesten és 11 vidéki városban az abban az évben érettségizettek és a középiskolai tanulók részére. A versenyzők ‐ bármilyen segédeszköz felhasználásával ‐ 5 órai munkaidő alatt három fizikai feladatot oldhattak meg. A versenyben 271 tanuló adott be értékelhető dolgozatot. Ismertetjük a feladatokat, azok megoldását és a verseny eredményét.

1. Egyik végén átmenő, vízszintes tengely körül súrlódásmentesen foroghat egy hosszú vasrúd. A rúd másik vége a rúd hossztengelyére merőleges sík.
A rudat közel függőleges helyzetbe hozzuk, a felső végére kicsiny mágneskorongot illesztünk, majd elengedjük őket.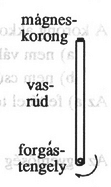

1. ábra

A korongra ható nehézségi erőnek legalább hányszorosa kell legyen a korong és a rúd között fellépő mágneses vonzerő, hogy a mozgás során a korong ne mozduljon el a rúdhoz képest?
A tapadási súrlódási együttható

μ_{0} = 1 / 6

(Varga István)

Megoldás. A feladat megoldásához a korongra és a rúdra felírt mozgásegyenleteket, valamint a munkatételt fogjuk felhasználni, miközben figyelembe vesszük a korong mozgására kirótt megkötéseket.
A 2. ábrán a korongra ható erőket tüntettük fel:

\vec{N}

az érintkezési felületre merőleges nyomóerő,

m \vec{g}

a nehézségi erő,

\vec{S}

a súrlódási erő,

\vec{F}

pedig a rúdirányú mágneses vonzóerő.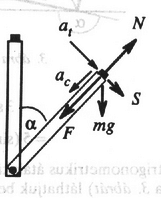

2. ábra

A korong mozgásegyenletei:

\begin{matrix} S + m g sin α = m a_{t}, \end{matrix}

\begin{matrix} F + m g cos α - N = m a_{c}, \end{matrix}

ahol

a_{t} = l β

az érintőleges (tangenciális) gyorsulás

a_{c} = l ω^{2}

a korong sugárirányú (centripetális) gyorsulása,

l

pedig a rúd hosszát jelöli.
A rendszer

β

szöggyorsulását és

ω

szögsebességét a forgómozgás dinamikai alapegyenletéből, illetve a munkatételből kaphatjuk meg. Tekintettel arra, hogy a kicsiny mágnes

m

tömege elhanyagolható a rúd

M

tömegéhez képest, elegendő a rúdra vonatkozó összefüggéseket felírni:

\begin{matrix} M g \frac{l}{2} sin α = \frac{1}{3} M L^{2} β, tehát β = \frac{3}{2} \frac{g}{l} sin α, \end{matrix}

\begin{matrix} \frac{1}{2} (\frac{1}{3} M l^{2}) ω^{2} = M g (\frac{l}{2} - \frac{l}{2} cos α), \end{matrix}

innen

\begin{matrix} ω^{2} = \frac{3 g}{l} (1 - cos α) . \end{matrix}

Ezekből az egyenletekből adódik, hogy

\begin{matrix} N = F + m g (4 cos α - 3), \end{matrix}

\begin{matrix} S = \frac{1}{2} m g sin α . \end{matrix}

A korong akkor nem mozdul el a rúdhoz képest, ha

a)	nem válik el a rúdtól; ennek feltétele: $N > 0$ ;

b)	nem csúszik meg; ennek feltétele: $\| S \| \leq ν_{0} N$

Az a) feltétel teljesül, ha

\begin{matrix} F > m g (3 - 4 cos α) \geq 7 m g . \end{matrix}

Az egyenlőség

α = π

-nél, vagyis a függőlegesen lefelé mutató rúdnál áll fenn.
A b) feltétel szerint

ν_{0} N = N / 6 \geq S

, ami

S

és

N

korábban kiszámított kifejezéseinek felhasználásával

\begin{matrix} \frac{F}{m g} \geq 3 + (3 sin α - 4 cos α) \end{matrix}

alakra hozható. A jobb oldalon a zárójelben álló kifejezés nem lehet nagyobb 5-nél és a maximális értéket

tg α_{0} = - 4 / 3

, azaz

α = α_{0} \approx 143^{\circ}

-nál éri el. Ezt az állítást a differenciálszámítás képletei segítségével, vagy a

\begin{matrix} 3 sin α - 4 cos α = 5 (\frac{3}{5} sin α - \frac{4}{5} cos α) = \\ = 5 (sin α_{0} sin α + cos α_{0} cos α) = 5 cos (α - α_{0}) \leq 5 \end{matrix}

trigonometrikus átalakítás felhasználásával, esetleg elemi geometriai módszerrel (lásd a 3. ábrát) láthatjuk be. A korong tehát akkor nem csúszik meg a rúdon, ha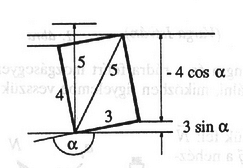

\begin{matrix} F \geq 8 m g . \end{matrix}

3. ábra

Látható, hogy a b)feltétel, vagyis a megcsúszást tiltó egyenlőtlenség az erősebb. Összefoglalva: a korong biztosan nem mozdul el a rúdhoz képes, ha a mágneses vonzóerő a korongra ható nehézségi erőnek legalább nyolcszorosa.
2.

U

alakú üvegcső mindkét szára 76 cm magas. A bal oldali szár zárt, a jobb oldali nyitott. A csőben higany helyezkedik el, a 4. ábrán látható módon. A higany egyensúlyban van, mert a bal oldali szárban a higany fölött egy kis levegő is van. A hőmérséklet 300 K, a külső légnyomás 76 Hgcm.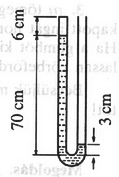

4. ábra

Lezárjuk a jobb oldali szárat, az egész berendezést 450 K-re melegítjük, majd visszahűtjük 300 K-re.
Ezek után hogyan fog elhelyezkedni a higany?

(Károlyházy Frigyes)

Megoldás. A jobb oldali szár lezárásakor a jobb oldali szárban a levegő nyomása

p_{1} = 76 H g c m

, az üvegcső alján tehát 79 Hgcm a higany nyomása, a bal oldali szárban levő levegő nyomása pedig

p_{2} = 79 H g c m - 70 H g c m = 9 H g c m

. A rendszert melegítve mindkét szárban levő levegő nyomása megnő. Ha valamilyen ok miatt a higany nem tudna elmozdulni, akkor a gáznyomások növekedése (izochor folyamatban) az eredeti nyomással egyenes arányban állna. Mivel

p_{1} > p_{2}

, a bal oldali szárban a nyomás növekedése nagyobb lenne, mint a jobb oldaliban, tehát a higany (amely természetesen el tud mozdulni), a melegítés során a jobb oldali szárban lesüllyed, a bal oldaliban pedig felemelkedik.
Amennyiben a higanyszint a jobb oldali szárban annyira lesüllyed, hogy eléri a kanyarulatot, akkor a további melegítés hatására a levegő egy része ,,átbugyborékol'' a bal oldali szárba. (A 4. ábra szerint a higany felszíne majdnem sík. Ez arra utal, hogy az üvegcső nem tekinthető kapillárisnak, a levegő nem képes a kanyarulatban is maga előtt ,,tolni'' a higanyszálat.)
Elvileg két lehetőség képzelhető el: a) Ha a rendszert ,,elegendően'' felmelegítjük, az átbugyborékolás biztosan bekövetkezik. Ilyenkor a berendezés visszahűtése után a bal oldali szárban több levegő lesz, mint kezdetben volt, tehát az eredeti hőmérsékleten a bal oldali levegőoszlop 6 cm-nél hosszabb lesz.
b) Ha a berendezést nem melegítjük fel annyira, hogy levegő bugyborékoljon át a kanyarulaton, akkor a visszahűtés után a rendszer minden részének valamennyi állapotjelzője megegyezik a kezdeti értékekkel, tehát a higany ugyanúgy fog elhelyezkedni, mint eredetileg.
A két lehetőség között a konkrét adatokkal elvégzett számolás dönt. Ha a levegő hőtágulását figyelembe vesszük, de az üvegnek és a higanynak a gázokhoz képest jóval kisebb hőtágulását elhanyagoljuk, akkor az adódik, hogy a 450 K-re való felmelegítés elegendő ahhoz, hogy levegő bugyborékoljon át a bal oldali szárba. A gáztörvényeket, illetve a higany egyensúlyi feltételét felírva azt kapjuk, hogy a jobb oldali higanyszint

T = 398,2 K

hőmérsékletnél eléri a kanyarulatot, bizonyos mennyiségű levegő átbugyborékol, majd a visszahűtés után a higanyszint a jobb oldalon az eredeti állapothoz képest 6,8 mm-rel magasabbra kerül.
Ha a higany és az üvegcső hőtágulását is figyelembe vesszük, akkor (a táblázatbeli hőtágulási együtthatókkal) az adódik, hogy a melegítés során a jobb oldali higanyszint csak 22 mm-t süllyed, tehát nem éri el a kanyarulatot! A rendszer lehűtése után tehát minden tekintetben visszaáll a kezdőállapot, a higanyszintek pontosan ott fognak megállapodni, ahol a felmelegítés előtt voltak.
(A Versenybizottság ‐ kellő indoklás esetén ‐ mindkét megoldást elfogadta.)
3.

m

tömegű,

Q

elektromos töltésű kicsiny gömböt fonálra függesztünk. Az így kapott ingát homogén, függőleges irányú,

B

indukciójú mágneses térbe helyezzük. Ha a gömböt kissé meglökjük, lengésbe jön. Azt tapasztaljuk, hogy a lengés síkja lassan körbefordul.
Becsüljük meg, hogy mennyi idő alatt tesz meg a lengés síkja egy teljes fordulatot!

(Tichy Géza)

Megoldás. A nyugalmi helyzetétől mért

\vec{r}

helyen lévő,

\vec{v}

sebességgel mozgó gömbre a fonálerő, a nehézségi erő és a mágneses tér okozta Lorentz-erő hat. Kicsiny kitérítés esetén a mozgás jó közelítéssel síkmozgásnak tekinthető. Az ingamozgásnál szokásos közelítéseket alkalmazva a fonálerőnek a mozgás (vízszintes) síkjába eső vetülete

- m ω^{2} \vec{r}

, ahol

ω

a fonálinga mágneses mező nélküli körfrekvenciája

(ω = \sqrt[]{g / l})

. A gömb mozgásegyenlete a mágneses mező jelenlétében:

\begin{matrix} m \vec{a} = Q \vec{v} \times \vec{B} - m \vec{r} ω^{2} . \end{matrix}

Ez az egyenlet az

\vec{r}

-re vonatkozó differenciálegyenlet, pontosabban: az

\vec{r}

vektor derékszögű komponensei között fennálló csatolt differenciálegyenlet-rendszer, melynek általános megoldása felsőbb matematikai ismereteket igényel.
A feladatot középiskolai szinten (tehát a differenciálegyenleteket matematikai elméletére való hivatkozás nélkül) is meg lehet oldani, ha felismerjük az (1) egyenlet és a közönséges síkinga forgó koordináta-rendszerből történő leírása (Foucault-inga, az Északi sarkon) közötti hasonlóságot. Ha egy

ω_{0}

körfrekvenciával jellemzhető síkinga kis amplitúdójú lengéseit egy olyan koordináta-rendszerből akarjuk leírni, amely

\vec{Ω}

szögsebességgel forog az inerciarendszerhez képest (

\vec{Ω}

függőleges vektor), akkor a következő (a Coriolis-erőt és a centrifugális erőt is figyelembe vevő) mozgásegyenletet kell tanulmányoznunk.

\begin{matrix} m \vec{a} = 2 m \vec{v} \times \vec{Ω} - m \vec{r} ω_{0}^{2} + m \vec{r} Ω^{2} . \end{matrix}

Ennek az egyenletnek a megoldását azonban ismerjük: mivel a lengés síkja az inerciarendszerben állandó, a forgó koordináta-rendszerhez képest

\vec{Ω}

szögsebességgel forog, tehát

T = 2 π / Ω

idő alatt tesz meg egy teljes fordulatot. Az (1) és (2) egyenleteket összehasonlítva láthatjuk, hogy

\vec{Ω} = Q \vec{B} / (2 m)

. (

ω_{0}

is kifejezhető a feladat többi paraméterével,)

\begin{matrix} ω_{0} = \sqrt[]{\frac{g}{l} + (\frac{Q B}{2 m})^{2},} \end{matrix}

de ez számunkra most érdektelen.) A lengési sík tehát a mágneses mező hatására

\begin{matrix} T = 4 π \frac{m}{Q B} \end{matrix}

idő alatt fordul teljesen körbe. (Érdekes, hogy a körülfordulás ideje csupán a kis gömb adataitól és a mágneses mező erősségétől függ, az inga lengési periódusidejétől viszont nem.)
Ha nem törekszünk ennyire pontos eredményre, hanem csak becslést akarunk adni a körülfordulás idejére (a feladat szövege is csak ezt igényli!), akkor elegendő a probléma közelítő megoldását megadni. A továbbiakban erre látunk három különböző példát.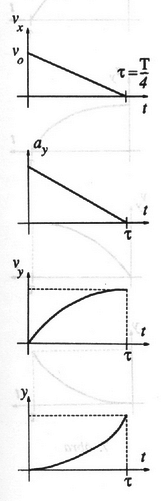

5. ábra

Első közelítésként tételezzük fel, hogy az

x

tengely irányában

v_{0}

sebességgel meglökött gömb (5. ábra)

v_{x}

sebessége egy negyed lengési periódus,

τ = T_{l e n g} / 4

idő alatt egyenletesen lassulva, az idő lineáris függvénye szerint változva csökken zérusra:

\begin{matrix} v_{x} (t) = v_{0} (1 - \frac{t}{τ}) . \end{matrix}

Ekkor a kezdősebességre merőleges (

y

irányú) gyorsulás is lineáris függvény

\begin{matrix} a_{y} (t) = \frac{Q v_{0} B}{m} (1 - \frac{t}{τ}), \end{matrix}

a megfelelő sebesség és elmozdulás pedig (a hatványfüggvényekre vonatkozó integrálási szabályokat alkalmazva):

\begin{matrix} v_{y} (t) = \frac{Q v_{0} B}{m} (t - \frac{t^{2}}{2 τ}), \end{matrix}

\begin{matrix} y (t) = \frac{Q v_{0} B}{m} (\frac{t^{2}}{2} - \frac{t^{3}}{6 τ}) . \end{matrix}

A maximális kitérés

x

irányban:

\begin{matrix} x_{m a x} = \frac{v_{0} τ}{2}, \end{matrix}

ezalatt

y

irányban a gömb elmozdulása

\begin{matrix} y_{m a x} = Q v_{0} B \frac{τ^{2}}{3 m} . \end{matrix}

(Vigyázat:

y_{m a x}

nem a legnagyobb elmodulás

y

irányban, hiszen

t = τ

pillanatban, amikor a test

x

irányú sebessége előjelet vált, a

y

irányú sebesség még nem csökkent le nullára, sőt, éppen maximális.) A lengési sík (kicsinynek feltételezett

φ

elfordulási szögére a

\begin{matrix} φ \approx tg φ = \frac{y_{m a x}}{x_{m a x}} \end{matrix}

becslés adható (6. ábra). A sík forgásának szögsebessége:

ω = φ / τ

, a körülfordulás ideje pedig

T_{1} = 3 π m / (Q B)

, ami a pontos érék 3/4 része.

6. ábra

Második közelítésben tegyük fel, hogy a gömb

v_{x}

sebessége koszinusz függvény szerint csökken nullára (7. ábra):

\begin{matrix} v_{x} (t) = v_{0} cos \frac{π}{2} \frac{t}{τ} . \end{matrix}

A rezgőmozgás ismert képleteit alkalmazva megfelelő elmozdulás

\begin{matrix} x (t) = \frac{2 v_{0} τ}{π} sin \frac{π}{2} \frac{t}{τ}, \end{matrix}

y

irányú gyorsulás, sebesség és elmozdulás pedig

\begin{matrix} a_{y} (t) = \frac{Q v_{0} B}{m} cos \frac{π}{2} \frac{t}{τ}, \end{matrix}

\begin{matrix} v_{y} (t) = \frac{Q v_{0} B}{m} \cdot \frac{2 τ}{π} sin \frac{π}{2} \frac{t}{τ}, \end{matrix}

\begin{matrix} y (t) = \frac{Q v_{0} B}{m} \cdot (\frac{2 τ}{π})^{2} \cdot (1 - cos \frac{π}{2} \frac{t}{τ}) . \end{matrix}

7. ábra

Az előző közelítésben alkalmazott gondolatmenetet követve kiszámítjuk a negyed periódus utáni

φ

szögelfordulást, ebből a szögsebességet, végül pedig a teljes körülfordulási időt, amire

T_{2} = π^{2} m / (Q B)

, a pontos érték

π / 4

-szerese adódik.
Harmadik közelítésünk az előzőktől lényegesen eltérő gondolatmenetre támaszkodik. Ne vizsgáljuk a lengés negyed periódusát, szorítkozzunk csak a meglökést követő igen rövid

△ t

időtartamra! A megfelelő irányú elmozdulások az egyenletes, illetve a rövid idő alatt állandónak tekinthető Lorentz-erőnek megfelelő egyenletesen változó mozgás képletei szerint

\begin{matrix} △ x = v_{0} △ t, \end{matrix}

\begin{matrix} △ y = \frac{Q v_{0} B}{2 m} {(△ t)}^{2} . \end{matrix}

A szögelfordulás nagysága ezalatt

\begin{matrix} △ φ = \frac{△ y}{△ x} = \frac{Q B}{2 m} △ t, \end{matrix}

a megfelelő szögsebesség

\begin{matrix} ω = \frac{△ φ}{△ t} = \frac{Q B}{2 m}, \end{matrix}

a lengési sík teljes körülfordulási ideje pedig

T_{3} = 4 π m / (Q B)

. Ez az idő pontosan egyenlő a helyes értékkel, ami nem véletlen, hiszen most ‐ az adott keretek között ‐ nem hanyagoltunk el semmi lényegeset. Ez a megoldás mégsem tekinthető a kérdéses mozgás teljes leírásának, hiszen nem bizonyítja, hogy a lengési sík elfordulásának szögsebessége időben állandó. Ha valahonnan tudjuk, hogy az elfordulás egyenletes, akkor annak ütemét meghatározhatjuk a mozgás kezdeti, nagyon rövid szakaszából, de ha ebből az értékből a mozgás későbbi menetére következtethetünk, az csak becslésnek tekinthető.

A verseny eredménye

I. díjat nyert a verseny 1. helyezettje: Katz Sándor, az ELTE fizikus hallgatója, aki Bonyhádon érettségizett a Petőfi Sándor Evangélikus Gimnáziumban, mint Erdélyesi János, Jurisits József és Kotek László tanítványa.
II. díjat nyert a verseny 2 ‐ 6. helyezettje: 2. Veres Gábor, az ELTE fizikus hallgatója, aki Balassagyarmaton érettségizett a Balassi Bálint Gimnáziumban, mint Bognár Mihályné és Fűrész István tanítványa. 3. Prohászka Zoltán, a budapesti Veres Pálné Gimnázium IV. osztályos tanulója, Oporné Fodor Mária tanítványa. 4. Gefferth András, a BME informatika szakos hallgatója, aki Budapesten érettségizett a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban, mint Horváth Gábor tanítványa. 5. Futó Gábor, a Fazekas Mihály Fővárosi Gyakorló Gimnáziujm IV. osztályos tanulója, Horváth Gábor tanítványa. 6. Burcsi Péter, a pápai Türr István Gimnázium és Óvónői Szakközépiskola II. osztályos tanulója, Németh Zsolt tanítványa.
III. díjat nyert a verseny 7-11. helyezettje: 7. Kovács Krisztián, a békéscsabai Kemény Gábor Műszaki Szakközépiskola III. osztályos tanulója, Mekis László tanítványa. 8. Varga Dezső, a miskolci Földes Ferenc Gimnázium III. osztályos tanulója, id. Szabó Kálmán tanítványa. 9. Székely Sándor, a BME informatikus szakos hallgatója, aki Kecskeméten érettségizett a Katona József Gimnáziumban, mint Németh Ágnes tanítványa. 10. Költl Péter, a győri Révai Miklós Gimnázium IV. osztályos tanulója, Székely László tanítványa. 11. Farkas Zénó, az ELTE fizikus hallgatója, aki Győrben érettségizett a Révai Miklós Gimnáziumban, mint Takács István tanítványa.
A bíráló bizottság (Radnai Gyula (elnök), Károlyházy Frigyes, Gnädig Péter) a beérkezett dolgozatok közül csak ezt a 11 dolgozatot díjazta, a többit nem rangsorolta. Az első díjjal 6000 Ft, a másodikkal 3000 Ft, a harmadikkal 2000 Ft pénzjutalom is járt az Eötvös Loránd Fizikai Társulat jóvoltából.
Gratulálunk a nyerteseknek!

Radnai Gyula