Kezdőlap


Cím:	Intellektuális Maraton `93
Szerző(k):	Rajkovits Zsuzsa
Füzet:	1994/április, 220. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A harmadik ,,Intellektuális Maraton'' elnevezésű komplex (matematika, fizika, angol) versenyt 1993. november 2. és 8. között rendezték meg Szentpétervárott.
Hazánkat ezúttal is az ELTE gyakorlóiskoláiból válogatott csapat: Vargha Márton (Trefort Ágoston Gimnázium), Németh Ádám (Apáczai Csere János Gimnázium), Kenesei Péter (Radnóti Miklós Gimnázium) képviselte. A versenyen diákjaink matematikából és fizikából írásbeli egyéni- és szóbeli csapatversenyben, angolból csak egyéni szóbeli megmérettetésben vettek részt. Az alábbiakban közöljük a verseny feladatait:

Matematika

1. Keressük meg az összes olyan négyjegyű négyzetszámot, amelyeknek első 2 számjegye egyenlő szám, és utolsó két számjegye is egyenlő.
2. El lehet-e helyezni az 1, 2,

...

, 81 számokat egy 9

\times

9-es négyzetrácsban úgy, hogy minden egyes vízszintes sorban a számok összege egyenlő legyen?
3. Az egységnyi oldalú

A B C D

négyzet

B C

és

C D

oldalain az

M

és

N

pont úgy helyezkedik el, hogy a

C M N

háromszög kerülete 2 egységnyi. Határozzuk meg az

M A N

szöget.
4. Oldjuk meg a következő egyenletet:

\begin{matrix} \sqrt[]{x_{1} - 1^{2}} + 2 \sqrt[]{x_{2} - 2^{2}} + ... + n \sqrt[]{x_{n} - n^{2}} = \frac{x_{1} + x_{2} + ... + x_{n}}{2} . \end{matrix}

5. Az

A B D

háromszögben az

A B D

szög 120

^{\circ}

. Az

A D

oldalon lévő

C

pont olyan tulajdonságú, hogy az

A B = C D = 1

, és az

A B C

szög 90

^{\circ}

. Határozzuk meg az

A C

oldal hosszát.
6. A Központi Bank 15, 20 és 48 rubeles címletű bankjegyeket bocsátott ki és kivonta a forgalomból az összes egyéb címletű pénzt.

a)	Bizonyítsuk be, hogy bármely összeget, amely egész szám, ki lehet fizetni ezekkel a bankjegyekkel, feltételezve, hogy kaphatunk visszajáró pénzt is, természetesen ugyanezekben a címletekben.

b)	Bizonyítsuk be, hogy egy bizonyos $N$ -től kezdve, bármely összeget visszajáró pénz nélkül is ki tudunk fizetni. Határozzuk meg a lehetséges legkisebb ilyen $N$ -t.

7. Bizonyítsuk be, hogy az 1 280 000 401 összetett szám.
8. Legyenek az

a_{1}, a_{2}, ..., a_{n}

számok egymástól különböző természetes számok. Bizonyítsuk be a következő egyenlőtlenséget:

\begin{matrix} \frac{a_{1}^{2} + a_{2}^{2} + ... + a_{n}^{2}}{a_{1} + a_{2} + ... + a_{n}} \geq \frac{1 +^{2} + 2^{2} + ... + n^{2}}{1 + 2 + ... + n} \end{matrix}

Fizika

1. Legfeljebb mekkora az a szög, amely alatt egy testet elhajlítva mozgása során mindig távolodik az eldobás helyétől. (Homogén gravitációs térben, a légellenállástól eltekintünk.)
2. Egy

m

tömegű test

l

hosszúságú fonálon függőleges, sima falon lóg. A felfüggesztési pont alatt, attól

x

távolságra szöget verünk a falba. Az ingát az egyensúlyi helyzetéből

π / 2

szöggel kitérítve elengedjük.

a)	Mekkora $x$ esetén mozog a test a szögben megakadt fonálon körpályán?

b)	Mekkora $x$ esetén halad el legalább egyszer a test a szög fölött?

3. Egy rakéta a második kozmikus sebességnél kisebb

v

sebességgel indul egy bolygóról. Lehetőség van arra, hogy egy segédhajtóművet rövid időre bekapcsoljunk; így esetleg a bolygó vonzását leküzdhetjük. (A bolygónak nincs légköre.) Mikor tegyük ezt meg:

a)	azonnal a főhajtómű kikapcsolása után

b)	amikor a rakéta sebessége nullává válik,

c)	mindegy, mert azok az erők, amelyek a rakéta és a kilövellt gáz között működnek, a rakéta ‐ gáz rendszert tekintve belső erők.

Indokoljuk a választ!
4. A felsorolt eszközök közül mi teszi lehetővé a szobában lévő molekulák kinetikus energiájának meghatározását?

a)	pszichrométer (nedvességmérő)

hőmérő,

c)	barométer.

A szoba térfogatát tekintsük ismertnek. (Mi is a szobában vagyunk.)
5. Ismeretes, hogy a háromdimenziós világunkban az elektromos töltések a vezetők felületén helyezkednek el. Igaz-e az állítás egy sík, kétdimenziós világban? Más szóval: a vezető határvonal mentén fognak-e elhelyezkedni a Coulomb-erővel kölcsönható részecskék?
6. Egy

C

kapacitású kondenzátornak

Q

töltést adunk, majd a

K_{1}

és

K_{2}

kapcsolókon keresztül, két egyforma

L

induktivitású tekercshez kötjük. Először a

K_{1}

kapcsolót zárjuk, majd amikor az első tekercsben az áramerősség értéke

I_{0}

, akkor a

K_{2}

-t is zárjuk.
Határozzuk meg:

a)	a tekercseken külön-külön az átfolyó áram maximális értékét,

b)	a kondenzátor maximális töltését.

Az egyéni- és csapateredményeket is tartalmazó összesített értékelésben 38 csapat mezőnyében tanulóink a 13. helyen végeztek. Az első helyet a moszkvai 57. számú Gimnázium szerezte meg. Angolból a magyar csapat a második lett.
A jövőben egy, az ország különböző helyeiről, hazai versenyek nyerteseiből válogatott csapatot is szeretnénk nevezni, amelynek eddig ─ a részvételi díj és az utazási költségek finanszírozása miatt ─ csupán anyagi akadálya volt.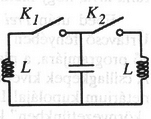

\begin{matrix} Rajkovits Zsuzsa \\ ELTE Általános Fizika Tanszék \end{matrix}