Cím: Az 1993-94. tanévi OKTV feladatai, eredményei
Füzet: 1994/november, 413 - 423. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatok megoldása és a részletes végeredmények megjelennek az Országos Közoktatási Szolgáltató Iroda Országos Középiskolai Tanulmányi Verseny Matematikából 1993/94. tanév című kiadványában. A kiadvány megrendelhető Lajos Józsefnétől (OKSZI, 1054, Budapest, Báthori u. 10.). Levélcím: 1399, Budapest, pf. 701/432.

I. KATEGÓRIA (A szakközépiskolák tanulói)
Első (iskolai) forduló

1. Oldjuk meg a pozitív számok halmazán a következő egyenletrendszert!
x+y+x+yx-y=240x-y,

x2+y2=353.

2. Az ABC háromszög A csúcsánál lévő belső szögének szögfelezője AD (D a BC oldalon van). Az ABD háromszög beírt körének középpontja azonos az ABC háromszög köré írt körének középpontjával.
Mekkorák az ABC háromszög szögei?
3. Egy vizsgán 20 kérdésre kellett válaszolni. Az értékeléskor minden jó válasz 5‐5 pontot ért, viszont minden rossz válasz esetén 2‐2 pontot levontak. Ha egy kérdésre a vizsgázó nem válaszolt, akkor arra 0 pontot kapott. Így valamelyik vizsgázó 48 pontot gyűjtött.
Hány jó választ adott?
4. Az ábrán szereplő ABCD és EFGH paralelogrammák területe egyenlő. Bizonyítsuk be, hogy CE párhuzamos FB-vel!
5. Bizonyítsuk be, hogy az an=3n2+3n+7 (n=1,2,3,...) képlettel definiált sorozat öt egymás után következő tagja között mindig van olyan tag, amelyik 5-tel osztható!
6. Legyen 0<x<2π. Igazoljuk, hogy
1-22≤sin2x+sinxcosx≤1+22.

Az x változó mely értékénél (értékeinél) áll fenn egyenlőség?
Második forduló

1. Oldjuk meg a következő egyenletet a valós számok halmazán:
logx26+log162(1x)+log1x(16)+log6x=-34.

2. Egy síkbeli konvex ötszög csúcsai legyenek az A1, A2, A3, A4, A5 pontok. Az A1A2, A2A3, A3A4, A4A5 szakaszok felezőpontjai rendre a B1, B2, B3, B4 pontok. Végül a B1B3 és a B2B4 szakaszok felezőpontja a C1, illetve a C2 pont. Milyen arányban metszik egymást az A1C2 és az A5C1 szakaszok?
3. Hány gyöke lehet az
|x2+6x+8|=x+p

egyenletnek?
Hogyan függ a gyökök száma a p paraméter értékétől?
4. Az ABCD konvex négyszöget az AC áltója két egyenlő területű háromszögre osztja. Az AC átlón felvett M (belső) ponton át az AB oldallal párhuzamosan húzott egyenes a BC oldalt a P pontban, az M ponton átmenő és a CD-vel párhuzamos egyenes az AD oldalt a Q pontban metszi.
a) Igazoljuk, hogy MPAB+MQCD=1.
b) Hogyan kell az M pontot megválsztani, hogy az MPC és az MQA háromszögek területeinek összege minimális legyen?
5. 1993 darab különböző valós szám közül bármelyik 997 darab számot kiválasztva és összeadva, a kapott összeg nagyobb a maradék 996 darab szám összegénél. Bizonyítsuk be, hogy ekkor az adott 1993 darab szám mindegyike pozitív!
Harmadik (döntő) forduló

1. Az x4-x3-14x2+2x+24=0 egyenletről tudjuk, hogy négy valós gyöke van, és két gyökének összege 0. Oldjuk meg az egyenletet!
2. Jelölje a téglatest felszínét A, testátlójának a hosszát d, továbbá legyen k≥2 tetszőleges valós szám.
Bizonyítsuk be, hogy
kd2-A

sohasem lehet negatív.
3. A síkbeli koordináta-rendszerben egy derékszögű háromszög csúcspontjai legyenek A(a;0), B(0;b), C(0;0), ahol a és b pozitív racionális számok. A háromszög N belső pontját válasszuk meg úgy, hogy
NCA∢=NAB∢=NBC∢

teljesüljön. Bizonyítsuk be, hogy az N pont koordinátái is racionális számok!
II. KATEGÓRIA
(Nem speciális matematika tantervű gimnáziumok tanulói)
Első (iskolai) forduló

1. Az ABC derékszögű háromszög AC befogója egy kocka élével, BC befogója pedig a kocka lapátlójával egyenlő hosszú. Bizonyítsuk be, hogy az ABC háromszögnek van két egymásra merőleges súlyvonala!
2. Adjuk meg azokat a pozitív egészekből álló (x;y) számpárokat, amelyek megoldásai a következő egyenletnek:
x2-4xy+5y2=25.

3. Oldjuk meg a valós számok halmazán a következő egyenletet
|1-x-2|⋅(x2+4x-3)=1.

4. Az AB körív F felezőpontján átmenő egyenes a körívet másodszor az F és B közötti M pontban metszi. Az F pontból az AM egyenesre állított merőleges talppontját jelölje K. Bizonyítsuk be, hogy AK=(AM+MB)/2.
5. Legyen Sn=1+2+3+...+n és
Pn=S2S2-1⋅S3S3-1⋅S4S4-1⋅...⋅SnSn-1.

Határozzuk meg azt a legkisebb n értékét, amelyre Pn>2,99.
Második forduló

1. Az ABC és A1B1C1 háromszögek oldalai: AB=c, BC=a, CA=b; A1B1=c1, B1C1=a1, C1A1=b1. Bizonyítsuk be, hogy az ABC és A1B1C1 háromszögek akkor és csakis akkor hasonlók, ha
aa1+bb1+cc1=(a+b+c)(a1+b2+c1).

2. a) Állítsik elő az 19931995 hatványt egynél több egymást követő pozitív páratlan szám összegeként.
b) Legalább hány tagú az ilyen összeg?
3. Adott az ABCD tetraéder. A tér egy P pontjának merőleges vetülete az AB egyenesen P1, a CD egyenesen P2. Határozzuk meg azoknak a P pontoknak a halmazát, amelyekre az
AP12+BP12+CP22+DP22

összeg minimális.
4. Milyen valós x értékekre teljesül a
x+3+6x-3=7x3-3x2-9x+276

egyenlőség?
Harmadik (döntő) forduló

1. Legyenek x1,x2,...,xn a [0;6] intervallum olyan számai, amelyekre teljesül a
P=x1x2...xn=(6-x1)2(6-x2)2...(6-xn)2

egyenlőség. Határozzuk meg P maximumát.
2. Egy téglatest alaplapja az ABCD, fedőlapja az A1B1C1D1 téglalap; AA1, BB1, CC1, DD1 párhuzamos élek. Az AB=c él hossza rögzített, az AD és AA1 élek hossza változhat. Az A csúcsot tartalmazó és a BD1 testátlóra merőleges γ sík a téglatestet két egyenlő térfogatú részre vágja szét. Legfeljebb mekkora lehet a γ által a téglatestből kimetszett sokszög területe?
3. Legyen N olyan 16-jegyű pozitív egész, amelynek jegyei között a 0, 1, 4, 9 nem fordul elő. Bizonyítsuk be, hogy N-nek van néhány olyan egymást követő számjegye, amelyek szorzata négyzetszám.
Igaz-e a feladat állítása a fenti típusú 15-jegyű számokra is?
III. KATEGÓRIA
(A gimnáziumok speciális matematika tantervű osztályainak tanulói)
Első (iskolai) forduló

1. Egy egység oldalú négyzetben két kör helyezkedik el, amelyeknek nincs közös belső pontja (egymást kívülről, ill. a négyzet határát belülről érinthetik). Mennyi a kerületük összegének a lehető legnagyobb értéke?
2. Hány olyan legfeljebb 10-jegyű pozitív egész szám van, amely osztható negyzetgyökének (alsó) egészrészével? (Pl. a 12 ilyen, mert ⌊12⌋=3 osztója a 12-nek, de a 22 nem ilyen, mert ⌊22⌋=4 nem osztója a 22-nek.)
3. Eszternek és Zsófinak 3‐3 forintja van. Egy szabályos érmével dobálnak, fej esetén Eszter kap Zsófitól 1 forintot, írás esetén pedig Zsófi kap Esztertől 1 forintot. Addig játszanak, amíg valamelyikük pénze elfogy. Mennyi a valószínűsége annak, hogy legalább 100 dobásra sor kerül?
4. Legyen f olyan nemkonstans valós együtthatós polinom, amellyel minden x,y valós számra
f(x)f(y)≤f2(x+y2)

teljesül. Mutassuk meg, hogy f-nek pontosan egy valós gyöke van.
5. Egy 1993 szögpontú teljes gráf minden élét színezzük úgy, hogy semelyik csúcsba sem fut két azonos színű él. Bizonyítsuk be, hogy ekkor van 17 olyan pont, amelyek közül bármelyik kettőt különböző színű él köt össze.
Második (döntő) forduló

1. Tekintsük az 1994 dimenziós vektorokat, azaz azokat az (a1,a2,...,a1994) szám-1994-eseket, ahol az ai ,,koordináták'' tetszőleges valós számok. Nevezzünk egy ilyen vektort ,,bumfordi''-nek, ha a koordinátái között legfeljebb két különböző érték fordul elő (azaz például minden koordinátája -1 vagy 2). Legkevesebb hány bumfordi vektor összegeként állítható elő az (1,2,...,1994)?
2. Egy egységnyi sugarú kört kívülről érintenek a k1, k2, k3, k4, k5 és k6 körök (az érintési pontok ebben a sorrendben követik egymást az egységkörvonalon), továbbá ki és ki+1 egymást is érintik kívülről (i=1,2,3,4,5). A ki kör sugara ri (i=1,2,3,4,5,6). Mutassuk meg, hogy ha ri+2=ri+1/ri (i=1,2,3,4) teljesül, akkor k1 és k6 is kívülről érintik egymást.
3. Egy tetszőleges m pozitív egészhez vegyünk minden lehetséges módon olyan a1<a2<...<at egészeket, amelyekre a1=m és az a1a2...at szorzat négyzetszám (t=1 is megengedett). Jelöljük S(m)-mel at lehető legkisebb értékét. Például S(1)=1, S(2)=6, mert m=2 esetén a 2⋅3⋅6 szorzat a legjobb választás, S(3)=8, S(4)=4 stb.
Bizonyítsuk be, hogy az S(2), S(3), S(4), ...sorozatban éppen a pozitív összetett számok szerepelnek, éspedig mindegyik pontosan egyszer fordul elő.
Az 1993‐94. évi matematika Országos Középiskolai Tanulmányi Vereseny eredményei

I. kategória
(A szakközépiskolák tanulói)

1. Halasi Zoltán, IV.o., Barcs, Erdészeti és Vízgazdálkodási Szki, tanára: Lőrincz Csabáne;
2. Nagy Gábor, IV.o., Budapest, Kolos Richárd Műszaki Szki, tanára: Karády Györgyné;
3. Szabadi Péter, II.o., Paks, Energetikai Szakképzési Intézet, tanára: Árokszállási Eszter, Árokszállási Tibor;
4. Antos József, IV.o., Budapest, Egressy Gábor Ipari Szki, tanára: Oros Lukácsné;
5. Krizsán Csaba, IV.o., Vác, Boronkay György Műszaki Középiskola, tanára: Benedek Ilona;
6. Novák András, III.o., Kecskemét, Kada Elek Közgazdasági Szki, tanára: Szenesné Durucz Anna;
7. Antal György, IV.o., Zalaegerszeg, Csány László Közgazdasági Szki, tanára: Kocsisné Molnár Margit;
8. Patócs Zoltán, IV.o., Pécs, Zipernowsky Károly Ipari Szki, tanára: Németh József;
9. Horváth Gabriella, IV.o., Vác, Boronkay György Műszaki Középiskola, tanára: Benedek Ilona;
10. Gál Marcell, III.o., Budapest, Trefort Ágoston Kéttannyelvű Műsz. Szki. és Gimnázium, tanára: Csapó Judit.
Miniszteri dicséretben részesültek:
11. Birszki Bálint, IV.o., Vác, Boronkay György Műszaki Középiskola; 12. Ádámku Miklós, IV.o., Budapest, Vásárhelyi Pál Kereskedelmi Szki; 13. Fődi Zoltán, IV.o., Kecskemét, Kada Elek Közgazdasági Szki; 14. Tar Zoltán, IV.o., Debrecen, Gábor Dénes Elektronikai Műszaki Középiskola; 15. Pletyák Attila, IV.o., Nyíregyháza, Széchenyi István Közgazdasági Szki; 16. Kovács Krisztián, III.o., Békéscsaba, Kemény Gábor Műszaki Szki; 17. Puskás József, IV.o., Debrecen, Gábor Dénes Elektronikai Műszaki Középiskola; 18. Eisenberger Aranka, IV.o., Paks, Energetikai Szakképzési Intézet; 19. Hirdi László, III.o., Pécs, Radnóti Miklós Közgazdasági Szki; 20. Zsihovszki Krisztián, IV.o., Eger, Neumann János Közgazdasági Szki és Gimnázium; 21. Meidlinger Nikoletta, IV.o., Győr, Baross Gábor Közgazdasági Szki; 22. Palócz Béla, IV.o., Szeged, Kőrösy József Közgazdasági és Külkereskedelmi Szki; 23. Veres Zoltán, IV.o., Kazincbarcika, Irinyi János Műszaki Szki; 24. Mészáros Róbert, IV.o., Kecskemét, Kada Elek Közgazdasági Szki; 25. Bogos Zsuzsa, III.o., Szigetszentmiklós, Batthyány Kázmér Gimnázium és Szki; 26. Bitera Krisztián, IV.o., Győr, Jedlik Ányos Gépipari Szki; 27. Benkó Tibor, IV.o., Budapest, Egressy Gábor Ipari Szki; 28. Mikáczó Zsolt, IV.o., Budapest, Újpesti Műszaki Szki; 29. Pelhős Bálint, IV.o., Nagykanizsa, Cserháti Sándor Mezőgazdasági és Gépészeti Szki; 30. Hartai Zoltán, III.o., Kazincbarcika, Irinyi János Műszaki Szki.
Megyei dicséretben részesült 26 tanuló.
II. kategória
(Nem speciális tantervű gimnáziumok tanulói)

1. Prohászha Zoltán, IV.o., Budapest, Veres Pálné Gimn., tanára: Erdőssy Jenőné;
2. Döbrente Gábor, IV.o., Budapest, Városmajori Gimn., tanára: Hadas Ildikó;
3. Izsák Ferenc, III.o., Szombathely, Nagy Lajos Gimn., tanárai: Rozmán Gyula, Peresztegi László;
4. Környei László, IV.o., Győr, Czuczor Gergely Bencés Gimn., tanára: Csonka László;
5. Visy Balázs, IV.o., Budapest, Fazekas M. Főv. Gyak. Gimn., tanára: Hámori Veronika;
6. Bettesch Gábor, IV.o., Paks, Vak Bottyán Gimn., tanára: Dr. Müller János;
7. Bajszi István, IV.o., Bonyhád, Petőfi Sándor Evangélikus Gimn., tanára: Katz Sándor;
8. Király Tamás, IV.o., Budapest, Kölcsey Ferenc Gimn., tanára: Bíró Józsefné;
9. Surányi Gábor, III.o., Budapest, Fazekas M. Főv. Gyak. Gimn., tanára: Nizsalovszky Ferenc;
10. Borbás Gergely, III.o., Miskolc, Herman Ottó Gimn., tanára: Demény Magdolna.
Miniszteri dicséretben részesültek:
11. Molnár Gábor, IV.o., Budapest, ELTE Apáczai Csere János Gyak. Isk.; 12. Szávai Gergely, III.o., Szolnok, Verseghy Ferenc Gimnázium; 13. Beer Gábor László, IV.o., Szombathely, Nagy Lajos Gimn.; 14. Kovács Szabolcs, IV.o., Bonyhád, Petőfi Sándor Evangélikus Gimn.; 15. Halbritter András, IV.o., Győr, Czuczor Gergely Bencés Gimn.; 16. Maróti Gábor, IV.o., Szombathely, Nagy Lajos Gimn.; 17. Kasza Tamás, IV.o., Kecskemét, Katona József Gimn.; 18. Kovács Gábor, III.o., Budapest, ELTE Radnóti M. Gyak. Isk.; 19. Heim László, III.o., Budapest, Kodály Zoltán Magyar Kórusiskola; 20. Mécs Ildikó, IV.o., Budapest, Eötvös József Gimn.; 21‐30. Bencsáth Boldizsár, III.o., Budapest, Budai Nagy Antal Gimn.; Égi József, IV.o., Bonyhád, Petőfi Sándor Evangélikus Gimn.; Farkas Bálint, IV.o., Budapest, ELTE Apáczai Csere J. Gyak. Isk.; Hegedüs Viktor, III.o., Paks, Vak Bottyán Gimn.; Hussami Péter, III.o., Budapest, ELTE Radnóti M. Gyak. Isk.; Lovassy Árpád, IV.o., Tata, Eötvös József Gimnázium; Insperger Tamás, IV.o., Hódmezővásárhely, Bethlen Gábor Gimn.; Mátrabérci Dávid, IV.o., Bonyhád, Petőfi Sándor Evangélikus Gimn.; Somlói Dániel, III.o., Budapest, Városmajori Gimn.; Szalmás Lajos, III.o., Hatvan, Bajza József Gimnázium.
Megyei dicséretben részesült 19 tanuló.
III. kategória
(A gimnáziumok speciális matematika tantervű osztályainak tanulói)

1. Koblinger Egmont, III.o., Budapest, Fazekas Mihály Főv. Gyak. Gimn., tanárai: Táborné Vincze Márta, Thiry Imréné;
és Szeidl Ádám, IV.o., Miskolc, Földes Ferenc Gimn., tanárai: Vass István, Veres Pál, Szabó Kálmán;
3. Szádeczky-Kardoss Szablocs, III.o., Budapest, Fazekas Mihály Főv. Gyak. Gimn., tanárai Táborné Vincze Márta, Thiry Imréné: ;
4. Csörnyei Marianna, IV.o., Budapest, Fazekas Mihály Főv. Gyak. Gimn., tanárai: Fazakas Tünde, Montágh Balázs, Babai László;
5. Madarassy Pál, IV.o., Budapest, Fazekas Mihály Főv. Gyak. Gimn., tanárai: Thiry Imréné, Vincze Márta, Horváth Gábor;
6. Váczi Péter, III.o., Szeged, Radnóti M. Kísérleti Gimn., tanárai: Mike János, Vincze István, Kosztolányi József;
7. Takács Orsolya, IV.o., Budapest, Szent István Gimn., tanára: Juhász István;
8. Párniczky Benedek, IV.o., Budapest, Fazekas Mihály Főv. Gyak. Gimn., tanárai: Montágh Balázs, Fazakas Tünde;
9. Kárpáti Attila, IV.o., Budapest, Fazekas Mihály Főv. Gyak. Gimn., tanárai: Thiry Imréné, Vincze Márta;
10. Szél Róbert, IV.o., Szeged, Radnóti M. Kísérleti Gimn., tanárai: Kosztolányi József, Vincze István.
Miniszteri dicséretben részesültek:
11. Marx Dániel, III.o., Budapest, Szent István Gimn.; 12. Hegedűs Gál, IV.o., Budapest, Fazekas Mihály Főv. Gyak. Gimn.; 13. Jurek Zoltán, IV.o., Debrecen, Fazekas Mihály Gimn.; 14. Juhász Sándor, III.o., Budapest, Fazekas Mihály Főv. Gyak. Gimn.; 15. Szeredi Tibor, IV.o., Budapest, Fazekas Mihály Főv, Gyak. Gimn.; 16. Németh Ákos, IV.o., Budapest, Fazekas Mihály Főv. Gyak. Gimn.; 17. György András, IV.o., Budapest, Árpád Gimn.; 18. Szörényi Balázs, IV.o., Szeged, Radnóti M. Kísérlet Gimn.; 19. Kotosz Balázs, IV.o., Szeged, Radnóti M. Kísérleti Gimn.; 20. Függ Róbert, IV.o., Szeged, Radnóti M. Kísérleti Gimn.; 21. Néz Péter, IV.o., Zalaegerszeg, Zrínyi Miklós Kísérleti Gimn.; 22. Nagy Katalin, III.o., Veszprém, Lovassy László Gimn.; 23. Bakcsi Gergely, IV.o., Budapest, Árpád Gimn.;
Megyei dicséretben részesült 24 tanuló.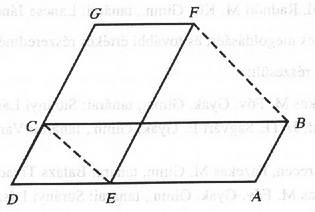