Cím: Mit lehet nyerni, ha egy kicsit engedünk a biztosból? 2. rész
Szerző(k):  Vancsó Ödön 
Füzet: 1994/április, 171 - 182. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1993/3. szám 104 ‐ 109. oldalán megjelent három probléma közül az első vizsgálata során jutottunk el az ún. Gauss-féle haranggörbéhez. Mivel ennek szerepe, mint a későbbiekben látni fogjuk, nemcsak a binomiális eloszlás közelítésekor jelentős, ezért szeretnénk megadni függvényként.
Próbáljuk meg az előzőekben ,,szemléletesen látott'' tényt analizálni, ami természetesen a matematikai analízis segítségével történik. Tehát írjuk föl, mit szeretnénk becsülni:

P(X=k)=(nk)⋅pk⋅(1-p)n-k=n!k!(n-k)!⋅pk⋅(1-p)n-k.
Ennek becsléséhez először a faktoriálisok nagyságáról kellene tudni valamit. Először A. Moivre-nak sikerült erre egy közelítő formulát találnia, amely 1730-ban jelent meg Miscellanea Analytica című művében. Ebben a könyvben szerepel még a következőkben előforduló normális eloszlással kapcsolatos fontos képlet:
∫0∞e-x2dx=12π,

illetve a komplex számokat ismerők számára nevezetes (cosα+sinα)n=cosnα+sinnα Moivre-féle képlet is. A sors játéka, hogy ez a faktoriálisokra vonatkozó képlet, amelyet néhány évvel később James Stirling is megadott, nem Moivre, hanem Stirling-formula néven vált ismertté: n!≈(ne)n⋅2πn, ahol két ,,csúnya'' szám is szerepel: az e és a π. Az utóbbit nyilván minden olvasó ismeri, az előbbit csak az analízisben járatosabbak, akik már sorozatok határértékvel foglalkoztak. Az e szám leggyakoribb definíciója:
limn→∞(1+1n)n=e.
A formula bizonyítását nem fogjuk ezen a helyen leírni, akit érdekel, elolvashatja (pl. [2]-ben 19-23. o.). Annyit mutatunk csak meg, hogy milyen induló ötlet kell hozzó. Nem n!-t hanem logn!-t fogjuk megbecsülni, mert akkor a szorzatból összeg lesz, ami sokkal kezelhetőbb. A ∑logn kifejezés, ahol log a természetes logaritmus, melynek alapja éppen a fent definiált ,,e'' szám, egy közelítő összege x→logx függvénygörbe alatti területnek. Így a fenti kifejezés a logx függvény integráljával becsülhető (lásd a 3. ábrát).
Ha tudjuk, hogy a logx egy primitív függvénye xlogx-x, akkor már majdnem megvan a keresett formula, hiszen az (ne)n tényező ebből adódik. A hiba becslése adja a másik tényezőt. Megjegyezzük, hogy már n>10 esetén is kisebb a hiba, mint 1% ( 10-nél 0,83%, 67-nél 0,12%), így nagy n-ekre jól lehet használni a becslést.
A továbbiakban ezt a formulát fogjuk használni az n! helyett:
n!k!(n-k)!⋅pk⋅(1-p)n-k=nn⋅n2π⋅k(n-k)⋅kk⋅(n-k)n-k⋅pk⋅(1-p)n-k.
Az egyszerűség kedvéért legyen p=1/2.
Ekkor
f(k)=P(X=k)=nn⋅n2π⋅k(n-k)⋅kk⋅(n-k)n-k⋅12n.
Most ha elvégezzük az I. rész 2. ábráin is használt transzformációt, mivel a csúcs n/2-ben van, s a binomiális eloszlás szórása σ=np(1-p), azaz n/2:
z=k-n/2n/2=2k-nn,
és
φn(z)=σ⋅f(k).
n→∞ esetén φn(z) tart a következő φ(z) függvényhez:
φ(z)=12π⋅1e-z2/2⋅(e-zez)z2=12π⋅e-z22.
(A levezetést ld. [3]-ban.) Ezt a függvényt hívják a standard normális eloszlás sűrűségfüggvényének. Ez egy folytonos függvény, nem lépcsős, mint a binomiális eloszlásé, amelyet ezzel közelítünk:
4. ábra
Hogyan lehet ezzel most ténylegesen közelítő számításokat végezni? Számunkra általában binomiális összegek kellenek, pl.
∑k≤xP(X=k)=∑k≤xn!k!(n-k)!⋅pk⋅(1-p)n-k.
Ha most a fenti közelítést akarjuk használni, akkor lévén, hogy folytonos függvényről van szó, a transzformációt elvégezve az Y=X-npnp(1-p) változó már standard normális eloszlású, azaz P(Y<z)=∫-∞z12πe-x2/2dx
Az analízisből ismeretes azonban, hogy a fenti integrál csak közelítéssel számolható ki, nincs analitikus képlettel felírható primitív függvénye az x→e-x2 függvénynek. Mivel nagyon gyakran használjuk ezt az integrált, van egy elfogadott jelölés: P(Y<z)=Φ(z)=∫-∞z12πe-x2/2dx. A Φ függvény értékeit táblázatban szokták megadni. Mivel φ szimmetrikus az origóra, ezért Φ(0)=0,5. Ebből a szimmetriából következik az is, hogy Φ(-z)=1-Φ(z). Ezzel lehet negatív érékekre is meghatározni Φ-t. (Lásd a 4. ábrát, és az 1. táblázatot.
Mivel a binomiális eloszlás lépcsős függvény, míg a normális eloszlás folytonos, jobb illeszkedést kapunk az ún. korrekciós formulával (lásd az 5. ábrát is):
P(X≤x)=P(Y≤x+0,5-npnp(1-p))=Φ(x+0,5-npnp(1-p))=Φ(x+0,5-μσ),P(X<x)=P(Y≤x-0,5-npnp(1-p))=Φ(x-0,5-npnp(1-p))=Φ(x-0,5-μσ),P(X>x)=1-Φ(x+0,5-npnp(1-p))=1-Φ(x+0,5-μσ),P(X≥x)=1-Φ(x-0,5-npnp(1-p))=1-Φ(x-0,5-μσ),

5. ábra

Ezek szerint lehet számolni a binomiális eloszlás közelítésével. Van még egy fontos kérdés, hogy milyen nagy n-re jó ez a közelítés. A helyzet bonyolult, mert ez p-től is függ. Van egy még Laplace-tól származó gyakorlati kritérium, miszerint, ha
np(1-p)>9,
akkor már legalább két tizedes pontossággal jó a közelítés, s természetesen ha np(1-p) sokkal nagyobb, mint 9, akkor a közelítés rendje is lényegesen javul. Ennek elemzése azonban meghaladja ennek a cikknek a kereteit, s nem is volt célunk ezt megtenni, mégis a használat feltételeit tisztázni kellett. A részleteket lásd pl. [3] 195-207. oldalig, vagy [4] 142-147. oldal.
Gyakorlásul nézzük meg, mi van, ha 10%-kal több megrendelést veszünk fel, hogy tele legyen a repülőgép. A 10% esetünkben 25 fő. Vajon mit lehet mondani, ha 275 megrendelést veszek föl, akkor milyen eséllyel fér be minden utazni szándékozó a gépbe? Esetünkben a várható érték np=275⋅0,9=247,5, míg a szórás np(1-p)=275⋅0,09=0,3275≈4,975.
Tehát Φ(250,5-247,54,975)=Φ(0,603)=0,7257, azaz kb.72% az esélye, hogy 275 megrendelést felvéve még nem kerülünk kellemetlen helyzetbe.
Ezután próbáljuk meg az eredeti kérdést megválaszolni, tehát nem a megrendelésszám ismert, hanem annak az esélyét kérdezzük, vajon nem lép-e fel a visszamondás egy bizonyos rögzített esélynél kisebb valószínűséggel. Már egy kicsit tájékozottabbak vagyunk, hiszen pl. 99%-ra rögzítjük az esélyt, akkor tudjuk, hogy 252 megrendelés még bőven jó, s a 275 meg már túl sok. Természetesen végigpróbálhatnánk a kettő között minden számot, s kiderülne, hol lépjük át 0,99-es küszöböt. Azonban éppen azért csináltuk végig a fenti közelítő számolást, hogy annak hasznát vegyük. Tehát a kérdésünk a következőképpen szól:
Legfeljebb milyen nagy n-ekre lehet 0,99 eséllyel 250-nél kisebb vagy egyenlő az utazók száma? Ha most az utazók számát normális eloszlással közelítjük, amelynek várható értéke μ=n⋅0,9, szórása σ=n⋅0,9⋅0,1=0,3n, akkor ehhez az kell, hogy az Y=X-0,9n0,3n új változó kisebb legyen, mint 250-0,9n0,3n legalább 99% eséllyel. Mivel az új változó standard normális eloszlású, azért látható az 1. táblázatból, hogy 2,33-nál már több, mint 99% eséllyel lesz kisebb a véletlen számunk, amely az utazók számát jelöli az n jelentkező közül.
Tehát 250-0,9n0,3n>2,33, vagyis 250-0,9n>0,699n. Mivel a bal oldal pozitív, azért 250-0,9n is az kell legyen, tehát n<277. Négyzetre emlve:
62500-450n+0,81n2>0,4886⇔81n2-45048,86n+6250000>0.
Ennek megoldása n<265,13 vagy n>291,03. Az utóbbit kizárja az n<277 kikötés, tehát n<265,13 vagyis mivel n egész, ezért n<265.
Ezzel választ adtunk a kérdésre, ha a biztonsági szint 99%-os, akkor legfeljebb 265 megrendelést vehetünk föl. Ezzel a várható utasszám 250⋅0,9=225-ről 265⋅0,9=238,5-re emelkedett.
Ez 13,5×30000=405000Ft bevétel növekedést jelent járatonként! S a ,,túlcsordulási'' rizikó csak 1%. Természetesen kiszámolható más rizikó faktorral is a feladat, ezt gyakorlásul ajánjuk az olvasónak.
Ha 5%-os a rizikó faktor, akkor hány megrendelés vehető föl, s mi a helyzet 0,1% esetén? Mekkora átlagos bevétel növekedést jelentenek járatonként a fenti esetek?
Látható, hogy a rizikó faktor és a bevétel növekedés egyirányú, ha csökkentem a rizikót, csökken a bevétel is. Ebben már a managementnek kell döntenie. Nyilván a visszamondás egy esetleges hosszú távú utast taszít át a konkurenciához, s így nem szabad gyakorinak lennie.
Végezetül ne felejtsük el, hogy a függetlenség fontos feltétel volt. Ha az egyes utasok nem függetlenek, akkor kell információ arról, hogyan függnek össze. Ha valaki csoportosan utazik pl. családdal, munkatársakkal, akkor gyakran a kiesése az egész csoport kiesését vonja maga után. Ekkor még többen esnek ki, vagyis az esélyeink a visszamondásnál nőnek, tehát becslésünk még inkább igaz lesz. Ha emiatt még több megrendelést akarunk felvenni, akkor ennek kalkulálásához további információ kell az együttes visszamondások számáról, gyakoriságáról. Ez egy lehetséges útja modellünk finomabbá tételének. Tudni kell azonban, hogy minden ilyen lépés, bár az eredmények egyre közelebb lesznek a valósághoz, növeli a matematikai nehézségeinket, amelyeket manapság leginkább a számítógépek segítségével lehet megoldani. Szimulációs és egyéb programokkal, vagy egyszerűen csak a sokmillió számítás elvégeztetésével. Nekünk azonban most csak az ismerkedés volt a célunk.
A második probléma tisztázásáhz idézzük fel, miről van szó:
2. Probléma: (ismerve a sokaság eloszlását, mit lehet mondani egy minta eloszlásáról, amelyet ebből a sokaságból vesznek?)
Egy, az Országos Rendőrfőkapitányság és a Főügyészség által közölt statisztikából tudjuk, hogy Magyarországon 1990-ben 341 061 bűncselekmény vált ismertté (feljelentés, eljárás indítás), s ebből 187 655 esetben az elkövető ismeretlen maradt. Ha most kiválasztunk 1000 bűncselekményt a 341 061-ből, akkor vajon mekkora eséllyel lesz legalább 400 esetben ismeretlen az elkövető? Mit kell érteni kiválasztáson? Hogyan lehet megvalósítani a kiválasztás ,,véletlenszerűségét'', amelyre a modellünk mond valamit?
Nagyon gyakori, hogy egy nagy sokaságról tudunk valamit, s arra vagyunk kíváncsiak, vajon hogyan tükröződik ez egy valahogyan kiválasztott jóval kisebb elemszámú mintában. Az alapvető kérdés persze éppen az lesz, hogy hogyan válasszuk ki ezt a mintahalmazt a teljes sokaságból, mint alaphalmazból. Azok a számítások, amelyeket majd elvégzünk, alapvetően arra támaszkodnak, hogy a mintahalmazt valamilyen módon ,,egyenletesen véletlenszerűen'' tudjuk kiválasztani, amin természetesen azt értjük, hogy semelyik elemnek sincs ,,prioritása'' a kiválasztási folyamat során. Ezt persze könnyebb kijelenti, mint megvalósítani. A legegyszerűbb eset, s természetesen egy bevezető példában ezt választottuk, amikor egyetlen egy tulajdonság fennállása szerint csoportosítjuk a sokaság elemeit. Vagyis az alaphalmaz elemei két osztályba sorolhatók, s az lesz a kérdés, hogy egy véletlenszerűen választott mintában milyen gyakorisággal várható a kétféle elem felbukkanása. Konkrétan a mi feladatunkban a felfedett, illetve a ki nem derített bűntények szerint osztályozzuk a bejelentett bűneseteket. Tudjuk, hogy a 341 061 esetből több mint a fele, 187 655 kiderítetlen maradt. Ez 0,55, vagyis az összes esetnek 55%-a.
Vajon az 1000 ,,véletlenszerűen'' választott eset között hány felderítetlent találunk? Nyilván, ha biztosat akarunk mondani, akkor ez a szám 0 és 1000 között lesz. Vajon, ha egy kis rizikót vállalunk, akkor mennyire csökkenthető ez az intervallum?
Mennyire igaz az, amit sokszor gondolunk, hogy ,,körülbelül'' 55% lesz a mintában is a kiderítetlen esetek száma? Mit jelent itt a ,,körülbelül'' szó, lehet-e valamilyen kvantitatív értelmet adni neki? Mennyire valószínű, hogy például legalább 400 felderítetlen eset lesz?
Látható, hogy a kérdés nagyon hasonló az első problémához. Legalábbis ami a gondolkodásmódot illeti. A számolás sem lesz sokkal nehezebb, de itt is kell majd közelítést használni.
Kíséreljük meg modellezni a problémát. Egyszerű kombinatorikai kérdésről van szó: 341 061 esetből kell kiválasztani 1000 esetet, ami a teljes véletlenszerűség feltételezése mellett (3410611000)-féleképpen tehető meg. Annak az esélye pedig, hogy éppen k felderítetlen eset lesz ezek között, a klasszikus Laplace-féle formulával számolva (kedvező esetek száma osztva az összes esetek számával): (187655k)⋅(153406100-k)(3410611000). Feladatunkra a válasz:
∑k=4001000(187655k)⋅(153406100-k)(3410611000).
Ezt kellene különböző k értékek mellett (0<k<1000) kiszámolni. Nyilván elég fáradságos munka lenne. Ezért érdemes megpróbálni valamilyen közelítést keresni. Azt az eloszlást, amely 0-tól n-ig terjedő természetes számokon értelmezett a következőképpen:
P(X=k)=(Kk)⋅(N-Kn-K)(Nn),k=0,1,...,n
szokás hipergeometrikus eloszlásnak nevezni, lásd pl. [5]-ben.
Ez a következőképpen interpretálható: van N elem (az alapsokaság elemszáma), amelyből K valamilyen megadott tulajdonságú, míg természetesen N-K azon elemek száma, amelyeknek nincs meg az adott tulajdonsága. Eztuán kiválasztunk véletlenszerűen n elemet (ez a minta), s azt kérdezzük, mekkora annak az esélye, hogy éppen k darab lesz (0≥k≥n) a K közül a mintában, feltéve, hogy n<K. Ha X jelöli a tulajdonsággal rendelkezők számát a mintában, akkor éppen az (1) alatti eloszlást kapjuk. A levezetésben valójában egy urnamodellt használunk, csak most eltérően az első problémától, visszatevés nélkül húzunk.
Ha figyelembe vesszük, hogy az urna elemszáma jóval nagyobb, mint a húzások száma, akkor lényegében nem játszik jelentős szerepet a ,,vissza nem tétel''. Ezt felismerve várhatóan jó közelítés lesz a binomiális eloszlás, ahol tehát visszatesszük a húzás után a kihúzott elemet.
Ennek pontos matematikai elemzésére még visszatérünk.
Azaz:
P(X=k)=(Kk)⋅(N-Kn-K)(Nn)≈(nk)⋅(KN)k⋅(N-KN)n-k.
Esetünkben ez konkrétan:
(187655k)⋅(153406100-k)(3410611000)≈(1000k)⋅(187655341061)k⋅(153406341061)1000-k=(1000k)⋅0,55k⋅0,451000-k.
Ezzel már kissé könnyebb számolni. Természetesen számítógéppel kiszámolható az eredmény, de ha az előző részben leírt standard normális eloszlással közelítünk, akkor egyszerű feladat lesz intervallumot megadni előírt rizikó mellett. Mivel esetünben np(1-p)=247,5>9, tehát teljesül a Laplace-kritérium, azért a közelítés ,,megengedett''.
Átlagosan 550 körül lesz a fel nem fedett bűnesetek száma az ezerből, s hogy mekkora intervallumba kell esnie, az a rizikófaktortól függ. Esetünkben nem az intervallum, hanem a rizikófaktor a kérdés. A standard normális eloszlással becsülve adódik:
∑k=4001000(1000k)⋅0,55⋅0,451000-k≈1-Φ(399,5-550247,5)≈1-Φ(-9,57)=Φ(9,57).
Ez a szám viszont már nincs is benne a szokásos Φ táblázatokban, nagyobb mint 0,9999999, vagyis nagyon valószínű.
A binomiális eloszlás normálissal történő közelítéséről már volt szó. A hipergeometrikus eloszlás kapcsolata a binomiális eloszlással jóval könnyebben áttekinthető, ezért itt bemutatjuk. Akik kevésbé érdeklődnek a matematikai levezetések iránt ‐ bár sokszor éppen abból lehet megérteni a dolog lényegét ‐ azok most tovább lapozhatnak a 2. táblázatig.
Az alábbi közelítést szeretnénk megvizsgálni:
P(X=k)=(Kk)⋅(N-Kn-K)(Nn)≈(nk)⋅(KN)k⋅(N-KN)n-k.
A kérdés természetesen az, hogy milyen feltételek mellett lehet ezt használni, illetve mekkora numerikus hibát követünk el. Fejtsük ki a közelítő egyenlőség bal oldalát:
(Kk)⋅(N-Kn-K)(Nn)=(nk)⋅K⋅(K-1)⋅...⋅(K-k+1)N⋅(N-1)⋅...⋅(N-k+1)⋅⋅(N-K)⋅(N-K-1)⋅...⋅(N-K-n+k+1)(N-k)⋅(N-k-1)⋅...⋅(N-n+1)
Erről az alakról már látszik, hogy mi lesz a közelítés lényege, az első tört esetén mindenütt elhagyjuk a kivonandót, mondván, hogy ha K és N nagy, míg n (és ezzel k is) kicsi, akkor k darab K/N szorzata az első tényező. Hasonlóképpen a második tényező esetén a számlálóban minden tényezőt (N-K)-nak véve, míg a nevezőben mindent N-nek véve adódik a közelítés. Aki tanult határérték számítást, az látja, hogy ha n és k fix számok, míg N és vele K tart a végtelenbe (úgy, hogy az arányuk közben állandó maradjon), akkor tényleg határértékben egyenlő lesz a hipergeometrikus eloszlás bármelyik tagja a binomiális eloszlás megfelelő tagjával.
A valóságban azonban K és N nem végtelen nagy, ezért jó lenne megvizsgálni, mekkora hibát követünk el ezzel a becsléssel. Ez nyilván függ N,K valamint n és k viszonyától. Nyilván az utolsó tényezők, azaz K-k+1 és N-k+1 térnek el legjobban K és N-től. A hibának tehát jó felső becslése a (KN-K-k+1N)k⋅(N-KN-N-K-n+k+1N)n-k szorzat. Ennél biztos kevesebbet hibázunk. Ennek értéke: (k-1N)k⋅(n-k-1N)n-k, amit ismét felülről becsülhetünk. Ezúttal az első tényezőben k helyett a legnagyobb lehetséges értéket, n-et írva, és a -1-et elhagyva, valamint a második tényezőben a legkisebb k-t, 0-t írva és ismét elhagyva a -1-et, adódik, hogy a hiba univerzálisan bármelyik tagot nézve, azaz tetszőleges k esetén biztos kisebb, mint (nN)n. Ez egy nagyon durva felső becslés, de még ez is mutatja, hogy nem követünk el nagy hibát, még viszonylag nagy húzás százalék mellett sem.
Esetünkben n=1000, míg N=341061, a hiba kisebb, mint 0,00291000, ami ≈10-2537, azaz elenyésző, ennél a normális eloszlással történő közelítés jóval nagyobb hibát produkál.
Összefoglalva tehát levezetésünket, megállapítható, hogy ha az elemszám legalább egy nagyságrenddel nagyobb a húzásszámnál, akkor semelyik tag közelítésében nem követünk el 0,1n-nél nagyobb hibát, ami legalább öt húzás esetében az eredményt legfeljebb a hatodik tizedesjegyben változtatja meg. Valójában még ennél is kisebb a hiba, nem beszélve arról, ha a húzásszámnál több nagyságrenddel nagyobb az elemek száma. Természetesen, ha ez nem áll fenn, akkor nagy különbségek is felléphetnek, s a közelítés abszolút rossz, lásd például az alábbi esetet:
Legyen egy urnában 20 golyó, 12 piros 8 fehér. 10-szer húzunk visszatevés nélkül. Vajon mekkora eséllyel lesz k piros a húzott golyók között?
Már tudjuk, hogy ezt hogyan számoljuk: az esély= (12k)⋅(810-k)(2010).
A megfelelő közelítés ebben az esetben az a binomális eloszlás lenne, amelynek paraméterei: n=20,p=0,6, azaz annak az esélye, hogy éppen k piros lesz a 10 húzás során: B20;0.6(k)=(20k)⋅0,6k⋅0,410-k.
2. táblázat. Visszatevés nélküli húzás

  Lehetséges értékek    esélyek  0   (120)⋅(810)(2010)=0  1   (121)⋅(89)(2010)=0  2   (122)⋅(88)(2010)=0,0003572  3   (123)⋅(87)(2010)=0,0095261  4   (124)⋅(86)(2010)=0,0750179  5   (125)⋅(85)(2010)=0,2400572  6   (126)⋅(84)(2010)=0,3500834  7   (127)⋅(83)(2010)=0,2400572  8   (128)⋅(82)(2010)=0,0750179  9   (129)⋅(81)(2010)=0,0095261  10   (1210)⋅(80)(2010)=0,0003572

A hipergeometrikus eloszlás számolásakor figyelembe kell venni, hogy ha 10-k>8, akkor a számláló 0 lesz, hiszen nem lehet 8 elemből 9 elemet kiválasztani.
Abban érdemes megállapodni, hogy (nk)=0, ha k>n.

Összehasonlításképpen a binomiális eloszlás megfelelő értékeivel:


  Lehetséges érték    Húzás visszatevéssel    Húzás visszatevés nélkül  0    0,0001    0  1    0,0016    0  2    0,0106    0,0003572  3    0,0425    0,0095261  4    0,1115    0,0750179  5    0,2007    0,2400572  6    0,2508    0,3500834  7    0,2150    0,2400572  8    0,1209    0,0750179  9    0,0403    0,0095261  10    0,0060    0,0003572

A második problémára adott válaszunk tehát az, hogy nagyon nagy (>0,9999999) eséllyel lesz több, mint 400 a fel nem fedett bűesetek száma, amely várhatóan 550 körüli lesz az 1000 esetből, s hogy mekkora intervallumba esik nagy eséllyel (tehát kicsi a rizikója annak, hogy ezen kívül essen) azt ki lehet számítani, ha előre adott, mit akarunk nagy esélyűnek nevezni. Itt is igaz, hogy jelentősen megrövidül az eredeti (0-1000) intervallum, ha egy igen pici rizikót merünk vállalni.
Egyvalamivel még adósak vagyunk, nem mondtuk meg, hogy hogyan lehet véletlenszerűen választani, ami az egész gondolatmenet alapja volt. Gondoljuk meg, ha ez nem teljesül, akkor akár úgy is választhatok, hogy a fel nem fedett bűnesetek közül veszem mind az 1000 esetet, s így biztos, hogy 100% lesz a fel nem derítettek száma.
Egy, a lottónál szokásos lehetőség, az urnából húzás lenne. Ez azonban aligha valósítható meg 341 061 golyóval, közben az egyenletességet folyamatosan keveréssel biztosítva. Jobb lehetőség kínálkozik a számítógépek felhasználásával, amit TV-s játékokból ismerhetünk. Az eljárás a következő: Sorbarendezzük valahogy az összes esetet, az embereket pl. a személyi számuk szerint, majd elkezdjük a gépen a listát ,,futtatni'', s valamikor tetszés szerinti pillanatban a listát megállítani. Ahol éppen tart a futás, az lesz az első elem. Ezután ezt töröljük, s az egész eljárás kezdődik elölről. (Ha nem töröljük az elemet, akkor a visszatevéses eljárás is szimulálható így számítógép segítségével.)
Természetesen itt a megállítás véletlenszerűségére tevődött át a probléma. Ennek biztosítása sem egyszerű. Kis esetszám esetén persze lehet valami ,,igazi véletlen szerint'' megállítani, de mivel a futás hihetetlenül gyors az emberi reakcióidőhöz képest, kis esetszám esetén elég valamikor lenyomni a ,,megállító'' billentyűt, az teljesen véletlenszerű lesz. Nagy esetszámnál lehet, hogy valamiiyen ritmusra állunk be, s ez már esetleg determinisztikussá teszi az eljárást. Jó lenne persze teljesen automatizálni a dolgot, ez is megtehető (legalábbis valamilyen pszeudo-véletlen szinten), de ebben már a számítógép-programozók illetékesek.

Vancsó Ödön ELTE TTK Matematika Szakmódszertani Csoport

Irodalom
[1] Hajnal ‐ Nemetz ‐ Pintér ‐ Urbán: Matematika IV. (B fakt), Tankönyvkiadó, 1982
[2] Császár Ákos: Végtelen sorok, Egyetemi jegyzet, Tankönyvkiadó, 1977.
[3] H. Ch. Reichel: Wahrscheinlichkeitsrechnung und Statistik, Verlag Hölder ‐ Pichler ‐ Tempsky, Wien, 1989
[4] Rényi Alfréd: Valószínűségszámítás, Tankönyvkiadó, 1968
[5] Nemetz Tibor: Valószínűségszámítás, Tankönyvkiadó.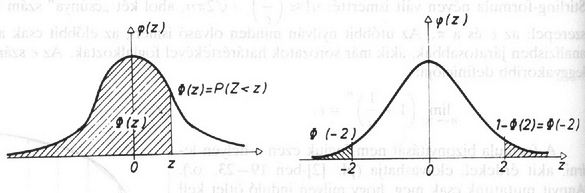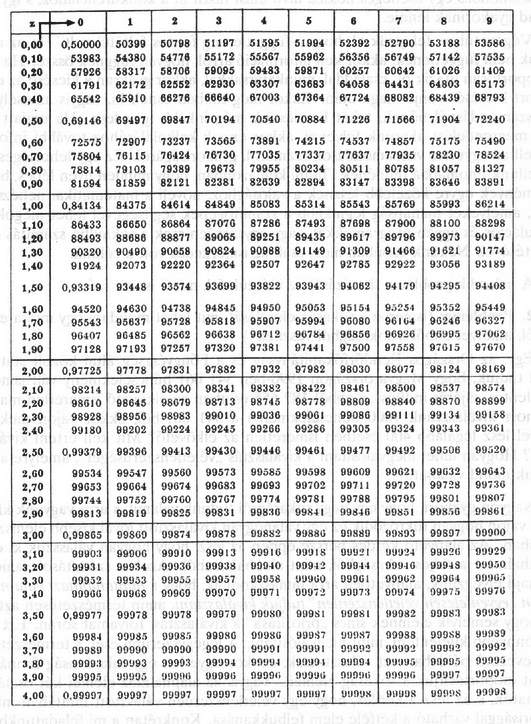