|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.
1. rész
Gauss egyik legnevezetesebb tétele a szabályos sokszög megszerkeszthetőségére mond ki szükséges és elégséges feltételt. Ez a tétel, amelyet a nagy német matematikus 1796 márciusában fedezett fel, a következőképpen szól: a kör kerületét pontosan akkor lehet körzővel és vonalzóval egyenlő részre osztani, ha az prímtényezős felbontásában -hatványon és egymástól különböző Fermat-prímszámok első hatványán kívül más nem fordul elő. A feltételből már gondolhatjuk, hogy itt legfeljebb látszólag van szó geometriai problémáról. Valóban, a geometriai szerkeszthetőséggel kapcsolatos kérdések eddig mindig algebrai eszközök segítségével tisztázódtak. Ez nem meglepő, hiszen a feladat általában az, hogy egy szakaszból annak valahányszorosát akarjuk megszerkeszteni, ennek megoldhatósága pedig láthatóan azon múlik, hogy a kérdéses arányszám kifejezhető-e racionális számokkal, a valós számok közti négy alapművelettel és véges sok négyzetgyökvonással.
Amint ez a címből sejthető, ebben a cikkben a szabályos -szög megszerkeszthetőségére adott feltétel elégségességét fogom bizonyítani, viszonylag elemi számelméleti eszközök felhasználásával. A bizonyítás itt is abból áll, hogy egy arányszám a fenti alakban előállítható. Mielőtt a bizonyításhoz hozzáfognánk, sok mindennel meg kell ismerkednünk. Először a szükséges számelméleti és algebrai alapfogalmakat vezetjük be, majd foglalkozunk a számelmélet egy igen nevezetes tételével, amelynek első bizonyítását szintén Gauss adta, épp egy-két héttel a ,,sokszög szerkeszthetőségi'' tétel bizonyítása után. Ezt az ún. négyzetes (kvadratikus) reciprocitási tételt azután tudjuk kimondani, miután a számelméleti segédeszközöket már ismertettük.
Kezdjük el tehát a szükséges alapfogalmak bevezetését. Fermat-számoknak a alakú egészeket nevezzük, ezek közül a törzsszámokat Fermat-prímeknek mondjuk. Az elnevezést indokolja, hogy Fermat, meggyőződve arról, hogy az említett alakú számok közül a kitevőkhöz tartozóak (vagyis a ) mind prímek, megfogalmazta azt a sejtését, hogy a sorozat minden eleme prím. Ezt elsőként Euler cáfolta meg, igazolva azt, hogy . Ma sem ismeretes, hogy létezik-e végtelen sok Fermat-prím, és az sem, hogy van-e végtelen sok nem prím a Fermat-számok között. Sőt, az említett öt prímszámon kívül jelenleg egyetlen egy Fermat-prímről sem tudunk.
A Fermat-számot -val szokás jelölni, tehát , , stb. E jelölés segítségével egyszerű megfogalmazni azt, amit majd bizonyítani akarunk:
1. Tétel. Ha az prímhatványtényezős előállítása , akkor a kör kerületének egyenlő részre való felosztása körzővel és vonalzóval megoldható.
Legyen egy adott pozitív egész. Az halmazt az elem által reprezentált mod maradékosztálynak nevezzük. Ha , akkor s ezért értelmes a következő definíció: az ún. redukált maradékosztály, ha . Itt hívjuk fel a figyelmet, hogy ezentúl helyett általában a rövidebb jelölést használjuk. A most következő fogalomnak a későbbiekben alapvető szerepe lesz. Mod redukált maradékrendszernek nevezzük egész számoknak olyan halmazát, amelyet úgy kapunk, hogy minden redukált maradékosztályból pontosan egy elemet választunk. A ,,redukált maradékrendszert'' ezentúl RMR-rel rövidítjük. Mod RMR-t alkotnak például az intervallumba eső, -hez relatív prímek is. Itt vezetjük be az Euler-féle függvényt, amely az elemi számelméletben alapvető szerepet játszik. Euler-féle függvénynek nevezzük azt a függvényt, amelyre egyenlő a mod redukált maradékosztályok számával. Természetesen megadható úgy is, mint a mod RMR-ek elemszáma, vagy mint az -be eső -hez relatív prímek száma.
Könnyen látható, hogy pontosan akkor RMR mod , ha egyszerre teljesül az alábbi három követelmény. (A továbbiakban egy számhalmaz ilyen, felsorolásszerűen történő megadásakor a kapcsos zárójelet elhagyjuk.)
Ennek segítségével azonnal ellenőrizhető, hogy ha t1,...,tφ(m) RMR, és (a,m)=1, akkor at1,...,atφ(m) is RMR mod m. Erre az észrevételre a későbbiekben ,,Euler ‐ Fermat-ötlet'' néven fogunk utalni. Rögtön kiderül, mi indokolja ezt az elnevezést. Ennek felhasználásával igazolható ugyanis legegyszerűbben az alábbi, Euler ‐ Fermat-tétel néven ismeretes állítás: Ha (a,m)=1, akkor aφ(m)≡1(m). Valóban, ha t1,...,tφ(m) és at1,...,atφ(m) mindketten RMR-ek, akkor | t1≡atμ(1)(m)t2≡atμ(2)(m)...tφ(m)≡atμ(φ(m))(m) | (1) |
ahol μ az 1,2,...,φ(m) egy permutációja. Az (1) kongruenciákat összeszorozva, majd az m-hez relatív prím ∏i=1ϕ(m)ti szorzattal egyszerűsítve adódik a bizonyítandó aφ(m)≡1(m). Ezt a tételt felhasználva egy fontos tételt fogunk bevezetni. (a,m)=1 esetén legyen k az a legkisebb pozitív egész, amelyre ak≡1(m). Ezt a k kitevőt az a rendjének nevezzük mod m és om(a)-val (vagy, ha nem okoz félreértést o(a)-val) jelöljük (olvasd: ordo a). Könnyen látható, hogy an≡1(m) pontosan akkor teljesül, ha o(a)∣n.
Most pedig ─ a szokásosnál általánosabban ─ definiáljuk az indexeket. Rögzítsünk egy m-hez relatív prím g-t és legyen a olyan, hogy gk≡a(m) egy alkalmas nemnegatív egész k-ra. Ezt a modulo o(g) egyértelműen meghatározott k-t az a szám g alapú indexének nevezzük mod m és ginda-val jelöljük.
Egy újabb alapvető definíció: g primitív gyök mod m, ha o(g)=φ(m). Ezzel kapcsolatban bebizonyítjuk a következőt.
Lemma. Minden prímszámhoz létezik primitív gyök.
Először az alábbiakat látjuk be.
1. Állítás. Az f(x)≡0(p) n-edfokú prímmodulusú kongruenciának legfeljebb n (páronként inkongruens) megoldása van.
2. Állítás. Ha valamely m-re n és k olyan, hogy (om(n),om(k))=1, akkor om(n⋅k)=om(n)⋅om(k).
Az 1. Állítás bizonyítása: Teljes indukciót alkalmazunk az f(x) fokszáma szerint. n=0-ra az állítás nyilvánvalóan igaz. Tegyük fel, hogy minden (n-1)-edfokú kongruenciának maximálisan n-1 megoldása lehet, és legyen grf(x)=n, (ahol grf(x) jelöli f(x) fokszámát). Feltehetjük, hogy f(x)≡0(p)-nek létezik megoldása, legyen az egyik megoldás x1. Ekkor f(x)≡0(p) pontosan akkor igaz, ha f(x)-f(x1)≡0(p), ámde f(x)-f(x1)=∑i=1nai(xi-x1i)=(x-x1)g(x), ahol grg(x)=n-1. Mivel p prím, ezért ha x≢x1(p), akkor szükségképpen g(x)≡0(p). Ez utóbbinak az indukciós feltétel miatt legfeljebb n-1 megoldása van, tehát az f(x)≡0(p) megoldásszáma valóban soha nem nagyobb, mint n.
A 2. Állítás bizonyítása: Ha valamely pozitív egész t kitevőre (nk)t≡1(m), akkor nt⋅o(n)⋅kt⋅o(n)≡1(m), amiért kt⋅o(n)≡1(m). Ennélfogva o(k)∣t⋅o(n), ugyanilyen meggondolás szerint o(n)∣t⋅o(k) is igaz. Innen (o(n),o(k))=1 miatt o(n)⋅o(k)∣t, amiből kapjuk, hogy o(n)⋅o(k)∣o(nk). Viszont o(nk)∣o(n)⋅o(k) is igaz, hiszen (nk)o(n)⋅o(k)≡1(m), amivel beláttuk a 2. Állítást is.
Ezek után igazoljuk a Lemmát. Tekintsük az op(1),...,op(p-1) legkisebb közös többszörösét. Ennek prímfelbontása u=∏i=1rqiαi. Mivel u a rendek legkisebb közös többszöröse, ezért minden i-hez van olyan xi, aminek a rendje aiqiαi alakú. Világos, hogy ekkor o(xiai)=qiαi. A 2. Állításból következik, hogy o(∏i=1rxiai)=u. Ebből a ,,kis''-Fermat-tétel felhasználásával u∣(p-1) adódik. Nyilván xu≡1(p) minden 1≤x≤p-1 esetén. Innen az 1. Állítást figyelembe véve kapjuk, hogy u≥p-1, így tehát u=p-1, vagyis ∏i=1rxiai primitív gyök mod p. |
Gyakranleszszükségakövetkezőre.Könnyűészrevenni,hogyhagprimitívgyök,akkoraz{1,g, g2,...,gφ(m)-1}éppenegymodmRMR.Ellenkezőesetbenugyanislenneolyaniésj,amelyre0≤i<j≤φ(m)-1ésgi≡gj (m),ekkorviszontgj-i≡1 (m)állnafenn,amigprimitívgyökvoltamiattlehetetlen.
Atovábbiakbankizárólagprímmodulusúkongruenciákatszerepeltetünk,ésp-vel‐úgy,minteddig‐csakprímszámotfogunkjelölni.
Legyenp>2és(a,p)=1.Ekkora,,kis''-Fermat-tételbőléspprímvoltábólkövetkezik,hogyap-12≡±1 (p);ap-12≡1 (p)eseténa-rólaztmondjuk,hogykvadratikus maradék,ellenkezőesetbenpedigakvadratikus nemmaradékmodp.Definiáljukaz(ap)ún.Legendre-szimbólumottetszőlegesaegészreakövetkezőképpen: |
(ap) = { 1ha a kvadratikus maradék mod p,-1ha a kvadratikus nemmaradék mod p,0ha p∣a.
|
Nyilvánap-12≡(ap)mod p,sebbőlmindenaésb-re(ap)⋅(bp)= (abp)adódik;ezzelkapcsolatosakövetkeződefiníció.Azf:Z→R,ill.N→Rfüggvénytmultiplikatívnakmondjuk,ha(a,b)=1-bőlkövetkezik,hogyf(a)⋅f(b)=f(ab),ésteljesen multiplikatívnak,haf(a)⋅f(b)=f(ab)tetszőlegesa,begészszámpárrafennáll.Előbbiekszerinttehátaz(ap)Legendre-szimbólumbármelyp>2eseténteljesenmultiplikatív.Etulajdonságfelhasználásávalazonnalbelátható,hogy(egyRMR-enbelül)amodpkvadratikusmaradékokésnemmaradékokszámamegegyezik.Haugyanisgprimitívgyökmodp,akkor(gp)=-1,amiből(gkp)=(-1)k,sígyállításunkvalóbanigaz.Ateljesmultiplikativitásésamostkövetkező‐márkorábbanszóbahozott‐tételteszilehetővékonkrétesetbenaLegendre-szimbólumgyorskiszámolását.
2. Tétel. (Négyzetes reciprocitási tétel.) Legyenek p és q különböző páratlan prímek. Ekkor (pq)⋅(qp)=(-1)p-12⋅q-12.
Más szóval, ha p és q között van 4k+1 alakú, akkor p pont akkor kvadratikus maradék mod q, ha q is az mod p; és ha p is és q is 4k-1 alakú, akkor közülük pontosan az egyik kvadratikus maradéka a másiknak. A prímszámoknak ezt a törvényszerűségét a XVIII. század matematikusai közül már jónéhányan ismerték. Első hiánytalan bizonyítása Gausstól származik, akinek ez a tétel annyira kedvence volt, hogy élete folyamán még további hétféleképpen igazolta. A reciprocitási tételnek ma már kb. 100 bizonyítása ismeretes.
Az 1. Tétel bizonyítása egy olyan tételen ‐ helyesebben szólva annak hátterén ‐ nyugszik, amely a 2. Tétel ‐ egy lehetséges ‐ belátásához is igen jó kiindulásul szolgál. E harmadik tétel felírása előtt azonban bevezetjük a komplex számok és ezen belül a komplex egységgyökök fogalmát. Ezek felhasználásával fogjuk bizonyítani az 1. és a 2. Tételt.
Következik tehát a komplex számok bevezetése, amelyet azért nyújtottam olyan hosszúra, mert bizonyára sokan vannak, akik ezeket idáig még nem ismerték. Most a pontos leírás elolvasása után ők is a megfelelő eszközök birtokában tanulmányozhatják a bizonyításokat.
A komplex számok bevezetése
A valós számok összessége az idők folyamán több szempontból is elégtelennek bizonyult. A legnagyobb hiány az volt, hogy a négyzetgyökvonás nem mindig végezhető el a valós számok (R) körében. A XVI. század olasz matematikusai megtalálták a harmadfokú egyenlet megoldóképletét. Alkalmazása azonban gyakran nehézségekbe ütközött. Amikor ugyanis a vizsgált harmadfokú egyenletnek 3 valós gyöke volt, a képlet használatakor negatív számból kellett négyzetgyököt vonni. Ez inspirációt adott arra, hogy a x(x<0) alakú ,,értelmetlen kifejezéseket'' is tekintsék számoknak, és úgy számoljanak velük, mint ahogy azt addig a valós számokkal tették.
A komplex számok bevezetésének célja lényegében az R-nek egy olyan kibővítése, amelyben (a 0-val való osztást kivéve) elvégezhető a ,,négy alapművelet'', érvényesek a műveleti azonosságok (az összeadás és a szorzás kommutativitása, asszociativitása és a disztributivitás), és van olyan szám, amelynek a négyzete -1.
Nézzük most meg, hogyan lenne célszerű a komplex számokat megkonstruálni. Elsődleges követelmény, hogy legyen olyan i elem, amelyre i2=-1. Könnyen látható, hogy ha ezek között a számok között valóban a megkívánt műveleti azonosságok mellett tudunk összeadni és szorozni, akkor az a+b⋅i(a,b∈R) alakú számok halmaza zárt lesz a két műveletre nézve. A kivonást és az osztást is nyilván el tudjuk végezni, hiszen (a+bi)=(a-c)+(b-d)i+c+di, valamint a+bi=(ac+bdc2+d2+bc-adc2+d2i)⋅(c+di), hacsak c≠0 vagy d≠0. Mindezek alapján úgy tűnik, elég a komplex számok körébe az a+bi alakú ,,számokat'' bevenni, és ezeken értelmezni a szükséges műveleteket. (Meg fogjuk látni, hogy ez tényleg így van.) A definíciók előtt nézzük még meg, mikor lehet egyenlő két komplex szám a támasztott követelmények teljesülése mellett. Tegyük fel, hogy a+bi=c+di. Ha b≠d, akkor i=a-cd-b, ami képtelenség, ugyanis egy valós számnak nem lehet -1 a négyzete. Így csak b=d lehet, amiből egyúttal a=c is következik. Eredményeink alapján megfogalmazzuk a pontos definíciót.
Definíció. Komplex számoknak nevezzük azokat a valós számokból álló (a,b) párokat, amelyekre
(i) (a,b)=(c,d) pontosan akkor, ha a=c és b=d(ii) (a,b)+(c,d)=(a+c,b+d) és (a,b)⋅(c,d)=(ac-bd,ad+bc).
A komplex számok halmazát C-vel jelöljük. Az (ii)-ben megadott két művelet közül az első a komplex számok összeadása, a második pedig a komplex számok szorzása. Felhasználva az R-beli összeadás és szorzás kommutativitását és asszociativitását, valamint a disztributivitást ‐ némi kis számolással ‐ könnyen beláthatók az (ii) alatt definiált műveletekhez tartozó azonosságok is. A következő ‐ szintén lényeges ‐ állítások bizonyítását is az Olvasóra hagyom, ezeket azonban nem nehéz igazolni az R és a C-beli összeadás és szorzás tulajdonságainak figyelembevételével.
a) Létezik egy és csak egy úgynevezett nullelem (jelölje 0), ami olyan (x,y)-t jelent, amelyre tetszőleges (a,b) esetén (a,b)+(x,y)=(a,b). (Ez az (x,y) nyilván a (0,0) lesz.)
b) Minden komplex számnak létezik pontosan egy ellentettje, amin azt a számot értjük, amit az eredeti számhoz hozzáadva 0-t kapunk. Az (a,b) szám ellentettjét -(a,b)-vel jelöljük.
Az a) és b) pontok alapján a komplex számok körében elvégezhető a kivonás, azaz minden (a,b) és (c,d)∈C-hez van olyan egyértelműen meghatározott (x,y)∈C, amelyre (c,d)+(x,y)=(a,b).
c) Létezik C-nek egységeleme, azaz olyan elem, amellyel tetszőleges számot szorozva az eredmény maga az eredeti szám lesz. Az egységelemet a valós esetből megszokott módon itt is 1-gyel jelöljük. Az egységelem 1=1⋅1'=1' miatt egyértelmű (feltettük, hogy 1' is egységelem), és nyilván az (1,0) lesz az.
d) Minden 0-tól különböző (a,b)∈C-nek létezik egyértelműen megadott reciproka (más szóval multiplikatív inverze).
A c) és d) pontokból következik, hogy a komplex számok körében bármely 0-tól különböző számmal lehet osztani is.
Itt érdemes megemlíteni a következő definíciót, amely az algebrában alapvető szerepet játszik. Egy K halmaz a rajta értelmezett + és ⋅ műveletekkel testet alkot, ha a fentebb írt műveleti azonosságok teljesülnek, továbbá + és ⋅ rendelkezik az előbbi a) és b), illetve c) és d) tulajdonságokkal.
A komplex számtestet az R egy alkalmas kibővítésének szántuk. Ezt nem sikerült tökéletesen megvalósítani, hiszen C elemei mind valós számpárok. A konstrukció alapján látszik, hogy C-nek azon elemei, amelyek (a,0) alakúak, ,,éppen úgy viselkednek'', mint a valós számok. Így hát feleltessük meg minden (a,0)∈C számnak az a∈R számot. Ez a leképzés kölcsönösen egyértelmű (más szóval bijektív), ugyanis (i) szerint a=b pontosan akkor igaz, ha (a,0)=(b,0). Megfeleltetésünk művelettartó is, ami azt jelenti, hogy bármely összeg képe egyenlő a tagok képének összegével, és bármely szorzat képe a tényezők képének szorzata. Ezt az (a,0)+(b,0)=(a+b,0) és az (a,0)⋅(b,0)=(a⋅b,0) összefüggések igazolják. Mindezek alapján az (a,0) alakú komplex számokat azonosíthatjuk a valós számokkal, és ennek jegyében (a,0) helyett ezentúl a-t fogunk írni.
A komplex számokat eredetileg a+bi alakúakra terveztük, ahol a,b∈R és i2=-1. Ez lényegében sikerült is. Jelöljük i-vel a (0,1)-et. Ennek négyzete nyilván -1, és ezen i elem segítségével minden (a,b)∈C előállítható a+bi alakban, ugyanis: a+bi=(a,0)+(b,0)⋅(0,1)=(a,b). Ennélfogva a továbbiakban ‐ eredeti elképzelésünkhöz hűen ‐ az (a,b) komplex számot a+bi formában tüntetjük fel.
A következőkben jónéhány, a komplex számok alapvető tulajdonságaival kapcsolatos definíció fog sorra kerülni. Kezdjük az egyik leglényegesebbel. A z=a+bi konjugáltjának nevezzük az a-bi komplex számot, amelynek jelölése z¯. Azonnal látható, hogy az a függvény, amely minden egyes komplex számnak a konjugáltját felelteti meg, bijektív és művelettartó, amellett involutórikus, azaz (z¯)¯=z. Az s(z)=z+z¯ számot a z nyomának, az N(z)=z⋅z¯-t pedig a z normájának nevezzük. Nyilván, ha z=a+bi, akkor s(z)=2a és N(z)=a2+b2, így minden komplex szám nyoma is és normája is valós. Az is látszik, hogy a nyom összegtartó, a norma pedig szorzattartó függvény. Egy komplex szám abszolút értékének nevezzük normájának négyzetgyökét. Ez az elnevezés azért lehetséges, mert bármely valós szám ez új értelemben vett abszolút értéke megegyezik ,,eredeti'' abszolút értékével.
A valós számoknál baj volt, hogy nem lehetett minden elemből négyzetgyököt vonni. Kérdés, hogy nem maradt-e meg ez a gond a komplex számok körében is. Az világos, hogy az összes R-beli elemnek van négyzetgyöke C-ben. Megmutatjuk azonban, hogy tetszőleges z=a+bi komplex számhoz mindig van olyan w=x+iy, amelyre w2=z. A feltételezett (x+yi)2=x2-y2+2xyi=a+bi egyenlőségből adódóan az x2-y2=a; 2xy=b egyenletrendszer megoldásait kell meghatározni. Érdemes észrevenni, hogy a2+b2=N(z)=(N(w))2=(x2+y2)2. Ebből ugyanis x2+y2=a2+b2, innen pedig már rögtön adódik, hogy x2=a+a2+b22 és y2=-a+a2+b22. Mivel a2≤a2+b2, ezért ilyen x és y létezik is. A 2xy=b feltétel miatt x és y csak azonos, illetve csak különböző előjelű lehet, attól függően, hogy b pozitív-e vagy negatív. (Ha b=0, akkor x2=a és y2=0, illetve x2=0 és y2=|a|, attól függően, hogy a pozitív-e vagy sem.) Számolással ellenőrizhető, hogy a w-re kapott két lehetséges érték közül tényleg mindkettőnek z a négyzete.
A valós esethez hasonlóan itt is célszerű egyértelműsíteni egy szám négyzetgyökét. Ezt a következő definícióval érhetjük el. a+bi jelölje azt az x+iy komplex számot, amelynek a négyzete a+bi, emellett vagy x>0, vagy x=0 és y≥0. Az így értelmezett négyzetgyökről már valóban látszik, hogy minden komplex számhoz pontosan egy komplex számot rendel.
A komplex számokat mint valós számokból álló (rendezett) párokat definiáltuk. Ennek alapján fölmerül annak a gondolata, hogy C elemeit valamilyen módon a sík pontjaival, ill. síkvektorokkal azonosítsuk.
Ez legtermészetesebben úgy történhet, hogy felveszünk egy Descartes-féle koordináta-rendszert, és az a+bi számnak megfeleltetjük az (a,b) pontot, illetve azt a vektort, ami a (0,0)-ból az (a,b) pontba mutat. Azt a síkot, amin a komplex számokat ábrázoljuk, Gauss-féle számsíknak nevezzük. Ezt az indokolja, hogy Gauss vezette be a komplex számok geometriai értelmezését. Neki köszönhető az is, hogy a komplex számok elvesztették a XVI. században kialakult misztikus jellegüket, és használatuk meghonosodott a matematikában.
Annak, hogy C elemeit a sík vektoraival azonosítsuk, akkor van értelme, ha a vektorok komplex számként való összeadása ,,ugyanúgy megy'', mint az eredeti vektorösszeadás, vagyis ha C és a síkvektorok közötti, előbb megadott bijekció összegtartó. Ez az összegtartás viszont nagyon könnyen belátható.
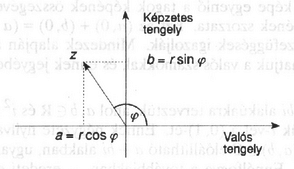
A komplex számok geometriai értelmezésének valódi haszna a szorzás (és ebből adódóan a hatványozás, gyökvonás) elvégzésének megkönnyítéséből ered. A Gauss-féle számsík tetszőleges pontját polárkoordinátákkal is megadhatjuk. (r,φ) annak a z komplex számnak felel meg, amihez tartozó síkvektor hossza r, és az 1-et jelentő egységvektort φ szöggel pozitív (az óramutató járásával ellentétes) irányba elforgatva z-vel egyállású vektort kapunk. Ezt a z≠0 esetén mod 2π egyértelműen meghatározott φ szöget a z szám arkuszának (vagy argumentumának, irányszögének) nevezzük, és arcz-vel jelöljük. A 0 argumentumát nem definiáljuk.
Legyen a z=a+bi számot jelentő vektor hossza továbbra is r, amely nyilván megegyezik z abszolút értékével. Ha φ=arcz, akkor a szögfüggvények definíciójából adódik, hogy a=r⋅cosφ és b=r⋅sinφ, amiből azt kapjuk, hogy z=r(cosφ+isinφ). A z komplex számnak ezt a formáját a szám trigonometrikus alakjának nevezzük. Ez a trigonometrikus alak az, ami a szorzást olyan kényelmessé teszi. Lássuk csak:
z1⋅z2=r1⋅r2⋅(cosφ1+isinφ1)(cosφ2+isinφ2)==r1⋅r2⋅(cos(φ1+φ2)+isin(φ1+φ2))
a közismert addíciós tétel alapján.
Vagyis két komplex szám szorzatának abszolút értéke megegyezik a két szám abszolút értékének szorzatával (ezt már eddig is tudtuk a norma szorzattartásából), és két nem nulla komplex szám szorzatának arkusza mindig a két arkusz összege. Ez a tétel Abraham de Moivre (1667‐1754) Londonban élt francia matematikustól származik, aki a valószínűségszámítás megalapozásában alkotott jelentőset. A Moivre-tétellel kitűnően hatványozhatunk is. Teljes indukcióval rögtön látható, hogy minden természetes n-re zn=rn(cosnφ+isinnφ). Az is nyilvánvaló, hogy 1z=1r(cos(-φ)+isin(-φ)), hiszen ezt kell z-vel szorozni ahhoz, hogy 1-et kapjunk. Így az előző, hatványozásra vonatkozó összefüggést a negatív egész n-ekre is megkaptuk.
Hátra van még a gyökvonás. Legyen n pozitív egész, z≠0, z=r(cosφ+isinφ). Azt állítjuk, hogy az xn=z egyenletet pont azok az x∈C számok elégítik ki, amelyek trigonometrikus alakja x=rn(cos(φ+2kπn)+isin(φ+2kπn)) valamilyen k egész számmal. Hogy ezek az x-ek tényleg megfelelnek, az magától értetődő az előbb zn-re adott képlet alapján. Az állítás másik felét pedig bizonyítja a komplex számtestben is ‐ mint minden testben ‐ érvényes fokszámtétel, ugyanis az x lehetséges értékeit feltételező iménti formula éppen n különböző számot ad.
A gyökvonással kapcsolatban elérkeztünk a bevezető legvégső részéhez, a komplex egységgyökhöz. Legyen n∈N+. Az xn=1 egyenlet megoldásait n-edik komplex egységgyököknek nevezzük. A korábbiakból kitűnik, hogy az n-edik egységgyökök az εk=cos2kπn+isin2kπn sorozatnak az elemei, amelyek a 0 középpontú egységkörön helyezkednek el annak a szabályos n-szögnek a csúcsaiban, amelynek egyik csúcsa az 1-et jelentő pont. A kongruenciánál tárgyaltakkal analóg módon, az egységgyökök körében is definiálható a rend és a primitív (n-edik) egységgyök fogalma. Primitív n-edik egységgyököknek nevezzük azokat az εk n-edik egységgyököket, amelyekre o(εk)=n. Ezekkel kapcsolatban három olyan ekvivalens állítást fogalmazunk meg, amelyek megkönnyítik az n-edik egységgyökök kezelését.
1. εk primitív n-edik egységgyök,
2. εk első n hatványa kiadja az összes n-edik egységgyököt,
3. (k,n)=1.
Könnyen látható, hogy ezek valóban ekvivalensek egymással. |
Fermat-prím a gyűjtőneve a 22k+1 alakú prímeknek.E tétel megfogalmazása a későbbiekben bevezetésre kerülő Euler-féle φ függvény segítségével lényegesen egyszerűbbé válik, ugyanis a fenti feltétel azzal ekvivalens, hogy φ(n) 2-hatvány. Ez a φ(n) explicit alakjának (lásd 5alatt) felhasználásával könnyen belátható. Mi azonban a bizonyítás során nem ebből, hanem a fenti megfogalmazásból fogunk kiindulni.Pierre Fermat (1601. aug. 20.‐1665. jan. 12.). Francia matematikus és fizikus. Elsősorban számelmélettel, geometriával és analízissel foglalkozott.Bizonyára sokan tudják, hogy a≡bmod m és c≡dmod m esetén a+c≡b+dmod m és ac≡bdmod m. (Ez azonnal látható, ha a kongruenciákat átírjuk a megfelelő oszthatósági formulákba.) A kongruenciáknak ezt a tulajdonságát lépten-nyomon fel fogjuk használni.
Leonhard Euler (1707. ápr. 15.‐1783. szept. 18.), a világon az egyik legtermékenyebb matematikus ötletességére jellemző a következő gondolatmenet. Vegyük észre, hogy 641=24+54=5⋅27+1. Ebből 5⋅27=-1mod 641, így tehát 54⋅228≡1mod 641. Ugyanakkor 54≡-24mod 641, ahonnan 232≡-1mod 641 következik, amit látni akartunk. (Persze azért Euler sem azt csinálta, hogy ránézett a 232+1-re és rávágta, hogy osztható 641-gyel. Rendre megnézte a 64k+1 alakú prímeket, hogy melyik osztja 232+1-et, és amikor a 641 sorra került, akkor jöhetett ez az ötlete. Egy későbbi feladat: Miért csak a 64k+1 alakú prímeket kellett néznie?)NemtúlnehézigazolniazEuler-függvénymultiplikativitásátsem.1-tőlab-ig((a,b)=1)felírvaaszámokataoszlopbanésbsorbanúgy,hogyaz1.sorban1-tőla-ig,a2.sorbana+1-től2a-igstb.legyenek,akkorfelhasználvaazt,hogyegyszámpontosanakkorrelatívprímab-hez,haa-hozésb-hezisrelatívprím,márkönnyenbelátható,hogyφ(a)⋅φ(b)=φ(ab).Mivelα≥1eseténφ(pα)=pα-1(p-1),azérthaaznprímtényezőselőállítása∏i=1rqiαi,akkorφ(n)=∏i=1rqiαi-1(pi-1).A fokszámtételt tulajdonképpen már a számelméleti bevezető részben az 1. Állítás címszó alatt bebizonyítottuk, az ott alkalmazott gondolatmenet ugyanis tetszőleges test esetére szóról szóra átvihető. Vegyük észre, hogy az 1. Állítás igazolásakor is lényegében egy testben számoltunk. Tudjuk, bárhogy választunk ki két maradékosztályból egy-egy elemet, azok összege mindig egyazon maradékosztályba esik, és ugyanez igaz a két elem szorzatára is. Ennek alapján a Z-beli műveletek indukálnak egy összeadást és egy szorzást a mod m maradékosztályok között (pl. az [a] és [b] maradékosztályok szorzata nyilván az [ab] maradékosztály lesz). A mod m maradékosztályok a most megadott műveletekkel az ún. mod m maradékosztálygyűrűt alkotják, amelyet Zm-mel, illetve mod m-mel jelölünk. (A maradékosztálygyűrű helyett az algebrában a faktorgyűrű elnevezést is használják.) A gyűrűk a testektől annyiban különböznek, hogy az előbbieknél nem teszünk fel mást a szorzásról, csak az asszociativitást, valamint az így már megkülönböztetendő bal- és jobboldali disztributivitást. Könnyen belátható, hogy Zm pontosan akkor test, ha m prím.
Itt szeretném felhívni a figyelmet egy később előforduló pontatlanságra. Azon például, hogy ,,írjuk Zq elemeit egy g primitív gyök hatványaiként'' azt kell érteni, hogy írjuk az 1,2,...,q-1 RMR elemeit olyan sorrendben, hogy a k-adik elem gk-1-nel legyen kongruens mod q. |
|
 PDF | MathML
PDF | MathML