| Cím: | 1993. A 24. Nemzetközi Fizikai Diákolimpiai feladatainak megoldása | ||
| Szerző(k): | Gnädig Péter | ||
| Füzet: | 1993/november, 404 - 421. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Nemzetközi Fizika Diákolimpia | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Elméleti verseny 1 1. feladat: Légköri elektromosság Elektrosztatikus szempontból a Föld felszínét jó vezetőnek tekinthetjük. A Föld egy bizonyos töltéssel rendelkezik, illetve egy átlagos felületi töltéssűrűsége van. 1. Jó idő esetén a lefelé mutató elektromos térerősség a Föld felszínén hozzávetőlegesen V/m értékű. Határozd meg a Föld felszíni töltéssűrűségének nagyságát, illetve a Föld teljes töltését! 2. A lefelé mutató elektromos tér nagysága a magassággal csökken, és m magasságban körülbelül V/m értékű. Számítsd ki a légkör átlagos eredő töltését köbméterenként a Föld felszíne és a m-es magasság között! 3. Az előző részfeladatban általad kiszámított eredő töltéssűrűség valójában közel azonos számú, egyszeresen töltött pozitív és negatív iontól származik, amelyeknek egységnyi térfogatra eső száma és . A Föld felszínéhez közel, jó idő esetén: . Ezek az ionok a függőleges elektromos tér hatására mozgásban vannak. Sebességük arányos a térerősséggel: 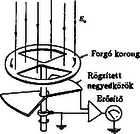 1. ábra 4. A légköri elektromos tér, s így mérésére az egyik lehetőséget az 1.ábrán látható berendezés jelenti. Két negyedkört, amelyek a földtől szigeteltek, de egymással össze vannak kötve, közvetlenül egy egyenletesen forgó, földelt korong alatt rögzítünk. A forgó korongban két negyedkör alakú lyukat vágtunk. (Az ábrán a lemezek távolságát a jobb áttekinthetőség kedvéért felnagyítottuk.) Minden körülfordulás alkalmával a szigetelt negyedköröket kétszer éri teljesen az elektromos tér, illetve (negyed periódussal később) kétszer teljesen árnyékolva lesznek a tértől. 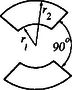 2. ábra Legyen a körülfordulás periódusideje és legyenek a szigetelt negyedkörök belső és külső sugarai és értékűek, amint ezt a 2. ábra mutatja. Legyen az a pillanat, amikor a szigetelt negyedkörök teljesen árnyékoltak. Írj fel olyan kifejezéseket, amelyek és között az idő függvényében megadják a szigetelt lemez felső felületén felhalmozódó töltést. Ábrázold grafikusan is a töltés időbeli változását! (A légköri ionok áramát most hanyagold el!) 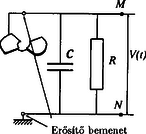 3. ábra 5. Az előző alkérdésben leírt berendezés egy erősítőhöz kapcsolódik, amelynek bemenő áramköre egy párhuzamosan kapcsolt kapacitású kondenzátornak és egy ellenállásnak feleltethető meg (3.ábra). (Feltételezhetjük, hogy a negyedkörökből álló berendezés saját kapacitása elhanyagolható -hez képest.) Vázold grafikusan az és pontok közötti feszültséget az idő függvényében a korong egy teljes körülfordulása alatt, közvetlenül azután, hogy a korong periódusidejű forgásba jött, ha: a) ; b) . (Tételezd fel, hogy és rögzített értékek, csak változik az a) és b) határeseteknek megfelelően!) Adj meg közelítő formulát a arányszámra, ahol és a feszültség legnagyobb értékei az a), illetve b) határesetekben! 6. Tegyük fel, hogy V/m, cm, cm, F, M és a korong másodpercenként fordulatot tesz. Közelítőleg határozd meg, hogy mekkora a feszültség legnagyobb értéke egy fordulat alatt ebben az esetben! Megoldás. 1. Az elektrosztatikai Gauss-törvény értelmében az sugarú Föld felszínére vonatkoztatott teljes elektromos fluxus és a Föld össztöltése között a 2. Képzeljünk el egy alapterületű, m magas függőleges hengert és alkalmazzuk erre Gauss törvényét (4. ábra): 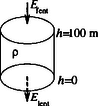 4. ábra 3. Ha egy vezető térfogategységenként darab, egyenként töltésű, töltött részecskét tartalmaz, s ezek sebességgel mozognak, akkor a felületegységre jutó áram, az úgynevezett áramsűrűség 4. Ha -nak választjuk azt a pillanatot, amikor a forgó korong teljesen leárnyékolja a negyedköröket, a külső elektromos mező pillanatnyi fluxusából számolva a kérdezett töltésre adódik, s hasonló kifejezések érvényesek a további félperiódusokban is (5.ábra). 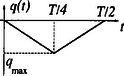 5. ábra A lemezekre kerülő legnagyobb (negatív) töltés: 5. Erre a kérdésre az áramköri egyenletek részletes megoldása nélkül is választ lehet adni. Mindössze azt kell észrevennünk, hogy a negyedkörök töltésének csökkenési sebessége (vagyis a negyedkörökről elfolyó áram) két tag összege: az egyik a kondenzátor töltésének változási sebességével, a másik pedig az ellenálláson átfolyó árammal egyenlő. Attól függően, hogy ezen két mennyiség közül melyik hanyagolható el a másik mellett, két jellegzetes határesetet különböztethetünk meg. a) Ha azaz , az ellenálláson nagyon kevés töltés áramlik át egy periódus alatt. Ebben a határesetben az történik, hogy mialatt a negyedkörök a külső elektromos mező fluxusváltozásának megfelelően egyre több negatív töltéssel kell rendelkezzenek, nyilván csaknem ugyanannyi pozitív töltés kerül a kondenzátorra (hiszen az ellenálláson átfolyó kevés töltést leszámítva az össztöltés állandó marad). A feszültség tehát -tól -ig csaknem lineárisan növekszik, majd ugyanennyi ideig lineárisan csökken (6. ábra). A legnagyobb feszültség ebben az esetben 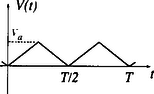 6. ábra b) A másik határesetben . Ilyenkor a töltések könnyen átjutnak az ellenálláson, növekedtekor időben közel állandó pozitív, csökkenésekor pedig állandó nagyságú negatív áram folyik. Az áramerősség nagysága mindkét esetben . Az ellenálláson mérhető feszültség egy-egy negyed-periódusban közelítőleg állandó, előjele pedig váltakozik (7. ábra). A maximális feszültség: 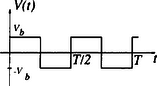 7. ábra A két határeset megfelelő kifejezéseit összevetve: 6. A megadott számértékeknél s, s, vagyis a határeset valósul meg. Az 5. pont a) esetének megfelelő összefüggéseket alkalmazva végül a mV eredmény adódik. 2. feladat: Lézerfény erőhatása átlátszó prizmára 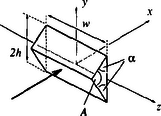 1. ábra A fénytörés következtében egy erős lézersugár számottevő erőt fejthet ki kicsiny átlátszó testekre. Ennek a jelenségnek a bemutatására tekintsünk egy kicsiny, háromszög alakú üvegprizmát, amelynek csúcsponti szöge , alaplapjának hossza , szélessége pedig . A prizma törésmutatója , anyagának sűrűsége . Tegyük fel, hogy a prizmát egy olyan lézersugárba helyezzük, amely vízszintesen az irányban halad. (Az egész feladat során feltehetjük, hogy a prizma nem forog, azaz csúcspontja mindvégig a lézersugárral ellentétes irányba mutat, illetve a háromszög alakú oldallapja mindvégig párhuzamos az síkkal, és alaplapja mindvégig párhuzamos az síkkal, amint ezt az 1. ábra mutatja. A környező levegő törésmutatóját vegyük értékűnek! Tegyük fel továbbá, hogy a prizma oldallapjai visszaverődés elleni bevonattal rendelkeznek, így egyáltalán nem történik visszaverődés.) A lézersugár intenzitása olyan, hogy a -tengely mentén (széltében) egyenletes, azonban az távolsággal lineárisan csökken az tengelytől úgy, hogy a maximális értékét -nál veszi fel, illetve esetén csökken nullára (2. ábra). [Az intenzitás az egységnyi felületre eső teljesítményt jelenti, mértékegysége: .] 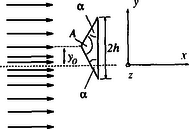 2. ábra 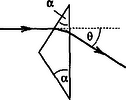 3. ábra 1. A lézersugár a prizma felső lapjára esik (3. ábra). Az tengelyhez képest milyen szögben hagyja el az alaplapot ez a sugár? Elegendő, ha megadsz egy olyan egyenletet, amelyben és szerepel, és amelyből ki lehet fejezni a szöget. 2. Fejezd ki és segítségével a lézersugár által a prizmára ható eredő erő és komponensét, ha a prizma csúcsát távolsággal eltoljuk az tengelytől, ahol (2. ábra). Ábrázold grafikusan az erő vízszintes és függőleges komponensének értékét az függőleges eltolódás függvényében! 3. Tegyük fel, hogy a lézersugár mm széles a irányban, és m keskeny az irányban. A prizma adatai: m, mm, és . Hány watt teljesítményű lézer szükséges ahhoz, hogy ezt a prizmát egyensúlyban tartsa az irányú gravitációs erővel szemben, ha a prizma csúcsa távolságra van a lézersugár tengelye alatt? 4. Tegyük fel, hogy ezt a kísérletet gravitációmentes helyen végezzük el ugyanezzel a prizmával, és a lézernyaláb kiterjedése is ugyanakkora, mint az előző alkérdésben, az intenzitásának értéke azonban . Mekkora periódusidejű rezgéssel mozogna a prizma, ha távolságra tennénk a lézersugár közepétől, és ott magára hagynánk a prizmát a gravitációmentes térben? Megoldás. 1. Ez a részfeladat a fénysugarak törési törvényének (Snellius‐Descartes-törvény) és egyszerű geometriai összefüggéseknek a felírásával oldható meg. 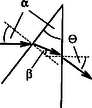 4. ábra Az 4. ábra jelöléseivel: ahonnan 2. A prizmára ható erő a lézersugár lendületének (impulzusának) időegységre eső megváltozásával egyenlő nagyságú, azzal ellentétes irányú vektor. Tekintsük először a prizma felső részére eső fénysugarat és határozzuk meg az impulzusának megváltozását! Ha másodpercenként darab energiájú (vagyis nagyságú impulzussal rendelkező) foton esik a prizmára a negatív -tengely irányából, s szögben eltérülve hagyják el a prizmát, akkor ezen fotonok impulzusának megváltozása: A prizma megfelelő lapjaira eső teljesítményt úgy számíthatjuk ki, hogy az egyes lapok síkbeli vetületének területét megszorozzuk az adott lapra jutó átlagos intenzitással. Ez utóbbit az -tengely mentén szakaszonként lineárisan változó intenzitáseloszlásból és az távolságtól függő geometriai tényezőkből határozhatjuk meg. A nem túl nehéz, de hosszadalmas számolás végeredménye a következő: Két lényegesen különböző esetet kell megvizsgálnunk. a) Ha (a prizma teljes egészében a lézersugár felső felében található), a megfelelő erő-komponensek: b) Ha (a prizma alsó felének egy része belelóg a lézersugár alsó felébe), az erők: 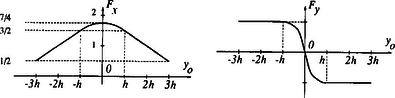 5. ábra Mivel az intenzitáseloszlás szimmetrikus a lézersugár középvonalára, az eset a fentebb leírt eset tükörképe lesz. Az és függvények menetét a 5. ábra mutatja. 3. A megadott számadatokból az üvegprizma súlyára N adódik. A prizma akkor lehet (legalábbis függőleges irányban) egyensúlyban, ha . Az előző pont eredményét és a numerikus adatokat felhasználva a szükséges (maximális) lézer-intenzitásra adódik. A lézer teljes sugárzási teljesítményét az átlagos intenzitásnak és a lézernyaláb keresztmetszetének szorzataként kaphatjuk meg; numerikusan W. 4. elmozdulásnál , a függőleges erőkomponens tehát jól közelíthető az 3. feladat: Elektronnyaláb gyorsítófeszültséggel nagy energiájú elektronok párhuzamos, homogén nyalábját állítjuk elő. Az elektronok útjába egy vékony, hosszú, pozitívan feltöltött rézdrótot helyezünk. 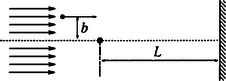 1. ábra. Az elektromosan feltöltött drót merőleges a papír síkjára. Az ábra nem méretarányos. A rézdrót az elektronnyaláb eredeti irányára merőlegesen helyezkedik el (1. ábra). Az ábrán -vel jelöltük azt a távolságot, amennyire egy-egy elektron a rézdrót mellett elhaladna, ha a drótnak nem lenne töltése. Az elektronok ezek után egy ernyőnek csapódnak, amely a drót mögött távolságra helyezkedik el . A nyaláb eredeti kiterjedése a drót tengelyétől mértékű. A drót hossza, valamint a nyaláb szélessége a papír síkjára merőlegesen végtelen nagynak tekinthető. Megjegyzés. A 2‐4 alkérdések esetén alkalmazz olyan elfogadható közelítéseket, melyek segítségével képlet formájában és numerikusan is eljuthatsz a megoldásig. 1. Számítsd ki a drót által létrehozott E elektromos térerősséget! Ábrázold vázlatosan E nagyságát a drót tengelyétől mért távolság függvényében! 2. Számítsd ki, hogy mekkora szöggel térül el egy elektron a klasszikus fizika törvényei szerint! Add meg ezt az eltérülési szöget a 3. Számold ki és vázold is fel, hogy a klasszikus fizika milyen becsapódási képet (azaz elektronintenzitás-eloszlást) jósol az ernyőre érkező elektronokra! 4. A kvantumfizika a klasszikus elmélettől lényegesen különböző elektronintenzitás-eloszlást jósol. Vázold fel a hullámmechanika által jósolt eloszlásképet és számszerűen is jellemezd ezt az elektroneloszlást! Megoldás. 1. A hengerszimmetria miatt az elektromos térerősség a dróthoz képest sugárirányú kell legyen és a nagysága csak a dróttól mért 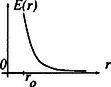 2. ábra 2. A feladat szövege szerint az elektronok A merőleges impulzus értékére a következő nagyságrendi becslés adható: A haladás irányára merőleges erő nagysága (a drót közelében, vagyis ott, ahol a hatása számottevő) Pontosabb és elméletileg jobban megalapozott becslést kapunk, ha az elektronok (egyeneshez közeli) pályájának minden részén figyelembe vesszük a merőleges erőhatást, s ezek járulékait összegezve számítjuk ki a merőleges impulzusváltozást. 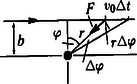 3. ábra A 3. ábra jelöléseit használva ahonnan 3. Az elektronok pályagörbéje két olyan egyenessel közelíthető, melyek a drót közelében megtörnek, hajlásszögük a fentebb kiszámított  4. ábra az ábra nem méretarányos Az átfedő tartomány szélessége 4. A kvantumelmélet (de Broglie hipotézise) szerint a  5. ábra A drót jobb oldalán két, egymással kicsiny Kísérleti verseny 1 1. feladat: A nitrogén forráshőjének mérése A mérés tárgya a nitrogén A rendelkezésre álló folyékony nitrogén egy ,,tároló'' tartályban van. Ebből tölthetsz megfelelő mennyiséget a ,,minta'' tartályba, amit a mérlegre kell helyezned. A mérlegen leolvasható tömeg a nitrogén forrása következtében egyre csökken. Ennek több oka van: Egy univerzális mérőműszer (multiméter), amely feszültség FIGYELEM: (1) A folyékony nitrogén nagyon hideg, tehát semmilyen körülmények között ne érj hozzá, és azokhoz a testekhez sem, amelyeket nitrogénnel lehűtöttél! Vigyázz, hogy a ruhádra se kerüljön folyékony nitrogén! (2) Semmit ne dobj a folyékony nitrogénbe, és mindvégig viseld a védőszemüveget! (3) Az alumínium-darabkát lassan merítsd a nitrogénbe, mivel egyébként túlságosan heves forrásba jönne a folyékony nitrogén. A bemerítéshez használd a mellékelt zsineget! (4) Az ellenállás nagyon felforrósodhat, ha nem merülne a folyékony nitrogénbe. Csak akkor engedj át áramot az ellenálláson, ha az a tartályban van, és teljesen ellepi a folyékony nitrogén! 1. módszer 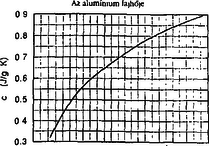 1. ábra Az alumínium Végezz méréseket, melyek alapján meghatározhatod, mennyi nitrogén forr el az alumíniumdarab lehűlése során! Mérési eredményeid, valamint a fajhőgrafikon felhasználásával határozd meg a nitrogén forráshőjét! Feltételezheted, hogy a szobahőmérséklet 2. módszer Végezz méréseket, amelyek alapján meghatározhatod a folyékony nitrogén forrásának sebességét, amikor áram folyik át a nitrogénbe helyezett ellenálláson. (Egyenáramú tápegység áll rendelkezésedre.) Eredményeid alapján határozd meg a nitrogén forráshőjét! Feltétlenül adj számításon alapuló hibabecslést az általad mért mennyiségre! Megoldás. 1. módszer. A rendszer (tárolóedény + folyékony nitrogén + később belehelyezett alumíniumdarabka) tömegét és az időt folyamatosan mérve pl. a 2. ábrán látható adatokat kapjuk. 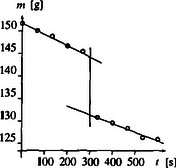 2. ábra Az alumíniumdarabka behelyezését megelőző, majd az azt követő időszak adataira jó közelítéssel egyeneseket illeszthetünk. (Vigyázat: a két egyenes meredeksége egy kicsit különbözik, hiszen a kisebb tömegű nitrogén kisebb felületen érintkezik a tárolóedény falával, s emiatt a hőátadás is lassabb, mint kezdetben. Azok a versenyzők, akik erre a ,,finomságra'' nem figyeltek fel, pontot veszítettek.) Az egyeneseket az alumíniumdarabka behelyezésének pillanatáig extrapolálva a függvény ugrásából megkapjuk a szilárd test által leadott Az egyik mérési sorozatban numerikusan a következő értékeket kapták: 2. módszer. Mérhetjük a rendszer tömegének időbeli változását elektromos fűtés nélkül, rövid ideig bekapcsolt fűtéssel, majd ismét fűtés nélkül (3. ábra). 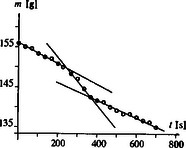 3. ábra Az egyes szakaszokra egyeneseket illesztve leolvashatjuk a folyékony nitrogén tömegének átlagos változási ütemét. A fűtés nélküli szakaszok adatait extrapolálva megkapjuk a fűtés ideje alatti hőveszteség által elforralt nitrogén tömegét, illetve az ismert (mérhető) nagyságú elektromos energia által elforralt nitrogén 2. feladat: Mágneses nyomatékok és mágneses terek mérése Ez a kísérlet két részből áll: 1. részfeladat. Meg kell határoznod egy kisméretű, henger alakú állandó mágnes mágneses nyomatékának nagyságát. Ez a mágnes az ,,X'' jelű borítékban található. (Egy hasonló mágnest, amit szintén használnod kell, az ,,A'' jelű borítékban találhatsz meg.) 2. részfeladat. Egy tengely-szimmetrikus mágnes mágneses terét kell megvizsgálnod. Ez a mágnes a ,,B''-jelű borítékban található. Méréseid során felhasználhatod az alábbiakat: 1. Egy mágneses dipól mágneses tere a szimmetriatengely mentén, a mágnes középpontjától  ahol B mértékegysége tesla 2. Egy szabadon felfüggesztett, vízszintes mágnes (a Föld mágneses terében mozgó iránytűhöz hasonló) kicsiny torziós lengéseinek periódusideje: A mérőberendezés 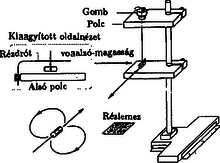 1. ábra 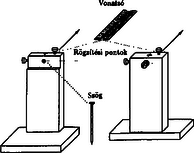 2. ábra A mérőberendezés vázlata az 1.ábrán látható. Egy faállvány felső polcáról egy fonál lóg lefelé. A fonál alsó végéhez mágnest (akár az ,,X'', akár pedig az ,,A'' jelűt) rögzíthetünk. Az alsó polcra egy rézlemezt helyezhetsz, éppen a felfüggesztett mágnes alá, így ha szükséges, csillapíthatod a mágnes mozgását. Két további (segéd-)faállvány is rendelkezésedre áll. Ezek egyikét arra használhatod az 1. részfeladatnál, hogy akár az ,,A'', akár az ,,X'' mágnest tartsa. A másik faállvány a 2. részfeladatnál a ,,B'' jelű mágnesrendszer rögzítésére szolgál. A felfüggesztett mágnes és a segédállvány közötti távolságot vonalzóval mérheted meg; a vonalzót a 2. ábrán nyíllal megjelölt helyre rögzítheted. Figyelem! Ezek a mágnesek nagyon erősek. Tartsd erősen a mágneseket, nehogy kiugorjanak a kezedből! 1. részfeladat. Az ,,X''-jelű borítékban egy mágnespár található, melynek végeit betű-szám kombinációval jelöltük meg. Ennek az összetett rendszernek a Az ,,A''-jelű borítékban egy másik mágnespár van, amelynek északi pólusát fekete, déli pólusát piros folttal jelölték meg. Ez a mágnespár hasonló az ,,X''-belihez, bár a Bármelyik mágnespár darabjait ,,szétcsúsztathatod'', közéjük bronzkorongot helyezhetsz, amely segítségével a fonál végéhez rögzítheted a rendszert. Így ,,iránytűt'' készíthetsz, melynek torziós lengésidejét meg tudod mérni. (Az ,,X'' borítékon feltüntetett A faállvány lyukába helyezve valamelyik mágnespárt, hatást tudsz gyakorolni az ,,iránytű''-mágnespárra: - megváltoztathatod a torziós lengéseinek periódus idejét, - megváltoztathatod az iránytű egyensúlyi helyzetének szögállását. A szögelfordulást legjobban úgy figyelheted meg, hogy néhány milliméterrel az ,,iránytű'' alá helyezed a rézlemezt, s így elektromágneses csillapítást hozol létre. Kérjük, hogy a rézlemezre ne írjál, s jeleket se tegyél rá! Vedd észre, hogy nem elég egyféle mágnes-elrendezéssel dolgoznod! Rajzolj világosan azonosítható ábrákat az általad használt összes kísérleti elrendezésről! Írd le azokat az egyenleteket is, amelyek kapcsolatot teremtenek az egyes elrendezésekben mérhető mennyiségek és a keresett Az összes mágnes mindvégig ugyanabban a vízszintes síkban kell maradjon! Megjegyezzük, hogy a polcos faállvány felső lapján lévő gomb elforgatható, továbbá a fonál hossza változtatható. Mindkét polc helyzete változtatható. 1. Iránytű-elrendezés és használata: Tartsd az adott mágnespár egyik mágnesét a hüvelyk- és a mutatóujjad között. Helyezd a mágnes egyik végére a bronzkorongot! Ezután óvatosan, a fonál megfeszítése nélkül, érintsd oda a másik mágnest is. Így állítsd össze az (,,A'' vagy ,,X'') iránytű-párt. Hasonlóan járj el az iránytű szétszedésekor is, ne feszítsd meg a fonalat! Vigyázat: A mágnesek, vagy mágnespárok hirtelen összecsattanása elszakíthatja a fonalat, vagy összetörheti a mágnest. Ha mégis elszakadna a fonál, kicsi hurokkal kösd meg! (Szükség esetén fordulj a rendezőkhöz!) 2. Csak a forgási (torziós) rezgésekkel foglalkozzál! Az ,,inga-módus'' elkerülése érdekében egy kis rézdrótot erősítettek a tartóállvány alsó polcára. Ezt a drótot forgasd el úgy, hogy a vízszintes része éppen hozzáérjen a fonálhoz, körülbelül 2 mm-rel a fonálon levő csomó felett. Fordítsd tovább óvatosan a drótot ugyanabba az irányba még egy-két mm-rel! Vigyázat: Ha ezt nem teszed, a kétféle rezgési módus ,,összecsatolódik'', periodikusan változtatva a torziós lengés amplitúdóját és befolyásolva a periódusidejét. A torziós lengéseket a 2. ábrán látható szöggel indíthatod el. 3. A mágneses vagy mágnesezhető tárgyakat ne mozgasd el a mérés ideje alatt, s lehetőleg tartsd ezeket minél messzebb a kísérleti berendezéstől! Ilyen tárgyak például: szög, karóra, toll stb. Az asztal egyes részei vasból készültek, ha megváltoztatod a berendezés helyzetét, ezt a tényt is vedd figyelembe! Javaslatok: i) A fonál torziómodulusza elég kicsi. A fonál csavarodásának hatását emiatt elhanyagolhatod, ha a fonál elegendően (körülbelül 15 cm) hosszú. ii) Előfordulhat, hogy valamelyik mágnespár nem vízszintes helyzetben lóg. Ezt a Föld mágneses terének függőleges összetevője okozza. Ennek hatása kicsiny és elhanyagolható. Más szóval: a mágnest vízszintesnek tekintheted! iii) Azt tanácsoljuk, hogy az 1. részfeladat hibaszámítását halaszd későbbre; csak a 2. részfeladathoz szükséges mérések elvégzése után számolj hibákat. iv) Semmiféle feltevést nem szabad tenned a Föld mágneses terének nagyságáról! 2. részfeladat. A ,,B'' borítékban lévő alumíniumcső hengerszimmetrikus elrendezésű mágneseket tartalmaz. Ennek a mágnesrendszernek az  3. ábra Megoldás. 1. részfeladat. Az ,,X'' jelű mágnespárt felfüggesztve és meglengetve (4. ábra), a  4. ábra  5. ábra Ha most az ,,A'' jelű mágnespárból készítünk iránytűt, hagyjuk, hogy beálljon észak-dél irányba, majd az ,,X'' jelű mágnest az északi (vagy a déli) irányból óvatosan közelítjük az iránytűhöz, egy bizonyos (jól mérhető) 2. részfeladat. Az ismeretlen a) Közepesen nagy távolságoknál az ,,X'' mágnespárból készített iránytű lengésidejét, illetve a lengésidő változását mérhetjük az alumíniumcső különböző helyzeteiben. Érdemes az alumíniumcsőbe rejtett mágnesekkel először gyorsítani, majd lelassítani az ,,X'' jelű mágnes torziós lengéseit (6. ábra).  6. ábra Könnyen belátható, hogy a keresett indukció a b) Kicsiny távolságoknál a fenti módszer nem alkalmazható, mert az iránytű lengése nagyon gyorssá válik, illetve a ,,B'' jelű mágnes magához rántja a másik mágnest. Ilyenkor célszerű a ,,lenullázós'' módszert választani, vagyis az ,,A'' jelű mágnesből készített iránytűt a ,,B'' és az ,,X'' jelű mágnesek alkalmas elhelyezésével éppen kifordíthatjuk az észak‐déli irányból (7.ábra).  7. ábra Amikor ez bekövetkezik, akkor fennáll, hogy c) Nagy távolságoknál a legelső módszer javított változata a legcélszerűbb. Most is az ,,X'' jelű mágnes torziós lengéseit, azok megváltozását mérjük, de ez a változás (A három módszer következetes alkalmazását az adott idő (2,5 óra!) alatt nyilván nem lehetett a versenyzőktől elvárni; itt most csak a teljesség igénye, a mérési feladatban rejlő finomságok kiemelése miatt írtuk le ezeket. A versenyzők szinte kivétel nélkül csak az egyik, általában az a) módszerrel határozták meg a mágneses indukciót.) 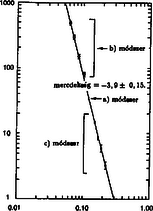 8. ábra A mérési adatokból a Megjegyezzük, hogy az alumíniumcsőben két ‐ közel egyforma ‐ mágnest helyeztek el egymással szembefordítva. Ezek eredő mágneses dipólnyomatéka nulla, az eredő mágneses tér (a mágnesektől viszonylag messze) kvadrupól-jellegű, erőssége a szimmetriatengelye mentén 1A rendelkezésre álló idő: 5 óra.1 A rendelkezésre álló idő: 2 x 2,5 óra |