Kezdőlap


Cím:	Forgási egyenlet tetszőleges tengelyre
Szerző(k):	Szvetnik Endre
Füzet:	1993/május, 227 - 232. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Forgási egyenlet ‐ tetszőleges tengelyre^{$^{*}$}

Bevezetés

A merev testek forgómozgásával kapcsolatos nehezebb problémák, versenyfeladatok többségében síkbeli mozgást vizsgálunk.^{$^{*}$} Általában úgy járunk el, hogy a tömegközéppontra vonatkozó tételeket írjuk fel, illetve figyelembe vesszük a kényszerfeltételeket:

\begin{matrix} {\vec{F}}_{eredő}^{k} = m \cdot {\vec{a}}_{T K}, M_{T K}^{k} = Θ_{T K} \cdot β, + kényszerfeltételi egyenletek . \end{matrix}

(1)

Sokszor a forgási egyenletet másfajta tengelyekre is alkalmazzák, ennek jogossága azonban egyáltalán nem magától értetődő. Ezen megoldások egységes elvi alapját keresve jutottam el a tetszőleges tengelyre érvényes forgási egyenlethez, melynek segítségével a forgástengely éppen olyan szabadon választható, mint a statikában

^{[1]}

. Ebből az egyenletből az is következik, hogy nem általános érvényű az a közismert tétel, miszerint a pillanatnyi forgástengelyekre mindig felírhatjuk az

\begin{matrix} M = Θ \cdot β \end{matrix}

(2)

egyenletet, ahol

M

a külső erők forgatónyomatéka a pillanatnyi forgástengelyre^{$^{*}$},

Θ

pedig ugyanezen tengelyre vett tehetetlenségi nyomaték

^{[2,3,4,5]}

Cáfolat és a helyes tétel

A hibás (2) "tételnek'' az elemzése elvezet bennünket a címbeli egyenlethez. A (2) egyenlet alkalmazhatóságát azzal szokták indokolni, hogy a pillanatnyi forgástengely körüli síkmozgás egy rövid ideig rögzített tengely körüli forgásként kezelhető. A hiba az, hogy ez a helyettesítés általános esetben csak a sebességeket adja vissza helyesen, a gyorsulásokat nem! Gondoljuk csak meg, a "test'' pillanatnyi forgástengelyre eső pontja^{$^{*}$} általában gyorsul, a rögzített tengelyen fekvő pont pedig nyilván nem. (Onnan is látszik a (2) egyenlet "gyanús'' volta, hogy egy olyan feltételre ‐ a forgástengely pillanatnyi sebességének hiányára ‐ hivatkozik, amely teljesülése, vagy nem teljesülése függ a megfigyelő abszolút sebességétől. Ha az egyik megfigyelő az

A

pontot éppen nyugvónak látja, a hozzá képest egyenesvonalú, egyenletes mozgást végző másik megfigyelő szerint ugyanezen pont nincs nyugalomban. Node Galilei óta tudjuk, hogy a mechanika törvényei a különböző inercia-rendszerekben ugyanúgy néznek ki, alakjuk megegyezik. Ez a Galilei-féle relativitás-elv.)

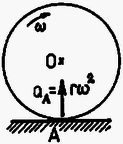1. ábra

Példaként tekintsük egy

r

sugarú karika csúszásmentes gördülését vízszintes síkon! Ha a mozgás szögsebessége

ω

, az

A

pont gyorsulása

a_{A} = r \cdot ω^{2}

nagyságú, az

O

geometriai középpont felé irányuló vektor (1. ábra). Ez közvetlenül adódik, ha a tiszta gördülést két mozgás (

O

-val való haladó mozgás és

O

körüli forgás) szuperpozíciójaként állítjuk elő.^{$^{*}$} A rögzített tengelyű forgásra érvényes alapegyenlet bizonyítása kihasználja

^{[6]}

, hogy a rögzített tengelyre eső pont zérus gyorsulású. Példánkból kitetszik, hogy ez a feltétel a pillanatnyi forgástengelyre nem minden esetben teljesül.

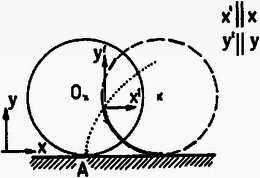2. ábra

Folytassuk az elemzést úgy, hogy képzeletben beülünk egy gyorsuló koordinátarendszerbe! Valamely időpillanatban megjelöljük a test

A

pontját, s ha vele együtt mozgunk, rögzített forgástengelyű mozgást látunk. Ennek a forgásnak a szöggyorsulása ugyanakkora, mint az inercia-rendszerbeli szöggyorsulás, ha a koordináta-tengelyek nem fordulnak el az eredeti rendszer tengelyeihez képest (2. ábra). Így tehát, ha a külső (valódi, más testekkel való kölcsönhatásból származó) erők forgatónyomatékához hozzáadjuk a tehetetlenségi erők forgatónyomatékát

^{[7]}

, a pillanatnyi forgástengelyre vonatkozó helyes forgási egyenletet kell kapjuk.
Gondolatmenetünkben sehol nem használtuk ki, hogy

A

zérus sebességű, így a "test'' tetszőleges

P

pontján átmenő tengelyre fennáll az alábbi forgási egyenlet:

\begin{matrix} M_{P}^{k} + M_{P}^{{(- m {\vec{a}}_{P})}_{T K}} = Θ_{P} \cdot β, \end{matrix}

(3)

ahol

M_{p}^{k}

a külső erők forgatónyomatéka,

M_{P}^{{(- m {\vec{a}}_{P})}_{T K}}

a tömegközéppontban ható

{(- m {\vec{a}}_{P})}_{T K}

tehetetlenségi erőnek a forgatónyomatéka a tetszőlegesen választott tengelyre,

Θ_{P}

pedig ugyanezen tengelyre vonatkozó tehetetlenségi nyomaték. (Természetesen

{\vec{a}}_{P}

P

pont gyorsulásvektora,

m

a test tömege,

β

pedig a szöggyorsulása.)
Mivel a gyorsuló koordináta-rendszerekkel való számolás szabályait nem mindenki ismeri, érdemes egy inercia-rendszerbeli bizonyításra is utalni. Induljunk ki a tömegközépponti tengelyre felírt forgási egyenletből:

\begin{matrix} M_{T K}^{k} = Θ_{T K} \cdot β . \end{matrix}

(4)

Adjunk hozzá mindkét oldalhoz

m d^{2} β

-t, ahol

d

a tetszőlegesen választott tengely és a tömegközépponti tengely távolsága. Így

\begin{matrix} M_{T K}^{k} + m d^{2} β = Θ_{P} \cdot β \end{matrix}

(5)

adódik, ahol felhasználtuk a Steiner-tételt

^{[8]}

is. Ha most a forgatónyomatékot átszámítjuk a tetszőlegesen választott tengelyre, továbbá a tömegközéppont gyorsulását kifejezzük a

P

pont gyorsulásával, éppen a (3) egyenletet kapjuk.

Diszkusszió

Vizsgáljuk meg, milyen esetekben kapunk helyes eredményt, ha (3)-ban csak a külső erők forgatónyomatékával számolunk, a tehetetlenségi erők nyomatékáról pedig megfeledkezünk.
a)

P = T K

, vagyis a forgástengely átmegy a tömegközépponton. A tehetetlenségi erőknek ilyenkor nyilván nincs forgatónyomatéka

P

-re; megkaptuk a tömegközépponti tengelyre érvényes forgási egyenletet.
b)

{\vec{a}}_{P} = 0

; több megoldás ilyen tengelyt használ, ezért adódik helyes eredmény

^{[9,10]}

.
c) A tömegközéppont az

{\vec{a}}_{P}

egyenesére esik

^{[11,12]}

. Homogén henger csúszás-mentes gördülésére ez a feltétel teljesül, ezért alkalmazható a (2) tétel ezekre a problémákra.^{$^{*}$}

Alkalmazás

Az alábbiakban egy olyan problémát fogunk megoldani, amelyre az (1) és (2) módszer különböző eredményt ad, a (3) egyenlet célszerű alkalmazása pedig jelentősen leegyszerűsíti a szükséges számolást.

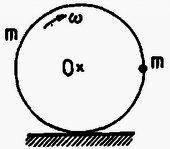3. ábra

A probléma a következő: Egy

m

tömegű,

r

sugarú karikához egy szintén

m

tömegű, pontszerűnek tekinthető testet erősítünk. A rendszer vízszintes síkon csúszásmentesen gördül, s amikor a pontszerű test egy magasságban van az

O

geometriai középponttal, a szögsebesség adott

ω

nagyságú (3. ábra). A kérdés: Mekkora a rendszer szöggyorsulása?
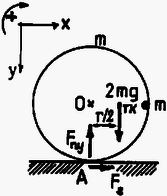
Az (1) módszerrel a következő egyenletrendszert kapjuk (4. és 5. ábra):

\begin{matrix} (6 a) & F_{s} & = 2 m \cdot a_{x}^{T K}, & (6 d) & a_{x}^{T K} & = a_{0} - \frac{r}{2} ω^{2}, \\ (6 b) & 2 m g - F_{n y} & = 2 m \cdot a_{y}^{T K}, & (6 e) & a_{y}^{T K} & = \frac{r}{2} \cdot β, \\ (6 c) & F_{n y} \cdot \frac{r}{2} - F_{s} \cdot r & = \frac{3}{2} m r^{2} \cdot β, & (6 f) & a_{0} & = r \cdot β . \end{matrix}

Az egyenletrendszer megoldása:

\begin{matrix} β = \frac{g + r ω^{2}}{4 r} . \end{matrix}

(7)

4. ábra

5. ábra

A(2) egyenletet a jelen problémára alkalmazva (4. ábra):

\begin{matrix} 2 \cdot m g \cdot \frac{r}{2} = 4 m r^{2} β, \end{matrix}

(8)

ahonnan

\begin{matrix} β = \frac{g}{4 r} . \end{matrix}

(9)

Természetesen a meglehetősen hosszadalmas, de biztosan érvényes (1) módszerrel kapott (7) kifejezés a helyes eredmény, így a (2) ''tételnek'' egy ellenpéldával való cáfolatát kaptuk.

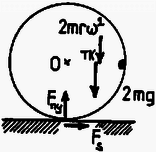6. ábra

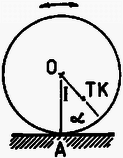7. ábra

A (3) módszer esetén ‐

P

-t az

A

pontba választva ‐ egyetlen egyenlet megadja a helyes szöggyorsulást (6. és 1. ábra):

\begin{matrix} 2 m g \cdot \frac{r}{2} + 2 m r ω^{2} \cdot \frac{r}{2} = 4 m r^{2} \cdot β . \end{matrix}

(10)

Ha a

P

pontnak az

O

pontot választjuk, akkor elegendő lenne csupán a külső erők forgatónyomatékával számolnunk (lásd a diszkusszió c) pontját). Ez azonban nem túl hasznos választás, hiszen a tapadási súrlódási erőt nem ismerjük (s ennek a külső erőnek van forgatónyomatéka az

O

pontra).
A (3) egyenlet hasznosságát egy másik példán is bemutathatjuk^{$^{*}$}: Egy

m

tömegű, inhomogén henger vízszintes síkon való csúszásmentes "rezgését'' vizsgáljuk (7. ábra). Az ábrán látható helyzetben a szögfordulás a középhelyzethez képest

α

, a szögsebesség pedig

ω

. Vajon mekkora a henger szöggyorsulása?

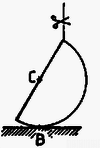8. ábra

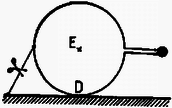9. ábra

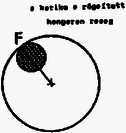10. ábra

A megoldást most is egyetlen egyenletből kaphatjuk, ha a

P = A

választással élünk:

\begin{matrix} Θ_{A} \cdot β = (m g + m r ω^{2}) \cdot ι sin α . \end{matrix}

(11)

(Érdemes kiszámolni a tömegközépponti módszerrel is a szöggyorsulást.)

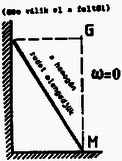11. ábra

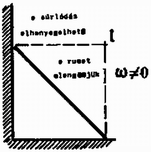12. ábra

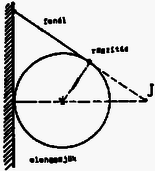13. ábra

A (11) egyenlet jól használható az 1992. évi Eötvös verseny I. feladatánál is, melynek az (1) módszerrel történő megoldása a KöMaL múlt havi számában olvasható

^{[16]}

. Végül ábrák segítségével (8-13.ábra) bemutatunk még néhány tanulságos feladatot^{$^{*}$}, (a problémák teljes szövege az irodalomjegyzék alapján kikereshető). Kérdésem az Olvasóhoz: a megjelölt tengelyek esetén elegendő-e csupán a külső erők forgatónyomatékával számolni? Ha igen, akkor a diszkusszióban felsorolt pontok közül melyik indokolja ezt az egyszerűsítést? [A helyes válaszok: B ‐ igen, a b) pont miatt; C ‐ nem; D ‐ igen, b); E ‐ igen, c); F ‐ igen, c); G ‐ igen, b); H ‐ nem; I ‐ igen, c); J ‐ igen, b).] Az indoklással önállóan próbálkozzon az Olvasó! Remélem, hogy módszerem ‐ amely a tömegközépponti tengelyre vonatkozóhoz hasonlóan univerzális érvényű ‐ áttekinthetőbbé teszi a merev testek síkmozgásának tárgyalását, tisztáz bizonyos elvi kérdéseket, és olykor a gyakorlatban is egyszerűbbé teszi a számításokat.

IRODALOMJEGYZÉK

[1]	Dede Miklós ‐ Isza Sándor: Fizika II. Tankönyvkiadó, Budapest, 1982. 149. o.

[2]	Dede Miklós: Kisérleti fizika (Egyetemi jegyzet). Tankönyvkiadó, Budapest, 1975. I. kötet 199. o.

[3]	Nagy László: Testek gördülése, haladó és forgómzgás együttes fellépése II. KöMaL 37. kötet (1968) 34. o.

[4]	Fizika és számítástechnika ‐ Mechanika. NOVOTRADE RT., 1987. 110. o.

[5]	Cseresznyés Zoltán ‐ Benkő Zsigmond: Fizika 31.o.

[6]	Dede Miklós ‐ Isza Sándor: Fizika II. Tankönyvkiadó, Budapest, 1982. 133. o.

[7]	Dede Miklós ‐ Isza Sándor: Fizika II. Tankönyvkiadó, Budapest, 1982. 146. o.

[8]	Fizika és számítástechnika ‐ Mechanika. NOVOTRADE RT., 1987. 110. o.

[9]	(Az 1982. évi Eötvös verseny 1. feladatának megoldása, (II. módszer) KöMaL, 66. kötet(1983) 81. o.

[10]	(1561. feladat II. megoldás) KöMaL, 60. kötet (1980) 39. o.

[11]	(1688. feladat) KöMaL, 63. kötet (1981) 91. o.

[12]	(701. feladat) KöMaL, 36. kötet (1966) 138. o.

[13]	Nagy László: Merev testek síkmozgása. Műszaki Könyvkiadó, Budapest, 1984. 84‐85. o.

[14]	(1553. feladat) KöMaL, 59. kötet (1979) 183. o.

[15]	(1885. feladat) KöMaL, 67. kötet (1983) 192. o.

[16]	KöMaL, 43. évf. (1993) 177. o.

[17]	(OKTV 1977. évi II/1. feladat) KöMaL, 55. kötet (1977) 83. o.

[18]	(1061. feladat) KöMaL, 46. kötet (1973) 39. o.

[19]	Szvetnik Endre: Szakdolgozat, JATE (1984.)

^{$^{*}$}Az 1992. decemberi Téli Ifjúsági Fizikai Ankéton elhangzott előadás rövidített változata.

^{$^{*}$}A mozgás síkjára merőleges forgástengelyeket az ábrákon egy-egy ponttal fogjuk jelölni.

^{$^{*}$}A pillanatnyi forgástengely a test zérus sebességű pontján átmenő tengelyt jelenti. Általában érdemes a testhez rögzített, vele együtt mozgó sík egészét vizsgálni, hiszen nem biztos, hogy a zérus sebességű pont a testre esik. A továbbiakban a "testen'' ezt az egész síkot értjük.

^{$^{*}$}A továbbiakban $A$ -val jelölöm ezt a pontot.

^{$^{*}$}A merev test bármely pontjára érvényes, hogy a haladó mozgásból és forgásból adódó gyorsulások vektori összege a nyugvó rendszerbeli gyorsulást adja.

^{$^{*}$}Ezt az esetet tárgyalja a Merev testek síkmozgása című fakultációs füzet, de az ott található bizonyítás hibás $^{[13]}$ .

^{$^{*}$}A probléma megoldása először hibásan jelent meg $^{[14]}$ , majd ismételten kitűzték $^{[15]}$ . (A feladat eredeti szövege a rezgésidőt kérdezte.)

^{$^{*}$} Ezek tanulmányozása vezette rá a Szerzőt a (3) tétel felismerésére $^{[19]}$ .