Kezdőlap


Cím:	1992. évi Eötvös-verseny
Szerző(k):	Radnai Gyula
Füzet:	1993/április, 177 - 183. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Vékonyfalú, belül üres félgömböt kétféleképpen hozunk ‐ kis kitérésű ‐ lengésbe. Egyik esetben a domború oldalán fekszik egy vízszintes asztalon, másik esetben homorú oldalával lefelé, középen egy függőleges tű hegyére támaszkodik.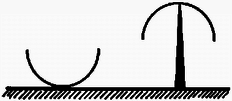

Melyik esetben lesz nagyobb a lengésidő? (A tömegközéppont mindkét esetben síkmozgást végez.)
Megoldás. Először a tű hegyére támasztott félgömb lengésidejét határozzuk meg. Ha ezt a fizikai ingát a földi nehézségi erőtérben

α

szöggel kilendítjük, akkor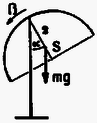

\begin{matrix} M = m g s \cdot sin α \end{matrix}

nagyságú forgatónyomaték igyekszik azt visszatéríteni. (Szokásosan

s

-sel jelöltük a tömegközéppont és a forgáspont távolságát.)

A forgástengely a tű hegyén átmenő vízszintes egyenes, ábránkon a papír síkjára merőleges. Erre a tengelyre vonatkozó tehetetlenségi nyomaték a Steiner-tétel szerint

\begin{matrix} Θ = Θ_{S} + m s^{2}, \end{matrix}

ahol

Θ_{S}

a tömegközépponton átmenő, az előbbivel párhuzamos tengelyre vonatkozó tehetetlenségi nyomatékot,

m

pedig az üres félgömb tömegét jelöli. A lengés során

Θ_{S}

nem változik meg.
A forgómozgás alapegyenlete:

M = Θ β

, esetünkben (előjelre is helyesen):

\begin{matrix} - m g s \cdot sin α = (Θ_{S} + m s^{2}) β, \end{matrix}

ahonnan a kis szögekre megengedhető

sin α \approx α

közelítéssel kapjuk:

\begin{matrix} β = \frac{m g s}{Θ_{S} + m s^{2}} \cdot α . \end{matrix}

Teljesül tehát a harmonikus torziós rezgés

β = - ω^{2} α

feltétele, és a rezgésidő kiszámítható:

\begin{matrix} T_{1} = \frac{2 π}{ω_{1}} = 2 π \sqrt[]{\frac{Θ_{S} + m s^{2}}{m g s}} . \end{matrix}

Ezek után határozzuk meg az asztalon billegő félgömb mozgásának periódusidejét! Ez az előbbinél nehezebb feladat, mivel most a testnek egyetlen pontja sem rögzített. Ilyenkor is felírhatjuk azonban a forgómozgás alapegyenletét a tömegközépponton átmenő tengelyre, annak ellenére, hogy a tömegközéppont mozog, sőt, gyorsul is. (A tömegközéppont gyorsulását a test szöggyorsulásával lehet majd kapcsolatba hozni.)
Lendítsük ki

α

szöggel a vízszintes asztalon levő üres félgömböt! A testre a következő erők hatnak:

m g

a tömegközéppontban, függőlegesen lefelé;

K

az asztal és a félgömb érintkezési pontjában, függőlegesen felfelé;

F_{s}

súrlódási erő az érintkezési pontban, vízszintesen, a kimozdulással ellentétes irányban.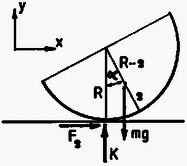

Most használjuk fel azt a megszorítást, hogy a kitérés kicsi. Minél kisebb a kitérés, annál inkább elhanyagolható a tömegközéppont emelkedése a vízszintes elmozduláshoz képest. A tömegközéppont vízszintes elmozdulása

\begin{matrix} x = - R α + (R - s) sin α \approx - R α + (R - s) α = - s α . \end{matrix}

A tömegközéppont függőleges elmozdulása

\begin{matrix} y = (R - s) - (R - s) cos α = (R - s) (1 - cos α) \approx 0 \end{matrix}

(Pontosabban is fogalmazhatunk: Míg

x

a kicsiny

α

-val arányosan elsőrendűen kicsiny, addig az

y

emelkedés

α^{2}

-tel arányos, ún. másodrendűen kicsiny mennyiség.)
Az elmozdulásokból a sebességekre, majd a gyorsulásokra következtethetünk. A tömegközéppont gyorsulása a fentiek szerint

\begin{matrix} a_{x} = - s \cdot β, \\ a_{y} = 0. \end{matrix}

Vízszintes irányban a súrlódási erő gyorsít: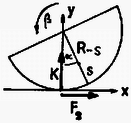

\begin{matrix} F_{s} = m \cdot a_{x} = - m s β . \end{matrix}

Függőlegesen

K

és

m g

egyensúlyt tartanak (hiszen

a_{y} = 0

\begin{matrix} K = m g . \end{matrix}

Végül pedig felírhatjuk a forgómozgás alapegyenletét a tömegközépponton átmenő vízszintes tengelyre:

\begin{matrix} - K (R - s) α + F_{s} \cdot s = Θ_{S} \cdot β, \end{matrix}

(az erőkarok az ábráról leolvasható közelítő értékek). Behelyettesítve az erőket

\begin{matrix} - m g (R - s) α - m s^{2} β = Θ_{S} β, \end{matrix}

ahonnan

β

kifejezhető:

\begin{matrix} β = - \frac{m g (R - s)}{Θ_{S} + m s^{2}} \cdot α . \end{matrix}

Ismét

β = - ω^{2} α

alakú összefüggést kaptunk, a mozgás tehát harmonikus rezgés, és a periódusidő

\begin{matrix} T_{2} = \frac{2 π}{ω_{2}} = 2 π \sqrt[]{\frac{Θ_{S} + m s^{2}}{m g (R - s)}} . \end{matrix}

A két rezgésidő aránya

\begin{matrix} \frac{T_{2}}{T_{1}} = \sqrt[]{\frac{s}{R - s}} . \end{matrix}

Most már csak a tömegközéppont helyzetét, vagyis

s

értékét kell meghatároznunk. Ez többféle módszerrel is lehetséges. Elegáns módszer kínálkozik, ha felhasználjuk a gömbövek egyik érdekes tulajdonságát: két párhuzamos, egymástól

Δ h ≪ R

távolságra lévő síkkal bárhogyan elmetszve egy gömbhéjat, mindig azonos felszínű gömbövet kapunk: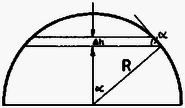

\begin{matrix} A = 2 π R sin α \cdot \frac{Δ h}{sin α}, \\ A = 2 π R \cdot Δ h = állandó. \end{matrix}

Ha tehát a vékony félgömbhéjat gondolatban összenyomjuk a szimmetriatengelyére, akkor ott egy egyenletes tömegeloszlású pálcát kapunk, amelynek tömegközéppontja a felezőpontjában van.
Ezek szerint

s = R / 2,

a rezgésidők kérdéses aránya:

\begin{matrix} \frac{T_{1}}{T_{2}} = \sqrt[]{\frac{R / 2}{R - R / 2}} = 1. \end{matrix}

A két lengésidő tehát kis kitérések esetén közelítőleg egyenlő egymással.

Megjegyzések: 1. Ha nem hanyagoljuk el a tömegközéppont emelkedését az asztalon billegő félgömb esetén, akkor erre a lengésidőre kissé nagyobb érték adódik. Így a valóságos, kísérletileg is ellenőrizhető esetben a félgömb ‐ ha azonos szögkitérésű helyzetekből indítjuk, ‐ valamivel lassabban billeg az asztallapon, mint a tű csúcsán.
2. Az

s = R / 2

összefüggés is csak közelítőleg igaz, mivel a gömbhéj vastagsága nem zérus, ‐ csak éppen elhanyagoltuk. (A jó fizikus a lényeg megragadásának és a probléma szempontjából lényegtelen dolgok elhanyagolásának művésze.)

2. feladat. Körülbelül

1 {cm}^{2}

keresztmetszetű,

80 cm

hosszú, felül nyitott üvegcsövet színültig megtöltünk higannyal. A cső felső végére ráhúzzuk és befőttesgumival a csőhöz szorítjuk egy teljesen összelappadt (levegőt nem tartalmazó) lufi száját. Ezután a csövet a levegőben tartva felfordítjuk.
Mi fog történni? (Készítsen rajzot is!)

Megoldás. Feltételezhetjük, hogy amikor ráhúzzuk az összelappadt lufit az üvegcső szájára, a higany feletti részben nem lesz levegő, és később sem tud bejutni levegő a lufi belsejébe.
Fordítsuk meg a csövet!
Függőleges helyzetben a cső ‐ most már alul levő ‐ szájánál a lufihártyára belülről

80

cm magas higanyoszlop nyomása, kívülről pedig a külső levegő nyomása hat. (Vegyük ez utóbbit

76

Hgcm-nek.)
A belső, nagyobb nyomás kissé szétnyitja az összelappadt lufit, s a higany elindul lefelé.

80 - 76 = 4 {cm}^{3}

higany lefut egészen a lufi aljára, és ekkor a folyamat leáll. A csőben marad

76

cm magas higanyoszlop, fölötte vákuum (a higanygőz nyomása elhanyagolható). Alul, a cső szájától kezdve a lufi újra összelappadt állapotban van, mert a külső légnyomás összenyomja. Legalul, az összelappadt lufiban lévő

4 {cm}^{3}

higany kicsi, kidudorodó zacskóban gyűlik össze.
A folyamat legfontosabb pillanatait az alábbi ábrasorozat szemlélteti (,,oldalnézetben"):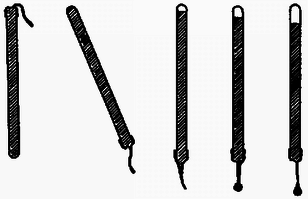

Ha túl gyorsan fordítjuk meg a csövet, esetleg a végén még meg is lökjük kissé,

4 {cm}^{3}

-nél több higany is le tud folyni a lufi aljára. Ekkor a végállapotban a külső légnyomás kissé visszanyomná a lufit a cső szájánál a cső belseje felé. Ugyanakkor a lufit a higany lefelé húzza, kissé megnyújtja a gumit, s ez a hatás a cső szájánál is érvényesül. Mindezek azonban olyan kicsiny nyomáskülönbséget és többleterőt eredményeznek, hogy a lufinak ebből származó alakváltozása szabad szemmel alig vehető észre, s a megoldást lényegesen nem módosítja.
3. feladat. Két egyforma szigetelő-tartón két egyforma fémgömb nyugszik egymás közelében. Töltés egyiken sincs. Egy néhány száz voltos telep egyik sarkát leföldeljük, a másik sarokhoz csatlakozó vezeték végével pedig megérintjük először az egyik (mondjuk a bal oldali), azután a másik (jobb oldali) gömböt, majd a telepet eltávolítjuk. Ezután felülről, szigetelő fonálon, kicsiny, töltetlen golyócskát engedünk le a két gömb közé, lehetőleg pontosan középre.
Mit tapasztalunk?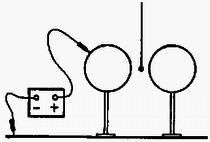

Megoldás. Első tekintetre úgy tűnik, hogy semmi különbség nincs a két gömb feltöltése között. Mindkét gömb töltetlen, azonos sugarú, s a földtől is ugyanakkora távolságra vannak. A megoldás kulcsa mégis az, hogy észrevegyük: más-más ,,környezetben'' történik a feltöltés. Amikor az első gömböt töltjük fel, egy töltetlen gömb áll közben mellette. Amikor a másodikat töltjük, amellett már egy töltött gömb áll!
Jelöljük

Q_{1}

-gyel azt a töltést, amelyet egy magános gömb venne fel a telepből.
Az első gömb feltöltésekor

Q_{1}

-nél nagyobb, mondjuk

Q_{1} + Q_{2}

töltés áramlik erre a gömbre, mert a mellette álló töltetlen gömbön elektromos megosztás történik, s ez leköt a gömbön

Q_{2}

töltést.
A második gömbre

Q_{1}

-nél kisebb, mondjuk

Q_{1} - Q_{3}

töltés vihető fel ugyanarról a telepről, mert emellett már egy ugyanilyen előjelű töltéssel feltöltött gömb áll.
Könnyebben áttekinthető és kvantitatívan is tárgyalható a probléma, ha bevezetjük a gömböknek mind a földhöz, mind egymáshoz képesti kapacitásait.
Jelöljük

C_{1}

-gyel egy gömb és a föld közötti,

C_{2}

-vel pedig a két gömb közötti kapacitást (ld. 1. ábra).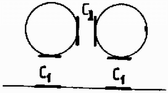

1. ábra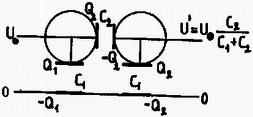

2. ábra

Az első (mondjuk a bal oldali) gömböt megérintve az

U_{0}

feszültségű telep pozitív sarkához csatlakozó vezeték végével, a 2. ábrán látható elektromos állapot fog kialakulni. (A feltüntetett ‐ fiktív ‐ vezetékek megkönnyítik a kapcsolás felismerését.)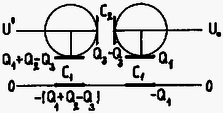

3. ábra

Mindkét gömb ekvipotenciális, de a jobb oldali gömb potenciálja kisebb. Ez ugyanis

\begin{matrix} U^{'} = \frac{Q_{2}}{C_{1}}, \end{matrix}

míg a bal oldali gömbre:

\begin{matrix} U_{0} = \frac{Q_{1}}{C_{1}} = \frac{Q_{2}}{C_{2}} + \frac{Q_{2}}{C_{1}} . \end{matrix}

Innen az alábbi összefüggések adódnak:

\begin{matrix} Q_{2} = Q_{1} \frac{C_{2}}{C_{1} + C_{2}}, illetve U^{'} = U_{0} \frac{C_{2}}{C_{1} + C_{2}} . \end{matrix}

A bal oldali gömbre összesen

\begin{matrix} Q_{1} + Q_{2} = Q_{1} (1 + \frac{C_{2}}{C_{1} + C_{2}}) \end{matrix}

nagyságú töltés kerül.
Ezek után érintjük hozzá a telep pozitív sarkáról jövő vezeték végét a jobb oldali gömbhöz. Ennek potenciálja

U_{0}

lesz, felmegy rá

Q_{1} - Q_{3}

töltés;

Q_{1}

a föld felé, ‐

Q_{3}

a másik gömb felé, s így a 3. ábrán látható elektromos állapot alakul ki.
Most is felírható az

U_{0}

feszültség kétféle módon:

\begin{matrix} U_{0} = \frac{Q_{1}}{C_{1}} = \frac{- Q_{3}}{C_{2}} + \frac{Q_{1} + Q_{2} - Q_{3}}{C_{1}} . \end{matrix}

Innen pedig a következő összefüggésekhez jutunk:

\begin{matrix} Q_{3} = Q_{1} {(\frac{C_{2}}{C_{1} + C_{2}})}^{2}, illetve U^{''} = U_{0} (1 + \frac{C_{1} C_{2}}{{(C_{1} + C_{2})}^{2}}), \end{matrix}

mivel

U^{''} = \frac{Q_{1} + Q_{2} - Q_{3}}{C_{1}} .

A jobb oldali gömb töltése végül:

\begin{matrix} Q_{1} - Q_{3} = Q_{1} [1 - {(\frac{C_{2}}{C_{1} + C_{2}})}^{2}] . \end{matrix}

A két gömb töltéseinek aránya:

\begin{matrix} \frac{Q_{1} - Q_{3}}{Q_{1} + Q_{2}} = 1 - \frac{C_{2}}{C_{1} + C_{2}} = \frac{C_{1}}{C_{1} + C_{2}} < 1. \end{matrix}

Ha felülről, szigetelő fonálon, kicsiny, töltetlen golyócskát engedünk le a két gömb közé, lehetőleg pontosan középre, akkor ez a golyócska az ottani térerősség hatására dipóllá válik (akár szigetelő, akár vezető, csak a mechanizmus más), és a nagyobb töltésű gömb maga felé húzza.
A golyócska kilendül, balra.

Megjegyzés.

U^{''} > U_{0}

, vagyis a bal oldali gömb földhöz képesti feszültsége nagyobb lesz, mint a telepé! Ha pl.

\frac{C_{2}}{C_{1} + C_{2}} = \frac{1}{10}

és

U_{0} = 3000

V, akkor

U^{'} = 300

U^{''} = 3270

V. A bal oldali gömb töltése

1, 10 \cdot Q_{1}

, a jobb oldalié

0, 99 \cdot Q_{1}

lesz az adott esetben.

A verseny végeredménye

A Versenybizottság a beérkezett 246 dolgozat körültekintő átvizsgálása és értékelése alapján egyhangúlag megállapította, hogy Katz Sándor dolgozata kiemelkedik a mezőnyből. Egyedül ő oldotta meg hibátlanul mindhárom feladatot, az első példára adott energetikai megoldása különösen értékes. Ezért
I. díjat kapott KATZ SÁNDOR, a bonyhádi Petőfi Sándor Evangélikus Gimnázium IV. osztályos tanulója, JURISITS JÓZSEF és ERDÉLYESI JÁNOS tanítványa. Pénzjutalma 8 000 Ft.

A II. díjat a Versenybizottság nem adta ki.

III. díjat kapott és a verseny 2-10. helyezettje lett egyenlő helyezésben a következő kilenc versenyző:

DORNBACH PÉTER, az ELTE Apáczai Csere János Gyakorló Gimnáziumának IV. oszt. tanulója, FLÓRIK GYÖRGY tanítványa;
GEFFERTH ANDRÁS, a Fazekas Mihály Fővárosi Gyakorló Gimnázium IV. oszt. tanulója, HORVÁTH GÁBOR tanítványa;
MORVAI PÉTER, a Fazekas Mihály Fővárosi Gyakorló Gimnázium III. oszt. tanulója, HORVÁTH GÁBOR tanítványa;
MAULIS ÁDÁM, az ELTE I. éves matematika-fizika tanárszakos hallgatója, aki a budapesti Széchenyi István Gimnáziumban érettségizett, mint DRASKÓCZY PÁL és INGES JÁNOS tanítványa;
PAPP ZSOMBOR, a zalaegerszegi Zrínyi Miklós Gimnázium IV. oszt. tanulója, VADVÁRI TIBOR tanítványa;
PÁLFALVI LÁSZLÓ, a pécsi Apáczai Csere János Gimnázium III. oszt. tanulója, KECZER ZOLTÁN tanítványa;
SOMOGYVÁRI ZOLTÁN, az ELTE Radnóti Miklós Gyakorló Gimnázium IV. oszt. tanulója, TOMCSÁNYI PÉTER tanítványa;
TÓTH GÁBOR, az Újpesti Műszaki Középiskola 5. oszt. tanulója, valamint
VEISZ LÁSZLÓ, az ELTE I. éves fizikus hallgatója, aki a budapesti Budai Nagy Antal Gimnáziumban érettségizett, mint TÓTH CSABA tanítványa.
A III. díjat kapott versenyzők pénzjutalma egyenként 2000 Ft.

Dicséretet és egyenként 1000 Ft pénzjutalmat kapott az alábbi négy versenyző:

PAFKA SZILÁRD, az ELTE I. éves fizikus hallgatója, aki Romániában, a borosjenői gimnáziumban (Líceum Teoretic, Ineu) érettségizett, mint OTMAR HUHN tanítványa;
PROHÁSZKA ZOLTÁN, a budapesti Veres Pálné Gimnázium III. oszt. tanulója, OPORNÉ FODOR MÁRIA tanítványa;
SZÉKELY SÁNDOR, a kecskeméti Katona József Gimnázium IV. oszt. tanulója, NÉMETH ÁGNES tanítványa, és
VERES GÁBOR, a balassagyarmati Balassi Bálint Gimnázium IV. oszt. tanulója, BOGNÁR MIHALYNÉ és FŰRÉSZ ISTVÁN tanítványa.

A Versenybizottság további sorrendet nem állapított meg, és ezúton is gratulál a verseny nyerteseinek.