Cím: Arcképcsarnok: Két barát (Bayer István és Gáspár Rezső)
Szerző(k):  Radnai Gyula 
Füzet: 1993/december, 462 - 465. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bayer István a Faragó-féle lapok egyik legszorgalmasabb megoldója volt.
Később Eötvös kollégistaként elvégezte az egyetem matematika-fizika tanár szakát, s tanár lett ő is akárcsak édesapja. Az Eötvös Kollégiumban Bakos Tiborral került egy szobába, akit a Lapokból már névről ismert. Bakos Tibor Szombathelyről jött, tanára Radványi László volt, aki később a budapesti Mátyás Király gimnáziumban Schweitzer Miklóst is tanította, Schweitzer Miklós 1941-ben az Eötvös-versenyen díjat nyert. (Ma Schweitzer Miklósról van elnevezve az egyetemisták legnehezebb matematika versenye.)
Az egyetemet elvégezve, a két barát messze került egymástól, de kapcsolatuk se egymással, se Faragó Andorral nem szakadt meg, most már mint feladat-kitűzők segítettek a szerkesztőnek. Bayer István ma is őrzi Faragó Andornak hozzá írt levelét:

 
 

A dokumentum azért is értékes, mert Faragó Andor kézírását és aláírását őrzi.
Bayer István később az Országos Pedagógiai Intézetben lett a fizika tanszék vezetője, a fizikaoktatás érdekében végzett munkásságáért 1958-ban Kossuth-díjat kapott.
Az egyik érdekes, nem túl nehéz feladat, melyet Bayer Istvántól 1937-ben ‐ 12 évvel az előbbi levél megírása után ‐ közölt Faragó Andor, a következő:
 

1130. Robogó vonaton hány mp-ig kell számolnunk a kattogásokat, l méter sínhosszúság esetén, hogy azoknak a száma a vonat c sebességét adja
(  km  óra-ban)?
 
Pl. l=6, 8, 12, 18, 24.
Bayer.
 

I. Megoldás: Egy óra alatt a vonat megtesz c km-t, azaz 1000c m-t ; ezalatt a kattogások száma 1000cl. Egy mp alatt 1000c3600l és x mp alatt 1000cx3600l a kattogások száma. Már most x úgy határozandó meg, hogy a kattogások száma c legyen, tehát
1000cx3600l=cés innenx=3.6l.
l adott értékei mellett a keresett idő 21.6, 28.8, 43.2, 64.8, 86.4 mp.
Fővonalon általában 12 m-esek a sínek, újabban helyenként már 24 m-esek. Igy pl. a 43.2 mp alatti kattogások száma megadja a vonat sebességét kmora - ban.
Erőd Márta (Koháry István rg. V. o. Gyöngyös.)

 

Megoldották.: Bagdy D., Bleyer J., Bleyer L., Dalmy Gy., Danciger E., Dudás I., Elek Gy., Erdősi N., Fehérváry Á., Füleky L., Gaál A., Grósz L., Halász I., Havas I., Jakab K., Klein J., Kovalóczy Gy., Mikla B., Steiner I. Tornai J., Tóth B., Vásárhelyi Nagy S., Wiczay I., Zlehovszky K.
 

A mai diák számára is érdekes információ, ami ebből a példából kiolvasható, hogy akkor bizony még nem lehetett a síneket összehegeszteni. Bayer István egy diákkori megoldása:
 

12. Szilárd O ponthoz erősített két (elhanyagolható súlyú) fonál ‐ OA=1 m, OB=3 m ‐ A és B végpontjához AB=2 m hosszú, 10 kg súlyú homogén rúd van erősítve. Állapítsuk meg e rúd egyensúlyi helyzetét! Ebben a helyzetben mekkora erő feszíti ki az OA, ill. OB fonalat ? Mekkora P súlyt kell A pontba helyezni, hogy ezáltal a rúd vízszintes helyzetbe kerüljön?
Megoldás: 1∘ A rúd egyensúlyban van, ha súlypontja O ponton átmenő függélyesbe esik.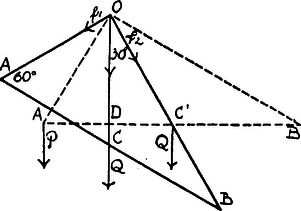
 
 

Az AOB▵ derékszögű O-nál, mert 12+(3)2=22. Hegyesszöge 30∘, ill. 60∘. Az AB rúd súlypontja C, az AB felezőpontja. OC=AC=OA=1 m. Egyensúly esetén OA a vízszintessel 30∘-ú szöget zár be.
2∘ Ha a rúd súlyának támadó pontját O -ba helyezzük, ezt az erőt két összetevőre bontjuk OA, ill. OB irányban. ,
OA irányában f1=10⋅cos60∘=102=5 kg
OB irányában f2=10⋅cos30∘=1032=53=8.66 kg.
3∘ Ha azt akarjuk, hogy a rúd vízszintes helyzetbe kerüljön, P súlynak és a rúd súlyának O pontra vonatkozólag egyenlő forgató nyomatékkal kell bírnia. Ha a rúd vízszintes helyzetben van, C pont C'-be kerül és az O ponton átmenő függélyes AC'-t felezi, mert AOC'▵ egyenlő oldalú. Tehát, hogy a vízszintes egyensúlyi helyzet létrejöjjön, kell, hogy P⋅AD=10⋅C'D legyen ; mivel pedig AD=C'D,P=10 kg.
Bayer István (kir. kath. rg. VII. o. Mezőkövesd).

Gáspár Rezső, a debreceni Tudományegyetem elméleti fizikai tanszékének későbbi vezetője. A colorádói és a göttingeni egyetemi vendégprofesszor, Bayer István tanítványa volt a pestszenterzsébeti gimnáziumban, az ő biztatására kezdte el beküldeni a feladatmegoldásokat, a Lapokhoz.
 
 

Most egy olyan feladatra adott tömör megoldását közöljük, amelyet már Arany Dániel is kitűzött, mégpedig az első évfolyam első számában. Ez volt a legelső fizika feladat a Lapokban. Idézzük először az Arany Dániel féle kitűzést és megoldást, majd Gáspár Rezső megoldását 43 évvel későbbről:
 

13. Az M pontot összekötöm az ABC háromszög csúcspontjaival. Mutassuk meg, hogy az MA,MB és MC erők eredője keresztülmegy a háromszög súlypontján, G-n, és egyenlő 3MG-vel.
 

Szerkesszük meg az MB=QésMC=R erők eredőjét, P'-t. Ezen erő felezi a háromszögnek BC oldalát a D pontban, és nagysága, ME=2MD-vel. A P és P' erők eredője S, felezi az AE egyenest az F pontban, és nagysága MH=2MF-fel. Az S eredő tehát keresztülmegy az AME  háromszög súlypontján, G-n, mely pont az AD egyenesen az A-tól 23AD távolságra fekszik. De ezen G pont, ez utóbbi tulajdonságánál fogva egyszersmind az ABC háromszög súlypontja is. A feladatban foglalt kijelentések közül az első ezzel igazolva van. Másrészt a G az MF egyenesen az M ponttól MG=23MF=13MH távolságra van. Tehát MH=3MG-vel, ami még bebizonyítandó volt.
 

623. Az ABC▵ síkjában fekvő M pontra az MA→,MB→,MC→ erők hatnak. Mutassuk meg, hogy ezen három erő eredője az ABC▵ S súlypontján megy keresztül és nagyságra nézve 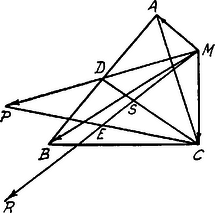=3MS.
 
 

I. Megoldás. Szerkesszük meg előbb két erő eredőjét, pl. MA→ és MB→ erőkét. Ezen erők parallelogrammjának egyik átlója AB; a második átló, a két erő eredője AB felezőpontján, D-n megy keresztül és ezen eredő: MP→, nagyságra nézve =2MD.
 
Az MP→ és MC→ erők eredője MR→ ugyancsak felezi a CP távolságot, az E pontban: MR=2ME.
Az MPC▵-ben CD és ME súlyvonalak meghatározzák MPC▵ súlypontját S-t, úgy hogy CS=2SD. Azonban CD az ABC▵-nek is súlyvonala és a rajtafekvő S pont az ABC▵ - nek is súlypontja. Eszerint MR→ valóban keresztülmegy az ABC▵ súlypontján és
MR→=2ME=2⋅32MS=3MS→.

Destek Miklós(kegyesrendig.VIII.o.Bp.)

 

Megoldották : Fehér Gy., Grosz L., Komlós J., Nagy E., Petricskó M., Sándor Gy., Schreiber B., Sebestyén Gy., Tóbiás I., Steiner G., Weisz A.
 

Jegyzet. Ezen tétel speciális esete a 612. feladatban szereplő általánosabbnak. (L. XIV. évf. 1. sz. 22. o.)
 

II. Megoldás. A vektorok összetételének szabálya szerint érvényes:
MA→=MS→+SA→,MB→=MS→+SB→,MC→=MS→+SC,→
tehátMA→+MB→+MC→=3MS→+(SA→+SB→+SC→).
AzonbanSA→+SB→+SC→=0
és ígyMA→+MB→+MC→=3MS.→

Gáspár Rezső (Kossuth Lajos g. VIII. o. Pestszenterzsébet).

 

Jegyzet. Nehány megoldás a vektorok összetételének szabályát helytelenül alkalmazta és így eredményül 3SM→ állott elő.
 

Gáspár Rezső a Magyar Tudományos Akadémia tagja. 1965-ben a kvantum kémia területén elért eredményeiért Állami-díjat kapott. Fia, ifjabb Gáspár Rezső 1959-től volt eredményes megoldója a lapoknak.