Cím:	Érdekességek a négyzetgyök 2-ről
Szerző(k):	Poros Tibor
Füzet:	1993/november, 349 - 356. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. Geometriai megközelítés   Az irracionális szám a pitagoreusok felfedezése. A problémához geometriai úton jutottak el. Egy szakasz mérőszámának megállapítására bármely nála nem nagyobb hosszegység választható, amely valahányszor ráfér maradék nélkül. Kérdés, hogy bármely két szakaszhoz létezik-e olyan hosszegység, amellyel mindkettő mérhető. Két szakasz esetén egy közös mértéket úgy kaphatunk meg, hogy a kisebb szakaszt felmérjük a nagyobb szakaszra, és ha a kisebb szakasz többszöröse maradék nélkül rámérhető a nagyobb szakaszra, akkor ez egy közös mérték, ha nem, akkor a maradékot felmérjük a kisebb szakaszra ‐ hasonlóan, mint előbb. Az eljárást tovább folytatva az utolsó nem nulla maradék lesz egy közös mérték. Előfordulhat azonban, hogy az előző eljárás soha nem ér véget. Ekkor a görögök azt mondták, hogy a két szakasz összemérhetetlen. Ha a két szakasz közül az egyiknek van mérőszáma, akkor a másiké arrheton (kimondhatatlan) szám; irracionális szám. A négyzet oldala és átlója ilyen, összemérhetetlen. 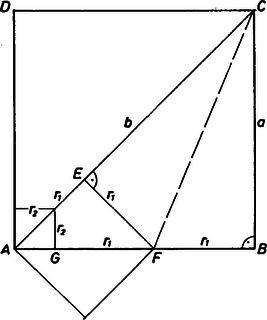    Legyen a négyzet oldala $a$, a négyzet átlója $b$. A háromszög-egyenlőtlenségből következik, hogy $b<2a\mathrm{,}$ továbbá látható, hogy $b>a\mathrm{.}$ Tehát $\begin{array}{c}{\displaystyle b=a+r_1\mathrm{.}}\end{array}$ (1) Állítsunk merőlegest az átlóra $E$-ben, ahol $\overline{EC}=a\mathrm{.}$ Az $EFC△$ és az $FBC△$ egybevágóak ‐ két oldal és a nagyobbikkal szemben fekvő szög megegyezik. Így $\overline{EF}=\overline{FB}\mathrm{.}$ Az $EFA\sphericalangle$ ${45}^{\circ }$-os, ebből következik, hogy $r_1=\overline{EF}=\overline{FB}\mathrm{.}$ Most mérjük fel $r_1$-et $\overline{AF}$-re $F$-ből. Ezzel a négyzet oldalát az átlójára mérjük fel. Az ábráról jól látható, hogy $\begin{array}{c}{\displaystyle a=2r_1+r_2\mathrm{.}}\end{array}$ (2) Ha az eljárást folytatjuk ‐ $G$-ben állítva merőlegest, azt tapasztaljuk, hogy következő lépésként ismét egy négyzet oldalát mérjük fel átlójára. Az eljárás ezért soha nem ér véget. Az is jól látható, hogy a lépések ismétlődnek, így $\begin{array}{c}{\displaystyle r_1=2r_2+r_3\mathrm{,}}\end{array}$ (3) általánosan $\begin{array}{c}{\displaystyle r_n=2r_{n+1}+r_{n+2}\mathrm{.}}\end{array}$ Azt tudjuk, hogy a maradékok ‐ $\left(r_i\right)$ ‐ szigorúan monoton csökkenő sorozatot alkotnak, ez az algoritmus következménye. Az is könnyen belátható, hogy a maradékok lassan ,,elfogynak'', a maradékokból álló $\left(r_i\right)$ sorozat határértéke nulla. Tegyük fel ugyanis, hogy létezik olyan ${\epsilon }_0>\mathrm{0,}$ hogy az $\left(r_i\right)$ sorozatnak végtelen sok eleme nagyobb, mint ${\epsilon }_0\mathrm{.}$ Azt tudjuk, hogy $b=a+r_1=a+2r_2+r_3=a+2r_2+2r_4+r_5\mathrm{,}$ és az eljárást folytatva $b$ felírható a páros indexű maradékok segítségével: $\begin{array}{c}{\displaystyle b=a+2\left(r_2+r_4+r_6+\text{...}+r_{2i}+\text{...}\right)\mathrm{.}}\end{array}$ Hasonlóan $b=r_1+2\left(r_1+r_3+\text{...}+r_{2i+1}+\text{...}\right)$ a páratlan indexű maradékokkal. Összeadva e két összefüggést kapjuk, hogy $2b=a+r_1+2\left(r_1+r_2+r_3+\text{...}\right)\mathrm{,}$ ebből pedig következik, hogy $2b>2\left(r_1+r_2+r_3+\text{...}\right)\mathrm{,}$ azaz $b>\sum _{i=1}^{\infty }{r}_i$. Mivel végtelen sok ${\epsilon }_0$-nál nagyobb maradék van, ezért $\left(\left[\frac{b}{{\epsilon }_0}\right]+1\right)=n$ darab ${\epsilon }_0$-nál nagyobb maradék is van. Tehát $$\begin{gathered} \begin{array}{c}{\displaystyle b>\sum _{i=1}^{\infty }{r}_i>\sum _{k=1 \\ {r}_{1k}>{\epsilon }_0>0}^n{r}_{1k}>\left(\frac{b}{{\epsilon }_0}+1\right){\epsilon }_0>b\mathrm{.}}\end{array} \end{gathered}$$ Ellentmondásra jutottunk, tehát a maradékokból álló sorozat nullához tart. Vegyük észre, hogy ha fel tudnánk $b$-t $a$ és $r$ törtrészei segítségével írni úgy, hogy az összeg a maradékok közül egy lehetőleg minél kisebb tagot tartalmazzon, akkor $a=1$ (egységnyi hosszúságú szakasz) választása esetén $b=\sqrt[]{2}$ értékét tetszőleges pontossággal meghatározhatnánk. A (2) összefüggésből $r_1=\frac{a}{2}-\frac{r_2}{2}$, ezt visszaírva (1)-be $b=a+\frac{a}{2}-\frac{r_2}{2}$ adódik. (3)-ból $\frac{r_1-r_3}{2}=r_2$, és mivel $r_1=\frac{a-r_2}{2}$, így $\frac{\frac{a-r_2}{2}-r_3}{2}=r_2\mathrm{,}$ azaz $\frac{a-2r_3}{5}=r_2\mathrm{.}$ Ha ezt beírjuk a $b$-re kapott utolsó egyenletbe, $b=a+\frac{a}{2}-\frac{a}{10}+\frac{r_5}{5}$ adódik. Mivel $\frac{r_2-r_4}{2}=r_3$, így $\frac{\frac{a-2r_3}{5}-r_4}{2}=r_3$, tehát $\frac{a-5r_4}{12}=r_3\mathrm{.}$ Ezt visszaírva a $b$-re kapott utolsó egyenletbe, kapjuk: $\begin{array}{c}{\displaystyle b=a+\frac{a}{2}-\frac{a}{10}+\frac{a}{60}-\frac{r_4}{12}\mathrm{.}}\end{array}$ Hasonlóan kapjuk: $b=a+\frac{a}{2}-\frac{a}{10}+\frac{a}{60}-\frac{a}{348}+\frac{r_5}{29}\mathrm{.}$   $a=1$ esetén $b=\sqrt[]{2}\approx 1\mathrm{,}41437$ adódik az előző összefüggésből.   Az eljárást folytatva $b=a+\frac{a}{2}-\frac{a}{10}+\frac{a}{60}-\frac{a}{348}+\frac{a}{2030}-\frac{r_6}{70}$ adódik, és $a=1$ esetén $b=\sqrt[]{2}\approx 1\mathrm{,}4142$. Legyen $b\left(1\right)=a+\frac{r_1}{c_1}$ az összeg első, $b\left(2\right)=a+\frac{a}{c_1{c}_2}-\frac{r_2}{c_2}$ a második alakja. Legyen $c_0=\mathrm{0,}{c}_1=\mathrm{1,}{c}_2=\mathrm{2,}{c}_3=\mathrm{5,}\text{...}\mathrm{,}{c}_i=2c_{i-1}+c_{i-2}$ $(i>1$ esetén). Azt állítjuk, hogy ‐ minden $n$-re ‐ $b$ $\begin{array}{c}{\displaystyle a+\frac{a}{c_1{c}_2}-\frac{a}{c_2{c}_3}+\text{...}+{\left(-1\right)}^n\frac{a}{c_{n-1}{c}_n}+{\left(-1\right)}^{n+1}\frac{r_n}{c_n}}\end{array}$ (4) alakban írható. Először belátjuk, hogy $r_i=\frac{a-c_i{r}_{i+1}}{c_{i+1}}\mathrm{.}$ Bizonyítás teljes indukcióval: $\begin{array}{c}{\displaystyle i=1\text{ esetén }{r}_1=\frac{a-r_2}{2}\mathrm{,}i=2\text{ esetén }{r}_2=\frac{a-2r_3}{5}\mathrm{.}}\end{array}$ Tegyük föl, hogy $n$-re teljesül, hogy $r_n=\frac{a-c_n{r}_{n+1}}{c_{n+1}}\mathrm{.}$ Ezt az $r_{n+1}=\frac{r_n-r_{n+2}}{2}$ összefüggésbe beírva $\begin{array}{c}{\displaystyle \frac{a-c_n{r}_{n+1}}{c_{n+1}}-\frac{c_{n+1}}{c_{n+1}}{r}_{n+2}=2r_{n+1}}\end{array}$ adódik, amit rendezve a kívánt $\begin{array}{c}{\displaystyle \frac{a-c_{n+1}{r}_{n+2}}{c_{n+2}}=r_{n+1}}\end{array}$ alakra hozhatunk $c_{n+2}=2c_{n+1}+c_n$ felhasználásával. Visszatérve (4)-re, azt is teljes indukcióval bizonyítjuk: $n=1$-re $b=a+\frac{r_1}{c_1}=a+r_1;n=2$-re $b=a+\frac{a}{c_1{c}_2}-\frac{r_2}{c_2}=a+\frac{a}{2}-\frac{r_2}{2}$. Tegyük föl, hogy valamilyen $n$-re $b=a+\text{...}+{\left(-1\right)}^{n+1}\frac{r_n}{c_n};$ ekkor ${\displaystyle \begin{array}{c}\hfill {\displaystyle b=a+\text{...}+{\left(-1\right)}^{n+1}\left(\frac{a-c_n{r}_{n+1}}{c_{n+1}}\right)\cdot \frac{1}{c_n}=}\hfill \\ \hfill {\displaystyle =a+\text{...}+{\left(-1\right)}^{n+1}\frac{a}{c_n\cdot c_{n+1}}+{\left(-1\right)}^{n+2}\frac{r_{n+1}}{c_{n+1}}\mathrm{.}}\hfill \end{array}}$ Mivel a maradékokból álló sorozat nullához tart, ezért $\begin{array}{c}{\displaystyle \underset{i\to \infty }{\overset{}{\text{lim}}}\left(1+\frac{1}{c_1{c}_2}-\frac{1}{c_2{c}_3}+\text{...}+{\left(-1\right)}^i\frac{1}{c_{i-1}{c}_i}\right)=\sqrt[]{2}\mathrm{.}}\end{array}$ Az előző összeg segítségével: $\begin{array}{c}{\displaystyle \sqrt[]{2}=1+\frac{1}{2}-\frac{1}{10}+\frac{1}{60}-\frac{1}{348}+\frac{1}{2030}+\text{...}}\end{array}$   2. A $c_i=2c_{i-1}+c_{i-2}$ rekurzió   A $\left(c_i\right)$ sorozat elemeit a $c_i=c_{i-2}+2c_{i-1}$ rekurziós formula adja meg, ha $i>2$, $c_1$ és $c_2$ pedig legyen $0$, illetve $1$. A Fibonacci-számokhoz hasonlóan lehetőség van a sorozat elemeit explicite is megadni, azaz $i$ ismeretében a $c_i$-t meghatározni. 1. módszer: A sorozat elemeit két mértani sorozat összegeként írjuk fel. Olyan mértani sorozatokat tekintünk, amelyek maguk is kielégítik a $c_i=2c_{i-1}+c_{i-2}$ rekurziót. Legyen $c_i=q^i\mathrm{,}q\ne 0$. Ekkor $q^i=2q^{i-1}+q^{i-2}$ minden $i⩾2$ esetén, ami $q^{i-2}$-vel való osztás miatt ekvivalens a $q^2=1+2q$ feltétellel. $q_{\mathrm{1,2}}=1\pm \sqrt[]{2}$ kielégítik az utóbbi egyenletet.   Legyen $S_1=\left(\mathrm{1,}{q}_1\mathrm{,}{q}_1^2\mathrm{,}{q}_1^3\mathrm{,}\text{...}\right)$ és $S_2=\left(\mathrm{1,}{q}_2\mathrm{,}{q}_2^2\mathrm{,}{q}_2^3\mathrm{,}\text{...}\right)$. A sorozatunkat ${\lambda }_1{S}_1+{\lambda }_2{S}_2$ alakban keressük: $\begin{array}{c}{\displaystyle \left(\mathrm{0,1,2,5,}\text{...}\right)={\lambda }_1\left(\mathrm{1,}{q}_1\mathrm{,}{q}_1^2\mathrm{,}{q}_1^3\mathrm{,}\text{...}\right)+{\lambda }_2\left(\mathrm{1,}{q}_2\mathrm{,}{q}_2^2\mathrm{,}{q}_2^3\mathrm{,}\text{...}\right)\mathrm{.}}\end{array}$ Az egyenlőség teljesüléséhez szükséges és elégséges az első 2 tag egyenlősége, hiszen mindkét oldal kielégíti a $c_i=2c_{i-1}+c_{i-2}$ rekurziót. Azaz ${\lambda }_1+{\lambda }_2=0$ és ${\lambda }_1{q}_1+{\lambda }_2{q}_2=1$-nek teljesülnie kell. Az egyenletrendszert megoldva ${\lambda }_1=\frac{1}{2\sqrt[]{2}}\mathrm{,}{\lambda }_2=-\frac{1}{2\sqrt[]{2}}$ adódik. Így ${\displaystyle \begin{array}{cc}{\displaystyle \left(\mathrm{0,1,2,5,}\text{...}\right)=\frac{1}{2\sqrt[]{2}}\left(\mathrm{1,1}+\sqrt[]{2}\mathrm{,}{\left(1+\sqrt[]{2}\right)}^2\mathrm{,}{\left(1+\sqrt[]{2}\right)}^3\mathrm{,}\text{...}\right)-}\hfill & \hfill {\displaystyle }\\ {\displaystyle }\hfill & \hfill {\displaystyle -\frac{1}{2\sqrt[]{2}}\left(\mathrm{1,1}-\sqrt[]{2}\mathrm{,}{\left(1-\sqrt[]{2}\right)}^2\mathrm{,}{\left(1-\sqrt[]{2}\right)}^3\mathrm{,}\text{...}\right)\mathrm{,}}\end{array}}$ vagyis $\begin{array}{c}{\displaystyle c_n=\frac{1}{2\sqrt[]{2}}\left({\left(1+\sqrt[]{2}\right)}^n-{\left(1-\sqrt[]{2}\right)}^n\right)\mathrm{.}}\end{array}$ 2. módszer: Tekintsük az $F\left(x\right)={\sum }_{i=0}^{\infty }{c}_i{x}^i$ ún. hatványsort. Ez ,,elég kis'' $x$ értékekre konvergens, és belátható, hogy hasonlóan számolhatunk vele, mint véges összegekkel. A $c_i=2c_{i-1}+c_{i-2}$ tulajdonság felhasználásával tekintsük ($x^2+2x-1)\cdot F\left(x\right)$-et: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle F\left(x\right)={\sum }_{i=0}^{\infty }{c}_i{x}^i}\hfill & \text{(<mo>‐</mo>)}\\ \hfill {\displaystyle 2x\cdot F\left(x\right)=2{\sum }_{i=1}^{\infty }{c}_{i-1}{x}^i}\hfill & \text{(<mo stretchy="false">+</mo>)}\\ \hfill {\displaystyle x^2\cdot F\left(x\right)={\sum }_{i=2}^{\infty }{c}_{i-2}{x}^i}\hfill & \text{(<mo stretchy="false">+</mo>)}\end{array}}$ Innen $\begin{array}{c}{\displaystyle \sum _{i=2}^{\infty }\underset{0}{\overset{}{\underbrace{\left(-c_i+2c_{i-1}+c_{i-2}\right)}}}{x}^i+\underset{0}{\overset{}{\underbrace{2c_{0}x}}}-\underset{0}{\overset{}{\underbrace{c_0}}}-\underset{-x}{\overset{}{\underbrace{c_{1}x}}}=\left(2x+x^2-1\right)F\left(x\right)\mathrm{.}}\end{array}$ Az előző összefüggésből $\begin{array}{c}{\displaystyle F\left(x\right)=\frac{-x}{x^2+2x-1}=-x\left(\frac{1}{\left(x-\left(-1-\sqrt[]{2}\right)\right)\cdot \left(x-\left(-1+\sqrt[]{2}\right)\right)}\right)\mathrm{.}}\end{array}$ Az $\frac{1}{\left(x-\alpha \right)\left(x-\beta \right)}$ tört ún. parciális törtekre bontással felírható $\begin{array}{c}{\displaystyle \frac{1}{\left(x-\alpha \right)\left(x-\beta \right)}=\frac{A}{x-\alpha }+\frac{B}{x-\beta }}\end{array}$ alakban, ahol $A$ és $B$ értékét közös nevezőre hozás után a megfelelő együtthatók összehasonlításával kaphatjuk meg. Ezt végigszámolva $\begin{array}{c}{\displaystyle F\left(x\right)=\frac{\frac{1}{2\sqrt[]{2}}x}{x-\left(-1-\sqrt[]{2}\right)}+\frac{-\frac{1}{2\sqrt[]{2}}x}{x-\left(-1+\sqrt[]{2}\right)}=}\end{array}$ ${\displaystyle \begin{array}{c}{\displaystyle =\frac{\frac{1}{2\sqrt[]{2}}x-\frac{1}{2\sqrt[]{2}}\left(-1-\sqrt[]{2}\right)+\frac{1}{2\sqrt[]{2}}\left(-1-\sqrt[]{2}\right)}{x-\left(-1-\sqrt[]{2}\right)}+}\hfill \\ {\displaystyle }\hfill & \hfill {\displaystyle +\frac{-\frac{1}{2\sqrt[]{2}}x-\left(-\frac{1}{2\sqrt[]{2}}\right)\left(-1+\sqrt[]{2}\right)+\left(-\frac{1}{2\sqrt[]{2}}\right)\left(-1+\sqrt[]{2}\right)}{x-\left(-1+\sqrt[]{2}\right)}=}\\ {\displaystyle =\frac{\frac{1}{2\sqrt[]{2}}\left(x-\left(-1-\sqrt[]{2}\right)\right)+\frac{1}{2\sqrt[]{2}}\left(-1-\sqrt[]{2}\right)}{x-\left(-1-\sqrt[]{2}\right)}+}\hfill \\ {\displaystyle }\hfill & \hfill {\displaystyle +\frac{-\frac{1}{2\sqrt[]{2}}\left(x-\left(-1+\sqrt[]{2}\right)\right)+\left(-\frac{1}{2\sqrt[]{2}}\right)\left(-1+\sqrt[]{2}\right)}{x-\left(-1+\sqrt[]{2}\right)}=}\\ {\displaystyle =\frac{1}{2\sqrt[]{2}}+\frac{1}{2\sqrt[]{2}}\cdot \left(-1-\sqrt[]{2}\right)\cdot \frac{1}{x-\left(-1-\sqrt[]{2}\right)}+}\hfill \\ {\displaystyle }\hfill & \hfill {\displaystyle +\left(-\frac{1}{2\sqrt[]{2}}\right)+\left(-\frac{1}{2\sqrt[]{2}}\right)\cdot \left(-1+\sqrt[]{2}\right)\cdot \frac{1}{x-\left(-1+\sqrt[]{2}\right)}\mathrm{.}}\end{array}}$ Végül $\frac{1}{x-\alpha }$ végtelen mértani sorba fejthető: $\begin{array}{c}{\displaystyle \frac{1}{x-\alpha }=-\frac{1}{\alpha }\cdot \frac{1}{1-\frac{x}{\alpha }}=\left(-1\right)\left({\alpha }^{-1}\right)\sum _{i=0}^{\infty }\frac{x^i}{{\alpha }^i}\mathrm{.}}\end{array}$ Így ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle F\left(x\right)=}& {\displaystyle \left(-\frac{1}{2\sqrt[]{2}}\right)\cdot {\sum }_{i=0}^{\infty }{\left(1-\sqrt[]{2}\right)}^i\cdot x^i+\left(\frac{1}{2\sqrt[]{2}}\right)\cdot {\sum }_{i=0}^{\infty }{\left(1+\sqrt[]{2}\right)}^i\cdot x^i=}\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle =}& {\displaystyle {\sum }_{i=0}^{\infty }\left(\frac{{\left(1+\sqrt[]{2}\right)}^i-{\left(1-\sqrt[]{2}\right)}^i}{2\sqrt[]{2}}\right)\cdot x^i\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">vagyis</span>}{c}_i=\frac{{\left(1+\sqrt[]{2}\right)}^i-{\left(1-\sqrt[]{2}\right)}^i}{2\sqrt[]{2}}\mathrm{.}}\hfill \end{array}}$   3. Lánctörtek   $\begin{array}{c}{\displaystyle a_0+\frac{1}{a_1+\frac{1}{a_2+\frac{1}{a_3+\frac{1}{\ddots \frac{1}{a_N}}}}}}\end{array}$ A fenti kifejezést véges lánctörtnek nevezzük. Az $a_i$-k tetszőleges valós számok lehetnek. Általánosabb tárgyalás esetén a ,,számlálókban'' az 1-esek helyett más valós számok is állhatnak, azonban itt ezekkel az esetekkel nem foglalkozunk. A fenti lánctörtet rövidebben $\left[a_0\mathrm{,}{a}_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_N\right]$-nel fogjuk jelölni. Legyen $p_0=a_0\mathrm{,}{p}_1=a_1{a}_0+\mathrm{1,}{p}_n=a_n{p}_{n-1}+p_{n-2}$, ha $n>1;$ q0=1,q1=a1 és $q_n=a_n{q}_{n-1}+q_{n-2}$, ha $n>1$. Tudjuk, hogy