Kezdőlap


Cím:	Háromszögszerkesztés szögfelező szakaszokból
Szerző(k):	Reményi Gusztáv
Füzet:	1993/november, 346 - 348. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feladat. Szerkeszthető-e a háromszög, ha a szögfelező szakaszainak hossza
a) $1, 2, 2$ egység?
b) $1, 3, 3$ egység?

Szemléletesen nyilvánvaló, hogy ha a háromszög két szögfelező szakasza egyenlő, akkor a háromszög egyenlő szárú. Ennek első bizonyítása Steinertől származik, ezért a szakirodalomban Lehmus ‐Steiner-tételként szerepel. (Részletesebben l. például: Coxeter‐Greitzer: Az újra felfedezett geometria, Gondolat Könyvkiadó, Budapest, 1977. 33‐36. o.)^{$^{*}$}

1. ábra

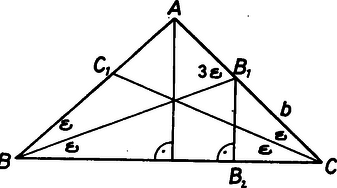
a) Tegyük fel, hogy szerkeszthető a kívánt

A B C

háromszög, akkor a Lehmus ‐ Steiner-tétel értelmében a háromszög egyenlő szárú, és a magassága 1 egység. Jelölje az alapot

B C

, a szárakat

b

, az alapon nyugvó szögeket

2 ε, B B_{1} = C C_{1} = 2

egység (1. ábra). A külső szög tétel értelmében

A B_{1} B ∢ = 3 ε

, továbbá,

B A C ∢ = π - 4 ε

. A derékszögű háromszögből

\begin{matrix} b sin 2 ε = 1. \end{matrix}

(1)

A B B_{1}

háromszögben a szinusztételből

\begin{matrix} \frac{2}{b} = \frac{sin 4 ε}{sin 3 ε} . \end{matrix}

(1)-ből a

b

-t behelyettesítve, a megszerkeszthető,

0

és

π / 4

közé eső

ε

kielégíti a

\begin{matrix} 2 sin 2 ε sin 3 ε = sin 4 ε . \end{matrix}

egyenletet. Ezzel ekvivalensek a következő állítások:

\begin{matrix} sin 3 ε & = cos 2 ε \\ sin 3 ε & = sin (\frac{π}{2} - 2 ε) \\ 3 ε & = \frac{π}{2} - 2 ε + 2 π k & vagy & 3 ε + \frac{π}{2} - 2 ε = π + 2 π l k, l \in Z \\ ε & = \frac{π}{10} + \frac{2 π}{5} k & vagy & ε = \frac{π}{2} + 2 π l . \end{matrix}

0 < ε < \frac{π}{4}

miatt az egyetlen megoldás

ε = \frac{π}{10} .

Beláttuk tehát:

I. Ha szerkeszthető az

1,2,2,

szögfelező szakaszokat tartalmazó háromszög, akkor szerkeszthető a

B B_{1} B_{2}

derékszögű háromszög, amelynek átfogója

B B_{1} = 2

, és amelyben

B_{1} B B_{2} ∢ = ε = 18^{\circ}

.
Kimutatjuk, hogy ennek megfordítása is igaz:

II. Ha szerkeszthető a

B B_{1} B_{2}

derékszögű háromszög, amelynek átfogója

B B_{1} = 2

, és

ε = 18^{\circ}

, akkor szerkeszthető az

1,2,2

szögfelező szakaszokat tartalmazó háromszög is.

2. ábra

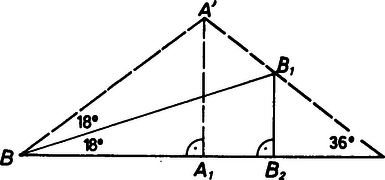
Tegyük fel, hogy szerkeszthető a mondott

B B_{1} B_{2}

derékszögű háromszög, akkor tükrözzük a

B B_{2}

félegyenest a

B B_{1}

-re, majd szerkesszünk a

B_{1}

-en átmenő, a

B B_{2}

-vel

36^{\circ}

-os szöget bezáró ‐

B A'

-vel nem párhuzamos ‐egyenest (l. a 2. ábra jelöléseit). Ily módon előáll az

A' B C'

egyenlő szárú háromszög, amelyben a szárakhoz tartozó szögfelezőszakaszok

2

egység hosszúak. Kérdés: a háromszög

m

magassága

1

egység-e? A szögfüggvények egyszerű alkalmazásával

\begin{matrix} B C' = B B_{2} + B_{2} C' = 2 cos 18^{\circ} + \frac{2 sin 18^{\circ}}{tg 36^{\circ}}, \\ B A_{1} = \frac{1}{2} B C', \end{matrix}

\begin{matrix} m = B A_{1} tg 36^{\circ} = tg 36^{\circ} cos 18^{\circ} + sin 18^{\circ} . \end{matrix}

(2)

18^{\circ}

és

36^{\circ}

szögfüggvényeinek pontos értékét egyszerűen meghatározhatjuk:

\begin{matrix} sin 18^{\circ} = \frac{\sqrt[]{5} - 1}{4}, cos 18^{\circ} = \frac{\sqrt[]{10 + 2 \sqrt[]{5}}}{4}, tg 36^{\circ} = \sqrt[]{5 - 2 \sqrt[]{5}}, \end{matrix}

ezeket (2)-be helyettesítve

m

-re tényleg

1

-et kapunk.

Ezzel beláttuk, hogy a II. állítás is igaz. Közismert, hogy a

18^{\circ}

-os szög megszekeszthető, tehát a II. előtagja igaz. Ebből következően a II. utótagja is igaz, azaz a feladat kérdésére igenlő a válasz.

b) Az a) alatti megoldás gondolatmenete az

A B C

egyenlő szárú háromszög alapszögét

2 φ

-vel jelölve a

sin 3 ε = cos 2 ε

helyett a

\begin{matrix} 3 sin 3 φ = 2 cos 2 φ \end{matrix}

egyenletre vezet. Ennek egyszerű megoldására alig számíthatunk. Alkalmazzuk

sin 3 φ

-re az addíciós tételeket, majd olyan lépések kínálkoznak, amelyek során a

φ

-nek csak a szinusza marad meg:

\begin{matrix} cos 2 φ (3 sin φ - 2) + 3 cos φ sin 2 φ = 0, \\ 12 sin^{3} φ - 4 sin^{2} φ - 9 sin φ + 2 = 0. & (3) \end{matrix}

Eddigi eredményünk: ha szerkeszthető az

1,3,3

szögfelező szakaszokat tartalmazó háromszög, akkor az egyenlő szárú, továbbá alapszöge felének szinusza szerkeszthető, és gyöke a

\begin{matrix} 12 x^{3} - 4 x^{2} - 9 x + 2 = 0 \end{matrix}

(4)

egész együtthatós harmadfokú egyenletnek.

Keressük meg a (4) racionális gyökeit!

Tegyük fel, hogy

p / q