| Cím: | Sorminták és egybevágósági transzformációk | ||
| Szerző(k): | Pálffy Péter Pál | ||
| Füzet: | 1993/április, 145 - 151. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A sík egybevágóságaival fogunk foglalkozni. Ezek közé tartoznak az eltolások, a forgatások, a tengelyes tükrözések. A sík egy egybevágósági transzformációján egy olyan leképezést (függvényt) értünk, amelynek értelmezési tartománya a sík pontjainak halmaza, és értékkészlete is ugyanezen sík pontjainak halmaza, továbbá tetszőleges pontpárra és távolsága megegyezik és távolságával. Hangsúlyozom, hogy egy egybevágósági transzformáció meghatározásához csak arra van szükség, hogy minden pontnak megadjuk a képét; azt az utat, ahogyan -ből -be jutunk, csak a leképezés szemléltetéséhez használjuk. Az ismert egybevágósági transzformációkat a következőképpen fogjuk jelölni: a vektorral való eltolást -vel, az pont körüli szögű irányított forgatást, -val, az egyenesre való tükrözést -vel. 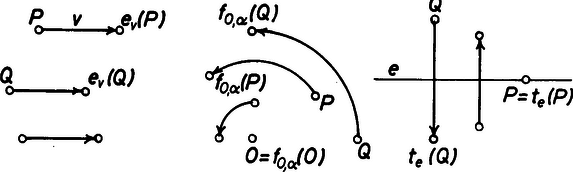 1. ábra Az egybevágóságok közé számítjuk a helybenhagyást (identikus függvényt), amelyre , minden pontra. Meg kell említenünk az egybevágósági transzformációknak még egy, kevésbé ismert fajtáját. Ez az úgynevezett csúsztatva tükrözés. Legyen egy egyenes, pedig egy -ben fekvő vektor. Ekkor a -vel jelölt transzformáció egy ponthoz az -re vonatkozó tükörképének -vel való eltoltját rendeli hozzá (2. ábra). 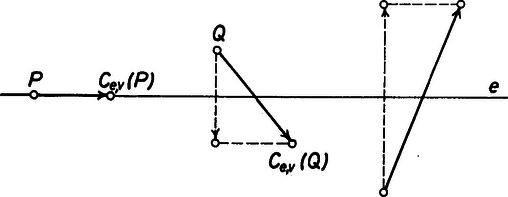 2. ábra Ahogyan a tengelyes tükrözést szokás úgy szemléltetni, hogy az tulajdonképpen az tengely körüli -os térbeli forgatás, a csúsztatva tükrözést is elképzelhetjük úgy, hogy az egy csavarmenetes tengely körüli térbeli forgatást jelent: miközben végrehajtjuk a -os forgatást, a tengely -vel előrehalad. Minden egybevágósági transzformációnak van inverze, azaz olyan egybevágósági transzformáció, ami -hez -t rendeli hozzá. Ezt a transzformációt -gyel jelöljük. Világos, hogy inverze a vektorral való eltolás, tehát továbbá , és . 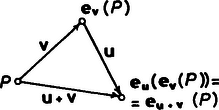 3. ábra Két egybevágósági transzformációt egymás után végrehajtva ismét egybevágósági transzformációt kapunk, hiszen mindkét leképezés megtartja a pontok távolságát. Az így keletkező egybevágósági transzformációt a két eredeti leképezés szorzatának nevezzük. Tehát a és egybevágósági transzformációk szorzata az a -gyel jelölt leképezés, amelyre . Nyilvánvalóan (3. ábra), , (illetve , ha ). Mielőtt továbbmennénk, vegyük észre, hogy három, nem egy egyenesen fekvő pont képe egyértelműen meghatározza az egybevágósági transzformációt, ugyanis távolsága -tól , -től , tehát az középpontú sugarú és az középpontú sugarú kör valamelyik metszéspontja (ill. érintési pontja, ha az egyenesen fekszik). A két metszéspont szimmetrikus az egyenesre, így távolságuk az ponttól különböző, ezért az feltétel egyértelműen kijelöli -t (4. ábra). 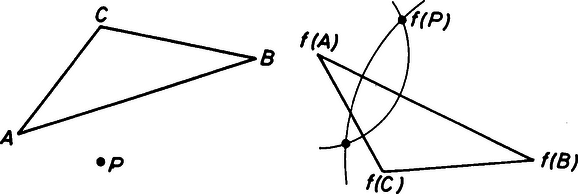 4. ábra Most már könnyen meghatározhatjuk két tükrözés szorzatát is. Ha tengelyeik azonosak, azaz , akkor . Ha és párhuzamosak, akkor , ahol jelöli azt az -re merőleges vektort, amely -et -be viszi. Ha és metsző egyenesek, akkor , ahol jelöli és metszéspontját, pedig az általuk bezárt szöget (-tól felé). Figyelembe véve, hogy három pont képe egyértelmuen meghatározza az egybevágósági transzformációt, ezek az összefüggések könnyen leolvashatók az 5. ábrából. 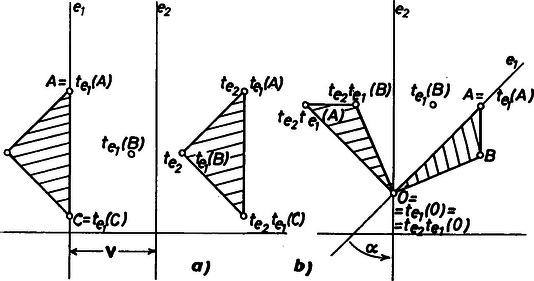 5. ábra A leképezések szorzására a következő összefüggések érvényesek: Az első összefüggést, a szorzás asszociativitását, a következőképpen láthatjuk be: . A (2) és (3) összefüggés az identikus leképezés, illetve az inverz definíciójából nyilvánvaló. Megjegyezzük, hogy a leképezések szorzása általában nem kommutatív, például párhuzamos tengelyű tükrözések szorzatára , de . 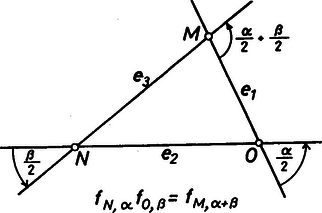 6. ábra Láttuk, hogy közös középpontú forgatások szorzata szintén forgatás, de vajon mi a helyzet, ha a két forgatás középpontja különböző? Vegyük tehát az és forgatásokat . Írjuk fel -t mint két -n átmenő egyenesre vonatkozó tükrözés szorzatát. Az egyik egyenes irányát tetszőlegesen választhatjuk, a másodiknak ezzel szöget kell bezárnia. Ugyanígy -t is felírhatjuk mint két -en átmenő, egymással szöget bezáró egyenesre vonatkozó tükrözés szorzatát. Az egyik egyenes szabadon választható, vegyük ezt mindkétszer az egyenesnek. Ekkor , tehát , ami az asszociativitást használva így alakítható: . Itt , így (2) szerint . Ha és párhuzamosak, akkor egy eltolást kapunk, ha metszők, akkor egy forgatást (6. ábra). Hasonlóan számíthatjuk ki egy forgatás és egy eltolás szorzatát is. Megmutatjuk, hogy minden egybevágósági transzformáció felírható két vagy három tükrözés szorzataként. Legyen egy tetszőleges egybevágósági transzformáció és vegyünk három, nem egy egyenesen fekvő pontot, jelölje ezeket és . Legyen szakasz felező merőlegese , illetve ha , akkor legyen tetszőleges, az -n átmenő egyenes. Ekkor , így , tehát szakasz felező merőlegese, , átmegy -n. (Ha , akkor vegyük -nek az egyenest.) Most és . Ha is teljesül, akkor , hiszen az és pontok képei egyértelműen meghatározzák az egybevágósági transzformációt. Ha , akkor ezek a pontok egymásnak az egyenesre vonatkozó tükörképei, így az előzőhöz hasonló érveléssel . (Az asszociatívitás miatt nem szükséges a szorzatot zárójeleznünk.) (7. ábra) 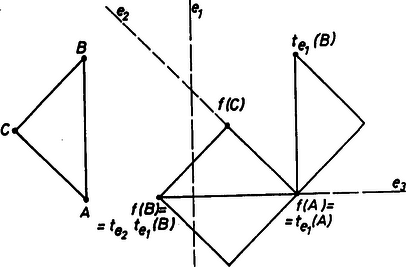 7. ábra Két tükrözés szorzata - mint már láttuk - vagy az identitás vagy egy eltolás vagy egy forgatás, aszerint, hogy a tengelyeik megegyeznek, párhuzamosak vagy metszők. Nézzük meg, hogy milyen transzformációkat kaphatunk három tükrözés szorzataként. Ha az első kettő szorzata az , akkor a szorzat egy tükrözés. Ha az első kettő szorzata az eltolás, akkor két esetet kell megkülönböztetnünk. Amennyiben merőleges az tengelyre is, akkor , ahol az tengelyt az egyenest -vel eltolva nyerjük. Ha viszont nem merőleges az tengelyre, akkor és metszi egymást egy pontban. Forgassuk el az körül az és egyeneseket úgy, hogy közbezárt szögük ne változzon, és elforgatottja, , merőleges legyen -re. Jelölje és metszéspontját . Most körül forgassuk el -et és -t úgy, hogy közbezárt szögük ne változzon, és , elforgatottja , párhuzamos legyen -vel. Ekkor , valamint , továbbá, mivel és párhuzamosak egymással és merőlegesek -re, következik, hogy , ahol párhuzamos -vel. Összefoglalva azt kapjuk, hogy , egy csúsztatva tükrözés. Hasonlóan beláthatjuk, hogy abban az esetben is, ha forgatás, akkor is vagy tükrözés, vagy csúsztatva tükrözés. Ezáltal igazoltuk, hogy nincs más egybevágósági transzformáció, csak a forgatások, az eltolások, a tükrözések, a csúsztatva tükrözések és az identitás. Vizsgáljuk meg, hogy mely pontok, illetve egyenesek képződnek önmagukra az egyes transzformációk során: négyzet : 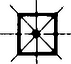 téglalap: 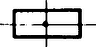 rombusz: 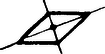 szimmetrikus trapéz: 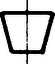 deltoid: 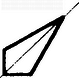 parallelogramma:  általános négyszög:  Hasonlóan, a lehetséges szimmetriák szerint fogjuk osztályozni a sormintákat is. Sormintának egy olyan alakzatot nevezünk, amely két párhuzamos egyenes közötti sávban helyezkedik el, és van olyan eltolás, amely az alakzatot önmagába viszi. (Ekkor természetesen az alakzat a ,,végtelenbe nyúlik'', de ábráinkon csak egy véges részletét tudjuk megrajzolni.) Feltételezzük, hogy van egy olyan legrövidebb vektor, , amivel való eltolás a sormintát önmagába viszi. Vegyünk most egy tetszőleges eltolást, amelyik a sormintát önmagára képezi le. Ha és iránya megegyezik, akkor legyen , ahol a vektor hosszát, az valós szám egész részét jelöli. Ekkor , és is szimmetriája a sormintának. Mivel a legrövidebb vektor volt, amivel a sorminta eltolható, ezért , azaz . Hasonlóan járhatunk el, ha és ellentétes irányúak, és azt nyerjük, hogy pontosan az eltolások azok, amelyek sormintánkat önmagába viszik. (Itt a nullvektorral való eltoláson az identikus leképezést értjük.) Mivel a sorminta minden szimmetriája a sáv középegyenesét önmagába kell vigye, az egybevágósági transzformációk fixegyeneseinek számbavételéből tudjuk, hogy csak a következő fajta szimmetriák jöhetnek szóba: 1. -vel párhuzamos eltolások 2. -n fekvó pontok körüli -os forgatások 3. -re merőleges egyenesekre vonatkozó tükrözések 4. -re való tükrözés, ill. tengelyű csúsztatva tükrözések. Jelöljük az egyes típusú szimmetriák halmazát rendre a következőképpen: . Már megmutattuk, hogy pontosan az alakú eltolásokból áll. Legyen most az osztályok valamelyike. Ha és -beli szimmetriák, akkor is szimmetriája a sormintának és ez minden esetben eltolás: , ahol , ahol az -re merőleges, -et -be vivó vektor (ez -n fekszik, mivel és merőleges -re, lásd 3. eset); . Tehát , így , valamely -re. Innen , azaz a osztály minden eleme felírható alakban, ahol egy rögzített eleme -nek. Az is könnyen ellenőrízhető, hogy minden alakú szimmetria ugyanabba az osztályba tartozik, mint , tehát a osztály elemei éppen az alakú egybevágósági transzformációk. Elófordulhat persze, hogy valamelyik osztály üres, az adott sormintának nincs ilyen típusú szimmetriája. Ha , akkor az alakú transzformációk mind -os forgatások és középpontjaik az tengelyen távolságra követik egymást. Ha , akkor az tükrözések tengelyei -re merőlegesek és egymástól távolságra helyezkednek el. Ha a csúsztatva tükrözés -hez tartozik, akkor a osztály az alakú csúsztatva tükrözésekből áll. Vegyük észre, hogy miatt ezekre a csúsztatva tükrözésekre két lehetőség adódik. Mivel a vektor -nak egész számszorosa kell legyen, ha , akkor a alakú csúsztatva tükrözésekből áll, beleértve tükrözést; ha viszont , akkor éppen a alakú csúsztatva tükrözések halmaza. Az első halmazt -lal, a másodikat -lel fogjuk jelölni. Végül vegyük észre, hogy esetén ! Például , ahol az és metszéspontjából -ba mutató vektort jelöli. Ennek alapján egy sorminta lehetséges szimmetriáira a következő esetek fordulhatnak elő: I) csak eltolások , II) eltolások és -os forgatások , III) eltolások és tükrözések , IV) eltolások és csúsztatva tükrözések, köztük az -re vonatkozó tükrözés is , V) eltolások és csúsztatva tükrözések, de az -re való tükrözés nem . A további esetekben a forgatások, tükrözések és csúsztatva tükrözések közül legalább kétféle fellép, de akkor az előző észrevétel szerint a harmadik fajta is, így a további lehetőségek: VI) és VII) . A hét lehetőség mindegyike valóban elő is fordul, amint azt az alábbi példák mutatják: I.  II. 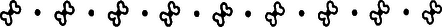 III.  IV. 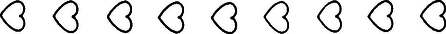 V.  VI. 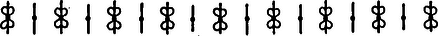 VII.  Megemlítem, hogy a sík ,,tapétázásai'' is hasonlóképpen osztályozhatók, itt olyan mintákat kell vizsgálni, amelyek két különböző irányú vektorral való eltolással is önmagukba vihetők. Az ilyen minták a szimmetriák szempontjából már 17-féle csoportba sorolhatók. A mór művészet díszítőmintái között mind a tizenhétfélére találunk példákat. A térbeli, három irányban ismétlődő minták a kristálytanban jutnak szerephez, itt már 230 lehetőség adódik. |