Kezdőlap


Cím:	1992. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):	Surányi János
Füzet:	1993/február, 51 - 55. oldal	PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Nevezzük $n$ adott pozitív szám különös közepének a számok négyzetösszegének és összegének hányadosát, harmadik hatványközepüknek pedig köbeik számtani közepének a köbgyökét. Döntsük el $n = 2$ esetén, hogy melyik igaz az alábbi állítások közül.
$a)$ A különös közép sohasem kisebb a harmadik hatványközépnél.
$b)$ A különös közép sohasem nagyobb a harmadik hatványközépnél.
$c)$ A különös közép a számok választásától függően lehet nagyobb és kisebb is a harmadik hatványközépnél.
Melyik állítás igaz $n = 3$ esetén?

I. megoldás. Legyenek az adott pozitív számok

a_{1}, a_{2} ..., a_{n}

. Tudjuk, hogy két pozitív szám közül a köbe a nagyobbnak lesz nagyobb, és hasonló áll a pozitív számszorosukra is. A két közép különbsége tehát ugyanolyan előjelű, mint a köbeik különbségének

n {(a_{1} + a_{2} + ... + a_{n})}^{3}

-szorosa.
Erre a kifejezésre

n = 2

esetén egyszerű átalakításokkal a következő azonosságot nyerjük:

\begin{matrix} 2 {(a_{1}^{2} + a_{2}^{2})}^{3} - {(a_{1} + a_{2})}^{3} (a_{1}^{3} + a_{2}^{3}) = {(a_{1} + a_{2})}^{3} (a_{1}^{3} - a_{2}^{3}) . \end{matrix}

Ha tehát

a_{1} = a_{2}

, akkor a különbség

0

, a két közép egyenlő, különben a jobb oldal két tényezője egyező előjelű, így szorzatuk pozitív; a különös közép tehát nagyobb a harmadik hatványközépnél. Eszerint két szám esetén az a) állítás igaz.
Három szám esetén viszont a

c)

állítás az igaz. Ennek igazolására elég megadni egyrészt három olyan számot, amelyek különös közepe nagyobb harmadik hatványközepüknél, másrészt három olyant, amelyekre a különös közép a kisebb. Az előbbi tulajdonságú az

1

1

2

hármas. Erre

\begin{matrix} 3 {(1^{2} + 1^{2} + 2^{2})}^{3} = 648, {(1 + 1 + 2)}^{3} (1^{3} + 1^{3} + 2^{3}) = 640. \end{matrix}

Az utóbbira példa a

2

2

3

hármas. Erre

\begin{matrix} 3 {(2^{2} + 2^{2} + 3^{2})}^{3} = 14739, {(2 + 2 + 3)}^{3} (2^{3} + 2^{3} + 3^{3}) = 14749. \end{matrix}

Ezzel igazoltuk az állítást.
Megjegyzés. Volt, aki három olyan számtól remélte, hogy a harmadik hatványközepük lesz a nagyobb, amelyek közt kicsi, egyenlő különbség van. Ez azonban nem következik be. Ha a három szám

a - b

a

a + b

, ahol

0 < b < a

, akkor a különös közép

\begin{matrix} \frac{{(a - b)}^{2} + a^{2} + {(a + b)}^{2}}{3 a} = a + \frac{2 b^{2}}{3 a}, \end{matrix}

a harmadik hatványközép köbe pedig

\begin{matrix} \frac{{(a - b)}^{3} + a^{3} + {(a + b)}^{3}}{3} = a^{3} + 2 a b^{2} . \end{matrix}

Mivel az előbbi érték köbe ezzel a két taggal kezdődik, és ehhez további két pozitív tag járul, így az ilyen számhármasoknak mindig a különös közepe nagyobb.

II. megoldás. Jegyezzük meg először, hogy ha a közepek nagyságviszonyát vizsgáljuk, akkor megszorozhatjuk mindegyik számot ugyanazzal a pozitív számmal, hiszen ekkor a két közép is ezzel a számmal szorzódik meg, nagyságviszonyuk tehát nem változik. Így feltehetjük, hogy a számok számtani közepe

1

, mert ha nem így volna, akkor eloszthatjuk mindegyiket a számtani középpel.
Vizsgáljuk a két közép viszonyát olyan számokra, amelyek közül

n - 1

egyenlő és kisebb mint

1

, tehát

1 - c

, ahol

0 < c < 1

, az

n

-edik pedig

1 + (n - 1) c

. Az első megoldás megjegyzésének megfelelően elég a közepek köbének a különbségét vizsgálni. Ez

\begin{matrix} {(\frac{n + n (n - 1) c^{2}}{n})}^{3} - \frac{n + 3 ((n - 1) + {(n - 1)}^{2}) c^{2} + (- (n - 1) + {(n - 1)}^{3}) c^{3}}{n} = \end{matrix}

\begin{matrix} = 1 + 3 (n - 1) c^{2} + 3 {(n - 1)}^{2} c^{4} + {(n - 1)}^{3} c^{6} - 1 - 3 (n - 1) c^{2} - (n - 1) (n - 2) c^{3} = \end{matrix}

\begin{matrix} = - (n - 1) c^{3} (n - 2 - 3 (n - 1) c - {(n - 1)}^{2} c^{3}) . \end{matrix}

Két szám

(n = 2)

esetén ez mindig pozitív, és jegyezzük meg, hogy ekkor az általános esettel van dolgunk, miután nincsenek egyenlő számok. Ekkor tehát az a) állítás az igaz.
Pozitív a kifejezés

2

-nél nagyobb

n

-re is, ha

c

elég nagy (de

1

-nél kisebb), pl.

c = \frac{2}{3}

. Ha viszont

c

kicsi, pl.

c = \frac{1}{4 (n - 1)}

, (és

n ⩾ 3

), akkor a zárójelben levő kifejezés

\begin{matrix} n - \frac{11}{4} - \frac{1}{64 (n - 1)} \geq n - \frac{353}{128} \geq \frac{384 - 353}{128} > 0. \end{matrix}

Ekkor tehát a harmadik hatványközép a nagyobb.
Azt nyertük tehát, a feladatban feltettnél általánosabb kérdésre adva választ, hogy

2

-nél több szám esetén mindig a

c)

állítás az igaz.
Megjegyzések. 1. A harmadik hatványközép lehet csupa különböző szám esetén is nagyobb a különös középnél. Három szám esetén pl. ‐ kényelem kedvéért egész számokra szorítkozva ‐ legyen két szám a

23

és a

25

. Azt vehetjük észre, hogy a harmadik számot

29

és

36

közt választva a harmadik hatványközép lesz a nagyobb, viszont

28

-at vagy

37

-et választva már a különös közép a nagyobb.
2. Meglepő eredményt kapunk, ha azt vizsgáljuk, hogy három szám esetén a harmadik hatványközép és a különös közép hányadosa mekkora lehet. Ez a hányados a maximumát az

1

1

\sqrt[]{2}

hármasra (és az ezzel arányosakra) veszi fel; a maximum értéke mindössze

\begin{matrix} \sqrt[3]{\frac{24 + 17 \sqrt[]{2}}{48}} = \sqrt[3]{\frac{1}{2} (1 + \sqrt[]{\frac{578}{576}}}) = 1, 00028902. \end{matrix}

2. Tetszőleges pozitív egész

k

-ra legyen

f_{1} (k)

a tízes számrendszerben felírt

k

szám jegyei összegének a négyzete és

n > 1

esetén legyen

f_{n} (k) = f_{1} (f_{n - 1} (k))

. Mennyi

f_{1992} (2^{1991})

?
Megoldás. A kérdésre annak alapján tudunk választ adni, hogy egyrészt a számjegyek számát határozzuk meg, másrészt a kérdezett szám maradékát, ha

9

-cel osztjuk.
Jelöljük a

2^{1991}

számot

K

-val.

\begin{matrix} K = 8^{\frac{1991}{3}} < 10^{664} . \end{matrix}

K

szám tehát legfeljebb

664

jegyű, s így jegyeinek az összege nem több mint

664 \cdot 9

, ami

6000

-nél kisebb. Eszerint

f_{1} (K) < 36 \cdot 10^{6}

. Eddig a korlátig a

29 999 999

szám jegyeinek az összege a legnagyobb,

65

. Így

\begin{matrix} f_{2} (K) \leq 4225. \end{matrix}

Hasonlóan számolva

\begin{matrix} f_{3} (K) \leq {(3 + 3 \cdot 9)}^{2} = 900. \end{matrix}

Egy legfeljebb háromjegyű

k

számra

f_{1} (k) \leq {(3 \cdot 9)}^{2} = 729

, tehát szintén legfeljebb háromjegyű. Így, ha

n \geq 3

, akkor

f_{n} (K)

legfeljebb háromjegyű.
Ismeretes, hogy egy szám

9

-cel osztva ugyanannyi maradékot ad, mint a számjegyeinek az összege; továbbá két szám szorzatának a maradéka, ha 9-cel osztunk, ugyanannyi, mint a maradékaik szorzatáé, mivel

(9 r + s) (9 t + u) = 9 (9 r t + r u + s t) + s u

. Ezek alapján

\begin{matrix} K = 2^{6 \cdot 331 + 5} = 64^{331} \cdot 32 = {(9 \cdot 7 + 1)}^{331} (9 \cdot 3 + 5) \end{matrix}

maradéka

5

, s így ennyi a számjegyei összegének a maradéka is.

f_{1} (K)

maradéka tehát annyi, mint

25

-é, azaz

7

;

f_{2} (K)

maradéka annyi, mint

49

-é, vagyis

4

;

f_{3} (K)

maradéka annyi, mint

16

-é, ami

7

. Ennyi a maradéka a számjegyei összegének is, és a szám legfeljebb háromjegyű, így a számjegyek összege csak

7

16

és

25

lehet.

f_{4} (K)

lehetséges értékei

49

256

és

625

f_{5} (K)

értéke már mind a három esetben ugyanaz:

169

. Folytatva a számolást

\begin{matrix} f_{6} (K) = 256, f_{7} (K) = 169, f_{8} (K) = 256. \end{matrix}

Világos, hogy innen periodikusan páros indexre

256

-ot kapunk, páratlanra

169

-et. A feladat kérdésére tehát a válasz

\begin{matrix} f_{1992} (2^{1991}) = 256. \end{matrix}

Megjegyzések. 1. Természetesen más

a

-ra,

e

-re és

n

-re is meghatározható hasonlóan

f_{n} (a^{c})

, és könnyen látható, hogy elég nagy

n

-re

169

-en és

256

-on kívül csak az

1

és a

81

fordul elő.
2. Számítógéppel meghatározható

2^{1991}

számjegyeinek az összege, ez

2669

. Innen

f_{1} (K) = 7123561

f_{2} (K) = 625

f_{3} (K) = 169

f_{4} (K) = 256

, és már innen ismétlődik periodikusan az utolsó két érték.

3. Adott a síkban véges sok pont, amelyek közül semelyik három nem esik egy egyenesre. Bizonyítsuk be, hogy kiszínezhetők két színnel úgy, hogy ne legyen olyan félsík, amely a pontok közül pontosan hármat tartalmaz, és azok egyszínűek.

Megoldás. Vegyük a ponthalmaz konvex burkát, azt a legkisebb sokszöget, amelyik az összes pontot tartalmazza. (Lásd az alábbi 1. megjegyzést). Ennek csúcsai az adott pontok közül valók, és a feltétel szerint az oldalszakaszok belsejére nem esik adott pont.
Egy olyan félsík, amelyikbe három adott pont esik, tartalmazza a pontok meghatározta háromszöget, így tartalmaz a konvex burok belsejében levő pontot. A határegyenese tehát átmetszi a konvex burkot, ezért a félsík tartalmazza a konvex burok legalább egy csúcsát.
A burok belsejében lehetnek az adott pontok közül olyanok, amelyeket egy olyan félsík sem tartalmaz, amelyikbe csak három adott pont esik. Ezek színezése a feladat követelményének teljesülését nem befolyásolja. Ez adhatja azt a gondolatot, hogy az összes belső pontot fessük ugyanolyanra, mondjuk kékre.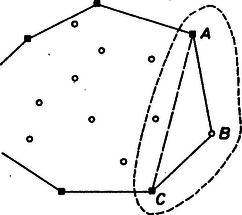

1. ábra

A burok csúcsait ezután több lépésben színezzük ki. Első lépésben fessük az összeset pirosra. Ha most van három szomszédos csúcs,

A

B

C

, amelyek meghatározta háromszög nem tartalmaz további adott pontot, akkor

B

színét változtassuk kékre (1. ábra). Ha ezután is maradt ilyen csúcs-hármas, akkor ismételjük az eljárást. Ez véges számú lépésben befejeződik.
Megmutatjuk, hogy így megfelelő színezéshez jutunk. Jegyezzük meg, hogy nem keletkezik a konvex burkon két szomszédos kék csúcs, mert ha egy csúcsot kékre festünk, akkor a szomszédos csúcsok már nem lehetnek olyan háromszög középső csúcsai, amelyiknek mind a három csúcsa piros.
Ha egy félsík három csúcsot tartalmaz, akkor az azok meghatározta háromszög nem tartalmaz további adott pontot, tehát vagy a középső csúcs kék, a két szomszédja piros, vagy azért nem változtattuk meg a középső csúcs színét, mert a csúcsok nem voltak egyszínűek.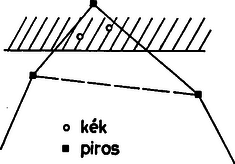

2. ábra

Ha két csúcsot tartalmaz a félsík, akkor tartalmaz a konvex burok belsejében lévő, tehát kék pontot, viszont a két csúcsnak legfeljebb az egyike lehet kék.
Ha végül a három pontot tartalmazó félsík egy csúcsot tartalmaz, akkor a határegyenese átmetszi az abból induló két oldalt (2. ábra). A tartalmazott csúcs és a két szomszédja tehát olyan háromszöget határoz meg, amelyik tartalmaz a burok belsejében levő (tehát kék) pontot, s így a csúcsot meghagytuk pirosnak. Ezzel állításunkat beláttuk.
Megjegyzések. 1. A sík egy véges ponthalmazának a konvex burkát megkaphatjuk például úgy, hogy választunk egy félsíkot, amelyik tartalmazza a ponthalmazt. Annak a határegyeneshez legközelebbi (egyik) pontján át a határegyenessel párhuzamost húzunk, majd ezt forgatjuk a rajta levő, vagy ha több van, az egyik szélső adott pont körül úgy, hogy a ponthalmaz az egyik oldalán legyen, amíg újabb adott pont nem kerül rá. Ezután ekörül, illetőleg megint a szélső körül forgatjuk tovább az egyenest ugyanabban az irányban (3. ábra). Az eljárás véges számú lépésben befejeződik azzal, hogy visszajutunk az egyenes kezdő helyzetéhez. A forgásközéppontok a keresett konvex burok csúcsai.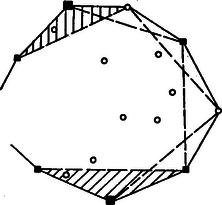

3. ábra

4. ábra

2. A megoldásban leírt eljárást adta meg Boda Péter. Ez láthatóan általában nem egyértelmű, több megfelelő színezéshez is vezethet aszerint, hogy hogyan választjuk azokat a háromszögeket, amelyek középső csúcsát átszínezzük.
A feladat többi megoldói a következő eljárást adták. A belső pontok kékre festése után pirosra festjük a konvex burok egy csúcsát, ha az a szomszédos csúcsokkal olyan háromszöget alkot, amelyik tartalmaz a belsejében adott pontot. Végül az esetleg színezetlenül maradt csúcsok alkotta íveken egy irányba haladva a szomszédos piros csúcs utánit kékre festjük, és a következőket felváltva pirosra és kékre, míg a következő piros csúcsig nem érünk (4. ábra), a burok két szélső csúcsa lehet kék is, piros is.
A leírt színezés is kiadja ezt, ha egy irányba haladva mindig a legközelebbi háromszöget vesszük, amelyiknek a középső csúcsát át kell színezni. Ebből látható, hogy ez az eljárás is megfelelő.