Kezdőlap


Cím:	Az 1992. évi (23.) Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Gnädig Péter , Szép Jenő
Füzet:	1992/november, 411 - 427. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elméleti feladatok

1. feladat: Forgó műhold
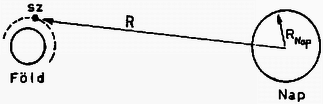
Egy műhold közelítőleg kör alakú pályán kering a Föld egyenlítői síkjában. A műhold egy elhanyagolható tömegű központi testből (

P

pont), és négy kicsi,

m

tömegű külső testből áll (

B

pontok). Ez utóbbiakat

r

hosszúságú, vékony nyújthatatlan kábelek kötik a

P

ponthoz. Mind az öt test (

P

és

B

pontokban) az Egyenlítő síkjában helyezkedik el, és forogva kering ebben a síkban. A négy sugárirányú kábelt egymással is vékony drótok kötik össze, amelyek a szomszédos kábeleket állandóan

90^{\circ}

-os szögben tartják (lásd az 1. ábrát).

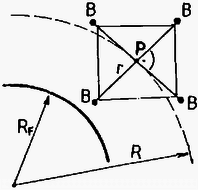1. ábra

Az összekötő drótok csak azért vannak, hogy megakadályozzák az egyes

B

-beli testek lengését. (Enélkül a mozgás vizsgálata hihetetlenül bonyolulttá válna.) Így valamennyi

B

-beli test ugyanazzal az

ω

szögsebességgel kering a

P

pont körül (az állócsillagokhoz viszonyítva); a rendszer merev testként forog.

-

Vizsgáld meg az alábbi kérdéseket általánosságban, minden lehetőséget diszkutálva. Az 1. és 2. alkérdésre numerikus választ is adjál! (A szükséges számadatokat a feladat végén találod.)

1. Határozd meg a sugárirányú kábelek által a

B

-beli testekre kifejtett erőt azokban a helyzetekben, amikor a

\vec{R}

és

\vec{r}

vektorok egyirányúak, ellentétes irányúak, illetve merőlegesek. Ezek a helyzetek felelnek meg a legnagyobb és a legkisebb kábelerőnek.

2. Mind a négy

B

-beli testben azonos, napenergiával működő gép található, amelyek a sugárirányú kábelekhez csatlakoznak. Mindegyik gép rövid idő alatt kissé behúzza a kábelt

B

-be, amikor az erő az előző kérdésnek megfelelően maximális, és kiengedi a kábelt ugyanannyival, ha az erő minimális. A kábelt a teljes hossz

1 %

-ával húzza be, illetve engedi ki a gép. Hosszú idő alatt a kábel átlagos hossza nem változik. Mekkora egy-egy gép egy körülfordulás alatti átlagos teljesítménye?

-

Az átlagos teljesítmény definíciója a következő: [(A gép által a kábel behúzásakor végzett munka)

-

(a drót által a kiengedéskor végzett munka)] osztva a körülfordulás idejével.

3. Elemezd, hogy milyen változást okoz lassan a műhold mozgásában a gép működése! Vizsgáld meg az alábbi táblázatban felsorolt mennyiségek megváltozásának lehetőségét. Az eredményeket a táblázat megfelelő rovataiba írd be!

TÖLTSD KI EZT A TÁBLÁZATOT A SZÁMÍTÁSAID ALAPJÁN,
EGYENLŐSÉGEK, EGYENLŐTLENSÉGEK, ESETLEG RÖVID SZÖVEG FORMÁJÁBAN

\begin{matrix} Az alábbi, & növekszik, & csökken, & nem & sohasem \\ aláhúzott̲ \end{matrix}

ha:ha:változikváltozik mennyiségha:A műhold keringési

sebessége̲A műhold pályájának

R sugara̲A műhold forgásának

ω

szög-̲

sebessége̲A műhold gravitációs

potenciális̲

energiája̲

Kerülhet-e a műhold a gépek által végzett munka hatására egy magasabb keringési pályára?
Kerülhet-e a műhold tetszőlegesen magas, a Föld gravitációs terét lényegében elhagyó pályára? Miért?

A numerikus számításokat a következő adatokkal végezd:
1. A középső test körpályájának

R

sugara:

R_{F} + 500

km.
2. A sugárirányú kábelek átlagos hossza

r = 100

km, tehát a műholdrendszer átmérője

200

km.
3. Az egyes tömegek:

m = 1000

kg.
4. A kezdetben a négy

B

-beli test (az állócsillagokhoz képest) a

P

pont körül óránként

10

fordulatot tesz meg.
5. A drótok, a kábelek és a központi

P

test tömege elhanyagolható.

Tanácsok:

$-$	Vedd figyelembe, hogy $ω$ kétféle előjelű is lehet!

$-$	Nem várunk egzakt megoldást, $5 %$ pontosságú eredmények tökéletesen elfogadhatóak.

$-$	A Hold és a Nap gravitációs hatását ne vedd figyelembe!

Felhasználható adatok:

\begin{matrix} Föld tömege: & M_{F} & = 5, 97 \cdot 10^{24} kg,a gravitációs állandó:G=6,673\cdot10^{- 11} m^{3}{kg}^{- 1}s^{- 2},a Föld egyenlítői sugara:R_{F}=6378 km.Jelöld a M_{F} G szorzatot K -val:K=3,983\cdot10^{14} m^{3} s^{- 2}. \end{matrix}

Megoldás. 1. A műhold

P

tömegközéppontja jó közelítéssel időben állandó

R

sugarú körpályán kering, szögsebessége

Ω

. (Pontosabb számítások szerint a tömeg-középpont helyzete a műhold forgása során egy kicsit ,,fel-le'' imbolyog, hullámvasútszerű mozgást végez.) A rendszer egészének mozgásegyenletéből

\begin{matrix} G \frac{M_{F} \cdot 4 m}{R^{2}} = 4 m \cdot R Ω^{2}, \end{matrix}

azaz

\begin{matrix} G M_{F} (= K) = R^{3} Ω^{2} . \end{matrix}

(1)

B

-beli testek gyorsulása két vektor összegeként állítható elő. Egyrészt maga a

P

pont

R Ω^{2}

nagyságú és a Föld középpontja felé irányuló gyorsulással mozog, az egyes

B

-beli testek pedig

P

-hez képest

r ω^{2}

nagyságú és

P

irányába mutató gyorsulással rendelkeznek (2.ábra).

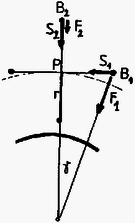2. ábra

A továbbiakban

r ≪ R

miatt az

1

nagyságrendű számok mellett elhanyagoljuk az

{(r / R)}^{2}

-tel arányos kifejezéseket és csupán az

r / R

rendű tagokat tartjuk meg. A

r / R

nagyságrendű szögek szinuszát magával a szöggel, koszinuszát pedig

1

-gyel közelítjük.
A

B_{1}

pontban a gravitációs erő nagysága (

\sqrt[]{R^{2} + r^{2}} \approx R

felhasználásával)

\begin{matrix} F_{1} = G \frac{M_{F} \cdot m}{R^{2}}, \end{matrix}

(2)

irányát pedig a

γ \approx r / R

szög jellemzi. A mozgásegyenlet ,,vízszintes'' komponense

\begin{matrix} F_{1} \cdot sin γ + S_{1} = m r ω^{2}, \end{matrix}

innen a fonalat feszítő erőre (1) és (2) felhasználásával

\begin{matrix} S_{1} = m r (ω^{2} - Ω^{2}) \end{matrix}

(3)

adódik.
A

B_{2}

pontban a gravitációs erő nagysága

\begin{matrix} F_{2} = G \frac{M_{F} \cdot m}{{(R + r)}^{2}}, \end{matrix}

a test ,,lefelé'' mutató gyorsulása pedig

R Ω^{2} + r ω^{2}

, a mozgásegyenlet tehát

\begin{matrix} F_{2} + S_{2} = m (R Ω^{2} + r ω^{2}), \end{matrix}

ahonnan a fonalat feszítő erő

\begin{matrix} S_{2} = m r ω^{2} + m R Ω^{2} (1 - \frac{r^{2}}{{(R + r)}^{2}}) \approx m r (ω^{2} + 2 Ω^{2}) . \end{matrix}

(4)

Általánosan belátható, hogy a ,,függőlegessel''

α

szöget bezáró kábeleket feszítő erő

\begin{matrix} S (α) = m r [ω^{2} + Ω^{2} (3 cos^{2} α - 1)], \end{matrix}

tehát

S

periódusonként valóban kétszer (

α = 0

és

180^{\circ}

-nál) veszi fel a legnagyobb

S_{max} = S_{2}

, kétszer (

α = 90^{\circ}

és

270^{\circ}

-nál) pedig a legkisebb

S_{min} = S_{1}

értéket. Az itt kiszámított erőket árapály-erőknek nevezik.

2. A legnagyobb és a legkisebb kábelerő különbsége

\begin{matrix} Δ S = S_{max} - S_{min} = 3 m r Ω^{2} . \end{matrix}

numerikusan

\begin{matrix} Ω = \sqrt[]{\frac{K}{R^{3}}} = 1, 1 \cdot 10^{- 3} s^{- 1}, ω = 2 π \frac{10}{3600 s} = 0, 17 s^{- 1}, Δ S = 367 N. \end{matrix}

Körülfordulásonként, vagyis

T_{0} = 360

másodpercenként

\begin{matrix} W = 2 \cdot Δ S \cdot Δ r = 2 \cdot 367 N \cdot 10^{3} m=7,34\cdot10^{5} J \end{matrix}

munkát végez a gép, az átlagos teljesítménye tehát

\begin{matrix} P = \frac{W}{T_{0}} = 2, 0 kW. \end{matrix}

(A ,,körülfordulást'' itt most a Földhöz képest kell érteni, nem pedig az állócsillagokhoz képest; mivel azonban

ω ≫ Ω

, a kétféle idő között alig van különbség!)

3. A rendszer teljes energiája

\begin{matrix} E = 4 m (- \frac{K}{R} + \frac{1}{2} r^{2} ω^{2} + \frac{1}{2} R^{2} Ω^{2}), \end{matrix}

s mivel ez

Δ t

idő alatt

P \cdot Δ t

értékkel növekszik, az

R, ω

és

Ω

mennyiségek fokozatosan megváltoz(hat)nak. Az (1) mozgásegyenlet szerint

\begin{matrix} Ω = \sqrt[]{\frac{K}{R^{3}}}, \end{matrix}

így

\begin{matrix} E (R, ω) = 2 m (r^{2} ω^{2} - \frac{K}{R}) . \end{matrix}

(5)

A rendszernek a Föld középpontjára vonatkoztatott perdülete időben állandó kell legyen, hiszen a belső erőkön kívül csak a Föld közepe felé irányuló erők hatnak.

\begin{matrix} J = 4 m (\pm r^{2} ω + R^{2} Ω) = állandó, \end{matrix}

illetve (1) felhasználásával

\begin{matrix} J (R, ω) = 4 m (\pm r^{2} ω + \sqrt[]{K \cdot R}) = állandó . \end{matrix}

(6)

A fenti képletben

ω > 0

és a

\pm

jel a műhold kétféle forgásirányára utal.
a) Ha a műhold forgása és a keringése ellentétes irányú, akkor (6) szerint (a negatív előjellel számolva)

R

és

ω

változása azonos előjelű. Mivel

R

és

ω

csökkenésével (5) szerint

E

is csökkenne, a valóságban pedig

Δ E > 0

, így ténylegesen

Δ R > 0

és

Δ ω > 0

kell teljesüljön; ugyanakkor viszont

Δ Ω < 0

. A ,,visszafele'' forgó műhold tehát a gépek működése következtében eltávolodik a Földtől, forgási szögsebessége nő, keringési szögsebessége és keringési sebessége ugyanakkor csökken.
b) Tárgyaljuk most azt az esetet, amikor a műhold ,,előrefelé'', a keringésével azonos irányban forog. A (6) egyenlet szerint (pozitív előjellel számolva)

\begin{matrix} ω = \frac{J}{4 m r^{2}} - \frac{\sqrt[]{K \cdot R}}{r^{2}}, \end{matrix}

ahonnan az

ω

és

R

mennyiségek kicsiny

Δ ω

és

Δ R

megváltozására fenn kell álljon

\begin{matrix} Δ ω = - \frac{1}{2 r^{2}} \sqrt[]{\frac{K}{R}} \cdot Δ R . \end{matrix}

A rendszer energiájának növekedése

\begin{matrix} Δ E = 2 m (2 r^{2} ω Δ ω + \frac{K}{R^{2}} Δ R) = 2 m \frac{K}{R^{2}} (1 - \frac{ω}{Ω}) \cdot Δ R . \end{matrix}

Mivel

Δ E > 0

és (3) szerint

ω > Ω

(hiszen ellenkező esetben a kábel meglazulna!), így

Δ R < 0

. A gép működésének hatására tehát a pályasugár csökken, a forgás szögsebessége és a keringés szögsebessége viszont nő.
A műhold pályasugarát pozitív munkavégzéssel növelni

-

mint láttuk,

-

csak akkor lehet, ha a műhold a keringési irányához képest visszafele forog. Adott

J

perdület esetén, mint az (6)-ból leolvasható, nagyon nagy

R

-nél

ω \sim \sqrt[]{R}

, a rendszer energiája pedig

E \sim R

. A műhold tehát az árapály-motort működtetve (véges nagyságú munkavégzés eredményeképpen) nem képes a Földtől nagyon messze kerülni, ,,elhagyni'' a Föld gravitációs terét! (A táblázat a fentiek alapján értelemszerűen kitölthető.)
Érdekes, hogy a műhold a

P

ponthoz csatlakoztatott kábelek ki-be huzigálásával képes a

P

pont körüli forgás szögsebességét csökkenteni, vagy éppen növelni. Nem helyes az az érvelés, hogy mivel a

P

-hez rögzített koordináta-rendszerből nézve centrális erők hatnak, a

P

-re vonatkoztatott perdület állandó marad. Azért hibás ez az érvelés, mert a

P

-hez rögzített koordinátarendszer nem inercia-rendszer, benne a perdület-tétel szokásos megfogalmazása nem érvényes! (Egy piruettező műkorcsolyázó is képes a saját forgási szögsebességét megnövelni olymódon, hogy a karjait behúzza.) A perdület-megmaradás tételét csak a forgásból és a keringésből adódó perdületek összegére tudjuk alkalmazni; külön az egyik, illetve a másik impulzusnyomaték-összetevő változhat a mozgás során!

2. feladat: Lineáris molekula longitudinális mozgása

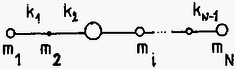1. ábra

N

atomos lineáris molekula

Ebben a feladatban egy lineáris molekula longitudinális, vagyis a molekula tengelyének irányába eső mozgását vizsgáljuk. A molekula forgásával, vagy elgörbülésével nem foglalkozunk. A molekula

N

atomból áll, ezek tömege rendre

m_{1}, m_{2}, ..., m_{N}

. Úgy vesszük, hogy mindegyik atom csak a legközelebbi szomszédjához kapcsolódik kémiai kötéssel. Mindegyik kötést tömegnélküli, a Hooke-törvénynek eleget tevő rugóval közelítjük. A kötéseknek megfelelő rugóállandók:

k_{1}, k_{2}, ..., k_{N - 1}

, az 1. ábrának megfelelően.
A megoldáshoz felhasználhatod a következőket:
Egy lineáris molekula longitudinális rezgőmozgása egymástól független rezgésekből, úgynevezett normálmódusokból (vagy normálrezgésekből) tevődik össze, szuperponálódik. Az egyes normálmódusokban mindegyik atom azonos frekvenciájú harmonikus rezgőmozgást végez, és ugyanakkor halad át az egyensúlyi helyzetén.
1. Legyen

x_{i}

i

-edik atom elmozdulása az egyensúlyi helyzetétől. Fejezd ki az

i

-edik atomra ható

F_{i}

eredő erőt (minden

i

-re) az

x_{1}, x_{2}, ..., x_{N}

elmozdulások és a kötések

k_{1}, k_{2}, ..., k_{N - 1}

rugóállandói függvényében! Milyen összefüggést fedezel fel az

F_{1}, F_{2} ..., F_{N}

erők között? Felhasználva ezt az összefüggést, találj kapcsolatot az

x_{1}, x_{2}, ..., x_{N}

elmozdulások között, és add meg ennek fizikai jelentését!

2. Vizsgáld meg a 2. ábrán látható kétatomos

A B

molekula mozgását!

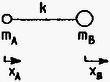2. ábra
Kétatomos AB
molekula

A kötés rugóállandója

k

. Add meg az

A

és

B

atomra ható erőket meghatározó kifejezéseket! Határozd meg a molekula lehetséges mozgásformáját! Számítsd ki a molekula rezgési frekvenciáját, és értelmezd az eredményt. Hogyan lehetséges az, hogy az atomok ugyanazzal a frekvenciával rezegnek, pedig a tömegük különböző?
3. Tanulmányozd egy háromatomos molekula,

A_{2} B

mozgását (3. ábra)!

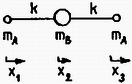3. ábra
Az

A_{2} B

háromatomos
molekula

Fejezd ki minden egyes atomra a visszatérítő erőt, mint csak a szóban forgó atom kitérésének függvényét! Vezesd le a molekula lehetséges mozgásait és a megfelelő rezgési frekvenciákat!

4. A

{C O}_{2}

molekula két longitudinális rezgési módusának frekvenciája

3, 998 \cdot 10^{13}

Hz, illetve

7, 042 \cdot 10^{13}

Hz. Próbáld meghatározni a C

-

O kötés rugóállandóját numerikusan! Mit gondolsz, mennyire pontosan közelíti a molekulakötés modellje a valódi molekulák rezgőmozgását?
A szén relatív atomtömege

12

, az oxigéné

16

, az atomtömeg egysége pedig

1, 660 \cdot 10^{- 27}

kg.

Megoldás. 1. Az egyes atomokra ható erők:

\begin{matrix} F_{1} & = k_{1} (x_{2} - x_{1}), \\ F_{2} & = k_{2} (x_{3} - x_{2}) - k_{1} (x_{2} - x_{1}), \\ ⋮ \\ F_{i} & = k_{i} (x_{i + 1} - x_{i}) - k_{i - 1} (x_{i} - x_{i - 1}), \\ ⋮ \\ F_{N} & = - k_{N - 1} (x_{N} - x_{N - 1}) . \end{matrix}

Látható, hogy

\begin{matrix} F_{1} + F_{2} + ... + F_{N} = 0. \end{matrix}

(1)

Ez az összefüggés azt fejezi ki, hogy a rendszer részeire csak belső erők hatnak, s ezeket összegezve Newton III. törvénye értelmében nullát kell kapjunk.
A rendszer mozgásegyenletei:

\begin{matrix} F_{i} = m_{i} a_{i} (i = 1, 2, ..., N), \end{matrix}

ahonnan (1) alapján

\begin{matrix} m_{1} a_{1} + m_{2} a_{2} + ... + m_{N} a_{N} = 0, \end{matrix}

továbbá

\begin{matrix} m_{1} v_{1} + m_{2} v_{2} + ... + m_{N} v_{N} = M V_{0} = állandó, \end{matrix}

valamint

\begin{matrix} m_{1} x_{1} + m_{2} x_{2} + ... + m_{N} x_{N} = M (V_{0} \cdot t + X_{0}) \end{matrix}

adódik, ahol

M

a rendszer össztömege,

V_{0}

a tömegközéppont sebessége,

X_{0}

pedig a tömegközéppont helyzete a kezdőpillanatban. Alkalmasan választott

-

a tömegközépponttal együttmozgó

-

koordináta-rendszerből nézve

V_{0} = 0

és

X_{0} = 0

, ebben a koordináta-rendszerben tehát

\begin{matrix} m_{1} x_{1} + m_{2} x_{2} + ... + m_{N} x_{N} = 0. \end{matrix}

(2)

2. Ebben az egyszerű esetben

\begin{matrix} F_{A} & = - k (x_{A} - x_{B}), \\ F_{B} & = - k (x_{B} - x_{A}) = - F_{A} . \end{matrix}

A tömegközépponti rendszerből nézve

m_{A} x_{A} + m_{B} x_{B} = 0

, ahonnan pl.

x_{B}

-t kifejezve és az

A

test mozgásegyenletébe helyettesítve

\begin{matrix} a_{A} = - \frac{k}{m_{A}} (1 + \frac{m_{A}}{m_{B}}) x_{A} \end{matrix}

adódik. Ez egy olyan harmonikus rezgőmozgás egyenlete, melynek körfrekvenciája

\begin{matrix} ω = \sqrt[]{k \frac{m_{A} + m_{B}}{m_{A} m_{B}}} . \end{matrix}

Mivel ez a kifejezés a két részecske tömegadatait szimmetrikusan tartalmazza, a másik részecske rezgési frekvenciája is ugyanekkora. A különböző tömegű testek azonos nagyságú erő hatására azért mozoghatnak ugyanakkora frekvenciával, mert a rezgési amplitúdójuk

-

és ezzel együtt a gyorsulásuk

-

a tömegükkel fordítottan arányos. (Megjegyezzük, hogy az

m_{A} m_{B} / (m_{A} + m_{B})

kifejezést a két részecskéből álló rendszer redukált tömegének nevezik.)
A két atom helyzete általánosan az

\begin{matrix} x_{A} (t) & = V_{0} \cdot t + X_{0} + C \cdot cos (ω t - α), \\ x_{B} (t) & = V_{0} \cdot t + X_{0} - C \cdot \frac{m_{A}}{m_{B}} cos (ω t - α) \end{matrix}

függvényekkel adható meg, ahol

V_{0}, X_{0}, C

és

α

a kezdeti feltételektől függő állandók.

3. A mozgásegyenletek most:

\begin{matrix} m_{A} a_{1} = k (x_{2} - x_{1}), & (3) \\ m_{B} a_{2} = k (x_{3} - 2 x_{2} + x_{1}), & (4) \\ m_{A} a_{3} = k (x_{2} - x_{3}) . & (5) \end{matrix}

,,Üljünk bele'' a tömegközépponti koordináta-rendszerbe, itt (2) értelmében

\begin{matrix} m_{A} (x_{1} + x_{3}) + m_{B} x_{2} = 0, \end{matrix}

tehát

\begin{matrix} x_{2} = - \frac{m_{A}}{m_{B}} (x_{1} + x_{3}) . \end{matrix}

Helyettesítsük be

x_{2}

fenti kifejezését mondjuk a (3) és (5) egyenletekbe:

\begin{matrix} m_{A} a_{1} = - k \frac{m_{A} + m_{B}}{m_{B}} x_{1} - k \frac{m_{A}}{m_{B}} x_{3}, & (6) \\ m_{A} a_{3} = - k \frac{m_{A}}{m_{B}} x_{1} - k \frac{m_{A} + m_{B}}{m_{B}} x_{3} . & (7) \end{matrix}

Keressük a fenti egyenletek megoldását (a feladat útmutatása alapján)

\begin{matrix} x_{1} = A_{1} \cdot cos (ω t); x_{3} = A_{3} \cdot cos (ω t) \end{matrix}

alakban, ahol

ω

a normálrezgés ‐ egyelőre ismeretlen ‐ körfrekvenciája. Nyilván fennáll, hogy

a_{1} = - ω^{2} x_{1}

és

a_{3} = - ω^{2} x_{3}

. A próbamegoldást (6) és (7)-be helyettesítve

\begin{matrix} m_{A} m_{B} ω^{2} A_{1} & = k (m_{A} + m_{B}) A_{1} + k m_{A} A_{3}, & (8) \\ m_{A} m_{B} ω^{2} A_{3} & = k m_{A} A_{1} + k (m_{A} + m_{B}) A_{3} . & (9) \end{matrix}

A fenti egyenletekből az

A_{1}

és

A_{3}

amplitudóknak csak az arányát lehet meghatározni, külön-külön a nagyságukat nem. Az

A_{1} / A_{3}

arányt kifejezve (8)-ból és (9)-be helyettesítve

ω^{2}

-re egy másodfokú egyenletet kapunk, melynek megoldásai:

\begin{matrix} ω_{1} = \sqrt[]{\frac{k}{m_{A}}}, ekkor \frac{A_{1}}{A_{3}} = - 1, \end{matrix}

(10)

illetve

\begin{matrix} ω_{2} = \sqrt[]{\frac{k (2 m_{A} + m_{B})}{m_{A} \cdot m_{B}}}, ilyenkor \frac{A_{1}}{A_{3}} = + 1. \end{matrix}

(11)

A (10)-nek megfelelő normálmódusban

x_{2} \equiv 0

, a középső atom mozdulatlan, a két szélső pedig egyforma amplitúdójú, de egymással ellentétes fázisú rezgést végez (4. ábra).

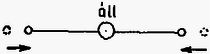4. ábra

A másik rezgési módusban a két szélső atom azonos fázisban egyforma amplitúdóval rezeg, míg a középső atom kitérése:

\begin{matrix} x_{2} = - 2 \frac{m_{A}}{m_{B}} x_{1}, \end{matrix}

tehát ez a másik kettővel ellentétes fázisú mozgást végez (5. ábra).

5

. ábra

4. A széndioxid molekula megadott rezgési frekvenciáit a fenti normálmódusok frekvenciáival azonosítva (a részecskék tömegének ismeretében) kiszámíthatjuk a

k

,,rugóállandót''. Az egyik módusból

k \approx 1420

N/m, a másikból

k \approx 1670

N/m adódik. Az eltérés nagyságrendje arra utal, hogy a molekularezgések itt tárgyalt modellje csak elég durván, első közelítésben írja le a jelenséget.

3. feladat: Egy űrszonda a napfényben
Ebben a feladatban egy űrszonda hőmérsékletét fogjuk kiszámítani. Az űrszonda teste egy

1

m átmérőjű gömbnek tekinthető, amelynek hőmérséklete mindenütt ugyanakkora. A szonda teljes felületét egyféle anyaggal burkolták. Az űrszonda a Föld közelében tartózkodik, de nincs a Föld árnyékában.
A Nap felületi hőmérséklete (feketetest sugárzási hőmérséklete)

T_{Nap} = 6000

K, a Nap sugara

6, 96 \cdot 10^{8}

m. A Nap

-

Föld távolság

1, 5 \cdot 10^{11}

m. A napsugárzás hatására az űrszonda olyan hőmérsékletre melegszik fel, hogy a napfényből elnyelt teljesítmény megegyezzék a szonda mint feketetest által kisugárzott teljesítménnyel. A feketetest egységnyi felülete által kisugárzott teljesítményt a

P = σ \cdot T^{4}

Stefan

-

Boltzmann-törvény adja meg, ahol

σ = 5, 67 \cdot 10^{- 8} Wm^{- 2}K^{- 4}

egy univerzális állandó. Első közelítésben feltételezhetjük, hogy mind a Nap, mind az űrszonda teljes mértékben elnyeli az őt érő elektromágneses sugárzást.

1. Vezess le összefüggést, amely megadja az űrszonda

T

hőmérsékletét! Számítsd ki számszerűen

T

értékét!

2. Egy

T

hőmérsékletű feketetest sugárzásának

u (T, f)

spektrumát a Planck-féle sugárzási törvény határozza meg:

\begin{matrix} u (T, f) d f = \frac{8 π k^{4} T^{4}}{c^{3} h^{3}} \cdot \frac{η^{3} \cdot d η}{e^{η} - 1}, \end{matrix}

ahol

u \cdot d f

[f, f + d f]

frekvencia-intervallumba eső elektromágneses sugárzás energiájának térfogati sűrűsége, továbbá

η = h f / k T

. Az állandók értékei: a Planck-állandó

h = 6, 6 \cdot 10^{- 34}

J/s; a Boltzmann-állandó

k = 1, 4 \cdot 10^{- 23}

J/K; a fénysebesség pedig

c = 3, 0 \cdot 12^{8}

m/s.
Ha a feketetest sugárzási spektrumát az összes

f

frekvenciára és a kisugárzás valamennyi irányára integráljuk, az egységnyi felület által kisugárzott teljes teljesítmény megfelelő

P = σ \cdot T^{4}

képletét kapjuk, összhangban a fent említett Stefan

-

Boltzmann-törvénnyel

(σ = 2 π^{5} k^{4} / (15 c^{2} h^{3}))

. Az 1. ábra a normált spektrumot, vagyis

\begin{matrix} \frac{c^{3} h^{3}}{8 π k^{4}} \cdot \frac{u (T, f)}{T^{4}} \end{matrix}

értékét mutatja

η

függvényében.

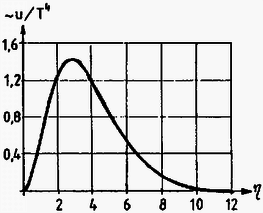1. ábra

Az űrszondákat általában hűteni kell, annyira, amennyire csak lehet. A szondák hűtésére a mérnökök olyan fényvisszaverő borítást alkalmaznak, amely egy bizonyos küszöbértéknél nagyobb frekvenciákra visszaveri a fényt, de az ennél alacsonyabb frekvenciájú hősugárzást nem akadályozza meg. Tegyük fel, hogy ennek az (éles) küszöbfrekvenciának megfelelő

h f / k

érték

1200

K.
Becsüljük meg, hogy ilyen körülmények között mekkora lesz az űrszonda hőmérséklete!

Megjegyzés. Nem kívánunk egzakt megoldást. Ne végezz bonyolult integrálásokat, ahol szükséges, alkalmazz közelítéseket! Felhasználhatod, hogy

\begin{matrix} \int_{0}^{\infty} \frac{η^{3} d η}{e^{η} - 1} = \frac{π^{4}}{15}, \end{matrix}

és az

η^{3} / (e^{η} - 1)

kifejezés

η \approx 2, 82

-nél maximális. Kis

η

esetén az exponenciális függvény

e^{η} \approx 1 + η

módon közelíthető.

3. A valódi űrszondáknál, amelyek kiterjesztett napelemei áramot termelnek, a szonda testének belsejében egy extra hőforrást jelent az elektronikus áramkörökben termelődő hő. Feltéve, hogy ennek a belső hőtermelésnek

1

kW a teljesítménye, mekkora volna a fenti 2. pontban vizsgált szonda hőmérséklete?

4. Egy festékgyár a következőképp hirdeti speciális festékét:
,,Ez a festék az összes bejövő (látható és infravörös) sugárzásnak

90 %

-át visszaveri, míg minden frekvencián (látható és infravörös tartományban) feketetestként sugároz, s ezzel sok hőt von el az űrszondától. Ily módon a festékünkkel annyira lehűtheti az űrszondáját, amennyire csak lehetséges.''
Létezhet-e ilyen festék? Miért, vagy miért nem?

5. Milyen tulajdonságú borításra van szükség ahhoz, hogy az előbbi szondához hasonló gömb alakú test hőmérsékletét az 1. alkérdésben számított érték fölé emeljük?

Megoldás. 1. A Naptól

R

távolságban az egységnyi felületre jutó sugárzási teljesítmény

\begin{matrix} P_{1} = \frac{4 π R_{Nap}^{2} \cdot σ T_{Nap}^{4}}{4 π R^{2}}, \end{matrix}

ebből az űrszonda

\begin{matrix} P_{elnyelt} = P_{1} \cdot {r^{2}}_{szonda} π \end{matrix}

mennyiséget nyel el. Másrészt a szonda teljes felülete által kisugárzott teljesítmény

\begin{matrix} P_{kisugárzott} = 4 r_{szonda}^{2} π \cdot σ T_{szonda}^{4} . \end{matrix}

Egyensúlyi állapotban az elnyelt és a kisugárzott teljesítmény megegyezik:

\begin{matrix} P_{elnyelt} = P_{kisugárzott}, \end{matrix}

ahonnan a szonda hőmérsékletére

\begin{matrix} T_{szonda} = T_{Nap} \cdot \sqrt[]{\frac{R_{Nap}}{2 R}} \approx 289 K \end{matrix}

adódik.

2. Ha a szonda felülete olyan, hogy csak egy bizonyos

f_{max}

frekvencia alatt nyel el (és ugyanekkora frekvenciáig sugároz) elektromágneses hullámokat, akkor valamely

T

hőmérsékleten az elnyelt (és a leadott) teljesítmény a feketetestéhez képest

\begin{matrix} \frac{15}{π^{4}} \cdot \int_{0}^{η_{max}} \frac{η^{3} d η}{e^{η} - 1} \end{matrix}

faktorral változik meg, ahol

η_{max} = (h f_{max}) / (k T)

. A fenti képlet azt adja meg, hogy a Planck-féle sugárzási törvényben szereplő függvény nulla és bizonyos

f_{max}

értékek közötti görbe alatti területe hányadrésze a teljes görbe alatti területnek.
A Nap

T = 6000

K-es hőmérsékleténél

η_{max} = 1200 K/6000 K= 0,2

nagyságú, vagyis az elnyelt sugárzás kiszámításánál a Planck-görbének csak az origóhoz közeli kicsiny darabja kap szerepet.

\begin{matrix} \int_{0}^{η_{max}} \frac{η^{3} d η}{e^{η} - 1} \approx \int_{0}^{η_{max}} \frac{η^{3} d η}{(1 + η) - 1} = \int_{0}^{η_{max}} η^{2} d η = \frac{η_{max}^{3}}{3} . \end{matrix}

A szonda tehát a festékréteg fényvisszaverő tulajdonságai miatt

\begin{matrix} \frac{15}{π^{4}} \cdot \frac{0, 2^{3}}{3} \approx 4, 1 \cdot 10^{- 4} - szer kevesebb \end{matrix}

energiát nyel el, mint ha feketetest lenne. Ha egy pillanatra elfeledkezünk arról, hogy a kisugárzott teljesítmény is kisebb, mint egy abszolút fekete testé, akkor a hőmérsékletre a

\begin{matrix} 4, 1 \cdot 10^{- 4} r_{szonda}^{2} π \cdot σ T_{Nap}^{4} \cdot \frac{R_{Nap}^{2}}{R^{2}} = 4 π r_{szonda}^{2} \cdot σ T_{szonda}^{4} \end{matrix}

összefüggésből

\begin{matrix} T_{szonda} = {(4, 1 \cdot 10^{- 4})}^{1 / 4} \cdot T_{Nap} \cdot {(R_{Nap} / R)}^{1 / 2} = 4, 1 K \end{matrix}

értéket kapjuk.
Vajon mekkora hibát követtünk el akkor, amikor a kisugárzott teljesítmény számításánál a teljes frekvencia-tartományt figyelembe vettük, s nem csak az

f_{max}

alatti értékeket? Mivel

T = 41

K-nél

η_{max} = 1200 K/41 K\approx30

, másrészt a Planck-görbe grafikonjáról leolvasható, hogy a kisugárzott teljesítmény gyakorlatilag teljes egészében az

η < 10

frekvenciatartományból származik, a közelítésünk jogossága utólag beigazolódott.

3. A

0, 5

m sugarú űrszonda által elnyelt teljesítmény

\begin{matrix} 4, 1 \cdot 10^{- 4} \cdot σ T_{Nap}^{4} \cdot r_{szonda}^{2} π \cdot {(R_{Nap} / R)}^{2} \approx 0, 5 W. \end{matrix}

Mivel ez az érték sokkal kisebb, mint a belső hőtermelés

P_{0} = 1

kW-os teljesítménye, elegendő az utóbbival számolnunk. A

P_{0}

-hoz tartozó ,,feketetest-hőmérséklet''

\begin{matrix} T_{fekete szonda} = {(\frac{P_{0}}{4 π {r^{2}}_{szonda} σ})}^{1 / 4} = (\frac{1, 0 \cdot 10^{3} W\cdotm^{2}K^{4}}{4 π \cdot {0, 5}^{2} m^{2}\cdot5,7\cdot10^{- 8} W}) \approx 270 K, \end{matrix}

ekkora lenne a szonda hőmérséklete, ha minden frekvencián képes lenne sugározni. Mivel azonban ekkora hőmérsékleten

η_{max} = 4, 4

és a Planck-görbe ezen

η_{max}

alatti tartományának területe kb. az egész terület

70

százaléka, a tényleges hőmérsékletnek magasabbnak kell lennie, mint a feketetest-hőmérséklet.
A pontos egyenlet, amelyből az egyensúlyi hőmérséklet megkapható:

\begin{matrix} P_{0} = 4 π r_{szonda}^{2} \cdot σ T_{szonda}^{4} \cdot \frac{15}{π^{4}} \cdot \int_{0}^{\frac{1200 K}{T_{szonda}}} \frac{η^{3} d η}{e^{η} - 1} . \end{matrix}

Találgatással

-

és a görbe alatti területek numerikus összeszámolásával

-

megkaphatjuk, hogy az

1

kW-os hőtermelésű szonda kb.

310 K\approx40^{\circ}C

hőmérsékletű.

4. A hőtan II. főtétele szerint nem létezhet olyan festék, amely egy bizonyos frekvencia-tartományban nem nyel el sugárzást, de ugyanakkor feketetestként sugároz ebben a frekvencia-tartományban. Ha ugyanis létezne ilyen anyag, akkor tudnánk készíteni egy olyan zárt rendszert, melynek részei kezdetben azonos hőmérsékletűek, majd a sugárzási energiaátadás következtében a rendszer egyik része lehűlne, a másik pedig felmelegedne!

5. Olyan borítás, amely a földi légkörhöz hasonlóan a magasabb frekvenciájú sugárzást átengedi, az alacsonyabb frekvenciájúakat viszont visszaveri, ,,üvegházhatást'' hoz létre és a feketetest-hőmérséklet fölé emeli a szonda hőmérsékletét. Ha például a korábban említett

1200

K-nek megfelelő frekvencia a küszöbérték, de a festék áteresztőképessége éppen a fordítottja a 2. alpontbelinek, akkor egy

289

K-es szonda gyakorlatilag ugyanannyi energiát nyel el, mintha feketetest lenne, viszont

η_{min} = 1200 K/289 K\approx4

miatt sugározni csak kb. feleannyira tud, mint egy feketetest. A szonda tehát felmelegszik, egészen addig, amíg az elnyelt és a kisugárzott teljesítmény egyenlő nem lesz egymással.

Mérési feladatok

1. feladat: A levegő átütési feszültségének vizsgálata

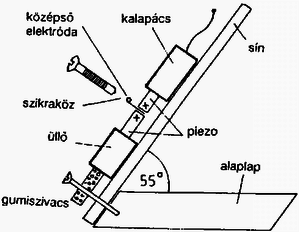1. ábra

Ebben a mérésben a terem levegőjének átütési feszültségét fogod tanulmányozni piezoelektromos anyagdarabok által létrehozott nagyfeszültség segítségével. A kísérleti eszköz egy sínből és egy rajta lecsúsztatható

m

tömegű ,,kalapácsból'' áll (1. ábra). A lecsúszó kalapács nekiütközik a két hengeres darabból összetett piezo-rendszernek, amely így kissé összenyomódik. A testek (,,piezok'') összenyomódása következtében azok végei elektromosan feltöltődnek. Az így keletkező elektromos feszültséget egy állítható résre (szikraközre) vezetjük. Ha a rés szélessége elegendően kicsi, akkor egy szikra üt át a résen. A szikra szabad szemmel is látható. Ha azonban a rés túl széles, akkor nincs szikra. A legkisebb olyan feszültséget, amely még szikrát kelt az adott résen, a rés átütési feszültségének hívjuk.
Határozd meg az átütési feszültséget a rés szélességének függvényében! Becsüld meg az eredmények hibáit, tárgyald a különböző hibaforrásokat, azok természetét! Tárgyald azt is, hogy érvényes-e általában ez az eredmény más kisütési körülmények között is! A dolgozatodban ismertesd

$-$	a mérési módszeredet,

$-$	röviden írd le, hogyan oldottad meg a mérés során felmerülő gyakorlati finomságokat,

$-$	tüntesd fel dolgozatodban a piezopáron látható azonosító számot!

A piezoelektromosság elmélete

A piezoelektromos anyagok teljes elméletére itt nincs szükségünk; a következő egyszerű modell elegendő lesz.
A piezo-testet (,,piezot'') egy mechanikus rugóval és egy elektromos kondenzátorral modellezhetjük. A hengeres test alap- és fedőlapja a kondenzátor két lemeze. Ha a rugót (azaz a testet) összenyomjuk, az összenyomás hatására elektromos töltés távozik az egyik lemezről, és töltés kerül a másik lemezre, s ezáltal feszültség jelenik meg a kondenzátoron. A töltés nagysága arányos az össszenyomás mértékével. A folyamat megfordítható: az összenyomó erő csökkentésével a töltések az ellenkező irányba vándorolnak.
Tekintsük sorrendben a következő (1), (2) és (3) események egymásutánját egy

C

kapacitású piezoval:
(1) Erővel hatunk a piezora,
(2) a piezot egy vezetővel rövid ideig rövidre zárjuk,
(3) az összenyomó erőt megszüntetjük.

Ekkor (1) során

Q

töltés kerül a lemezekre, és

U = Q / C

feszültség jelenik meg a piezo két oldala között. (2)-ben a feszültség leesik

U = 0

-ra; majd (3) során egy ellenkező előjelű

- U

feszültség jelenik meg.
Jelöljük a piezo kapacitást most

C_{p}

-vel. Ha egy kezdetben töltetlen és nem összenyomott piezot megnyomunk úgy, hogy közben a nyomóerő

E

mechanikai munkát végez, akkor

K \cdot E

nagyságú energia alakul át elektromos energiává, és ez a

C_{p}

kapacitású kondenzátor elektromos energiája lesz. A

K

állandó értéke a piezo anyagától függ; a jelen mérésnél használt piezo esetében az anyag gyártója a

K = 0, 5

értéket adta meg.

A mérésről

A készüléket úgy állították össze, hogy az összenyomás hatására pozitív töltés jelenik meg a piezoknak az ábrán ,,+'' jellel jelölt végein. A ,,+'' végeket egymással és a középső elektróddal összekötöttük, ez az elektród lesz a szikraköz egyik oldala.
A készülék elrendezése olyan, hogy a kalapács a felső piezo felső végével elektromos kontaktusba kerül, és így összeköti a piezot a fémsínnel is.
A piezopár alatt egy ,,üllő'' van. Az összenyomó erőt a kalapács és az üllő együttes hatása hozza létre. Az üllő egy gumiszivacs-darabkával van alátámasztva, így az üllő az ütközés során nem képes hirtelen impulzust átadni az állványzatnak. Az üllő összeköti az alsó piezo alsó lapját a fémsínnel. A fémsínt egy rézdróttal kötheted össze a szikraköz másik oldalát képező állítható csavarral.
A sínen egy gumilapocska is van, amely kb.

10

cm-ben korlátozza a kalapács úthosszát. Ne lépd túl ezt a határt! Fordulj a rendezőkhöz, ha egyáltalán nem sikerül szikrát megfigyelned!
Kétféle módszerrel is észlelheted a szikrákat:

(i)	Figyeld meg szabad szemmel a szikrákat! Ehhez az állítócsavart a sínnel össze kell kötni (,,földelni kell'').

(ii)	Érzékelheted a szikrát az ujjaddal is, ekkor nem lehet földvezeték a csavaron. Egyik ujjaddal érintsd meg a csavart, másikkal pedig a csúszósínt. A szikra árama ekkor a kezeden halad át, s érezheted, hogy volt-e kisülés vagy sem.

Bármelyik ‐ általad jobbnak ítélt ‐ módszert használhatod, sőt mindkettőt is.
A csúsztató készüléken kívül egy háromszögvonalzó, egy kis csavarhúzó és néhány milliméter-papír is rendelkezésedre áll.

Adatok:

$-$	a nehézségi gyorsulás Finnországban: $g = 9, 82$ m/s $^{2}$ ,

$-$	a piezok kapacitása egyenként: $C_{p} = (20 \pm 2)$ pF,

$-$	a kalapács tömege: $m = 34, 6$ g,

$-$	az üllő és a két piezo tömege együtt: $M = (87, 5 \pm 0, 5)$ g,

$-$	a szikraköz nagyságát állító csavar menetemelkedése fordulatonként: $0, 8 mm$ ,

$-$	a csúszósínnek a függőlegessel bezárt szöge: $35^{\circ}$ .

Megjegyzések.

(i)	A piezo-kapacitás szivárgási árama rendkívül kicsi, így a kondenzátor nagyon sokáig megőrzi töltését. Vedd figyelembe ezt a tényt a mérésed megtervezésekor!

(ii)	A piezo által keltett elektromos töltés olyan kicsi, hogy nem veszélyes az emberre. A szikra nem ráz meg, de érezheted azt.

(iii)

Van egy kis esélye annak, hogy az ismétlődő ütésektől a piezo darabokra törik. Ha ez megtörténne, szólj a rendezőknek. Vannak tartalék piezok is. A törés elkerülése érdekében minden egyes ütés előtt győződj meg róla, hogy a piezopár jól fekszik a síneken, és biztosan hozzáér az üllőhöz. A kalapácsot az elengedése előtt a fonalnál fogva tartsd, így az simán, ugrálás nélkül fog lecsúszni.

(iiii)

A szikraköz kapacitása olyan kicsi, hogy nem kell figyelembe venned!

(iiiii)

A kalapács és az üllő merev testeknek tekinthetők, amelyek az ütközés alatt nem nyomódnak össze.

Megoldás. A kalapács

α

hajlásszögű lejtőn

\begin{matrix} a = g (sin α - μ cos α) \end{matrix}

gyorsulással mozog. (Itt

μ

a csúszási súrlódási együtthatót jelöli, ennek értékét a lejtő megdöntésével és az

α_{0}

csúszási határszög mérésével lehet becsülni:

tg α_{0} = μ

.) A kalapácsot az alsó helyzetétől mért

s

távolságból indítva, az

v = \sqrt[]{2 a s}

sebességgel csapódik a piezoknak. Az

m

tömegű kalapács az

M

tömegű piezo + üllő rendszernek ütközik, és a legnagyobb deformáció pillanatában közös

V

sebességgel mozognak. Tekintettel arra, hogy a gumiszivacs az ütközés rövid ideje alatt nem képes számottevő impulzus átadásra, a két test összimpulzusa megmarad:

\begin{matrix} m v = (m + M) V, \end{matrix}

ahonnan a deformációs energiára

\begin{matrix} E = \frac{1}{2} (m + M) V^{2} - \frac{1}{2} m v^{2} = \frac{1}{2} \frac{m M}{m + M} v^{2} = \frac{m M}{m + M} g s (sin α - μ cos α) \end{matrix}

adódik. A rugalmas energia

K

-szorosa átalakul a

2 C_{p}

kapacitású piezo-pár elektrosztatikus energiájává:

\begin{matrix} K \cdot E = \frac{1}{2} \cdot 2 C \cdot U^{2}, \end{matrix}

ahonnan

U

kiszámítható az

s

indítási távolság függvényeként.
A mikrométer-csavar elfordulásainak számából és a menetemelkedés megadott értékéből pontosan meghatározhatjuk a szikraköz nagyságát, és az éppen megjelenő szikrához tartozó feszültség a keresett átütési feszültség. Egy bizonyos beállított

d

szikraköznél fokozatosan növelve

s

-t és kiszámolva a szikra megjelenésekor mért

s

-hez tartozó

U

értéket, megkapjuk a keresett

U (d)

függvény egyes pontjait. Fontos, hogy minden egyes ütköztetés előtt a földelő vezeték segítségével ,,kisüssük'' a piezot, eltávolítsuk a rajta maradt töltéseket.
A mérési eredményekből adódó

U (d)

függvény nem univerzális, menete számos körülménytől (például az elektródák alakjától, a levegő hőmérsékletétől és páratartalmától stb.) függhet.

2. feladat: Optikai rács és optikai szűrők

A következő eszközök állanak rendelkezésedre:

$-$	Egy kis zseblámpa;

$-$	Egy nem - hagyományos optikai rács, műanyag kockához rögzítve. Ennek a rácsnak a barázdái körív alakúak, így a reflektált fény a szokásos rácsokétól eltérően némileg torzított.

$-$	Néhány műanyag játékkocka, amelyet állványként használhatsz;

$-$	néhány optikai eszköz: (1) (piros), (2) (piros), (3) (kék), (4) (rózsaszín), (5) (lila), (6) (szürke), (7) (fehér);

$-$	Három milliméter-papír;

$-$	Papírdoboz, amelyre elhelyezheted a mérőeszközöket.

1. Határozd meg az optikai rács rácsállandóját amilyen pontosan csak lehetséges! Becsüld meg a mérés hibáját! Írd le a mérés elvét, és az általad alkalmazott mérési elrendezést! Mindezeket rajzold is le! Add meg a közvetlenül mért adatokat, a mérési eredményeket a hibákkal együtt, és magyarázd meg, hogyan kaptad meg a végeredményeket!

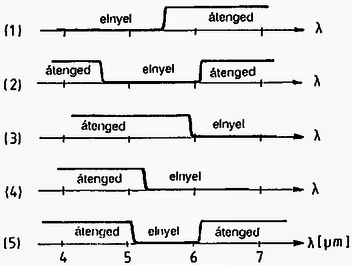
2. Az (1)‐...‐(5) jelű optikai eszközök színszűrők. Milyen hullámhosszúságú fényt engednek át, és milyent nyelnek el? Ahol lehet, adjál meg numerikus értékeket hibabecsléssel együtt; egyébként eredményeidet grafikusan ábrázold!
Derítsd ki, hogy micsoda a (6) jelű eszköz!

3. A (7) jelű eszköz egy drótháló. Határozd meg ezen háló drótszálainak távolságát mindkét, egymásra merőleges irányban! Rajzold le, milyen mérési elrendezést alkalmaztál!
A látható fény hullámhosszai

0, 4 \cdot 10^{- 6}

m és

0, 7 \cdot 10^{- 6}

m közé esnek.

Figyelem: A zseblámpa elemei nem örökéletűek! Kb. 40 perc alatt a fény láthatóan halványabbá és vörösebbé válik. Kapcsold ki a lámpát, ha nem használod!

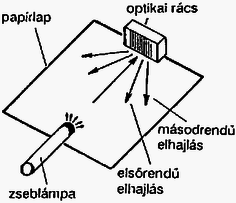1. ábra

Megoldás. 1. Állítsuk össze az 1. ábrán látható mérési elrendezést! Nézzünk a rácsra majdnem pontosan a zseblámpa irányából, de kicsit messzebbről, a zseblámpa mögül. A visszavert fény felhasználásával könnyen beállíthatjuk a rácsot úgy, hogy éppen a beeső fényre merőlegesen álljon. Ezután szabad szemmel figyeljük meg az elhajló nyalábokat (különböző színű foltokat látunk), és jelöljük be a papírlapon a fényutak irányát, majd mérjük le (és trigonometria segítségével számítsuk ki) az elhajlások

α

szögét.
Az elhajlásra vonatkozó Bragg-egyenlet:

\begin{matrix} d = k λ / sin α, \end{matrix}

ahol

d

a keresett rácsállandó,

k = 1, 2, 3, ...

az elhajlás rendje,

λ

pedig a vizsgált fény hullámhossza. Ábrázoljuk a különböző színekre (a látható fény spektrumának szélén elhelyezkedő kékre, illetve vörösre)

k λ

-t

sin α

függvényében. A kapott pontokra egyenest illesztve, annak meredeksége éppen a

d

rácsállandót adja. A leolvasási bizonytalanságot és a hullámhossz-adatok pontatlanságát figyelembe véve eredményül

d = 1, 7 μ m \pm 0, 1 μ m

adódik.
2. Most is az előző alkérdés kísérleti elrendezését használhatjuk. Az (1)‐(5) jelű szűrőket egyenként a fényútba helyezve megmérhetjük, hogy az egyes szűrők milyen hullámhosszúságú fényt engednek át. Az eredmények vázlatosan a következők:

A (6) jelű elem egy polárszűrő. Erről úgy győződhetünk meg, hogy ha a szűrőn keresztül egy tárgyról (pl. az ablaküvegről, vagy a tartóállványként használt játékkockáról) visszavert (és emiatt részlegesen polarizált) fényt nézzük, és a szűrőt a síkjában forgatjuk, akkor változik a fény intenzitása.
3. Helyezzünk a zseblámpa elé színszűrőt (azért, hogy a spektrumot szűkítsük), majd tegyük a (7) jelű elemet (amely egy finom szövésű drótháló) merőleges helyzetben a lámpából a szemünkbe érkező fény útjába (2. ábra).

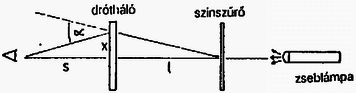2. ábra

3. ábra

Ekkor az első- és másodrendű elhajlások miatt a 3. ábrán látható képet kapjuk. A kis eltérülési szögek miatt

\begin{matrix} α \approx \frac{x}{l} + \frac{x}{s}, \end{matrix}

tehát

s, l

és

x

mérésével

λ

ismeretében a

d

rácsállandó számítható. Eredményül mindkét irányban

d = 70 μ m \pm 10 μ m

adódik és az is látszik, hogy a kétféle irányú drótköteg szálai merőlegesek egymásra.