Cím:	1991-92. évi fizika OKTV II. fordulójának feladatai
Szerző(k):	Holics László ,  Honyek Gyula ,  Szegedi Ervin
Füzet:	1992/november, 401 - 410. oldal	PDF  |  MathML
Témakör(ök):	OKTV

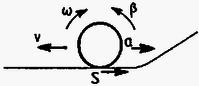
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1991/92. évi fizika OKTV második fordulójának feladatai 1   I. kategória (szakközépiskolások)   1. Egy vízszintes érdes és egy hozzá törésmentesen csatlakozó lejtőből álló merev felületen $v_0=3\mathrm{,}5\text{m/s}$ sebességgel csúszásmentesen gördül egy $r=0\mathrm{,}1\text{m}$ sugarú vékony abroncs a lejtő felé, merőlegesen a vízszintes síkkal való érintkezési vonalára. a) Mikor jut magasabbra az abroncs, ha a lejtőn van súrlódás, vagy ha nincs? b) Ha lejtős rész ideálisan sima, a róla visszaérkező abroncs milyen távol lesz a lejtő aljától az odaérkezéstől számított $t=2\mathrm{,}4\text{s}$ múlva?     (A vízszintes sík és az abroncs közötti súrlódási együttható ${\mu }_0=\mu =0\mathrm{,}2$, a lejtő a síkhoz $R>r$ görbületi sugarú hajlattal csatlakozik, az abroncs a mozgása során nem dől el.) (Holics László)   Megoldás. a) Az abroncs akkor jut magasabbra, ha van súrlódás, mert ebben az esetben a forgási energiájának egy része (esetleg az egésze) is átalakul helyzeti energiává (más szóval az abroncs felfelé haladtában csökken tömegközéppontjának sebessége, így felfelé mutató $-$ szögsebességet csökkentő $-$ súrlódási erő is hat rá, ami emeli az abroncsot!). Érdekes, hogy amennyiben az abroncs mindvégig tapad (csúszásmentesen gördül), akkor feljut $\begin{array}{c}{\displaystyle \Delta h_1=\frac{E_{\text{kin}}}{mg}=\frac{\frac{1}{2}m{v}_0^2+\frac{1}{2}{\Theta }_s{\omega }^2}{mg}=\frac{v_0^2}{g}}\end{array}$ magasra, míg ha nincs súrlódás, csak $\begin{array}{c}{\displaystyle \Delta h_2=\frac{E_{\text{<span style="font-weight: normal;font-style: normal;">haladó</span>}}}{mg}=\frac{\frac{1}{2}m{v}_0^2}{mg}=\frac{v_0^2}{2g}}\end{array}$ magasságig ér fel. A két magasság aránya abroncs esetén $\begin{array}{c}{\displaystyle \frac{\Delta h_1}{\Delta h_2}=2.}\end{array}$ (Megjegyezzük, hogy gömb esetén ugyanez az arány $7/5=1\mathrm{,}4$.) Ha a lejtőn kicsi a súrlódás, köszörülve emelkedik a golyó és $\Delta h$ emelkedési magasságára: $\begin{array}{c}{\displaystyle \Delta h_2<\Delta h<\Delta h_1}\end{array}$ ilyenkor az energia egy része disszipálódik. b) Amikor az abroncs eléri a lejtőt, ha $r<R$, ütközés nélkül gördül fel rajta. 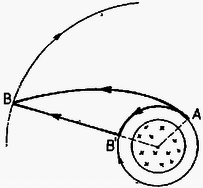Odaérkezéskor középpontjának sebessége $v_0$, szögsebessége pedig $\begin{array}{c}{\displaystyle {\omega }_0=\frac{v_0}{r}\mathrm{.}}\end{array}$     A lejtőn súrlódás híján (mivel így az abroncsra külső forgatónyomaték nem hat) a sajátperdület és ezzel a szögsebesség mindvégig megmarad. Az abroncs felcsúszik $\begin{array}{c}{\displaystyle \frac{v_0^2}{2g}}\end{array}$ magasra, ahol sebessége zérussá válik, majd visszacsúszik a lejtő aljára, ahová ismét $v_0$ nagyságú, de ellenkező irányú sebességgel érkezik, miközben forgási iránya nem változik meg. Így a vízszintes síkra visszaérkező abroncs köszörülve kezdi meg mozgását, amely köszörülés mindaddig tart, míg a súrlódási erő forgatónyomatéka szögsebességét az aktuális sebességgel összehangolva $\omega =v/r$ nagyságúra és megfelelő irányúra nem állítja be. (Ez elvileg lehetséges úgy is, hogy megfordítja a forgásirányt, de úgy is, hogy a sebességet fordítja meg, speciálisan mindkettőt egyszerre zérusra csökkentheti. Mint kiderül, ez a tehetetlenségi nyomaték nagyságától függ. 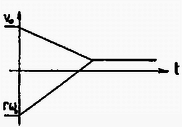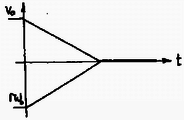A feladathoz tartozik ennek a vizsgálata.) A három eset grafikus jellemzése ($t=0$ a leérkezés pillanata):             Számítások: A vízszintes síkra visszacsúszott abroncs tömegközéppontjának gyorsulása: $\begin{array}{c}{\displaystyle a=\mu g=\text{const}\mathrm{.}}\end{array}$ Az abroncs szöggyorsulása $\begin{array}{c}{\displaystyle \beta =-\frac{\mu mgr}{m{r}^2}=-\frac{\mu g}{r}=\text{const}\mathrm{.}}\end{array}$ Az abroncs központjának mindenkori sebessége az idő függvényében: $\begin{array}{c}{\displaystyle v=-v_0+\mu gt\mathrm{,}}\end{array}$ szögsebessége: $\begin{array}{c}{\displaystyle \omega ={\omega }_0-\frac{\mu g}{r}t\mathrm{.}}\end{array}$ A csúszás $t_1$ idő múlva befejeződik, amelyre fennáll, hogy $\begin{array}{c}{\displaystyle -v_0+\mu g{t}_1={\omega }_{0}r-\mu g{t}_1\mathrm{,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle 2\mu g{t}_1=2v_0}\end{array}$ és $\begin{array}{c}{\displaystyle t_1=\frac{v_0}{\mu g}=\frac{3\mathrm{,}5}{2}\text{<span style="font-weight: normal;font-style: normal;">s</span>}=1\mathrm{,}75\text{s. }}\end{array}$ Az abroncs középpontjának sebessége ekkor $\begin{array}{c}{\displaystyle v=-v_0+\mu g\frac{v_0}{{\mu }_{0}g}=\mathrm{0,}}\end{array}$ vagyis éppen azzal a speciális esettel állunk szemben, amelyben az abroncs akkor áll meg, amikor szögsebessége is nullára csökken, s így nem fordul meg sem a sebessége, sem a szögsebessége a visszaút során. Az abroncs tehát $2\mathrm{,}4\text{s}$ múlva ugyanott lesz, ahol $1\mathrm{,}75\text{s}$ múlva volt, vagyis a lejtő aljától számítva a vízszintes síkon $\begin{array}{c}{\displaystyle s=-v_0{t}_1+\frac{1}{2}\mu g{t}_1^2=-3\mathrm{,}0625\text{m=-306 }\text{cm }}\end{array}$ koordinátájú pontban. (Az origó a lejtő aljánál van, a pozitív $x$-ek a lejtő alatt helyezkednek el.)   Megjegyzés. Tömör gömb esetén annyival komplikáltabb a helyzet, hogy az egy idő után ismét tisztán gördül (a szögsebessége vált irányt), és a megadott időn belül egy lassuló és egy egyenletes mozgásszakasza van. $\omega =0$, ha $\begin{array}{c}{\displaystyle t_1=\frac{2}{5}\frac{v_0}{\mu g}=0\mathrm{,}7\text{s, }}\end{array}$ a sebessége ekkor $\begin{array}{c}{\displaystyle v=v_0-\mu g{t}_1=2\mathrm{,}1\text{m/s, }}\end{array}$ tehát eddig csúszva gördült, ettől kezdve tiszta gördüléssel egyenletesen mozog. Csúszva megtesz $\begin{array}{c}{\displaystyle s_{\text{<span style="font-weight: normal;font-style: normal;">csúsz</span>}}=v_0{t}_1-\mu g{t}_1=1\mathrm{,}96\text{m }}\end{array}$ utat, míg tisztán gördülve a $2\mathrm{,}4$ s elteltéig $\begin{array}{c}{\displaystyle s_{\text{tisz}}=v\left(t-t_1\right)=3\mathrm{,}57\text{m }}\end{array}$ utat, összesen tehát $s=5\mathrm{,}53$ m-re kerül a lejtő aljától. Olyan eset, hogy visszafelé (ismét a lejtő felé) induljon meg egy hengerszimmetrikus test, csak akkor fordulhat elő, ha az abroncsénál is nagyobb a tehetetlenségi nyomatéka a forgástengelyére nézve (pl. egy orsó gördülne föl egy, a kerekei által közrefogott sínen).   2. Határozzuk meg a levegő fajhőjét annak ismeretében, hogy a levegő összetétele tömegszázalékban $75\mathrm{,}5\%$ nitrogén, $23\mathrm{,}2\%$ oxigén és $1\mathrm{,}3\%$ argon. A nitrogén, oxigén és argon atomtömege rendre $14\text{<span style="font-weight: normal;font-style: normal;">ATE</span>}\mathrm{,}16\text{<span style="font-weight: normal;font-style: normal;">ATE</span>}$ és $40\text{<span style="font-weight: normal;font-style: normal;">ATE</span>}$. (Holics László)   Megoldás. A gázkeverék átlagos, állandó térfogathoz tartozó fajhőjének meghatározása az $E=c_{v}mT$ összefüggés és az energia additivitása ($E=E_1+E_2+E_3$) alapján $\begin{array}{c}{\displaystyle c_{v_k}mT=c_{v_1}{m}_{1}T+c_{v_2}{m}_{2}T+c_{v_3}{m}_{3}T=c_{v_1}{\alpha }_{1}mT+c_{v_2}{\alpha }_{2}mT+c_{v_3}{\alpha }_{3}mT\mathrm{,}}\end{array}$ végül $mT$-vel való egyszerűsítés után: $\begin{array}{c}{\displaystyle c_{v_k}={\alpha }_1{c}_{v_1}+{\alpha }_2{c}_{v_2}+{\alpha }_3{c}_{v_3}\mathrm{.}}\end{array}$ (Ez valójában a százalékokkal súlyozott számtani közép: $\begin{array}{c}{\displaystyle c_{v_k}=\frac{{\alpha }_1{c}_{v_1}+{\alpha }_2{c}_{v_2}+{\alpha }_3{c}_{v_3}}{{\alpha }_1+{\alpha }_2+{\alpha }_3}\mathrm{,}}\end{array}$ ahol ${\alpha }_1+{\alpha }_2+{\alpha }_3=1$.) A fajhő ismert molekuláris kifejezésével: ${\displaystyle \begin{array}{c}\hfill {\displaystyle c_{v_k}={\alpha }_1\frac{f_1}{2}\frac{R}{M_1}+{\alpha }_2\frac{f_2}{2}\frac{R}{M_2}+{\alpha }_3\frac{f_3}{2}\frac{R}{M_3}=}\hfill \\ \hfill {\displaystyle =\left(0\mathrm{,}755\cdot \frac{5}{2}\cdot \frac{1}{28}+0\mathrm{,}232\cdot \frac{5}{2}\cdot \frac{1}{32}+0\mathrm{,}013\cdot \frac{3}{2}\cdot \frac{1}{40}\right)\cdot 8\mathrm{,}31\frac{\text{kJ}}{\text{kgK}}=714\mathrm{,}85\frac{\text{J}}{\text{kgK}}\mathrm{.}}\hfill \end{array}}$ (A mi levegőnkben nem volt szén-dioxid, ezért kissé eltér a függvénytáblázatbeli adattól, amely $712\text{J/(kgK)}$ értéket ad meg.)   3. Egy hosszú, vékony, $R=2\text{cm}$ sugarú egyenes tekercs belsejeben a mágneses indukció értéke $\Delta t={10}^{-1}\text{s}$ alatt $B=0\mathrm{,}8\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>V</mi><mi>s</mi><mo stretchy="false">/</mo><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$ értékről egyenletesen $0$-ra csökken. a) Mekkora gyorsulással indul a tekercs tengelyétől $r_A=3\text{cm}$-re levő $A$ pontban nyugvó elektron? b) Mekkora sebességre tesz szert az elektron, mialatt a pályasík és a tekercstengely közös pontjából nézve $\phi ={120}^{\circ }$-os látószögű pályaszakaszon végigfutva a $B$ pontba kerül?     (Holics László)   Megoldás. a) Az elektron gyorsulása az indukált elektromos mező térerősségének és az elektron fajlagos töltésének szorzatával egyenlő. Az elektromos térerősséget az örvényerősség (nyugalmi indukció) törvényéből határozhatjuk meg: $\begin{array}{c}{\displaystyle \sum _{}^{\circ }E\Delta s\text{cos}\alpha =-\frac{\Delta \Phi }{\Delta t}\mathrm{.}}\end{array}$ Ha az $r_A$ sugarú kör mentén számítjuk az örvényerősséget (körfeszültséget), $\text{cos}\alpha =1$ és az elektromos térerősség nagysága állandó, tehát $\begin{array}{c}{\displaystyle E\cdot 2r_A\pi =\frac{\Delta \Phi }{\Delta t}\mathrm{.}}\end{array}$ Innen az elektromos térerősség az elektron kiindulási pontjában: $\begin{array}{c}{\displaystyle E_A=\frac{1}{2r_A\pi }\frac{\Delta \Phi }{\Delta t}\mathrm{.}}\end{array}$ Az elektromos mezőt létrehozó mágneses fluxusváltozás $\Delta \Phi =A\Delta B$ nagyságú, a tekercs sugarával kifejezve: $\begin{array}{c}{\displaystyle \Delta \Phi =R^2\pi \Delta B\mathrm{.}}\end{array}$ Az elektron gyorsulása ezekkel: $\begin{array}{c}{\displaystyle a=\frac{F}{m}=\frac{eE}{m}=\frac{e}{m}\frac{R^2\Delta B}{2r_A\Delta t}\mathrm{.}}\end{array}$ Számadatokkal: $\begin{array}{c}{\displaystyle a=\frac{1\mathrm{,}6\cdot {10}^{-19}\text{As<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math>4<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>10</mn></mrow><mrow><mo stretchy="false">-</mo><mn>4</mn></mrow></msup></mrow></math> }\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math>0,8 }\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>V</mi><mi>s</mi><mo stretchy="false">/</mo><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}}{9\mathrm{,}1\cdot {10}^{-31}\text{kg<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math>2<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math>3<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>10</mn></mrow><mrow><mo stretchy="false">-</mo><mn>2</mn></mrow></msup></mrow></math> }\text{m<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>10</mn></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math> }\text{s}}\approx 9\mathrm{,}38\cdot {10}^9\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi><mo stretchy="false">/</mo><mi>s</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>. }}\end{array}$ b) Az elektron sebességét az indukált mező munkája szabja meg. A problémát az okozza, hogy az $A$ ponton áthaladó elektromos erővonalról ,,kisodródik'' az elektron, és sem a pályája, sem a pálya mentén mérhető elektromos térerősség nem határozható meg elemi úton.     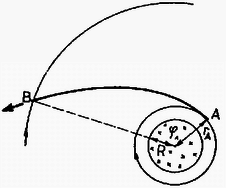Az indukált elektromos mező időben állandó, és nem konzervatív, potenciál (feszültség) nem értelmezhető benne. A körfeszültség azonban mindazon görbén számolva, amely nem vesz körül mágneses fluxusváltozást, zérus. Így ha sikerül az elektron tényleges pályagörbeszakaszát olyan zárt görbévé kiegészítenünk, amely nem vesz körül változó mágneses fluxust és a kiegészítő szakaszon könnyen meghatározható a mező munkája, az ismeretlen pályagörbén végzett munkát is meghatározhatjuk elemi úton. Ilyen kiegészítő görbe az ábrán látható azonos látószögű, a tekercs tengelyével koncentrikus körívből és sugár irányú egyenesszakaszból álló vonal. Ennek az első szakaszán, az $AB\text{'}$ köríven végzett elektromos munka: $\begin{array}{c}{\displaystyle W_{\text{el}}=F\cdot s=eE{r}_A\phi =e\frac{1}{2r_A\pi }\frac{\Delta \Phi }{\Delta t}\cdot r_A\phi =e\frac{1}{2r_A\pi }\frac{R^2\pi \Delta B}{\Delta t}{r}_A\phi =\frac{e{R}^2\phi \Delta B}{2\Delta t}\mathrm{,}}\end{array}$ függetlenül az elektron kiindulási $A$ pontjának a tengelytől való $r_A$ távolságától. A második, sugárirányú $BB\text{'}$ szakaszán végzett munka nulla! Ugyancsak $W_{\text{el}}$-nek kell lennie az $AB$ valódi pályán végzett munkának is. Ezzel az elektron sebessége (feltételezve, hogy a folyamat vákuumban megy végbe) a munkatétel alapján: $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}^2=W_{\text{el}}}\end{array}$ egyenletből $\begin{array}{c}{\displaystyle v=\sqrt[]{\frac{e}{m}\frac{R^2\Delta B}{\Delta t}\phi }\mathrm{,}}\end{array}$ számértékeinkkel: $\begin{array}{c}{\displaystyle v=\sqrt[]{\frac{1\mathrm{,}6\cdot {10}^{-19}\text{As<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math>4 <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>10</mn></mrow><mrow><mo stretchy="false">-</mo><mn>4</mn></mrow></msup></mrow></math> }\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math>0,8 }\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>V</mi><mi>s</mi><mo stretchy="false">/</mo><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}}{9\mathrm{,}1\cdot {10}^{-31}\text{kg<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>10</mn></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math> }\text{s}}\cdot \frac{2\pi }{3}}\approx 34\mathrm{,}3\text{km/s. }}\end{array}$   Megjegyzés. Eredményünket a $AB\text{'}$ köríven kényszermozgással haladó (egyenletesen gyorsuló körmozgást végző) elektron sebességképletével is megkaphatjuk: $\begin{array}{c}{\displaystyle v=\sqrt[]{2as}=\sqrt[]{2\frac{eE}{m}r\phi }=\sqrt[]{\frac{e{R}^2\Delta B}{m\Delta t}\phi }\mathrm{.}}\end{array}$   II. és III. 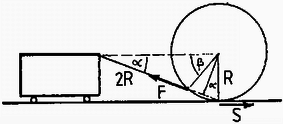kategória (valamennyi gimnazista)   1. Egy $R$ sugarú, homogén, tömör, $m$ tömegű korongot pereméhez erősített $2R$ hosszúságú fonállal vízszintes síkon állondó sebességgel vontat egy kocsi, amelyhez a talajtól mért $R$ magasságban erősítették a fonál másik végét. Egyensúly esetén mekkora szöget zár be a vízszintessel a fonál, ha a) nincs súrlódás, b) ha van? A korong tengelye merőleges a fonálra, valamint a sebességre.     (Holics László)   Megoldás. a) Egyensúly (egyenesvonalú, egyenletes haladómozgás) esetén az összes erők forgatónyomatékának összege $0$ kell legyen. Ha nincs súrlódás, ez csak úgy teljesülhet, hogy induláskor, míg eléri az állandó sebességet a korong, a fonál egyenes, és meghosszabbítása illeszkedik a korong tengelyére (vagyis a tömegközéppontjára), tehát a fonál eddig vízszintes. Ettől kezdve azonban a kocsi akár csökkentheti is a sebességét, s a fonál meglazulva tetszőleges alakot vehet fel, a korong továbbra is egyenletesen halad. (Ilyen ideális eset azonban ténylegesen nem valósul meg, tehát a realitásnak csak a b) eset felel meg.) b) Ha van súrlódás, annak forgatónyomatékát kompenzálnia kell a fonálerő forgatónyomatékának (a nehézségi erőnek és a kényszererőnek nincs a tömegközéppontra nézve forgatónyomatéka). Írjuk fel az erők forgatónyomatékait a talajjal érintkező, az inerciarendszerben egyenletesen mozgó pontra! Erre nézve sem az $S$ súrlódási erőnek, sem a talaj által kifejtett kényszererőnek nincsen nyomatéka, így a fonálerő nyomatékának is zérusnak kell lennie. Ez csak úgy valósulhat meg, hogy a fonál meghosszabbítása átmegy a korongnak a talajjal érintkező pontján.     Az ábráról leolvasható, hogy a keresett hajlásszögre érvényes: $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{R}{2R+2R\text{sin}\alpha }\mathrm{.}}\end{array}$ Innen $\text{sin}\alpha$-ra vegyes másodfokú egyenletet kapunk: $\begin{array}{c}{\displaystyle 2\text{sin}{}^2\alpha +2\text{sin}\alpha -1=\mathrm{0,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{-2\pm \sqrt[]{4+8}}{4}=\frac{\sqrt[]{3}}{2}-\frac{1}{2}\mathrm{.}}\end{array}$ Innen a keresett hajlásszög: $\begin{array}{c}{\displaystyle \alpha =21\mathrm{,}{47}^{\circ }\mathrm{,}}\end{array}$ függetlenül a súrlódási együttható nagyságától. (Ez igen meglepő, ugyanis ha ily módon húzunk egy korongot akár ugrásszerűen változó súrlódású talajon, a fonálnak ,,meg sem szabad rezzenníe'', állandóan $21\mathrm{,}{47}^{\circ }$-ot kell bezárnia a vízszintessel. Ténylegesen elvégzett kísérletnél azonban a fonálban terjedő hatás sebességének véges volta miatt a korong berezegne, és nemegyensúlyi állapotain keresztül ,,föltornászná'' ‐ nem harmonikus ‐ rezgéseit.)   2. 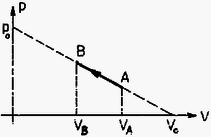Az ábra $p\left(V\right)$ grafikonon mutatja egy bizonyos mennyiségű oxigéngáz állapotváltozását.     Az ábrán szereplő $V_0$ térfogat és $p_0$ nyomás értékei: $V_0=12\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>d</mi><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>, <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>p</mi></mrow><mrow><mn>0</mn></mrow></msub></mrow></math>=1,2<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>10</mn></mrow><mrow><mn>5</mn></mrow></msup></mrow></math> }\text{Pa}$. A kezdeti (A) állapotban a gáz térfogata $V_A=\frac{2}{3}{V}_0$, hőmérséklete $T_A=300\text{K}$. A végső (B) állapotban $V_B=\frac{5}{12}{V}_0$. Határozza meg külön-külön, hogy mennyi hőt vesz fel, és mennyi hőt ad le a gáz a folyamatban! (Szegedi Ervin)   I. megoldás. Az ábráról látható, hogy fennáll $\begin{array}{c}{\displaystyle \frac{p_A}{V_0-V_A}=\frac{p_0}{V_0}\mathrm{,}\text{amiből}{p}_A=\frac{V_0-V_A}{V_0}{p}_0=\frac{1}{3}{p}_0=0\mathrm{,}4\cdot {10}^5\text{Pa, }}\end{array}$ hasonlóképpen $\begin{array}{c}{\displaystyle \frac{p_B}{V_0-V_B}=\frac{p_0}{V_0}\mathrm{,}\text{amiből}{p}_B=\frac{V_0-V_B}{V_0}{p}_0=\frac{7}{12}{p}_0=0\mathrm{,}7\cdot {10}^5\text{Pa. }}\end{array}$ A (B) állapotban a hőmérséklet: $\begin{array}{c}{\displaystyle \frac{p_A{V}_A}{T_A}=\frac{p_B{V}_B}{T_B}\mathrm{,}\text{amiből}{T}_B=\frac{p_B{V}_B}{p_A{V}_A}{T}_A=\frac{35}{32}{T}_A=328\mathrm{,}1\text{K. }}\end{array}$ Az $Nk$ szorzat a $p_A{V}_A=Nk{T}_A$ összefüggés alapján $\begin{array}{c}{\displaystyle Nk=\frac{p_A{V}_A}{T_A}=\frac{2}{9}\frac{p_0{V}_0}{T_A}=1\mathrm{,}067\frac{\text{J}}{\text{K}}\mathrm{.}}\end{array}$ (1) A folyamat $p\left(V\right)$ függvénye: $\begin{array}{c}{\displaystyle p\left(V\right)=p_0\left(1-\frac{V}{V_0}\right)\mathrm{.}}\end{array}$ (2) A folyamat $T\left(V\right)$ függvénye (1) és (2) felhasználásával: $\begin{array}{c}{\displaystyle T\left(V\right)=\frac{p\left(V\right)V}{Nk}=\frac{9}{2}{T}_A\left(1-\frac{V}{V_0}\right)V\mathrm{.}}\end{array}$ (3) Jelölje $Q\l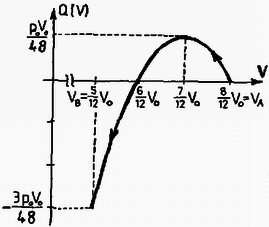eft(V\right)$ azt a hőt, amit a gáz a környezetétől felvesz, miközben térfogata $V_A$-ról $V$-re változik. Határozzuk meg a $Q\left(V\right)$ függvényt!   Az I. főtétel szerint: $\begin{array}{c}{\displaystyle \Delta E\left(V_A\to V\right)=Q\left(V\right)+W\left(V_A\to V\right)\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle Q\left(V\right)=\Delta E\left(V_A\to V\right)-W\left(V_A\to V\right)\mathrm{.}}\end{array}$ (4) Az energiaváltozás (1) és (2) felhasználásával: $\begin{array}{c}{\displaystyle \Delta E\left(V_A\to V\right)=\frac{5}{2}Nk\left(T-T_A\right)=p_0{V}_0\left[\frac{5}{2}\left(\frac{V}{V_0}\right)-\frac{5}{2}{\left(\frac{V}{V_0}\right)}^2-\frac{5}{9}\right]\mathrm{.}}\end{array}$ (5) A gázon végzett munka (2) felhasználásával: $\begin{array}{c}{\displaystyle W\left(V_A\to V\right)=\frac{p_A+p}{2}\left(V-V_A\right)=-p_0{V}_0\left[\left(\frac{V}{V_0}\right)-\frac{1}{2}{\left(\frac{V}{V_0}\right)}^2-\frac{4}{9}\right]\mathrm{.}}\end{array}$ (6) A $Q\left(V\right)$ függvény tehát (4), (5) és (6) alapján: $\begin{array}{c}{\displaystyle Q\left(V\right)=p_0{V}_0\left[-3{\left(\frac{V}{V_0}\right)}^2+\frac{7}{2}\left(\frac{V}{V_0}\right)-1\right]\mathrm{.}}\end{array}$ (7)     A $Q\left(V\right)$ függvény alapján megállapíthatók a következők. Miközben a gázt kezdeti $V_A$ térfogatáról fokozatosan összenyomjuk, a felvett hő növekszik, amíg a térfogat $7V_0/12$-re nem csökken. Eddig a gáz $\begin{array}{c}{\displaystyle Q_{\text{fel}}=Q\left(\frac{7}{12}{V}_0\right)=\frac{p_0{V}_0}{48}=30\text{<span style="font-weight: normal;font-style: normal;">J hőt vesz fel.</span>}}\end{array}$ A $7V_0/12$ térfogatról tovább összenyomva a gázt, hőt ad le. A leadott hő: $\begin{array}{c}{\displaystyle Q\left(V_B\right)=Q\left(\frac{7}{12}{V}_0\right)+Q\left(\frac{7}{12}{V}_0\to V_B\right)\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle -\frac{3p_0{V}_0}{48}=\frac{p_0{V}_0}{48}+Q\left(\frac{7}{12}{V}_0\to V_B\right)}\end{array}$ felhasználásával $\begin{array}{c}{\displaystyle Q\left(\frac{7}{12}{V}_0\to V_B\right)=-\frac{1}{12}{p}_0{V}_0=-120\text{J. }}\end{array}$ A folyamatban tehát a gáz $Q_{\text{le}}=120\text{J}$ hőt ad le.   II. megoldás. Azt, hogy mekkora térfogatig $\left(V_x\right)$ van hőfelvétel, más úton is megkaphatjuk. A gáz a $V_x$ térfogatig hőt vesz fel, de tovább összenyomva hőt ad le. Ez azt jelenti, hogy $V_x$ kis környezetében gyakorlatilag sem hőfelvétel, sem hőleadás nincs. Pontosabban fogalmazva: a folyamat $p\left(V\right)$ függvényét a $V_x$ pontban a gáz $\left[V_x\mathrm{,}p\left(V_x\right)\right]$ ponton átmenő adiabatája érinti. Egy tetszőleges $\left(V\mathrm{,}p\right)$ ponton átmenő adiabata meredekségére teljesül a következő: ${\displaystyle \begin{array}{c}\hfill {\displaystyle p=c\cdot V^{-\kappa }\left(c=\text{állandó}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{dp}{dV}=-\kappa {cV}^{-\kappa -1}=-\kappa \frac{c{V}^{-\kappa }}{V}\mathrm{,}}\hfill \end{array}}$ tehát $\begin{array}{c}{\displaystyle \frac{dp}{dV}=-\kappa \frac{p}{V}\mathrm{.}}\end{array}$ (8) A vizsgált folyamat $p\left(V\right)$ görbéje mentén $V$ térfogatnál az adiabata meredeksége (8) és (2) felhasználásával: $\begin{array}{c}{\displaystyle {\left(\frac{dp}{dV}\right)}_{\text{adiabata}}=-\kappa \frac{p_0}{V}\left(1-\frac{V}{V_0}\right)\mathrm{.}}\end{array}$ (9) A gáz $p\left(V\right)$ görbéjének meredeksége minden térfogatnál $-p_0/V_0$. A meredekségek egyenlőségéből (felhasználva, hogy oxigéngáz esetén $\kappa =7/5$): $\begin{array}{c}{\displaystyle -\frac{7}{5}\frac{p_0}{V_x}\left(1-\frac{V_x}{V_0}\right)=-\frac{p_0}{V_0}\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle V_x=\frac{7}{12}{V}_0\mathrm{.}}\end{array}$ A megoldás innen azonos az előzővel.   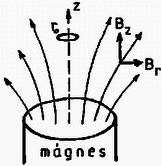3. Egy vékony, elhanyagolható ellenállású $\left(R=0\right)$ gyűrűt függőleges helyzetű, henger alakú rúdmágnes felett tartunk. A gyűrű tengelye egybeesik a mágnes tengelyével. A gyűrű körüli hengerszimmetrikus mágneses mező közelítőleg így jellemezhető a mágneses indukcióvektor függőleges és sugárirányú koordinátáival: $\begin{array}{c}{\displaystyle B_z=B_0\left(1-\alpha z\right)\text{és}{B}_r=B_0\beta r\mathrm{,}}\end{array}$ ahol $B_0\mathrm{,}\alpha \mathrm{,}\beta$ állandók, továbbá $z$ és $r$ függőleges, illetve sugárirányú helykoordináták.     Elengedés után a gyűrű lefelé kezd mozogni, miközben függőleges tengelyét megtartja. Az elengedés pillanatában a gyűrűben nem folyik áram. a) Vizsgáljuk meg, hogy mozgás közben a gyűrű belsejében időben állandó-e a mágneses fluxus! b) Milyen mozgást végez a gyűrű? Határozzuk meg a gyűrű függőleges koordinátájának időfüggését! c) Hogyan függ a gyűrűben folyó áram az időtől a mozgás során? Határozzuk meg az áram maximális értékét! (A gyűrű középpontjainak kezdeti koordinátái legyenek $z=0$ és $r=0$. A mozgás leírásakor hanyagoljuk el a légellenállást!) Adatok: $B_0=0\mathrm{,}01\text{T, <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>α</mi></math>=2<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>β</mi></math>=32 }\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math>}$, a gyűrű tömege $m=50\text{mg}$, a gyűrű önindukciós együtthatója $L=1\mathrm{,}3\cdot {10}^{-8}\text{H}$, a gyűrű sugara $r_0=0\mathrm{,}5\text{cm}$, a nehézségi gyorsulás $g=9\mathrm{,}8\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi><mo stretchy="false">/</mo><mi>s</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$. (Honyek Gyula)   Megoldás. a) A mágneses fluxusváltozás elektromotoros erőt indukál, ami áramot kelt: $\begin{array}{c}{\displaystyle \epsilon =\frac{\Delta \Phi }{\Delta t}=RI\mathrm{,}\text{ahol}\Phi =B_z\cdot r_0^2\pi +LI\mathrm{.}}\end{array}$ Mivel a körvezető ellenállása $R=0$, így az eredő elektromotoros erőnek is zérusnak kell lennie: $\epsilon =0$, vagyis a $\Phi$ mágneses fluxus állandó: $\begin{array}{c}{\displaystyle \Phi =B_0\left(1-\alpha z\right)r_0^2\pi +LI=\text{állandó}\mathrm{.}}\end{array}$ (1) A kezdeti feltételeket $\left(z=\mathrm{0,}I=0\right)$ figyelembe véve, az állandó értéke: $\begin{array}{c}{\displaystyle \Phi =B_0{r}_0^2\pi \mathrm{.}}\end{array}$ (2) b) Az (1) és (2) egyenletek alapján a kialakuló áram erőssége $\begin{array}{c}{\displaystyle I=\frac{1}{L}{B}_0\alpha r_0^2\pi z\mathrm{.}}\end{array}$ (3) Az áramjárta gyűrűre a külső mágneses mező erőt fejt ki: $\begin{array}{c}{\displaystyle F_z=-B_r\cdot I\left(z\right)\cdot 2r_0\pi =-B_0\beta r_0\cdot \frac{B_0\alpha r_0^2\pi }{L}\cdot 2r_0\pi \cdot z=-kz\mathrm{,}}\end{array}$ így a gyűrű mozgásegyenlete: $\begin{array}{c}{\displaystyle m{a}_z=F_z-mg=-kz-mg\mathrm{,}}\end{array}$ (4) ahol $\begin{array}{c}{\displaystyle k=\frac{2B_0^2\alpha \beta r_0^4{\pi }^2}{L}\mathrm{,}}\end{array}$ tehát a gyűrű harmonikus rezgőmozgást végez. A kezdeti feltételeket figyelembe véve a gyűrű mozgását a $\begin{array}{c}{\displaystyle z\left(t\right)=A\left(\text{cos}\omega t-1\right)}\end{array}$ (5) egyenlet írja le, ahol a körfrekvencia: $\begin{array}{c}{\displaystyle \omega =\sqrt[]{\frac{k}{m}}=\pi r_0^2{B}_0\sqrt[]{\frac{2\alpha \beta }{mL}}\mathrm{.}}\end{array}$ Az egyensúlyi helyzetet $\left(a_z=0\right)$, ill. az $A$ amplitúdót a (4) egyenlet alapján határozzuk meg: $\begin{array}{c}{\displaystyle z_0=-A=-\frac{mg}{k}=-\frac{mgL}{2B_0^2\alpha \beta r_0^4{\pi }^2}\mathrm{.}}\end{array}$ (6) Numerikusan: $\omega =31\mathrm{,}2\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>s</mi></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math>}$ és $A=1$ cm. c) Ha a (3) egyenletbe behelyettesítjük az (5) kifejezést, akkor megkapjuk az áram időfüggését: $\begin{array}{c}{\displaystyle I\left(t\right)=\frac{B_0\alpha r_0^2\pi }{L}\cdot A\left(\text{cos}\omega t-1\right)\mathrm{,}}\end{array}$ ill. az amplitúdó (6) kifejezését behelyettesítve: $\begin{array}{c}{\displaystyle I\left(t\right)=\frac{mg}{2\pi r_0^2{B}_0\beta }(\text{cos}\omega t-1)\mathrm{,}}\end{array}$ amiből az áram erősségének maximális értéke: $\begin{array}{c}{\displaystyle I_{\text{max}}=\frac{mg}{\pi r_0^2{B}_0\beta }\mathrm{.}}\end{array}$ Numerikusan: $I_{\text{max}}=39$ A. 1Mindegyik feladat megoldása a feladat kitűzőjétől származik.