Kezdőlap


Cím:	Olimpiai levelezési feladat megoldása
Szerző(k):	Veres Gábor
Füzet:	1992/október, 333 - 336. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A KöMaL 1991. évi 6. számában közültük az alábbi (pontversenyen kívüli) feladatot:
Négy azonos tömegű pontszerű testet azonos hosszúságú fonalak segítségével zárt, rombusz alakú láncba fűzünk, és a láncot egy $ω$ szögsebességgel forgó légpárnás asztalra helyezzük:
a) Hogyan fog mozogni a négy test, ha kezdetben a forgó asztalhoz képest nyugalomban voltak, a rendszer tömegközéppontja a forgástengelyen helyezkedett el, és a rombusz egyik szöge $α$ volt?
b) Hogyan mozog a rendszer, ha kezdetben a tömegközéppontja állt, és a forgó rendszerből nézve a két legközelebbi test egymás felé mozgott $v_{0}$ kezdősebességgel?
c) Írjuk le a rendszer legáltalánosabb mozgását mind az álló, mind pedig az $ω$ szögsebességgel forgó koordináta-rendszerből nézve!
(Feltételezhetjük, hogy a súrlódás elhanyagolható, és a fonalak mindvégig feszesek. A mozgást csak a testek összeütközéséig kell követnünk.)
Megoldás. Legyen a testek tömege egyenként $m$ , a fonalak hosszúsága $l$ , a testeket jelöljük $A, B, C és D$ betűkkel, tegyük fel továbbá, hogy az asztal vízszintes és $0^{\circ} < α < 180^{\circ}$ .
a) A testekre ható gravitációs erő és az asztal tartóereje kiegyenlítik egymást, ezért mondhatjuk azt, hogy a testekre csak a fonálerők hatnak. A szimmetria miatt az $F$ fonálerők egyenlőek, ezért egy kiszemelt testre ható fonálerők eredője mindig az $O$ tömegközéppont felé mutat. Az eredő erő nagysága az $A$ és $C$ testek esetében: $F_{1} = 2 F cos (α / 2)$ ; a $B$ és a $D$ test esetében: $F_{2} = 2 F s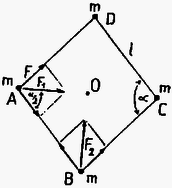in (α / 2)$ (1. ábra).

1. ábra

A kezdő pillanatban a testek sebessége a forgó rendszerben zérus, így nem lép fel a Coriolis-erő. Tegyük fel, hogy

2 F cos \frac{α}{2} = F_{1} > m (l \cdot cos \frac{α}{2}) ω^{2} .

Ekkor az

A

és

C

testek az

O

tömegközéppont felé kezdenek gyorsulni, a másik két test ‐ a fonalak feszességéből adódóan ‐ nyílván a

\vec{B O}

, ill. a

\vec{D O}

vektorokkal ellentétes irányban fog gyorsulni, aminek feltétele, hogy

F_{2} = 2 F sin \frac{α}{2} < m (l \cdot sin \frac{α}{2}) ω^{2}

legyen. A két egyenlőtlenségből a következő ellentmondásra jutunk:

\frac{1}{2} m l ω^{2} < F < \frac{1}{2} m l ω^{2}

; ezért feltételezésünk rossz volt. Hasonlóan juthatunk ellentmondásra akkor is, ha feltételezzük, hogy

2 F cos \frac{α}{2} = F_{1} < m (l \cdot cos \frac{α}{2}) ω^{2}

, ezért csak a következő eset valósulhat meg:

F_{1} = m (l \cdot cos \frac{α}{2}) ω^{2}

és

F_{2} = m (l \cdot sin \frac{α}{2}) ω^{2}

. A testek gyorsulása a forgó rendszerből nézve zérus; a testek tehát mindvégig mozdulatlanok maradnak. Példaként: az

A

test helykoordinátái az

ω

szögsebességgel forgó koordináta-rendszerben:

x_{A} (t) = - l cos (α / 2); y_{A} (t) = 0

. Az álló koordináta-rendszerből (inerciarendszerből) nézve mindegyik test egyenletes körmozgást végez

ω

szögsebességgel az

O

tömegközéppont körül. Példaként az

A

test helykoordinátái:

\begin{matrix} x_{A} (t) = l cos \frac{α}{2} \cdot cos (ω t + π); y_{A} (t) = l cos \frac{α}{2} \cdot sin (ω t + π) . \end{matrix}

b) Legyen

α

a rombusz kisebbik szöge; tehát

0^{\circ} < α \leq 90^{\circ}

. A feladat szövege szerint a fonalak mindvégig feszesek maradnak. Az

O

tömegközéppont ‐ a rombusz egymásra merőleges átlóinak metszéspontja és egyben forgástengely ‐ a mozgás során nem mozdul el. Képzeljük el a mozgást úgy, hogy a fonállal összekötött testek két egymásra merőleges, elhanyagolható tömegű, mereven összeerősített rúdra vannak felfűzve, és rajtuk súrlódásmentesen csúszhatnak, rájuk merőlegesen erőt fejthetnek ki. A fonalak mindig feszesek és rombuszt alkotnak, ezért ezekkel a rudakkal kiegészítve a rendszer pontosan úgy fog mozogni, mint ahogy nélkülük mozogna. Tegyük fel, hogy a mozgás egy pillanatában a rudazat a testekkel együtt valamilyen

ω'

szögsebességgel forog az álló koordináta-rendszerhez képest, a rudakhoz képest a feszes fonalak

(\pm) ω''

szögsebességgel forognak és

φ

, illetve

90^{\circ} - φ

szöget zárnak be a rudakkal. (A 2. ábrán egy kiszemelt fonál látható.)

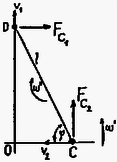2. ábra

Természetesen a fonalak nemcsak forgó, hanem haladó mozgást is végeznek az

ω'

szögsebességgel forgó ‐ rudakhoz rögzített ‐ koordináta-rendszerben. Amint látni fogjuk, a megoldás szempontjából célszerű ezzel az

ω''

szögsebességgel kifejezni a testek sebességét. Így a

D

test sebessége:

v_{1} = l ω'' cos φ,

ugyanis ha a

C

testet rögzítenénk, akkor az

ω''

pillanatnyi szögsebességű körmozgást végző

D

test sebességének

O D

irányú vetülete

l ω'' cos φ

lenne. (S mivel a

C

pont mozgása

O D

-re merőleges, a

D

pont sebessége nem rögzített

C

esetén is

v_{1}

kell legyen.) Hasonlóan a

C

test sebessége:

v_{2} = l ω'' sin φ .

Vajon állandó-e időben az

ω'

szögsebesség? A sugár irányban

v

sebességgel mozgó testek egy

ω

szögsebességgel forgó koordináta-rendszerben

F_{C} = 2 m v ω

tehetetlenségi erőt fejtenek ki, ez a Coriolis-erő. Nézzük meg, van-e ezeknek az erőknek forgatónyomatéka

O

pontra nézve! A

C

és

D

testek sugárirányú sebességéből származó

F_{C_{1}}

és

F_{C_{2}}

Coriolis-erők okozta, rudazatra ható forgatónyomatékok összege:

\begin{matrix} \sum M = M_{1} + M_{2} = F_{C_{1}} \cdot l sin φ - F_{C_{2}} \cdot l cos φ = 2 m ω' v_{1} \cdot l sin φ - 2 m ω' v_{2} \cdot l cos φ = \end{matrix}

\begin{matrix} = 2 m l ω' (l ω'' sin φ \cdot l cos φ - l ω'' sin φ \cdot l cos φ) = 0. \end{matrix}

A

és

B

testekre ható Coriolis-erők okozta forgatónyomatékok is kiejtik egymást, tehát a rudakra ható eredő forgatónyomaték

ω'

-től és

ω''

-től (vagyis a testek sebességétől) függetlenül zérus. Ez azt jelenti, hogy a rudazat kezdeti

ω

szögsebessége a mozgás során nem változik meg, állandó marad:

ω' \equiv ω

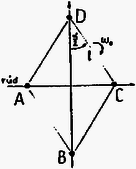3. ábra

A fent említett

(ω'')

"fonálszögsebesség'' kezdetben

ω_{0}

volt (3.ábra):

v_{0} = l ω_{0} sin \frac{α}{2}

-ből kapjuk:

ω_{0} = \frac{v_{0}}{l \cdot sin (α / 2)}

. Tegyük fel, hogy a mozgás egy pillanatában a fonalak szögsebességének nagysága

ω''

és a rombusz egyik szöge

φ

. Ekkor a rendszer összes mozgásienergiája (a zárójelben a kétféle forgásból származó sebességek négyzetei találhatók):

\begin{matrix} E_{összes} = 2 \cdot \frac{1}{2} m (l^{2} cos^{2} \frac{φ}{2} \cdot ω^{2} + l^{2} sin^{2} \frac{φ}{2} \cdot ω^{2} + l^{2} ω''^{2} \cdot cos^{2} \frac{φ}{2} + l^{2} ω''^{2} \cdot sin^{2} \frac{φ}{2}) = \\ = m l^{2} \cdot (ω^{2} + ω''^{2}) . \end{matrix}

Mivel mind az összenergia, mind

ω

állandó, ezért a fonalak

ω''

szögsebessége is állandó (!), nagysága pedig:

ω'' = ω_{0} = \frac{v_{0}}{l \cdot sin (α / 2)}

.
Ezek után már könnyen felírhatók a testek helykoordinátái az idő függvényében. Szemeljük ki például a

C

testet! Összeütközésig a rombusz félszöge az

\begin{matrix} \frac{α'}{2} (t) = \frac{α}{2} + ω_{0} t = \frac{v_{0}}{l \cdot sin (α / 2)} t + \frac{α}{2} \end{matrix}

képlet szerint, a

C

test egyik koordinátája az

ω

szögsebességgel forgó

(x', y')

koordináta-rendszerben

\begin{matrix} x'_{C} (t) = l \cdot sin [\frac{α'}{2} (t)] = l \cdot sin (\frac{v_{0} t}{l \cdot sin (α / 2)} + \frac{α}{2}) \end{matrix}

képlet szerint változik, vagyis a test harmonikus rezgőmozgást végez

(y'_{C} (t) = 0)

. (Ez hasonlóan megmutatható a többi testnél is.) Érdekes, hogy a rezgőmozgás

ω_{0}

körfrekvenciája a

v_{0}

kezdeti sebességtől függ, tehát változtatni lehet az értékét.

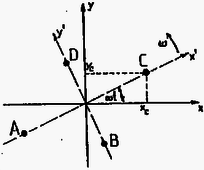4. ábra

Az álló

(x

y)

koordináta-rendszerből nézve a testek egy

ω

szögsebességű egyenletes körmozgásból és egy harmonikus rezgőmozgásból összetett mozgást végeznek. A

C

test helykoordinátái tehát (4. ábra):

\begin{matrix} x_{C} (t) = x'_{C} (t) \cdot cos (ω t) = l \cdot sin (\frac{v_{0} t}{l \cdot sin (α / 2)} + \frac{α}{2}) \cdot cos (ω t); \\ y_{C} (t) = x'_{C} (t) \cdot sin (ω t) = l \cdot sin (\frac{v_{0} t}{l \cdot sin (α / 2)} + \frac{α}{2}) \cdot sin (ω t) . \end{matrix}

A többi testnél is hasonlóan írhatók fel a helykoordináták.
Az egymáshoz közeledő testek idővel összeütköznek. Ha az ütközést igen gyorsnak és tökéletesen rugalmasnak tételezzük fel, akkor a fenti képletek kis változtatással érvényesek maradnak a mozgás egészére ‐ az ütközés(ek) után is:

\begin{matrix} x_{C} (t) = l \cdot cos (ω t) \cdot | sin (\frac{v_{0} t}{l \cdot sin (\frac{α}{2})} + \frac{α}{2}) |; \end{matrix}

Egy kiszemelt test néhány lehetséges pályájának számítógéppel készített rajzát az 5‐7. ábrák mutatják.

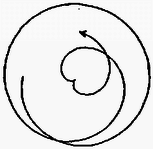5. ábra

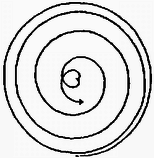6. ábra

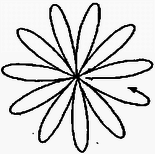7. ábra

Veres Gábor (Balassagyarmat, Balassi B. Gimn., III. o. t.)