Kezdőlap


Cím:	1991. Beszámoló a fizika OKTV-ről
Szerző(k):	Holics László
Füzet:	1992/május, 225 - 232. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A verseny három kategóriában folyt le. Az I. kategóriában a szakközépiskolai tanulók versenyeztek. A II. kategóriába tartozott minden III. osztályos tanuló (kivéve a speciális fizika és komplex természettudományi tantervű osztályokat), továbbá azok a IV. osztályos tanulók, akik fizikából nem vettek részt fakultáción. A III. kategóriába tartoztak a fizikából fakultáción részt vevő IV. osztályos tanulók, valamint a speciális és komplex tantervű III. és IV osztályos tanulók. A II. és III. kategóriában a feladatok ugyanazok voltak.
A verseny első fordulóját 1991. január 8-án, második fordulóját március 5-én, a harmadikat április 23-án rendezték meg.
Az idei versenyen résztvevők számának megoszlását az alábbi táblázat mutatja:

\begin{matrix} Az OKTV-n résztvevők száma \\ Indultak & Első fordulóból belküldve & Másodikra behíva \\ I. kat. 1849 & 309 & 120 \\ II. kat. 2619 & 168 & 142 \\ III. kat. 1601 & 115 & 115 \end{matrix}

A versenyen az I. kategóriában 5, a II. és III. kategóriában 10 ‐ 10 versenyző ért el helyezést, további 15, ill. 22 és 21 kapott dicséretet.
Az iskolai válogató forduló után behívott versenyzőknek a következő feladatsort kellett megoldaniuk:
I. kategória
1. Egy vékonyfalú, légritkított térben lévő üvegcső egyik vége zárt, másik végére folyadékhártya feszül. A hengeren belül és kívül

p_{o}

nyomású,

T_{o}

hőmérsékletű levegő van. Az üvegcső hossza

h

, sugara

R

. A folyadék felületi feszültsége

α

. A hőmérséklet lassan emelkedni kezd.
a) Mekkora hőmérsékletnél legnagyobb a bezárt levegő nyomása?
b) Mennyi hőt vesz fel az elzárt levegő a maximális nyomású állapot eléréséig?

R = 5 mm, h = 25 mm, T_{o} = 250 K, p_{o} = 1000 Pa, α = 5 \cdot 10^{- 2} {J/m}^{2}

.
Tegyük fel, hogy a vizsgált nyomás- és hőmérséklet-tartományban a folyadék távol van a forrástól.
(Szegedi Ervin)

Megoldás. A melegedés kezdete után az emelkedő hőmérséklet miatt a hártya egyre inkább kidudorodik, az

r

-rel jelölt görbületi sugár egyre csökken.

Mivel a gáz nyomása a külső nyomással és a hártya görbületi nyomásával tart egyensúlyt:

\begin{matrix} p = p_{0} + \frac{4 α}{r} . \end{matrix}

Látható, hogy ebben a szakaszban a nyomás növekszik. Az ábrából látszik, hogy

r

legkisebb értéke

R

lehet. Amikor ez bekövetkezik, a hártya pontosan félgömb alakú. A nyomásmaximum

\begin{matrix} p_{m a x} = p_{o} + \frac{4 α}{R} = 1040 Pa . \end{matrix}

(Ugyanerre az eredményre juthatunk a görbületi nyomás fogalmának felhasználása nélkül is. Jelölje

F

a cső által a hártyára kifejtett eredő erőt! Az ábra szerint az a) és a c) helyzetben

F < 4 R π α,

mivel

F

az elemi erők szimmetriatengely-irányú komponenseinek összege. A b) esetben

F = 4 R π α,

ekkor

F

maximális. A hártya egyensúlya miatt
a.)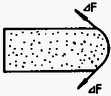

\begin{matrix} p R^{2} π = F + p_{o} R^{2} π, \end{matrix}

amiből

\begin{matrix} p = p_{o} + \frac{F}{R^{2} π} . \end{matrix}

Felhasználva

F

maximális értékét

p_{m a x}

-ra a fenti eredményt kapjuk.)
A kérdezett hőmérséklet a gáztörvény alapján számítható:

\begin{matrix} \frac{p_{o} R^{2} π h}{T_{o}} = \frac{p_{m a x} [R^{2} π h + (2 / 3) R^{3} π]}{T}, \end{matrix}

ahonnan

\begin{matrix} T = \frac{p_{m a x} [h + (2 / 3) R]}{p_{o} h} T_{o} = 295 K . \end{matrix}

b) Az első főtétel szerint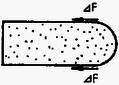

Q = Δ E + W_{g}

Az energiaváltozás könnyen számolható:

\begin{matrix} Δ E = \frac{f}{2} N k Δ T = \frac{f}{2} \frac{p_{o} R^{2} π h}{T_{o}} Δ T = 8,8 \cdot 10^{- 4} J . \end{matrix}

A gáz munkája egyrészt megnöveli a hártya energiáját, másrészt megemeli a külső levegőt.

\begin{matrix} W_{g} = 2 α (2 R^{2} π - R^{2} π) + p_{o} \frac{2}{3} R^{3} π = 2,7 \cdot 10^{- 4} J . \end{matrix}

Az első főtétel alapján:

\b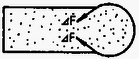egin{matrix} Q = 11,5 \cdot 10^{- 4} J . \end{matrix}

c.)

2. Egy fémhenger

ω

szögsebességgel forog szimmetriatengelye körül.

A

henger tengelyirányú,

B

indukciójú homogén mágneses mezőben van.
a) Határozza meg a töltéssűrűséget a henger belsejében!
b) Milyen szögsebességnél lesz zérus a töltéssűrűség?
(Szegedi Ervin)

Megoldás. A fémhenger forgási iránya szerint két esetet kell megkülönböztetnünk: ha

B

és

w

egyező, illetve ha ellentétes irányú.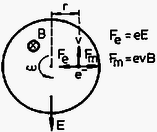

B

és

ω

ellentétes irányú:
Azt az esetet vizsgáljuk, amikor a fém vezetési (szabad) elektronjai már nem végeznek rendezett mozgást a hengerhez képest. Az ábrán egy kiválasztott elektronra ható (lényeges) erőket tüntettük fel: a mágneses Lorentz-erőt és a szétválasztott töltések mezejéből származó elektromos erőt. A Lorentz-erő most sugárirányban kifelé mutat.
Az elektron a körpálya középpontja felé gyorsul, következésképpen az elektromos erőnek a körpálya közepe felé kell hatnia. Ez azt jelenti, hogy az elektromos térerősség radiálisan kifelé mutat.
Az elektron mozgásegyenlete a vektorok abszolút értékeivel felírva:

\begin{matrix} E e - e r ω B = m r ω^{2}, \end{matrix}

(1 )

ahonnan az elektromos térerősség nagysága:

\begin{matrix} E = \frac{e ω B + m ω^{2}}{e} r . \end{matrix}

(2)

Milyen töltéseloszlás kelti a (2) szerinti elektromos térerősséget? Ismeretes, hogy egy térfogatában homogén módon töltött hosszú henger belsejében a térerősség nagysága:

\begin{matrix} E = \frac{ϱ}{2 ε_{o}} r, \end{matrix}

(3)

és pozitív töltéssűrűség esetén radiálisan kifelé mutat, vagyis ugyanolyan szerkezetű, mint a forgó hengerben kialakuló elektromos mező (azzal a figyelemre méltó különbséggel, hogy a forgó fémben még rövid henger esetében is egzakt eredményt kapunk, ui. a merev forgás stacionárius állapotához tartozó erőeloszlást csak ilyen töltés-eloszlás tudja biztosítani). Ezt felhasználva arra kell következtetnünk, hogy a forgó henger belsejében a töltéssűrűség konstans. (2) és (3) alapján e töltéssűrűség nagysága:

\begin{matrix} ϱ = \frac{2 ε_{o} ω (e B + m ω)}{e} . \end{matrix}

(4)

Az összességében semleges henger belseje pozitív töltésű, a megfelelő negatív töltés a henger külső szélén helyezkedik el.

B) Ha

B

és

ω

azonos irányú:
Ebben az esetben a mágneses Lorentz-erő a kör közepe felé mutat. Három aleset lehetséges:
(a)

\begin{matrix} m r ω^{2} < e r ω B \to ω < e B / m . \end{matrix}

Ekkor az elektromos erő kifelé,

E

a henger tengelye felé mutat.
(b)

\begin{matrix} m r ω^{2} = e r ω B \to ω = e B / m . \end{matrix}

(5)

Ekkor a Lorentz-erő körpályán tartja az elektronokat, nincs elektromos mező, a töltéssűrűség zérus. Ez felel meg a feladat

b

) kérdésére keresett megoldásnak!
(c)

\begin{matrix} m r ω^{2} > e r ω B \to ω > e B / m . \end{matrix}

Ekkor az elektromos erő a kör közepe felé, az

E

elektromos térerősség sugárirányban kifelé mutat.
A mozgásegyenletek:

\begin{matrix} (a) eset & (c) eset \\ m r ω^{2} & = e r ω B - e E, & m r ω^{2} & = e r ω B + e E, \\ E & = \frac{e ω B - m ω^{2}}{e} r, & E & = \frac{m ω^{2} - e ω B}{e} r, & (6) \\ ϱ & = \frac{2 ε_{0} ω (e B - m ω)}{e} . & ϱ & = \frac{2 ε_{0} ω (m ω - e B)}{e} . & (7) \end{matrix}

Az (a) esetben belül negatív, a (c) esetben belül pozitív töltéssűrűség van.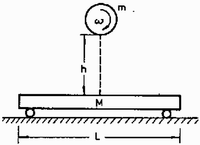

3. Egy

m = 80 kg

tömegű,

R = 0,2 m

sugarú merev tömör gömböt vízszintes szimmetriatengelye körül

ω

szögsebességgel megpörgetünk, majd kezdősebesség nélkül

h = 1, 25 m

magasból egy

M = 200 kg

tömegű, kezdetben nyugvó, könnyen gördülő kiskocsinak pontosan a közepére ejtjük. (A kocsi hossztengelye a forgás síkjára illeszkedik.) A kocsi ütközéskor fellépő deformációja abszolút rugalmas, az ütközés pillanatszerű. A gömb az ütközés teljes ideje alatt csúszik A csúszási súrlódási együttható a gömb és a kocsi között

μ = 0, 1

. A gömb a kocsiról visszapattanva ismét a kocsira esik.

a) Legalább milyen hosszú a kocsi?
b) Legalább mekkora volt a gömb kezdeti szögsebessége?
c) Mekkora a mechanikai energiaveszteség az első és a második ütközés alatt, ha a gömböt a b) kérdés szerinti minimális szögsebességgel indítottuk?
d) Mekkora a súrlódási erők összes munkája, mekkora munkát végzett a gömb a kocsin és a kocsi a gömbön?
e) Mennyivel nőtt az egyes testek haladómozgási energiája? Hogyan változott a forgási energia?
(Holics László)

Megoldás. a) A gömb leérkezésének sebessége

v_{1} = \sqrt[]{2 g h} = 5 m/s.

Az ütközéskor fellépő lendületváltozás

y

komponensének nagysága:

Δ I_{y} = 2 m v_{y} = 2 \sqrt[]{2 g h} = 800 Ns

, a vízszintes komponenséé pedig

Δ I_{x} = S Δ t,

ahol

S

az átlagos súrlódási erő.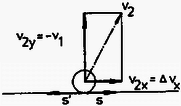

Az ezalatt ható átlagos kényszererő:

\begin{matrix} K = \frac{Δ I_{y}}{▵ t} = \frac{2 m \sqrt[]{2 g h}}{Δ t} . \end{matrix}

Ezzel a vízszintes lendület:

\begin{matrix} I_{x} = Δ I_{x} = S Δ t = μ K Δ t = μ \frac{2 m \sqrt[]{2 g h}}{Δ t} Δ t = 2 μ m \sqrt[]{2 g h} = 80 Ns . \end{matrix}

A külső erők mind függőlegesek, tehát a rendszer vízszintes lendületváltozása

0

, vagyis

M V = m v_{2 x}

, ahol

\begin{matrix} v_{2 x} = \frac{Δ I_{x}}{m} = 2 μ v_{1} = 2 μ \sqrt[]{2 g h} = 1 m/s \end{matrix}

és

\begin{matrix} V = \frac{m}{M} v_{2 x} = 2 \frac{m}{M} μ v_{1} = 2 μ \frac{m}{M} \sqrt[]{2 g h} = 0,4 m/s. \end{matrix}

Az abszolút rugalmas deformáció miatt a gömb visszapattan és ugyanolyan magasra repül, mint ahonnan leesett. Ezért a visszapattanás függőleges sebességkomponensének nagysága megegyezik a leérkezés

v_{1}

sebességével. Az ütközés után ferde hajítás jön létre, s a két ütközés között eltelt idő, vagyis a hajítás ideje:

\begin{matrix} t = 2 v_{1} / g = \sqrt[]{8 h / g} = 1 s . \end{matrix}

Ezalatt a gömb a földhöz képest

Δ x = v_{2 x} t = 2 μ \sqrt[]{16 h^{2}} = 8 μ h = 1 m

utat tesz meg jobbra, míg a kocsi

\begin{matrix} Δ X = V t = \frac{m}{M} Δ x = \frac{80}{200} \cdot 1 m = 0, 4 m \end{matrix}

nagyságú utat tesz meg balra. A két ütközés helye közötti távolság: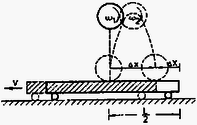

d = Δ X + Δ x = 1, 4 m .

A kocsi hossza tehát legalább:

\begin{matrix} L = 2 d = 16 μ h \frac{m + M}{M} = 2, 8 m. \end{matrix}

b) A gömb csúszó főkörének kerületi sebessége, ha a forgás éppen a tapadásig lassul:

v_{rel} = V + v_{2 x}

. A visszapattanás utáni szögsebesség minimális értéke (vagyis ha éppen a tiszta gördülésig csökken):

\begin{matrix} ω_{2} = \frac{v_{rel}}{R} = \frac{V + v_{2 x}}{R} = 4 μ \frac{m + M}{R M} \sqrt[]{g h} = 7 s^{- 1}, \end{matrix}

ahol

v_{rel}

a kerület alsó pontjának a kocsihoz viszonyított sebessége.
A csúszási súrlódási erő fékező forgatónyomatékának átlagos értéke:

M = S R,

ahol

S = μ K = μ \frac{2 m \sqrt[]{2 g h}}{Δ t},

és ezzel a forgatónyomaték-tétel szerint:

\begin{matrix} M = μ \frac{2 m \sqrt[]{2 g h}}{Δ t} R = - \frac{Θ Δ ω}{Δ t} . \end{matrix}

Δ t

kiesik, tehát:

\begin{matrix} | Δ ω | = ω_{1} - ω_{2} = μ \frac{2 m \sqrt[]{2 g h}}{\frac{2}{3} m R^{2}} R = \frac{5 μ \sqrt[]{2 g h}}{R} = 12, 5 s^{- 1}, \end{matrix}

így az induláskori szögsebesség keresett legkisebb értéke:

\begin{matrix} ω_{1_{min}} = ω_{2} + | Δ ω | = 7 s^{- 1} + 12, 5 s^{- 1} = 19, 5 s^{- 1} . \end{matrix}

c) Ha a második ütközés alatt már végig tapad a gömb, csak az első ütközés közben van mechanikai energiadisszipáció. Az ütközés közben az

y

irányú ,,szabadsági fokra'' jutó mozgási energia a rugalmas erő miatt nem változik, az

x

irányra jutó transzlációs energia a súrlódási erő hatására megnő (úgy a golyóé, mind a kocsié), a forgásra jutó energia viszont lecsökken. Határozzuk meg a mechanikai energiaveszteséget! (Ez éppen az összes súrlódási munkával egyenlő.)
A munkatétel szerint

\sum W = Δ E_{kin}

, vagyis:

\begin{matrix} Δ E_{mech} = \sum W = W_{m \to M} + W_{M \to m} = \frac{1}{2} M V^{2} + \frac{1}{2} m v_{x}^{2} + \frac{1}{2} Θ (ω_{2}^{2} - ω_{1}^{2}), \end{matrix}

ahol az első tag a kocsi, a második tag a golyó haladó mozgásának energianövekedése, a harmadik tag a forgási energia csökkenése.
A kapott kifejezések behelyettesítése és a műveletek elvégzése után:

\begin{matrix} Δ E_{mech} = - \frac{m (4 m + 14 M)}{M} μ^{2} g h = - 156 J . \end{matrix}

d) A súrlódási erő összes munkáját a c)-re adott válaszban már megkaptuk. A gömbnek a kocsin végzett munkája:

\begin{matrix} W_{g \to k} = \frac{1}{2} M V^{2} = 4 \frac{m^{2}}{M} μ^{2} g h = + 16 J, \end{matrix}

míg a kocsi a gömbön:

\begin{matrix} W_{k \to g} = \sum W - W_{g \to k} = - 2 \frac{(4 m + 7 M) m}{M} μ^{2} g h = - 172 J \end{matrix}

munkát végez. (Mivel a gömb transzlációs kinetikus energiája megnő, a forgási energiának kell csökkennie.)
e) A kocsi mozgási energiája

Δ E_{M} = W_{g \to k} = + 16 J

értékkel nőtt, a gömb haladó mozgási energiája

Δ E_{m_{transz}} = \frac{1}{2} m v_{2 x}^{2} = μ m \sqrt[]{2 g h} = + 40 J

értékkel nőtt az ütközés alatt. Végül a gömb forgási energiája

\begin{matrix} Δ E_{m_{rot}} = \frac{1}{2} Θ (ω_{2}^{2} - ω_{1}^{2}) = - 2 m g h \frac{4 m + 9 M}{M} μ^{2} = - 212 J \end{matrix}

értékkel változott, tehát valóban csökkent.

Energiamérleg: Eredeti összes mechanikai energia:

m g h + \frac{1}{2} Θ ω_{1}^{2} = 1000 J + 243, 36 J = 1243, 36 J .

A mechanikai energia az ütközés után:

\frac{1}{2} M V^{2} + \frac{1}{2} m v_{2}^{2} + \frac{1}{2} Θ ω_{2}^{2} = 16 J + 40 J + 31, 36 J = 1087, 36 J .

A különbség:

Δ E_{mech} = - 156 J .

A forgási energia csökkenése:

Δ E_{rot} = \frac{1}{2} Θ (ω_{2}^{2} - ω_{1}^{2}) = - 212 J .

Az összes súrlódási munka, vagyis a rendszer mozgási energiájának (jelen esetben a teljes mechanikai energiájának) megváltozása

- 156 J,

ami a következőképpen oszlik meg:

\to - 212 J

forgási energiaváltozás,

- 156 J

\to + 56 J

haladási energiaváltozás.

243, 36 J

eredeti forgási energiából

156 J

disszipálódott és

56 J

ment át transzlációs kinetikus energiába, maradt

31, 36 J

forgási energia.

II. és III. kategória
A gimnáziumi tanulók és a szakközépiskolások első két feladata megegyezett. A harmadik feladat a következő volt:

3. Kezdetben egyik lapjával vízszintes, sima síkon nyugvó,

m = 8 kg

tömegű tömör,

l = 20 cm

élhosszúságú kocka egyik alsó élének középpontjához l hosszúságú fonál egyik végét erősítettük. Mekkora állandó erőt fejt ki a kocka a talajra és mekkora erőt fejt ki a fonál a kockára, ha a fonál másik végét a síkhoz szorítva

a = 3 g

gyorsulással húzzuk úgy, hogy a fonál mindig merőleges maradjon a hozzá csatlakozó élre?
(Holics László)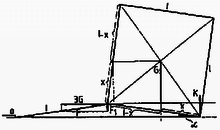

Megoldás. Az ábra alapján annak jelöléseivel felírhatjuk a kocka mozgásegyenletét függőleges és vízszintes irányokra:

\begin{matrix} K - F_{1} - G = 0, & (1) \\ F_{1} ctgα=3G, & (2) \\ K x cos α + F_{1} (l - x) cos α = 3 G x cos α . & (3) \end{matrix}

Fennáll továbbá

\begin{matrix} \frac{l}{2} - x = \frac{l}{2} tgα. \end{matrix}

(4)

(2)-és (4)ből

\begin{matrix} F_{1} = 3 G (l - \frac{2 x}{l}), \end{matrix}

(5)

(1)-és (3)-ból

\begin{matrix} (F_{1} + G) x + F_{1} (l - x) - 3 G x = 0, \end{matrix}

(6)

végül (5) és (6) alapján a fonálerő függőleges komponensének nagysága

\begin{matrix} F_{1} = \frac{3}{4} G . \end{matrix}

A talajt nyomó erő:

\begin{matrix} K = F_{1} + G = \frac{7}{4} m g = 140 N . \end{matrix}

Ennek segítségével a keresett fonálerő:

\begin{matrix} F = \sqrt[]{F_{1}^{2} + {(3 G)}^{2}} = \sqrt[]{\frac{9}{16} G^{2} + 9 G^{2}} = \frac{3}{4} \sqrt[]{17} G = 247, 4 N . \end{matrix}

A kocka alaplapja

α = arctg\frac{F_{1}}{3 G}= arctg\frac{1}{4}=14^{\circ}

-kal emelkedik meg.

A verseny elbírálása a 2. és a 3. fordulón mutatott teljesítmények alapján történt.

A fizika I. kategória eredményei:

I. díj: Liptay Pál (Salgótarján, Stromfeld Aurél Műszaki Szki., IV. o. t., tanára: Kovács F. Gáborné),
II. díj: Váczi Pál (Paks, Atomerőmű Vállalat Energetikai Szki., IV. o. t., tanárai: Torma Béla, Straubingerné Kemler Anikó),
III. díj: Gócs Viktor (Debrecen, Híradásipari Műszaki Szki, IV. o. t., tanára: dr. Kopcsa József),
4. Török Imre (Debrecen, Híradásipari Műszaki Szki., IV. o. t., tanára: dr. Kopcsa József),
5. Jakó Attila (Budapest, Latinca Sándor Szki., IV. o. t., tanára: Pataki Anikó).

További helyezettek:
6. Bonifert Csaba (Vác, Ipari Szki, IV. o. t.), 7. Szedő Gábor (Budapest, Egressy Gábor Ipari Szki., IV. o. t), 8. Bleuer Csaba (Budapest, Egressy Gábor Ipari Szki, IV o. t.), 9. Fejér Gábor (Pécs, Pollack Mihály Építőipari Szki., IV. o. t.), 10. Kósa István (Nyíregyháza, Vásárhelyi Pál Szki., IV. o. t.), 11. Gyivicsán Zoltán (Kaposvár, Ipari Szki., III. o. t.), 12. Majoros László (Budapest, Egressy Gábor Ipari Szki., IV. o. t.), 13. Gyuró János (Hajdúnánás, Kőrösi Csoma Sándor Gimn. és Szki., III. o. t.), 14. Lugosi László (Pécs, Zipernowszki Károly Műszaki Szki., IV. o. t.), 15. Ligárt László (Győr, Jedlik Ányos Szki., III. o. t.), 16. Blau Róbert (Budapest, Puskás Tivadar Szki., III. o. t.), 17. Zsók András (Paks, Atomerőmű Energetikai Szakképzési Intézet III. o. t), 18. Dénes Tamás (Pécs, Zipernowszky Károly Ipari Szki., IV. o. t.), 19. Rohály Péter (Miskolc, Bláthy Ottó Szki., III. o. t.), 20. Tóth Gábor (Budapest, Landler Jenő Szki., IV. o. t.), 21. Solymári György (Budapest, Egressy Gábor Szki., IV o. t.).

A fizika II. kategória eredményei:

I. díj: Káli Szabolcs (Budapest, Fazekas Mihály Gimn., IV o. t., tanára: Horváth Gábor),
II. díj: Daruka István (Karcag, Gábor Áron Gimn., IV. o. t., tanára: Olajos István),
III. díj: Boncz András (Zalaegerszeg, Zrínyi Miklós Gimn., IV o. t., tanára: Pálovics Róbert),
4. Sarang Attila (Eger, Csiky Gergely Gimn., III. o.t., tanára: Hevesi László),
5. Fedorcsák Péter (Miskolc, Földes Ferenc Gimn., IV. o. t., tanárai: Zsúdel Ferenc és Dolák Gabriella),
6. Falus Péter (Budapest, Trefort Ágoston Gimn., IV. o. t., tanára: Honyek Gyula),
7. Szendrői Balázs (Budapest, Fazekas Mihály Gimn., III. o. t., tanára: Horváth Gábor),
8. Gróf Attila (Budapest, Fazekas Mihály Gimn., IV o. t., tanára: Horváth Gábor),
9. Török János (Zalaegerszeg, Zrínyi Miklós Gimn., IV. o. t., tanára: Pálovics Róbert),
10. Szűts Dávid (Budapest, Fazekas Mihály Gimn., III. o. t., tanára: Horváth Gábor).

További helyezettek:
11. Kiss István (Budapest, Szent István Gimn., IV. o. t), 12. Fürjes Andor (Zalaegerszeg, Zrínyi Miklós Gimn., IV. o. t.), 13. Kondor Imre (Budapest, Trefort Ágoston Gimn., III. o. t.), 14. Czirók András (Miskolc, Földes Ferenc Gimn., IV. o. t.), 15. Kiss Róbert (Győr, Révai M. Gimn., III. o. t.), 16. Kőszegi Botond (Budapest, Fazekas Mihály Gimn., III. o. t.), 17. Tóth Csaba (Szolnok, Verseghy Ferenc Gimn., III. o. t.), 18. Egyedi Péter (Pécs, Leöwey Klára Gimn., IV. o. t), 19. Perlaki Tamás (Debrecen, Fazekas Mihály Gimn., IV. o. t.), 20. Jánosik János (Székesfehérvár, Teleki Blanka Gimn., IV. o. t.), 21. Szegő László (Szolnok, Verseghy Ferenc Gimn., IV. o. t), 22. Király Sándor Zsolt (Komló, Nagy Lajos Gimn., IV. o. t.), 23. Lakos Gyula (Budapest, Fazekas Mihály Gimn., III. o. t.), 24. Lénárt László (Kaposvár, Táncsics Mihály Gimn., IV. o. t.), 25. Zsuppán Sándor (Zalaegerszeg, Zrínyi Miklós Gimn., IV. o. t.), 26. Bilics Péter (Budapest, Fazekas Mihály Gimn., IV. o. t.), 27. Ujváry-Menyhárt Zoltán (Budapest, Fazekas Mihály Gimn., III. o. t.), 28. Czirják Gábor (Budapest, Fazekas Mihály Gimn., III. o. t.), 29. Piróth Attila (Budapest, Fazekas Mihály Gimn., III. o. t.), 30. Kertész Attila (Debrecen, Tóth Árpád Gimn., IV. o. t.), 31. Álmos Attila (Budapest, Berzsenyi Dániel Gimn., III. o. t.), 32. Matolcsi Máté (Budapest, Fazekas Mihály Gimn., III. o. t.).

A fizika III. kategória eredményei:
I. díj: Virág Ferenc (Ócsa, Bolyai János Gimn., IV. o. t., tanárai: Jarábik Béla és Beke István),
II. díj: Kovács Attila (Budapest, ELTE Apáczai Csere János Gyak. Gimn., III. o. t., tanára: Flórik György),
III. díj: Varga Péter (Kaposvár, Táncsics Mihály Gimn., IV o. t., tanára: Drankovics József),
4. Kocsis László (Sopron, Széchenyi István Gimn., IV. o. t., tanára: Légrádi Imre),
5. Bodor András (Budapest, ELTE Apáczai Csere János Gyak. Gimn., IV. o. t., tanára: Zsigri Ferenc),
6. Fehér Titusz (Budapest, József Attila Gimn., IV. o. t., tanára: Iván László),
7. Bakos Tamás (Eger, Gárdonyi Géza Gimn., IV. o. t., tanára: Leitner Györgyné),
8. Molnár Dénes (Debrecen, KLTE Gyak. Gimn., III. o. t., tanára: Szegedi Ervin),
9. Holpár Péter (Sopron, Berzsenyi Dániel Gimn., IV. o. t., tanára: dr. Lang Jánosné),
10. Futó Tibor (Budapest, Berzsenyi Dániel Gimn., IV. o. t., tanára: Hubert Györgyné).

További helyezettek:
11. Bob Zoltán (Győr, Czuczor Gergely Bencés Gimn., IV. o. t.), 12. Hegedűs Pál (Sopron, Berzsenyi Dániel Gimn., IV. o. t.), 13. Kukorelly Zsolt (Budapest, Szent István Gimn., IV. o. t.), 14. Maróti Miklós (Szeged, Radnóti Miklós Gimn., IV. o. t.), 15. Szabó Dénes (Budapest, ELTE Apáczai Csere János Gyak. Gimn., IV. o. t.), 16. Németh Péter (Pápa, Türr István Gimn., IV. o. t.), 17. Osvald Ákos (Kaposvár, Táncsics Mihály Gimn., IV. o. t.), 18. Papolczy Péter (Budapest, Berzsenyi Dániel Gimn., IV. o. t.), 19. Csizmadia Péter (Budapest, Móricz Zsigmond Gimn., IV. o. t), 20. Kővári Zoltán (Budapest, Szent István Gimn., IV. o. t.), 21. Kulcsár Béla (Kecskemét, Katona József Gimn., III. o. t.), 22. Kovács Ákos (Kecskemét, Katona József Gimn., IV. o. t.), 23. Bédi Sándor (Érd, Vörösmarty Mihály Gimn., IV. o. t.), 24. Stőhr Loránt (Budapest, ELTE Apáczai Csere János Gyak. Gimn., III. o. t.), 25. Bán Zoltán (Kecskemét, Katona József Gimn., IV. o. t.), 26. Harczos Gergely (Budapest, ELTE Apáczai Csere János Gyak. Gimn., IV. o. t.), 27. Szabó Jenő (Sárvár, Tinódi Gimn., IV. o. t.), 28. Baji Gál János (Gödöllő, Török Ignác Gimn., IV. o. t.), 29. Nagy Benedek (Debrecen, KLTE Gyak. Gimn., IV. o. t.), 30. Gáspár Ágnes (Kazincbarcika, Ságvári Endre Gimn., IV. o. t.), 31. Végh Zoltán (Kecskemét, Piarista Gimn., IV. o. t.).