| Cím: | 1991. Beszámoló az Eötvös-versenyről | ||
| Szerző(k): | Radnai Gyula | ||
| Füzet: | 1992/március, 129 - 133. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Eötvös Loránd (korábban Károly Irén) | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1991 október 18-án rendezte az Eötvös Loránd Fizikai Társulat a 68. Eötvös versenyt Budapesten és 12 vidéki városban. A budapesti verseny jól illeszkedett a centenáriumi ünnepségsorozathoz: a versenyre érkező diákok megtekinthették az aznap délelőtt megnyitott poszterkiállítást is. 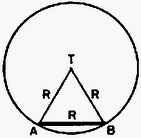 1. ábra 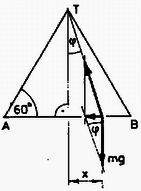 2. ábra A kitéréssel arányos nagyságú, de ellentétes irányú gyorsulása a harmonikus rezgőmozgást végző testnek van, vagyis a mókusnak úgy kell futnia, hogy mozgása harmonikus rezgőmozgás legyen. Ilyenkor ,,Hogyan kell egy bogárnak végigmásznia egy falhoz támasztott szalmaszálon, hogy ne csússzék el a szalmaszál, annak ellenére, hogy se a falnál, se a talajnál nincs súrlódás?'' Meglepő ötlettel állt elő az egyik versenyző a mostani Eötvös versenyen: legyen a létra végtelen nagy tömegű a mókushoz képest, akkor a mókus nyugodtan végigsétálhat rajta (ahogy egy légy is végigmászhat a létrán) anélkül, hogy mérhető módon megmozdulna a kerék Többen kísérleteztek azzal az ötlettel is, nem tud-e átugorni a mókus -ból -be úgy, hogy közben ne mozduljon meg a kerék. Úgy gondolták, hogy a kerék érintőjére merőlegesen kell elugrani -ból, és a -beli érintőre merőlegesen kell megérkezni a pontba. Azután gyorsan kiszállni a kerékből 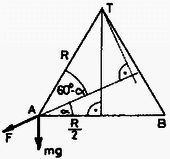 3. ábra Nézzük meg ennek az ,,ugró mókusnak'' az esetét kissé alaposabban! Tegyük fel, hogy az elugró mókust ideig állandó erő gyorsítja fel -ról sebességre az pontban, majd ugyanekkora, megfelelő erő fékezi le -ben (3. ábra). Jelöljük -val az elugrás sebességének a vízszintessel bezárt szögét! Ekkor az pontban a kerékre két erő hat: függőlegesen lefelé egy nagyságú erő, a sebességgel ellentétes irányban pedig . A két erő ellentétes forgató hatást fejt ki a kerékre, s az egyensúly feltétele: Kifejtve értékét: Jelöljük 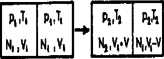 4. ábra Az állapotjelzők kezdetben mindkét oldalon a következők: A gázmolekulák száma kezdetben mindkét oldalon A rendelkezésre álló térfogat viszont legfeljebb A két egyenletbe az ismert adatokat behelyettesítve Érdekes, hogy Megjegyzés. A feladat megoldásának kulcsa a vízgőzre vonatkozó állapotegyenlet helyes felírása. Sok hibás megoldás abból keletkezett, hogy az összes víz elpárologását feltételezve határozták meg 3. Fémből készült, igen vékony falú, zárt gömbhéj belsejében fonálon egy kétrét hajtott alufóliacsík függ. A gömb két átellenes pontjára kívülről az ábrán látható módon feszültséget kapcsolunk (5. ábra). Megmozdul-e az alufóliacsík, s ha igen, hogyan? 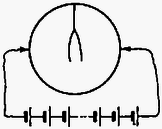 5. ábra Megoldás. A vékony gömbhéj ellenállása nem hanyagolható el. Lesz elektromos mező a gömb belsejében, mégpedig forgásszimmetrikus abban az esetben, ha a gömb belül üres. (A szimmetriatengely a csatlakozási pontokat összekötő átmérő.) 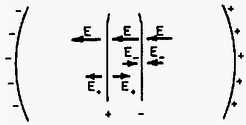 6. ábra Ha a gömb közepén ott van a kettéhajtott alufólia, akkor ezen megosztás jön létre azért, hogy a fólia ekvipotenciális legyen. A megosztott töltések tere kioltja a gömb belső terét a fólia két ága között (6. ábra). A fólia bármely ágára a külső Ezért a kettéhajlott fólia kinyílik, és egy olyan helyzetben állapodik meg, amikor már a rá ható elektromos, gravitációs stb. erők és forgatónyomatékok eredője egyaránt zérus. Ennek a feladatnak a helyes megoldására már csak két versenyző jött rá. Mivel ők az első két feladatot is jól megoldották, nem volt nehéz dolga a Versenybizottságnak, amikor az 1991. évi Eötvös verseny két első helyezettjét kellett kiválasztania. Az I. díjat egyenlő arányban megosztva nyerte BODOR ANDRÁS, az ELTE I. éves fizikus hallgatója, aki az ELTE Apáczai Csere János Gyakorló Gimnáziumban érettségizett, mint Zsigri Ferenc tanítványa, és KÁLI SZABOLCS, az ELTE I. éves fizikus hallgatója, aki Budapesten a Fazekas Mihály Gimnáziumban érettségizett, mint Horváth Gábor tanítványa. A két elsődíjas versenyző egyenként ötezer forint pénzjutalomban részesült. A II. és III. díjat a Versenybizottság összevonta és egyenlő arányban megosztotta a következő nyolc versenyző között: EGYEDI PÉTER, a BME I. éves villamosmérnök hallgatója, aki Pécsett a Leöwey Klára Gimnáziumban érettségizett, mint Csikós Istvánné és Kotek László tanítványa; GEFFERTH ANDRÁS, a budapesti Fazekas Mihály Gimnázium III. osztályos tanulója, Tóth László és Horváth Gábor tanítványa; KATZ SÁNDOR, a bonyhádi Petőfi Sándor Gimnázium III. osztályos tanulója, Erdélyesi János tanítványa; KŐSZEGI BOTOND, a budapesti Fazekas Mihály Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa; MIKLÓS GYÖRGY, a BME I. éves villamosmérnök hallgatója, aki Budapesten a Szt. István Gimnáziumban érettségizett, mint Kovács István tanítványa; NAGY BENEDEK, a KLTE I. éves fizikus hallgatója, aki Debrecenben a KLTE Gyakorló Gimnáziumban érettségizett, mint Dudics Pál tanítványa; RÓZSA BALÁZS, a budapesti Fazekas Mihály Gimnázium IV. osztályos tanulója, Horváthné Dvorák Cecília tanítványa és SZENDRŐI BALÁZS, a budapesti Fazekas Mihály Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa. A fenti nyolc versenyző egyenlő helyezésben a verseny 3 ‐ 10. helyezettje, pénzjutalmuk ezer-ezer forint. Dicséretet és ötszáz‐ötszáz forint jutalmat kapott az alábbi hat versenyző: ÁLMOS ATTILA, a budapesti Berzsenyi Dániel Gimnázium IV osztályos tanulója, Istók Katalin tanítványa; BONCZ ANDRÁS, az ELTE I. éves matematikus hallgatója, aki Zalaegerszegen a Zrínyi Miklós Gimnáziumban érettségizett, mint Pálovics Róbert tanítványa; EGEDI PÉTER, a szegedi Radnóti Miklós Gimnázium IV. osztályos tanulója, Mike János tanítványa; NAGY GYULA, a jászberényi Erősáramú Szakközépiskola IV. osztályos tanulója, Bakki Árpád tanítványa; NEMES NORBERT MARCELL, a budapesti Fazekas Mihály Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa és SOMLAI ÁKOS, a BME I. éves villamosmérnök hallgatója, aki Pécsett a Nagy Lajos Gimnáziumban érettségizett, mint Orovicza Márkné tanítványa. További helyezéseket a Versenybizottság nem állapított meg. Az ünnepélyes eredményhirdetésre 1991. november 29-én délután került sor az ELTE Főépületének fizikai előadótermében, ahol a fennállásának századik évfordulóját ünneplő Társulat egyik alelnöke adta át a díjakat és a Társulat által felajánlott pénzjutalmat. A nyertes versenyzők és tanáraik, valamint az érdeklődő hallgatóság a harmadik feladathoz kapcsolódó kísérletsorozattal győződhettek meg ugyanitt a már kikövetkeztetett megoldás helyességéről. |