Cím:	A vízhullámok
Szerző(k):	Gnädig Péter
Füzet:	1992/február, 81 - 86. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A vízhullámok${}^{*}$   Ha egy test (vadkacsa, motorcsónak, tartályhajó) állandó sebességgel mozog a víz felszínén, az általa keltett vízhullámok jellegzetes, ék alakú mintázatban követik a hullámforrást. A hullámkép meglehetősen összetett, az ék két szárát madártollra emlékeztető kis hullámok alkotják (1.ábra).     1. ábra   Vajon hogyan függ az ék $\alpha$-val jelölt félnyílásszöge a hullámforrás sebességétől? Ezt a kérdést tanulmányozhatjuk kísérleti eszközökkel (lásd a 137. mérési feladat megoldását lapunk 94. oldalán), vagy megpróbálhatjuk elméleti megfontolásokkal "kitalálni'' $\alpha$ értékét. (Természetesen ez utóbbi esetben össze kell vetnünk megfontolásaink eredményét a kísérleti tényekkel.)   Hangrobbanás, Cserenkov sugárzás   Első ‐ legtermészetesebb ‐ gondolatunk az lehet, hogy a vízhullámok kúpszöge is a hangtanból ismerős módon származtatható. Ha egy hangforrás (például egy repülőgép) a $c$ hangsebességet meghaladó $v$ sebességgel mozog, a különböző időpillanatokban keltett hullámainak burkolófelülete egy kúp lesz, melynek fél-nyílásszögét a $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{c}{v}}\end{array}$ (1) képletből kaphatjuk meg (2.ábra). A hangrobbanás egyik fajtájának jelenségét éppen akkor észleljük, amikor a $QP$ hullámfront eléri a megfigyelő személyt. 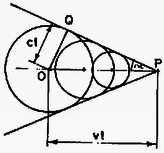    2. ábra   Érdekes megjegyezni, hogy a hangrobbanásnak megfelelő jelenség a fénynél is megfigyelhető minden olyan esetben, amikor egy fényforrás a fénysebességnél nagyobb sebességgel mozog. Hát ez meg hogyan lehetséges? ‐ kérdezhetjük. Nem a fénysebesség a létező legnagyobb sebesség a természetben? De igen, a vákuumbeli fénysebesség a határsebesség, ennek értéke $c_0=300000\text{km/s}$. Anyagokban (üvegben, vízben, átlátszó kristályokban) azonban a fény lassabban terjed, csupán $c=c_0/n$ sebességgel, ahol $n$ az anyag törésmutatója. Vízre például $n=4/3$, a fény tehát a vízben csak $c=225000\text{km/s}$ sebességgel "halad''. Ha egy elektromosan töltött atomi részecske (elektron, pozitron, proton, $\alpha$-részecske) mondjuk $v=250000\text{km/s}$ sebességgel halad át a vizen, "fényrobbanás'' jelensége lép fel, s a "fénykúp'' szögét a hangrobbanáshoz hasonlóan az (1) összefüggésből számolhatjuk ki. Ezt a jelenséget felfedezőjéről Cserenkov-sugárzásnak nevezték el, és manapság kiterjedten alkalmazzák elemi részecskék sebességének mérésénél.   Dimenzióanalízis ‐ meglepő eredménnyel   Térjünk most vissza a vízhullámokhoz! Vajon megmagyarázható-e a vizen mozgó test által keltett hullámkép is az előzőek mintájára? Nem! A táblázatokban hiába keressük a vízhullámok terjedési sebességét, ilyen adatot nem találunk, mégpedig azért, mert a vízhullámok terjedése nem írható le egyetlen sebesség-adattal. A hangtól és a fénytől eltérően a vízhullámok sebessége erősen függ attól, hogy milyen hullámhosszúságú hullámok terjedéséről van szó. Ez a diszperzió jelensége, ami kismértékben a fény terjedésénél is fellép (hiszen az anyagok törésmutatója általában függ a fény színétől, tehát a frekvenciájától, a hullámhosszától), a vízhullámoknál azonban sokkal lényegesebb, meghatározó szerepet játszik. Az is mutatja a víz és a hanghullámok különbözőségét, hogy a 2. ábrán látható kúpképződés esetén a hullámfront (például a hullámhegyek pillanatnyi helyzetét jelző vonal) a $PQ$ egyenessel párhuzamos lenne, nem pedig a kísérletileg jól megfigyelhető madártoll-mintázat (1.ábra). A "csónakhullámok'' magyarázatát tehát máshol kell keresnünk! Induljunk el egészen más úton, próbáljuk meg a "dimenzióanalízis'', vagyis a mértékegységek tanulmányozása segítségével kitalálni, hogyan függhet $\alpha$ nagysága a $v$ sebességtől. Vajon milyen adatok, paraméterek határozzák meg $\alpha$ értékét? Nyilván függhet a szög a $g$ nehézségi gyorsulástól, valamint a víz $\varrho$ sűrűségétől, hiszen ezek együtt felelősek a "kidomborodó'' vízfelületet visszahúzó erőkért, vagyis a vízhullámok kialakulásáért. Elvben szerepet játszhat még a felületi feszültség, de ez csak az erősen görbült vízfelszínre, tehát az igen rövid hullámhosszúságú hullámokra lehet hatással. Ugyancsak figyelmen kívül hagyhatjuk a folyadék belső súrlódását, a viszkózitás jelenségét, ez csak a hullámok csillapodását szabja meg, a terjedésüket csak közvetve befolyásolja. Ha sikerült meggyőzni magunkat arról, hogy $\alpha$ csak $v$, $g$ és $\varrho$ függvénye (a dimenzionális megfontolásoknál ez a legkényesebb lépés!), akkor már majdnem célba értünk. Írjuk fel a különböző mennyiségek mértékegységét:$\left[v\right]=\text{m/s}$, $\left[g\right]={\text{m/s}}^2$, $\varrho ={\text{kg/m}}^3$ és végül $\left[\alpha \right]=1$. A kg mértékegység csak $\varrho$-ban szerepel, s mivel a keresett szög dimenziótlan, arra kell következtetnünk, hogy $\alpha$ nem függhet $\varrho$-tól. Hasonló érveléssel adódik, hogy $g$ sem szerepelhet $\alpha$ formulájában, s akkor a $v$ sebesség sem jelenhet meg a képletben. A hullám-ék nyílásszöge tehát $\begin{array}{c}{\displaystyle \alpha \left(v\mathrm{,}\varrho \mathrm{,}g\right)={\alpha }_0=\text{állandó}}\end{array}$ kell legyen! Ezt a meglepő következtetést, mármint azt, hogy $\alpha$ egyáltalán nem függhet a hullámforrás sebességétől, a kísérleti adatok is alátámasztják: elegendően nagy felületú és elegendően mély víz felszínén viszonylag gyorsan mozgó test hullámkúpjának szöge a test sebességétől független, s a félszög nagysága kb. ${20}^{\circ }$. Mozoghat a csónak közepes sebességgel, vagy nagyon gyorsan, végezhetjük a kísérletet a Földön vagy a Holdon, vízben vagy olajban, ez a szög mindig ${20}^{\circ }$ körüli érték lesz. Vajon miért éppen ekkora?   Diszperzió, fázissebesség, csoportsebesség   A továbbiakban le szeretnénk vezetni egy olyan egyenletet, amelyből kiszámítható ${\alpha }_0$ számértéke. Ehhez természetesen túl kell lépnünk az egyszerű dimenziós megfontolásokon, és fel kell idéznünk a hullámtan néhány fontos jelenségét, fogalmát. A címben szereplő kifejezések közül a diszperzióról volt már szó, most ismerkedjünk meg másik két fogalommal is. (Azok, akiknek a fázissebesség és a csoportsebesség fogalma, kiszámítási módja jól ismert, nyugodtan átugorhatják ezt a fejezetet.) Hogyan lehet matematikailag leírni egy hullámot (például a vízfelszín alakját) a $t$ időkoordináta és az $x$-szel jelölt térbeli koordináta segítségével? Például így: $\begin{array}{c}{\displaystyle H\left(x\mathrm{,}t\right)=A\text{cos}\left(k\cdot x-\omega \cdot t\right)\mathrm{,}}\end{array}$ (2) ahol $H$ a vízfelszín "kiemelkedési magassága'', $A$, $k$ és $\omega$ pedig állandók. Az $A$ mennyiség a hullám legnagyobb kitérését, a hullám amplitúdóját adja meg. A $k$ szám a hullám térbeli periodicitását fejezi ki, neve: hullámszám, kapcsolata a $\lambda$ hullámhosszal: $k=2\pi \lambda$ (igazoljuk!). Az $\omega$ mennyiség az időbeli változás ütemét jellemző körfrekvencia, amely a $T$ periódusidőből az $\omega =2\pi /T$ képlet segítségével számítható ki (ellenőrizzük!). 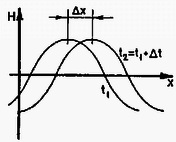    3. ábra   Ha lerajzoljuk a hullámképet valamely $t_1$ pillanatban, majd egy kicsit későbbi $t_2=t_1+\Delta t$ pillanatban (3 ábra), azt látjuk, hogy a hullámhegyek csúcsai egy bizonyos $\Delta x$ távolsággal odébbtolódtak. Mivel a hullámhegyek csúcsát jól meghatározott "fázisérték'' jellemzi (a koszinusz függvény argumentuma $2\pi$ egész számú többszöröse kell legyen), (2)-ből leolvasható, hogy $k\cdot \Delta x=\omega \cdot \Delta t$  teljesül. Ebből következik, hogy a hullámok azonos fázisú pontjainak (például a hullám hegyeinek vagy a csomópontjainak) haladási sebessége: $\begin{array}{c}{\displaystyle v_{\text{fázis}}=\frac{\Delta x}{\Delta t}=\frac{\omega }{k}\mathrm{.}}\end{array}$ A diszperzió jelensége ‐ vagyis a fázissebesség hullámhossz-függősége ‐ úgy fogalmazható meg, hogy $\omega$ valamilyen (általában bonyolult, nemlineáris) függvénye $k$-nak, s emiatt a $\begin{array}{c}{\displaystyle v_{\text{fázis}}\left(k\right)=\frac{\omega \left(k\right)}{k}}\end{array}$ (3) is hullámszámfüggő (vagyis hullámhosszfüggő) mennyiség lesz. 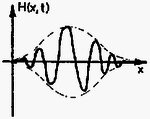    4. ábra   Ha különböző hullámhosszúságú (különböző hullámszámú) hullámokat "összeadunk'', egymásra "szuperponálunk'', akkor a végtelen hosszúságban elnyúló szinuszhullám helyett egy véges méretű hullámvonulatot, ún. hullámcsomagot kapunk (4. ábra). Vajon hogyan mozog egy hullámcsomag, hogyan változtatja helyét (és esetleg az alakját) az idő múltával? A hullámvonulat egyes összetevői, elemi szinuszhullámai $v_{\text{fázis}}$ sebességgel haladnak, de a hullámcsomag egészének (átlagos) sebessége ettől eltérő is lehet. Az, hogy mekkora, a következő egyszerű gondolatmenettel deríthető ki. Adjunk össze két azonos amplitúdójú, de kicsit eltérő hullámszámú (tehát kicsit eltérő hullámhosszúságú és emiatt kicsit eltérő körfrekvenciájú) hullámot: $\begin{array}{c}{\displaystyle H\left(x\mathrm{,}t\right)=A\cdot \text{cos}\left(k_{1}x-{\omega }_{1}t\right)+A\cdot \text{cos}\left(k_{2}x-{\omega }_{2}t\right)\mathrm{.}}\end{array}$ Alkalmazzuk ezekután az ismert $\text{cos}\alpha +\text{cos}\beta =2\text{cos}\frac{\alpha +\beta }{2}\cdot \text{cos}\frac{\alpha -\beta }{2}$ azonosságot, és használjuk az $\left({\omega }_1+{\omega }_2\right)/2=\omega$, $\left(k_1+k_2\right)/2=k$, ${\omega }_1-{\omega }_2=\Delta \omega$, $k_1-k_2=\Delta k$ jelöléseket. Ezzel a teljes hullámra $\begin{array}{c}{\displaystyle H\left(x\mathrm{,}t\right)=2A\cdot \text{cos}\left(kx-\omega t\right)\cdot \text{cos}\left(\frac{\Delta k}{2}x-\frac{\Delta \omega }{2}t\right)}\end{array}$ (4) adódik.     5. ábra   A fenti összefüggésből leolvashatjuk, hogy a szuperpozíció során kialakuló hullámkép olyan hullámcsomagokat tartalmaz, amelyek $t_0$ idő alatt $x_0=\frac{\Delta \omega }{\Delta k}\cdot t_0$ távolsággal tolódnak odébb (5.ábra), tehát $\begin{array}{c}{\displaystyle v_{\text{csoport}}=\frac{\Delta \omega \left(k\right)}{\Delta k}}\end{array}$ (5) sebességgel haladnak. A hullámcsomag csoportsebessége az $\omega \left(k\right)$ diszperziós függvény "differenciahányadosával'', kicsiny $\Delta k$ esetén pedig jó közelítéssel $\omega \left(k\right)$ deriváltjával egyenlő. (A deriváltat az átlagos hullámszám értékénél kell kiszámítanunk.) A fenti egyszerű, mindössze két tagból álló szuperpozíciónál a hullámkép nem egyetlen hullámcsomagból, hanem periódikusan ismétlődő csomagokból áll. (Ez a lebegés jelensége a hullámtanban.) Bonyolultabb hullámösszetevéssel valódi hullámcsomag is előállítható, s ennek terjedési sebességére is az (5) egyenlet érvényes.     6. ábra   A kétféle hullámsebesség, a fázis és a csoportsebesség általában különböző nagyságú lehet. A fázissebességet az $\omega \left(k\right)$ függvény adott pontbeli (adott $k$-hoz tartozó) szelőjének meredeksége, a csoportsebességet pedig a hullámcsomag átlagos hullámszámú pontjához tartozó érintőjének meredeksége adja meg (6. ábra): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle v_{\text{fázis}}}& {\displaystyle =\frac{\omega }{k}=\text{tg }\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle v_{\text{csoport}}}& {\displaystyle =\frac{\Delta \omega }{\Delta k}\text{tg }\beta \mathrm{.}}\hfill \end{array}}$ Megjegyezzük, hogy fénynél vagy hangnál az $\omega \left(k\right)$  függvény jó közelítéssel lineáris, $\omega \left(k\right)=c\cdot k$, ahol $c$ egy állandó. Ilyen esetben $v_{\text{fázis}}=v_{\text{csoport}}=c$.    Hajóhullámok és a Thalész-kör   Foglalkozzunk most ismét az eredeti problémánkkal, a vízhullámokkal! Vajon milyen kapcsolat áll fenn a $k$ hullámszám és az $\omega$ körfrekvencia között a földi nehézségi erőtér hatására kialakuló ún. nehézségi vízhullámoknál? A bonyolult hidrodinamikai számítások helyett hívjuk segítségül ismét a dimenzióanalízis módszerét! Feltételezhetjük, hogy $\omega$ a $k$ hullámszámon kívül csak a $g$ nehézségi gyorsulástól függ (gondoljuk végig, mi mástól függhetne még), s mivel $\left[\omega \right]=s^{-1}\mathrm{,}\left[k\right]=m^{-1}\mathrm{,}\left[g\right]=m\cdot s^{-2}$, a keresett függvénykapcsolat csakis $\begin{array}{c}{\displaystyle \omega \left(k\right)=A\cdot \sqrt[]{gk}}\end{array}$ (6) alakú lehet, ahol $A$ egy dimenziótlan állandó. Részletes számítások szerint $A=1$. (Felhasználtuk, hogy a víz elég nagy és elég mély, továbbá hogy a hullámok nem nagyon kicsi hullámhosszúságúak, ezért a felületi feszültség nem játszik lényeges szerepet.) A (6) összefüggésből kiszámíthatjuk a vízhullámok fázis- és csoportsebességét: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle v_{\text{fázis}}}& {\displaystyle =\frac{\omega }{k}=A\cdot \sqrt[]{\frac{g}{k}}\mathrm{,}}\hfill \\ \hfill {\displaystyle v_{\text{csoport}}}& {\displaystyle =\frac{\Delta \omega }{\Delta k}=A\cdot \sqrt[]{g}\frac{\sqrt[]{k_1}-\sqrt[]{k_2}}{k_1-k_2}=\frac{A\cdot \sqrt[]{g}}{\sqrt[]{k_1}+\sqrt[]{k_2}}\approx \frac{1}{2}A\cdot \sqrt[]{\frac{g}{k}}\mathrm{.}}\hfill \end{array}}$ A vízhullámok erős diszperziót mutatnak, terjedési sebességük nem adható meg egyetlen számmal, hanem csak egy függvénnyel jellemezhető. Mindkét hullámsebesség arányos a hullámhossz négyzetgyökével, tehát a nagy hullámhosszúságú (lomha) hullámok gyorsabban, a rövidebbek pedig lassabban terjednek. Érdekes és a továbbiak szempontjából fontos észrevétel, hogy a nehézségi vízhullámokra fennáll a $\begin{array}{c}{\displaystyle v_{\text{csoport}}=\frac{1}{2}{v}_{\text{fázis}}}\end{array}$ (7) összefüggés. 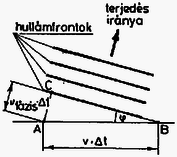    7. ábra   Amikor egy hullámforrás (hajó, csónak, vizisíző) mozog, a mozgása során nem csak egyféle, hanem különböző hullámhosszúságú (hullámszámú) vízhullámokat kelt, s ezek különböző sebességgel terjednek. Válasszunk ki egy bizonyos $k$ hullámszámot, ehhez tartozik egy $v_{\text{fázis}}$ adat, a hullámok azonos fázisú pontjainak haladási sebessége. Ha a hullámforrás $v$ sebességgel halad, akkor egy bizonyos $\Delta t$ idő alatt a 7. ábrán látható $A$ pontból az attól $v\cdot \Delta t$ távol levő $B$ pontba jut, az $A$-ban keltett hullám azonos fázisú pontja pedig a $v_{\text{fázis}}\cdot \Delta t$ távol levő $C$ pontba. A $C$ pontban tehát a $B$ pontbelivel azonos fázisú a hullám, s ez igaz a $BC$ egyenes minden pontjára. A hullámfrontok tehát olyan egyenesek, melyeknek a hullámforrás sebességével bezárt $\phi$ szögére fennáll a $\begin{array}{c}{\displaystyle \text{sin}\phi =\frac{v_{\text{fázis}}}{v}}\end{array}$ (8) összefüggés. Mivel a hullám terjedési iránya a hullámfrontokra merőleges, a terjedés iránya a csónak sebességvektorával $\frac{\pi }{2}-\phi$ szöget zár be. Mivel a $v_{\text{fázis}}$ sebesség függ a hullámszámtól, a különböző hullámhosszúságú elemi hullámok sebességének mind a nagysága, mind pedig az iránya különböző lehet. 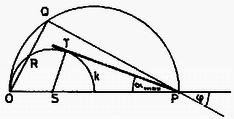    8. ábra   Tekintsük most a hullámforrás véges idejű, mondjuk $1$ másodpercnyi mozgását. Ha a csónak kezdetben az $O$ pontban volt, és $1$ s alatt a $P$ pontba jutott (8.ábra), akkor az $O$ pontban keltett hullámok különböző, a fázissebességüktől függő $\overrightarrow{OQ}$ irányokba indulnak el. A különböző $Q$ pontok egy félkörön, az $OP$ átmérőhöz tartozó Thalészkörön helyezkednek el. Mindegyik hullámhosszúsághoz (pontosabban fogalmazva: mindegyik hullám- hosszúság-intervallumhoz) tartozik egy bizonyos nagyságú csoportsebesség. Ha egy hullámcsomag átlagos fázissebességével haladva $1$ s alatt az $O$ pontból a $Q$-ba érnénk el, akkor maga a hullámcsomag ennyi idő alatt csak az $R$ pontig jut, ahol (7) miatt $OR=\frac{1}{2}\cdot OQ$. Az $R$ pontok mértani helye tehát egy olyan Thalész-kör, melynek sugara $OS=\frac{1}{4}\cdot OP$. Gondoljuk azt, hogy a $P$ pontbeli csónakban ülünk, és visszatekintünk a csónak által keltett hullámképre. A különböző (átlagos) hullámhosszúságú hullámcsomagokat a $k$ kör különböző $R$ pontjaiban észleljük, vagyis a csónak haladási irányához képest különböző $\alpha$ szögekben látjuk. Ezen $\alpha$ szögek között van egy legnagyobb, a $k$-t érintő $PT$ egyenesnek megfelelő ${\alpha }_{\text{max}}$, amelyre fennáll, hogy $\begin{array}{c}{\displaystyle \text{sin}{\alpha }_{\text{max}}=\frac{TS}{SP}=\frac{1}{3}\mathrm{,}}\end{array}$ azaz ${\alpha }_{\text{max}}=\mathrm{19,}{5}^{\circ }$. Ekkora fél-nyílásszögű ék alakjában követik a hullámforrást a vízhullámok, függetlenül a hullámforrás sebességétől. A tapasztalat szerint az elegendően gyorsan mozgó motorcsónakok, hajók valóban kb. ${20}^{\circ }$-os félszögű "kúpot'' húznak maguk után, összahangban a fenti (először a múlt század végén Rayleigh angol fizikus által kidolgozott) elméleti megfontolásokkal. Kisebb, $\mathrm{0,5}\text{ m/s}$ alatti sebességeknél viszont a hullámkép határozottan eltér az elmondottaktól, az ék szöge a sebesség csökkenésével egyre nagyobbá válik. Ennek az az oka, hogy kis csónaksebességnél a kicsiny fázissebességű, tehát a kicsiny hullámhosszúságú hullámok a leglényegesebbek, ezek terjedését pedig erősen befolyásolja a felületi feszültség. Dimenzionális megfontolásokból azt kapjuk, hogy a felületi feszültség által létrejövő ún. kapilláris hullámokra $\begin{array}{c}{\displaystyle \omega \left(k\right)=\text{állandó}\cdot \sqrt[]{\frac{\sigma k^3}{\varrho }}\mathrm{,}}\end{array}$ (9) ahol $\sigma$ a felületi feszültség, $\varrho$ pedig a víz sűrűsége. Ezeknél a hullámoknál az igaz, hogy $v_{\text{fázis}}\sim \sqrt[]{k}\sim \frac{1}{\sqrt[]{\lambda }}$, tehát a rövidebb hullámok terjednek gyorsabban. A kapilláris hullámok és a nehézségi hullámok érvényességi tartományának $k_0$ határát a (6) és a (9) diszperziós reláció összevetéséből kaphatjuk meg (a dimenziótlan állandókat egynek választhatjuk, hiszen nem pontos számítást, csupán nagyságrendi becslést végzünk): $\begin{array}{c}{\displaystyle \sqrt[]{\frac{\sigma k\genfrac{}{}{0ex}{}{3}{0}}{\varrho }}=\sqrt[]{g{k}_0}\mathrm{,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle k_0=\sqrt[]{\frac{\varrho g}{\sigma }}\approx 400\frac{1}{\text{m}}\mathrm{,}}\end{array}$ az ennek megfelelő sebesség pedig $\begin{array}{c}{\displaystyle v_0\approx \sqrt[]{\frac{g}{k_0}}\approx \mathrm{0,2}\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$ A csónaksebességtől független hullámkép csak $v_0$-nál számottevően nagyobb, legalább $\text{m/s}$-os hullámforrás-sebesség esetében várható. Ezt a várakozásunkat igazolják a 137. mérési feladat eredményei is.   Gnädig Péter ELTE Atomfizikai Tanszék ${}^{*}$Előadás az 1992. évi Téli Fizikai Ankéton