Cím: 1991. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):  Surányi János 
Füzet: 1992/február, 61 - 66. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Legyen n pozitív egész, a,b≥1,c>0 valós számok. Bizonyítandó, hogy

(ab+c)n-c(b+c)n-c≤an.
 

I. megoldás. A nevező pozitív, mert a feladat feltételei mellett b+c>1, és így
(b+c)n≥b+c>c.
Elegendő ennek folytán a nevezővel átszorozva keletkező
(ab+c)n-c≤an(b+c)n-anc(1)
egyenlőtlenséget bizonyítani. Ezt teljes indukcióval tesszük. Az n=1 esetben egyenlőség áll fenn. Jelöljük a bal oldalt An-nel, a jobb oldalt Bn-nel. Tegyük fel, hogy n-nek valamilyen m értékére Am≤Bm, és nézzük meg, mennyivel változik az egyik oldal, mennyivel a másik, ha m-et eggyel növeljük.
Am+1-Am=(ab+c)m(ab+c-1).Bm+1-Bm=am(b+c)m(ab+ac-1)-am(a-1)c.


Az ab+ac-1 különbségről a könnyebb összehasonlítás érdekében ab+c-1-re térve, majd az első tag első és második tényezőjét egy hatvánnyá alakítva az utóbbi különbség így írható:
Bm+1-Bm=am(b+c)m(ab+c-1)+am(b+c)m(ac-c)-am(a-1)c==(ab+ac)m(ab+c-1)+am(a-1)c[(b+c)m-1].
Itt az első tag nagyobb az Am+1-Am különbségnél, ha a>1, mert ab+ac>ab+c, a második pedig pozitív. Így
Bm+1-Bm>Am+1-Am, azaz Bm+1-Am+1>Bm-Am.
Indukciós feltevésünk szerint a jobb oldal nem negatív, így a bal pozitív. Ezzel azt láttuk be, hogy ha (1) teljesül egy n értékre, és a>1, akkor minden nagyobb értékre már szigorú egyenlőtlenség érvényes (1)-ben.
Mivel n=1-re egyenlőség áll (az eredeti egyenlőtlenségben minden a,c és 0-tól különböző b értékre), így (1)-ben és az eredeti egyenlőtlenségben is a< jel érvényes minden 1-nél nagyobb n egészre és 1-nél nagyobb a-ra.
Ha a=1, akkor egyenlőtlenségeink egyenlőségbe mennek át. Ezzel a feladat állítását igazoltuk, és tisztáztuk azt is, hogy milyen esetekben áll fenn egyenlőség.
 

II. megoldás. Feltehetjük, hogy n>1 és a>1, mert n=1 esetén a két oldal egyenlő, bármi is a, és hasonlóan egyenlőség áll fenn a=1 esetén minden n-re. Az (1) egyenlőtlenséget bizonyítjuk. Rendezzük át a következő módon:
c(an-1)≤[a(b+c)]n-(ab+c)n.(2)
Alkalmazzuk mindkét oldalra az n≥2 esetén érvényes
un-vn=(u-v)(un-1+un-2v+...+uvn-2+vn-1)
azonosságot. A jobb oldalon az alapok különbsége c(a-1), így a bizonyítandó állítás a következő alakot ölti:
c(a-1)(an-1+an-2+...+a+1)≤c(a-1)[(an-1(b+c)n-1++an-2(b+c)n-2(ab+c)+...+a(b+c)(ab+c)n-2+(ab+c)n-1].


Itt a vizsgált esetben c(a-1) pozitív, a zárójel j-edik tagjában pedig aj a bal oldalon 1-gyel van szorozva, a jobb oldalon viszont
ab+c>b+c>1
folytán 1-nél nagyobb számmal. Az utolsó egyenlőtlenség tehát a vizsgált esetekben szigorú egyenlőtlenséggel helyes.
Csupa ekvivalens átalakítást végeztünk, tehát a bizonyítandó egyenlőtlenség is szigorú egyenlőtlenséggel érvényes, kivéve, ha n=1, továbbá ha a=1. Ezzel az előző megoldásban is nyert, valamivel élesített állítást nyertük.
 

Megjegyzések: 1.Figyeljük meg, hogy mind a nevező pozitív voltának a belátásánál, mind az (1) egyenlőtlenség bizonyításánál csak annyit használtunk, hogy b+c≥1, b>0, így elég lett volna csak ennyit tenni fel b≥1 helyett.
2. A (2) egyenlőtlenséget beláthatjuk úgy is, hogy a jobb oldalt a binomiális tétel szerint kifejtjük és a b egyenlő hatványait tartalmazó tagokat összevonjuk. Ekkor a legmagasabbfokú tag kiesik, a következő
nan-1bn-1(a-1)c,
a többiben pozitív tényezők ak-1-gyel vannak szorozva (k=2,...,n), ami pozitív. A bal oldalt a fenti módon alakítva szorzattá (a-1)c szorzója egy n-tagú összeg, aminek a tagjai a-nak n-nél kisebb kitevőjű hatványai, és így nem nagyobbak an-1-nél, tehát an-1bn-1-nél sem. Az egyenlőtlenség tehát teljesül.
 

III. megoldás. A feladat annak a belátását kívánja, hogy a
P(x)=xn-(bx+c)n-c(b+c)n-c
polinom olyan függvényt állít elő, amelyik nemnegatív, ha x értéke legalább 1.
Ha n=1, akkor a 0 polinommal van dolgunk, hacsak b≠0.
Ha n≥2, akkor P(1)=0. Így az állítás bizonyításához elég azt megmutatni, hogy a függvény növekszik, x≥1, ehhez pedig azt, hogy a deriváltja pozitív ezekre az értékekre. A derivált
P'(x)=n(xn-1-b(bx+c)n-1(b+c)n-c)=n(xn-1(b+c)n-cxn-1-b(bx+c)n-1)(b+c)n-c.

A nevezőre a binomiális tételt alkalmazva
(b+c)n-c=bn+nbn-1c+...+cn-c>bn+nbn-1c-c==bn+(nbn-1-1)c>bn>0.

A számlálót így írhatjuk:
n(b[(bx+cx)n-1-(bx+c)n-1]+cxn-1[(b+c)n-1-1)]).
Itt, mivel n≥2,x≥1 és b+c>1,
bx+cx≥bx+c≥b+c>1,
tehát az első különbség nemnegatív, a második pozitív, és így a számláló is pozitív, tehát P' is, és ezt akartuk belátni.
 
2. Egy konvex testnek két háromszöglapja és három négyszöglapja van. Kössük össze az egyik háromszöglap mindegyik csúcsát a vele szemközti négyszöglap átlóinak metszéspontjával. Bizonyítsuk be, hogy a három egyenes egy ponton megy át.
 

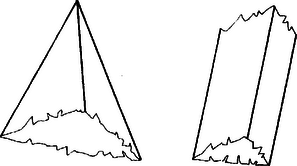
Megoldás. Meg kell határoznunk a test alakját. Egy négyszöglap éleihez csatlakozik mind a négy további lap. Mivel a test konvex, így a testet a négyszöglapok síkjai által határolt egyik konvex térrészből a háromszöglapok síkjai metszik ki.
 
 

1. ábra
 

Ez a térrész egy triéder (háromoldalú testszöglet, amelyiknek a lapszögei 180∘-nál kisebbek), vagy végtelen, háromoldalú hasáb (1.ábra). Ennek a határlapjain a további két metsző sík között négyszögeknek kell keletkezniük, tehát a két sík metszésvonalának a térrészen kívül kell lennie, vagy párhuzamos a két sík. A háromszöglapoknak tehát nincs közös pontja.
Legyenek ezek a lapok A1B1C1 és  A2B2C2, a további élek pedig A1A2, B1B2, C1C2 (2. ábra). Jelöljük a B1B2C2C1, C1C2A2A1, A1A2B2B1 lapok átlóinak a metszéspontját rendre A3, B3, C3-mal, és nézzük az A1A3,B1B3,C1C3 egyeneseket.
 
 

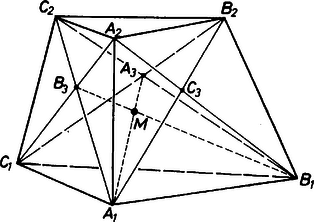2. ábra
 

Az A1B1C2 síkmetszet B1C2 oldalának belső pontja A3,A1C2-nek pedig B3, így A1A3 és B1B3 metszi egymást a háromszög belsejének egy M pontjában. Hasonlóan látható, hogy C1C3 is metszi A1A3-at is, B1B3-at is. Az A1B1C2 síknak egyik oldalára esik C1, a másikra A2 és B2, tehát C1 és C3 is ellenkező oldalára esik. C1C3-nak tehát egy közös pontja van a síkkal, és így csak akkor metszheti A1A3-at is, B1B3-at is, ha ez a pont M. A három egyenes tehát egy ponton megy keresztül, és ezt kellett bizonyítanunk.
 

Megjegyzések: 1. A megoldást többen arra a tételre hivatkozva fejezték be, hogy ha három egyenes páronként metszi egymást, akkor vagy egy síkban vannak, vagy egy ponton mennek keresztül. Ez igaz három helyett akárhány egyenesre, és így látható be. Ha egy ponton mennek át az egyenesek, akkor igaz az állítás. Ha ez nem áll, akkor vegyünk egy P metszéspontot. Egy e egyenes, amelyik nem megy át P-n, a P-n átmenő egyeneseket (tehát legalább két egyenest) P-től különböző pontban metsz. Ekkor azonban a P-n átmenő egyenesek benne vannak a P és e által meghatározott síkban. Ebben a síkban minden további egyenes is benne van, hiszen különböző pontokban metsz legalább két P-n átmenő egyenest.
2. A feladat megoldásában valójában három metsző síkról van szó, az A1B1C2 háromszögén kívül az A1B2C1 és az A2B1C1 háromszög síkjáról. A fenti megoldás egy változatához jutunk, ha azt látjuk be, hogy A1A3,B1B3 és C1C3 ezek közül rendre két-két sík metszésvonala, és ezek nem lehetnek párhuzamosak.
3. Bár a megoldás során ismételten hivatkoztunk a test konvex voltára, ez többnyire csak bizonyos metszéspontok létrejöttének a biztosításához kellett. Felmerül a kérdés, hogy ez nem biztosítható-e egyszerűbb feltételekkel is. Ennek végiggondolását az olvasóra hagyjuk.
4. A feladat megfogalmazható síkbeli feladatként, csak azt kell figyelembe venni, hogy a test alakját vizsgálva arra jutottunk, hogy A1A2,B1B2 és C1C2 egy ponton megy keresztül, vagy párhuzamosak. A feladat tehát így szól: Az A1A2, B1B2, C1C2 egyenesek egy ponton mennek keresztül, vagy párhuzamosak. A1B2 és B1A2, B1C2 és C1B2, C1A2 és A1C2 metszéspontját sorra C3, A3, B3-mal jelölve bizonyítandó, hogy A1A3, B1B3 és C1C3 egy ponton megy keresztül, vagy párhuzamosak. (Feltesszük, hogy A3, B3 és C3 létrejön.) Bizonyításra kényelmes út az ábrát egy térbeli alakzat vetületeként felfogni. Egy síkban maradó bizonyítás igen nehéznek látszik.
 

3. Adott a síkon 998 piros pont, semelyik három nincs egy egyenesen. Ezekhez úgy jelölünk ki kék pontokat, hogy minden olyan háromszög belsejében, amelynek csúcsai piros pontok, legyen kék pont. Melyik az a k pozitív egész szám, amelyre teljesül, hogy k kék pont felhasználásával ezt mindig meg lehet tenni, de van a piros pontoknak olyan elhelyezése, aminél k-1 pont nem elég?
 

Megoldás. Megmutatjuk, hogy a keresett szám 1991; általában n piros pont esetén, ahol n≥3, 2n-5  kék pontra szükség lehet, többre nem.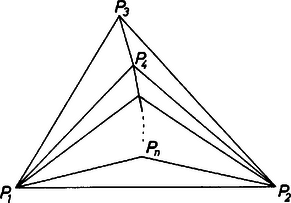
 
 

3. ábra
 
Először olyan Pi, i=1,2,...,n pontrendszert adunk meg, amelyikhez legalább 2n-5 kék pontra van szükség. Egy P1P2P3 háromszögbe rajzoljunk például egy P3-ból induló, a P1P2 oldal egy belső pontjáig menő körívet, és ennek a belsejében jelöljük ki sorra a további n-3 pontot (3. ábra.) Ekkor a P1PiPi+1, P2PiPi+1 (3≤i≤n-1) és a P1P2Pn háromszögek közül semelyik kettőnek sincs közös belső pontja, tehát mindegyik belsejében kell kék pontnak lennie. Így legalább
2(n-3)+1=2n-5
kék pontra van szükség.
Legyen most P1,P2,...,Pn tetszés szerinti piros pontrendszer. Eljárást adunk a kék pontok elhelyezésére. Választunk egy e egyenest, amelyik nem párhuzamos semelyik PiPj egyenessel, és egy elég kis d távolságot, például kisebbet az összes piroscsúcsú háromszög magasságainál. Ez lehetséges, mert csak véges sok pontpár és véges sok háromszög van.
Húzzunk most mindegyik Pi ponton át egy e-vel párhuzamos ei egyenest. Ekkor lesz olyan eu, amelyiknek az egyik oldalán nincs piros pont, és olyan ev, amelyiknek az eu-t nem tartalmazó oldalán nincsen.
Ezeken az egyeneseken nincs piros pont Pu-n, illetőleg Pv-n kívül, mert nincs három egy egyenesen levő piros pont, e választása szerint pedig ezeken az egyeneseken kettő sem lehet. Minden további ei egyenes metszi a PuPv szakaszt, ami a pontrendszer konvex burkának a belsejében halad.
Helyezzünk egy-egy kék pontot minden olyan Pi kezdőpontú félegyenesre Pi-től d távolságban, amelyiknek van közös pontja a konvex burok belsejével. Ezzel a feladat követelményeit teljesítettük. Egy piros csúcsú háromszög csúcsain át húzott egyenesek ugyanis különböznek az oldalegyenesektől. Így az egyik egyenes valamelyik félegyenesének van közös pontja a háromszög belsejével. Az ezen kijelölt kék pont d választása folytán a háromszög belsejében van.
Számoljuk össze a kék pontokat. Két-két kék pontot helyeztünk a konvex burok belsejében levő piros pontok közelébe, egyet-egyet a konvex burok határán levő piros pontokhoz, kivéve Pu és Pv-t, amikhez nem helyeztünk kék pontot. Jelöljük b-vel a konvex burok csúcsainak számát. A burok oldalszakaszainak belsejében nem lehet piros pont, így a burok belsejében n-b piros pont van. A kék pontok száma tehát
2(n-b)+b-2=2n-b-2≤2n-5.
Ezzel a bizonyítandó állítás második részét is beláttuk.
 

Megjegyzések: 1. Párhuzamos egyenesek helyett választhatunk egy O pontot a konvex burkon kívül úgy, hogy ne legyen rajta semelyik PiPj egyenesen se, és az ei=OPi egyeneseken helyezzük el a kék pontokat a fenti előírás szerint.
2. Könnyen látható, hogy az általános esetben is szükség van 2n-b-2 kék pontra. Ez következik, ha belátjuk, hogy bárhogyan is bontjuk a pontok konvex burkát olyan háromszögekre, amelyek közül semelyik kettőnek nincs közös belső pontja, a háromszögek száma mindig 2n-b-2. Ez akkor is igaz, ha lehet kettőnél több pont is egy egyenesen, csak nem mind.
Létezik a kívánt tulajdonságú felbontás. Egy ilyenhez juthatunk például úgy, hogy a pontrendszer konvex burkát háromszögekre bontjuk egy csúcsból induló átlókkal, majd veszünk egy-egy pontot, amelyik nem csúcsa megrajzolt háromszögnek, és összekötjük az őt tartalmazó háromszög vagy háromszögek csúcsaival. Véges számú pont esetén így véges számú lépésben kívánt tulajdonságú felbontáshoz jutunk.
Egy kívánt tulajdonságú felbontás háromszögeinek számát h-val jelölve ezekben a szögek összege h⋅180∘. Ezeknek a szögeknek a csúcsai pontrendszerünk pontjai. A konvex burok belsejében levő pontok mindegyike körül összesen 360∘ keletkezik (a felbontástól függetlenül). A konvex burok határán levő pontok körül keletkező szögek összege viszont egy b-szög szögeinek összege*, ami (b-2)⋅180∘. Így
h⋅180∘=(n-b)⋅360∘+(b-2)⋅180∘,   tehát   h=2n-b-2,
amint állítottuk.
* Ha egy sokszög oldalszakaszain további pontok vannak, és ezeket is csúcsoknak tekintjük egyenként 180° belső szöggel, akkor a szögek összegére vonatkozó formula nyilvánvalóan érvényben marad.