Cím: Lovagok és lókötők a gödeli szigeteken
Szerző(k):  Harcos Gergely 
Füzet: 1992/november, 337 - 342. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A címben szereplő fogalmak nyilván ismerősek azoknak, akik olvasták Raymond Smullyan: Mi a címe ennek a könyvnek c. könyvét (Műszaki Könyvkiadó, 1988), azoknak pedig, akik ezt elmulasztották volna eddig, melegen ajánlom. Igaza volt Martin Gardenernek, a Scientific American kritikusának, amikor a könyvről, mint a valaha írt legeredetibb, legtartalmasabb és legmulatságosabb logikai feladatgyűjteményről nyilatkozott. Az ,,igaza volt'' múlt idejű használata is helytálló, ha figyelembe vesszük, hogy azóta a könyv folytatása is megjelent A hölgy vagy a tigris? címmel (TypoTEX Kiadó‐Műszaki Könyvkiadó, 1991).
Képzeljük el, hogy egy bizonyos sziget lakói kizárólag lovagok, akik mindig igazat mondanak, és lókötők, akik mindig hazudnak. Feltesszük, hogy legalább egy lovag és legalább egy lókötő lakja a szigetet. A sziget lakói különböző klubokat alakítanak. Egy lakos több klubhoz is tartozhat, és minden klubnak van legalább egy tagja. Ha adott két nem feltétlenül különböző A és B lakos és egy tetszőleges C klub, akkor A vagy azt állítja, hogy B tagja a C klubnak, vagy azt, hogy nem tagja C-nek. Tekintsük most a következő két feltételt.
G (Gödeli feltétel): Bármelyik adott C klub esetén van olyan lakója a szigetnek, aki azt állítja, hogy ő tagja C-nek.
GG (Kétszeresen gödeli feltétel): Ha adott két tetszőleges klub, C1 és C2, akkor van két olyan lakos, A és B, hogy A azt állítja, hogy B tagja C1-nek és B azt állítja, hogy A tagja C2-nek.
Az elsőként említett könyv 239. oldalán szerepel a következő probléma (268a. feladat).
,,...amennyire én tudom, a G és a GG feltételek egyike sem következik a másikból. Be tudná bizonyítani, hogy sejtésem igaz? (Vagy esetleg cáfolni, de nagyon valószínűtlen, hogy sikerül.)''
Amikor a könyv olvasása közben ideértem, természetesen rögtön nekiláttam, hogy a kívánt bizonyítást elvégezzem, csakhogy nyomban egy másik problémával találtam szembe magam: a GG feltételben a C1 és C2 klubok, ill. az A és B lakosok egybeesése megengedett-e? Ha ui. mindegyik esetet számba vesszük, akkor a GG lényegében négy feltételt jelenthet.

 

GG0:GG ‐ megengedve, hogy C1=C2, ill. A=B legyen. GG1:GG0 ‐ azzal a megszorítással, hogy C1≠C2.
GG2:GG0 ‐ azzal a megszorítással, hogy A≠B.
GG3:GG0 ‐ azzal a megszorítással, hogy C1≠C2 és A≠B.
 

Jelen cikk fő célja, hogy a G és a GGi(i=0,1,2,3) feltételekkel egyenértékű, viszonylag áttekinthető feltételeket adjon, és ezáltal eldöntse, hogy ezen feltételek közül melyik következik a másikból. Az 5 feltétel (G és GGi) alapján legfeljebb 32 típusa létezik a szigeteknek, aszerint, hogy az egyes feltételek teljesülnek-e vagy sem. Látni fogjuk, hogy a 32 elvileg lehetséges típus közül csak 7 ,,valósulhat meg'', ezekből 6 típus bemutatható már egy-egy kétlakosú szigettel is (egy lovaggal és egy lókötővel), a fennmaradó 7. típushoz viszont már legalább három lakos szükséges (egy lovag és két lókötő) - ezzel a könyv 268c. feladatát is részben megoldjuk.
A rövidebb írásmód kedvéért használni fogjuk a formális logika ∧ (és), ∨ (vagy), ¬ (nem), ⇒ és ⇐ (következtetés), ⇔ (ekvivalencia) jeleit, továbbá a halmazelmélet jól ismert jelöléseit (∅,∈,⊆,∪,∩ stb.). S-sel jelöljük a sziget lakóinak halmazát, X-szel a lovagok, Y-nal a lókötők csoportját. Tehát S=X∪Y, ahol X∩Y=∅. Tetszőleges H⊆S esetén H¯=S-H a H (S-re vonatkozó) komplementere.
Mindenekelőtt nyilvánvaló, hogy
GG2⇒GG3⇒GG1  és  GG2⇒GG0⇒GG1,(1)
vagyis GG2 a legerősebb és GG1 a leggyengébb feltétel.
 

1. Ennek alapján elsőként tegyük fel, hogy szigetünkön ¬GG2 teljesül, azaz vannak olyan C1 és C2 klubok, hogy tetszőleges két különböző A és B lakos esetén A azt állítja, hogy B nem tagja C1-nek vagy B azt állítja, hogy A nem tagja C2-nek, amit így jelölünk A: ,,B∉C1'' vagy B: ,,A∉C2''.
 

1.1. eset, amikor C1-ben is és C2-ben is van lovag. Ekkor tetszőleges C1-beli x1 és C2-beli x2 lovag esetén x1: ,,x2∈C2'' és x2: ,,x1∈C1'', vagyis x1 és x2 nem lehetnek különbözőek. Ezek szerint C1-ben és C2-ben ugyanazok a lovagok vannak, sőt C1-ben és C2-ben összesen csak 1 lovag van: legyen ez J.
 

1.1.1. eset, amikor C1-nek vagy C2-nek legalább 2 tagja van. Legyen pl. |C1|≥2, ekkor C1-ben van egy y1 lókötő. Ha x1 tetszőleges lovag, akkor x1 és y1 különbözőek, továbbá x1: ,,y1∈C1'', vagyis szükségképpen y1: ,,x1∉C2'', azaz x1∈C2. Tehát az összes lovag C2-ben van, ami azt jelenti, hogy J az egyetlen lovag a szigeten. Természetesen ugyanez áll |C2|≥2 esetén is. Legyenek most y1∈C1¯ és y2∈C2¯ tetszőleges szigetlakók (ha ilyenek egyáltalán vannak). Ekkor y1 és y2 lókötők, hiszen a sziget egyetlen lovagja (J) tagja C1-nek is és C2-nek is. Tehát y1: ,,y2∈C2'' és y2: ,,y1∈C1'', vagyis y1=y2, amiből következik, hogy C1¯=C2¯={K}, ahol K lókötő. Ha y1 vagy y2 nem létezik, akkor C1¯ vagy C2¯ üres, és így C1=S vagy C2=S. Ezek szerint ebben az esetben szükséges, hogy teljesüljön az alábbi két feltétel valamelyike.
 

F1: A sziget lakói klubot alkotnak. A szigeten egyetlen lovag él.
 

F2: Van olyan klubja a szigetnek, amely e lókötő kivételével mindenkit tartalmaz. A szigeten egyetlen lovag él.
 

Az is könnyen látható, hogy F1 vagy F2 teljesülése esetén a szigeten ¬GG2. Ha ui. F1 fennáll, akkor legyen a GG2 feltételben C1=S és C2=S. Ezzel tetszőleges A és B lakosok esetén ha A: ,,B∈C1'' és B: ,,A∈C2'', akkor A és B lovagok, vagyis A=B. Ha pedig F2 teljesül, akkor legyen C1 és C2 a feltételben szereplő {K}¯ klub, ahol K lókötő. Ezzel tetszőleges A,B∈{K}¯ mellett ha A: ,,B∈C1'' és B: ,,A∈C2'', akkor B∈C1 és A∈C2 alapján A és B lovagok; de összesen csak egy lovag van a szigeten, vagyis A=B. Ha pedig pl. B=K, akkor A: ,,K∈C1'' és K: ,,A∈C2'' esetén A∉C2 (hiszen K lókötő), azaz A=K,A=B.
 

1.1.2. eset, amikor C1 és C2 is csak 1 tagot számlál. Mivel J tagja C1-nek is és C2-nek is, ezért C1={J}=C2. Legyenek most y1 és y2 tetszőleges lókötők. Ekkor y1∉C1 és y2∉C2, azaz y1: ,,y2∈C2'' és y2: ,,y1∈C1'', vagyis y1=y2, amiből |Y|=1 következik. Így ebben az esetben szükséges az alábbi feltétel.
 

F3: Van olyan klubja a szigetnek, amelynek tagságát egyetlent lovag alkotja. A szigeten egyetlen lókötő él.
Az F3 feltétel elégséges is, azaz F3⇒¬GG2. Legyen ui. C1 és C2 a feltételben szereplő {J} klub, ahol J lovag. Ezzel tetszőleges A,B∈{J}¯ mellett ha A: ,,B∈C1'' és B: ,,A∈C2'', akkor B∉C1 és A∉C2 alapján A és B lókötők; de összesen csak egy lókötő van a szigeten, vagyis A=B. Ha pedig pl. B=J, akkor A: ,,J∈C1'' és J: ,,A∈C2'' esetén A∈C2 (hiszen J lovag), azaz A=J,A=B.
⋆

Kis kitérő következik. Érdemes összehasonlítanunk az F2 és F3, feltételeket, ill. az F2⇒¬GG2 és F3⇒¬GG2 relációk bizonyítását; ezek bizonyos értelemben egymás duálisának tekinthetők. A szép szimmetriát meg is tudjuk magyarázni, ha bevezetünk egy új fogalmat.
Tegyük fel, hogy S szigetünkön mindenkinek van személyi igazolványa, amely tartalmazza, hogy az illető lovag-e vagy lókötő, továbbá minden klubhoz tartozik egy rovat, ami azt jelzi, hogy az illető annak a klubnak tagja-e vagy sem. (Az adatok hitelességét szavatolja az a tény, hogy az igazolványt kizárólag lovag hivatalnokok tölthetik ki). Mármost képzeljük el, hogy egy teliholdas éjszakán mindenkinek ellopjuk a személyi igazolványát, és pontosan az ellenkezőjére változtatjuk benne az adatokat. Varázslatunk annyira hatásos, hogy a lovagok valóban lókötőkké, a lókötők valóban lovagokká válnak. Ezzel lényegében egy új, S' szigetet hoztunk létre, új klubokkal. Az S' szigetet - az őt létrehozó f:S→S' kölcsönösen egyértelmű megfeleltetéssel - az S duálisának hívjuk. (Az f:S→S' írásmód arra utal, hogy az f az S minden lakójához, ill. klubjához az S' egy-egy lakóját, ill. klubját rendeli.) Az f két lényeges tulajdonsága - amely lényegében már meghatározza őt - az ,,igazmondás'' és a ,,klubtagság-váltás''. Most már azt is nyugodtan elképzelhetjük, hogy az S' sziget a Föld másik oldalán van, mint az S. Az is látható, hogy az S' duálisa lényegében 1 az eredeti S sziget. Számunkra különösen fontos a következő észrevétel (az S-beli X lakos, ill. C klub f-képét X'-vel, ill. C'-vel jelöljük):
Ha A és B az S lakosai és C az S klubja, akkor A: ,,B∈C''⇔A': ,,B'∈C'''. Ez ui. azt jelenti, hogy egy szigeten és a duálisán a G és a GGi(i=0,1,2,3) feltételek közül ugyanazok teljesülnek. Most már érthető, hogy F2-t és F3-t miért tekintettük egymás duálisának: S-en F2 pontosan akkor igaz, ha S'-n F3 fennáll, és fordítva. F1 duálisa például így néz ki:
 

F'1: Az üres halmaz klub. A szigeten egyetlen lókötő él.
Ez a feltétel azért maradt ki (és fog kimaradni) a többi közül, mert kizártuk azt a szemlélettel ellenkező lehetőséget, hogy egy klubnak egyetlen tagja se legyen.
⋆

A kitérőt lezárva tovább boncolgatjuk a ¬GG2 feltételt.
 

1.2. eset, amikor C1 és C2 valamelyike ‐ mondjuk C1 ‐ csupa lókötőből áll. Ha A∈C2¯ és y∈C1, akkor y lókötő, tehát y: ,,A∈C2'', vagyis y≠A esetén, ¬GG2 miatt, A: ,,y∉C1'', azaz A lókötő. Azt kaptuk, hogy y=A vagy A lókötő, vagyis A mindenképpen lókötő. Így C2¯ csupa lókötőből áll, más szóval az összes lovag C2-ben van. Legyen most x tetszőleges lovag, ekkor x∉C1. Tegyük fel, hogy C2-ben van y lókötő. Ekkor x≠y, továbbá x: ,,y∈C2'' és y: ,,x∈C1'', ami ellentmondás. Tehát C2-ben nincs lókötő: C2 éppen a lovagok halmaza. Tegyük fel, hogy C1-en kívül van y1 lókötő, és jelöljön y2 tetszőleges C1-beli klubtagot: ekkor y2 is lókötő (C1⊆Y miatt), és különbözik y1-től. Nyilván y2∉C2, tehát y1: ,,y2∈C2'' és y2: ,,y1∈C1'', ami ismét ellentmondás. Ezek szerint az összes lókötő C1-ben van, de C1 minden tagja lókötő, tehát C1 éppen a lókötők halmaza. Mindezek alapján teljesül, hogy
 

F4: A lovagok klubot alkotnak. A lókötők klubot alkotnak.
A feltétel elégséges is ¬GG2-höz. Ha ui. fennáll F4, akkor a GG2 feltételben válasszuk C1-et X-nek, C2-t Y-nak. Most tetszőleges A és B szigetlakók esetén A: ,,B∈C1'' (⇔ A: ,,B lovag'') és B: ,,A∈C2'' (⇔B: ,,A lókötő'') egyszerre nem lehetséges.
 

(Megjegyzések: 1. Az F4 duálisa önmaga.
2. Az F4⇒¬GG2 reláció kontraponált, vele ekvivalens, GG2⇒¬F4 változatát Smullyan könyvében is megtalálhatjuk ‐ 238. oldal, 267b. feladat.)
 

Az eddigieket összefoglalva:
¬GG2⇔F1∨F2∨F3∨F4,  azaz  GG1⇔¬F1∧¬F2∧¬F3∧¬F4.

Ezen a ponton mindenki fellélegezhet: a nehezén - a GG2 vizsgálatán - túl vagyunk.
 

2. Tegyük fel ezután, hogy szigetünkön nem csak ¬GG2, hanem ¬GG3 is teljesül, azaz vannak olyan különböző C1 és C2 klubok, hogy tetszőleges két különböző A és B lakos esetén A: ,,B∉C1'' vagy B: ,,A∉C2''.
2.1. eset, amikor C1-ben is és C2-ben is van lovag. Ekkor - a ¬GG2 vizsgálata során kapott eredmények szerint -

C1=SvagyC2=S,vagy(2)C1¯=C2¯(={K},aholKvalamelyik lókötő),  vagyC1=C2(={J},aholJvalamelyik lovag).

Mivel feltételeink szerint most C1≠C2, ezért C1¯≠C2¯ is, tehát (2) biztosan teljesül. Legyen C1=S≠C2. Az is igaz továbbá, hogy J, a sziget egyetlen lovagja, tagja C2-nek is. Tehát szükséges az alábbi.
 

F1*: A sziget lakói klubot alkotnak. Ezen a klubon kívül van még legalább egy olyan klub, a melynek tagja a sziget egyetlen lovagja.
Az F1* feltétel elégséges is (¬GG3 teljesüléséhez). Legyen ui. J a sziget egyetlen lovagja, C1=S és C2≠S klubok, ahol J tagja C2-nek. Legyenek A és B olyan lakosok, hogy A: ,,B∈C1'' és B: ,,A∈C2''. Ekkor B∈C1 miatt A lovag: A=J. Így B állítása is igaz, mert J∈C2 valóban fennáll, tehát B is lovag, B=J=A. (Jegyezzük meg, hogy F1*⇒F1.)
 

2.2. eset, amikor C1 és C2 valamelyike - mondjuk C1 - csupa lókötőből áll. Ekkor az 1.2. eset eredményei alapján fennáll az F4 feltétel, ami elégséges is. (Az F4⇒¬GG2 bizonyítása azért alkalmas F4⇒¬GG3 igazolására is, mert C1-et X-nek, C2-t Y-nak választottuk, ezek pedig különbözőek.)
 

Összefoglalva:
¬GG3⇔F1*∨F4,  azaz  GG3⇔¬F1*∧¬F4.

3. Tegyük fel most, hogy szigetünkön ¬GG0 is teljesül, azaz vannak olyan C1 és C2 klubok, hogy tetszőleges A és B lakosok esetén A: ,,B∉C1'' vagy B: ,,A∉C2''.
 

3.1. eset, amikor C1-ben van x1 és C2-ben van x2 lovag. Ezekkel x1: ,,x2∈C2'' és x2: ,,x1∈C1'', ami ellentmondás.
 

3.2. eset, amikor C1 és C2 valamelyike ‐ mondjuk C1 ‐ csupa lókötőből áll. Ilyenkor az 1.2. esetbeli gondolatmenettel adódik, hogy fennáll az F4 feltétel, ami elégséges is. (Az F4⇒¬GG2 bizonyítása alkalmas F4⇒¬GG0 igazolására is, hiszen ott nem használtuk ki A és B különböző voltát.)
Összefoglalva:
¬GG0⇔F4,  vagyis  GG0⇔¬F4.

4. Végül tegyük fel, hogy a szigeten ¬GG1 is teljesül, azaz vannak olyan különböző C1 és C2 klubok, hogy tetszőleges A és B lakosok esetén A: ,,B∉C1'' vagy B: ,,A∉C2''. Ekkor a ¬GG0-ra vonatkozó eredmény szerint teljesül F4, ami elégséges is, hiszen ismét megfelel C1=X,C2=Y. Tehát
GG1⇔¬F4,
így az előbbi eredményünk szerint
GG0⇔GG1.
A GG0 és a GG1 feltételt együttesen jelölhetjük GG01-gyel. Vagyis

GG2⇒GG3⇒GG01.(3)



5. Most pedig lássuk az egyszeresen gödeli G feltételt. Tegyük fel, hogy szigetünkön ¬G, azaz van olyan C klub, hogy tetszőleges A szigetlakó esetén A: ,,A∉C''. Ekkor A∉C⇔A lovag, azaz A∈C⇔A lókötő, tehát C éppen a lókötők halmaza. Igaz ezért, hogy
 

F: A lókötők klubot alkotnak.
A gondolatmenetet megfordítva a C=Y választással adódik, hogy az F feltétel elégséges is. Így
¬G⇔F,  azaz  G⇔¬F.

(Ez az eredmény szerepel Smullyan könyvében a 232-233 oldalakon, a 264b. feladat második részeként.) Vegyük észre, hogy F4⇒F, vagyis G⇔¬F⇒¬F4⇔GG01, tehát (3) felhasználásával

GG2⇒GG3⇒GG01⇐G.(4)



A dolgozat elején idéztük, hogy Smullyan igen valószínűtlennek találja, hogy a G⇒GG következtetést bárki is igazolni tudja. Ennek alapján feltételezhető, hogy könyvének írásakor a GG feltétel esetében a GG2 vagy a GG3 feltételre gondolt. Mint később kiderül, a (4) reláción kívül több következtetést nem tudunk felállítani a G és a GGi feltételek között, tehát a GG2 és a GG3 feltétel között sem tudunk majd dönteni. Józan paraszti ésszel gondolkodva azonban valószínű, hogy a GG3 feltétel az ,,igazi''.
A (4) miatt a szigeteknek 7 típusát különíthetjük el aszerint, hogy a G és a GGi feltételek közül melyik teljesül. A típusokat az áttekinthetőség kedvéért táblázatba rendezve soroljuk fel. Ha mindazokat a szigeteket, amelyeken csak egy lovag és csak egy lókötő él, besoroljuk az 1-7 típusok valamelyikébe, akkor azt találjuk, hogy a 6-os kivételével mindegyik típus bemutatható egy-egy két lakosú szigettel. A 6-os típusba csak olyan sziget tartozhat, amelyen egyetlenegy lovag él. Három lakosú, 6-os típusú sziget már létezik; ezen 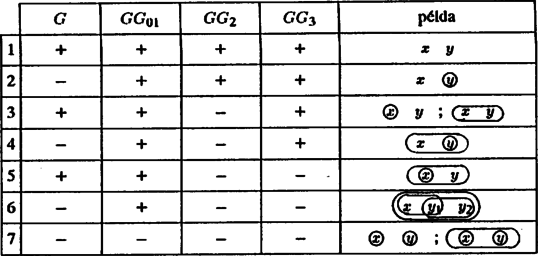|X|=1,|Y|=2.
 
 
1Két szigetet akkor tekintünk lényegében azonosnak, ha az egyik sziget lakosait és klubjait ,,át tudjuk nevezni'' úgy, hogy a másik sziget lakóihoz és klubjaihoz jussunk.