Cím: Szélsőérték feladatokkal kapcsolatos problémák (A 2660. gyakorlat ürügyén)
Szerző(k):  Surányi János 
Füzet: 1992/május, 193 - 196. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A címben említett gyakorlat így szólt: Az AB átmérőjű kör tetszőleges pontja P. A P középpontú, PA sugarú kör az AB egyenest C-ben metszi. Mikor lesz az APC háromszög területe a legnagyobb? A közölt elemi megoldás* a mértani és számtani közép közti egyenlőtlenséget használja fel. A maximumot a 3r alapú háromszög szolgáltatja.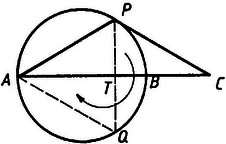

 
 

1. ábra
 

A feladat így kissé erőltetettnek tűnik, pedig egy elég természetes kérdéshez jutunk, ha 180°-kal elforgatjuk a P pont AB-n levő T merőleges vetülete körül a háromszög CPT felét (1. ábra). Ekkor ugyanis a C pont A-ba kerül, P pedig az AB-re vonatkozó Q tükörképébe, ami a körön van. Ahhoz a kérdéshez jutottunk tehát, hogy adott körbe írt egyenlő szárú háromszögek közül melyiknek a legnagyobb a területe. A talált megoldás könnyen láthatóan azt adja, hogy a szabályos háromszögé.
Vizsgálhatjuk általánosabban azt a kérdést, hogy az adott körbe írt összes háromszögek közül melyiknek legnagyobb a területe. Ha válaszul most is a szabályos háromszöget kapjuk, (tehát egyenlő szárút), akkor ez az előbbi, speciálisabb problémának is megoldása.
Kényelmes lesz a továbbiakban sokszögek területét ugyanúgy jelölni, mint magát a sokszöget. Ez nem fog félreértésre okot adni.
 
 

2. ábra
 

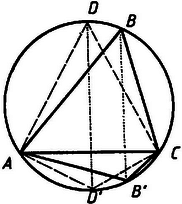
2. Az utolsó kérdésre a múlt században a következő meglepően egyszerű válasz született. Ha az ABC háromszögben AB≠BC, és az ABC ív felezőpontja D, akkor
ADC>ABC,
mert a közös oldalra merőleges magasságoknak ez a viszonya (2. ábra). Így minden háromszöghöz találunk nagyobb területűt, csak a szabályoshoz nem, annak kell tehát a legnagyobb területűnek lennie.
A bökkenő csak az, hogy ezzel a gondolatmenettel azt is be lehet látni, hogy 1 a legnagyobb pozitív egész szám; hiszen négyzetre emelve őket mindegyikhez egy nagyobbat kapunk, csak az 1 marad 1.
Kereshetnénk a hibás eredmény okát abban, hogy a pozitív egészek közt előfordul bármilyen számnál nagyobb, viszont háromszögeink területe mindig kisebb például a kör területénél. Ez sem oldja azonban meg a problémát.
A 2-1/n(n=1,2,...) számok mind kisebbek, mint 2, és mindegyikhez egy nagyobb pár a 2-1/n2, kivéve, ha n=1, amikor a szám párja önmaga. Gondolatmenetünk szerint tehát ezek közt a számok közt is a 2-1/1=1-nek kellene a legnagyobbnak lennie, holott ő a legkisebb.
3. Az ellenvetések természetesen jogosak, mégis az lehet az érzésünk, hogy a felvetett alapgondolatból kiindulva valahogyan el lehet jutni annak elemi geometriai úton történő bizonyításához, hogy adott körbe írt háromszögek közül a szabályos háromszög területe a legnagyobb.
Próbáljuk meg ismételten alkalmazni az eljárást. Jelöljük a csúcsokat és szögeket a szokásos módon, és válasszuk a jelölést úgy, hogy α≤β≤γ álljon fenn. Ha a háromszög nem szabályos, akkor könnyű látni, hogy
α<60∘<γ.(1)

Ha most B-t az ABC ív felezőpontjába toljuk, akkor a kerületi szögekre vonatkozó tétel szerint β változatlan marad, a másik két szög pedig 90∘-β/2-re változik.
Ha β történetesen 60∘, akkor azt kapjuk, hogy a kiindulási háromszög területe kisebb a szabályosénál. Ha β≠60∘, akkor az új háromszög szögeinek 60∘-tól való eltérését nézve a szögek
60∘+(30∘-β/2),60∘+(30∘-β/2),60∘-(60∘-β).

Bevezetjük a δ=30∘-β/2=(60∘-β)/2 jelölést. Ekkor a szögek
60∘+δ,60∘+δ,60∘-2δ.
Itt δ lehet pozitív is, negatív is aszerint, hogy β<60∘, vagy β>60∘.
Az eljárást most az egyik szár rögzítésével kell megismételnünk, tehát β szerepét az egyik 60∘+δ  nagyságú szög veszi át. Így a két egyenlő szög nagysága
90∘-(60∘+δ)/2=60∘-δ/2
lesz, tehát az újabb háromszög szögei
60∘-δ/2,60∘-δ/2,60∘+δ.
A lépések számát (1, illetőleg 2) n-nel jelölve a két eset így foglalható össze:
60∘+(-1/2)n-1δ,60∘+(-1/2)n-1δ,60∘+(-1/2)n-2δ.
Ha n valamilyen m értékére a szögek ilyen alakúak, akkor az m+1-edik lépésben az egyik 60∘+(-1/2)m-1δ=60∘+(-1/2)(m+1)-2δ nagyságú szög marad változatlan, a másik kettő pedig a következőre változik:
90∘-[60∘+(-1/2)m-1δ]/2=60∘+(-1/2)mδ=60∘+(-1/2)(m+1)-1δ.
A talált szabályosság tehát az m+1 -edik lépés után is érvényben marad, így minden lépésszám esetén fennáll.
Azt találtuk tehát, hogy ha szabályos háromszöget nem is kapunk, de a lépések számának növelésével ahhoz tetszés szerint közel kerülhetünk, a terület pedig eközben állandóan növekedik. Ez még jobban valószínűsíti a várt eredmény helyességét, de bizonyításnak még mindig nem tekinthető. Gondoljunk csak arra, hogy a 2-1/n alakú számok közt nem volt legnagyobb. Biztos-e, hogy háromszögeink közt van legnagyobb területű? Az okoskodás határátmenet képzésével teljessé tehető, de így egyszerűnek, vagy eleminek már nehezen mondható.
4. Egy egyszerű ötlettel mégis megmenthető a gondolatmenet elemi geometriai jellege. Gondoljunk arra, hogy egy lényegtelennek tűnő speciális esetben, ha β=60∘, egy lépésben eljutottunk a szabályos háromszöghöz. Nem lehet-e az általános esetet erre visszavezetni? Erre a fellépő váltakozó előjel reményt nyújt.
Valóban, ha β<60∘, tehát δ pozitív, akkor az első lépésben az (1) szerint 60∘-nál kisebb α 60∘-nál nagyobbra változik, ha meg β>60∘, akkor a 60∘-nál nagyobb γ változik 60∘-nál kisebbre.
 
 

3a ábra
 

 
 

3b ábra
 

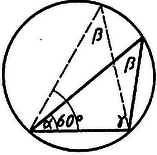
Legyünk az első lépésben kevésbé mohók, ne törekedjünk a legnagyobb növelésre B mozgatásával, hanem az első esetben csak addig növeljük a háromszög területét, míg α el nem éri a 60∘-ot, a másodikban pedig csak addig, míg γ60∘-ra nem csökken (3. ábra). Ezután megismételve az eljárást, a második lépésben már a szabályos háromszöghöz jutunk. Így az eredeti gondolat körültekintőbb alkalmazásával legfeljebb két lépésben eljutunk annak megmutatásához, hogy ha egy körbe írt háromszög nem szabályos, akkor területe kisebb, mint a szabályosé. Ezzel a kimondott állításnak valóban egyszerű geometriai bizonyításához jutottunk.
5. Az eddigiekben a körbe írt egyenlő szárú háromszögekre vonatkozó problémát egy általánosabb problémába ágyazva oldottuk meg, azonban a 2. pontban felvetett eljárás, amelyik minden a körbe írt, nem szabályos háromszöghöz egy nagyobb területű egyenlő szárút szolgáltat, azt is jelenti, hogy az általános probléma helyett elegendő azt megmutatni, hogy adott körbe írt egyenlő szárú háromszögek közül a szabályos területe a legnagyobb.
 
 

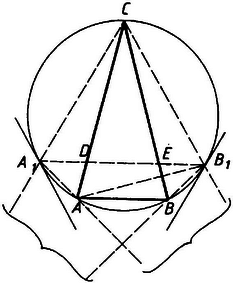4a ábra
 

Ez is megoldható elemi geometriai meggondolással. Legyen ABC egy körbe írt háromszög, amelyikre AC=BC≠AB, és A1B1C az a szabályos háromszög, amelyiknek egyik csúcsa C. Ha ACB∢<60∘, akkor jelöljük D,E-vel az A1B1 szakasz metszéspontját az AC, illetőleg a BC szárral (4a. ábra.) Ez esetben azt kell megmutatnunk, hogy
ABED<A1DC+EB1C.
Ehelyett, mindkét területhez hozzávéve A1AD+BB1E-t, azt látjuk be, hogy
A1ABB1<A1AC+BB1C.
Ehhez, a trapézt az AB1 átlóval két részre vágva, azt mutatjuk meg, hogy
ABB1<BB1C  ésA1AB1<A1AC.
Mindkét esetben a közös oldalra bocsátott magasságok közül a C-ből induló a nagyobb. Ez a következőképpen látható be. A körhöz az A1-ben húzott érintő B1C-vel párhuzamos, a B1-ben húzott pedig A1C-vel. Az A1ABB1 körív félkörnél kisebb (harmadkör), így azt mindkét egyenespár közti sáv tartalmazza. Ezért A1A a B1C oldal B1-en túli meghosszabbítását metszi, B1B pedig A1C-nek az A1-en túli meghosszabbítását, s így CA-nak is az A-n túli meghosszabbítását. Ebből állításaink következnek.
 
 

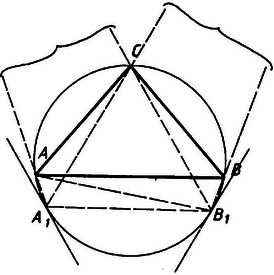4b ábra
 

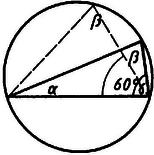
Ha ABC∢>60∘, akkor AB metszi az A1C és B1C szárat (4b. ábra). Az előbbiekhez hasonlóan most annak bizonyítására vezethetjük vissza a feladatot, hogy
AA1B1B>AA1C+B1BC,
illetőleg tovább az
AA1B1>AA1C ésAB1B>B1BC
egyenlőtlenségek bizonyítására.
Mivel az A1-ben és B1-ben húzott érintő párhuzamos a szabályos háromszög szemben levő oldalával, továbbá A a kör A1AC harmadán van, B pedig a B1BC harmadon, így az A1A egyenes B1C-t a C-n túli meghosszabbításában metszi, B1B pedig A1C-t, s így AC-t is ugyancsak a C-n túli meghosszabbításában.
Ebből következik, hogy mindkét háromszögpárnál a közös oldalra merőleges magasságok közül a C-ből húzott a kisebb. Így most is fennáll mindkét egyenlőtlenség. Ezzel beláttuk a körbe írt egyenlő szárú háromszögekre kimondott tételt.
6. Térjünk még egyszer vissza a 2. pontban elemzett okoskodásra. Egy számhalmaz minden eleméhez hozzárendeltük egy nála nem kisebb elemét, és azt mondtuk, amelyikhez önmagát rendeltük, az a legnagyobb elem. Az egyik ellenpéldában az 1 és a  2 közti xn=2-1/n számokhoz(n=1,2...) a  2-1/n2-et rendeltük hozzá. Ezzel valóban növeltünk, mert
2-1n2=2-1n+1n(1-1n)=xn+(2-xn)(xn-1).

Ebben az alakban a hozzáadandó nem csak az adott számhalmaz elemeire, hanem minden 1<x<2 számra pozitív, viszont a számhalmaz két szélén, x=1-re és x=2-re 0. Ezzel minden esetre a legnagyobb elem is fellépett, a 2, ami a 2-1/n alakú számok közt nem szerepel.
 
 

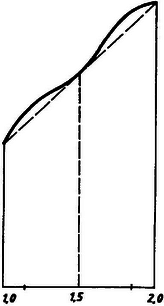5. ábra
 
Ha a fenti hozzárendelés helyett x-hez például az
x+(2-x)(x-1)(2x-3)2
értéket rendeljük hozzá, belátható, hogy 1 és 2 közti x-ekre ez is 1 és 2 közé esik (5.ábra), de most már csak az 1, 1,5 és 2 kivételével jelent növekedést. Az tehát, hogy egy ilyen nem csökkentő hozzárendelés hol növel, hol nem, inkább a hozzárendelésre jellemző, mint a halmazra, amin értelmezve van. A halmazról csak annyit mondhatunk, hogy ha van legnagyobb eleme, azt a hozzárendelés nem növelheti. Ahhoz tehát, hogy egy ilyen fajta okoskodás bizonyító erejű legyen, mindenképpen szükséges bizonyítani, hogy a halmaznak van legnagyobb eleme.
*Lásd e Lapok 41. (1991. évi) kötetének 456‐457. oldalán.