| Cím: | Az exponenciális függvények | ||
| Szerző(k): | Láng Hugó | ||
| Füzet: | 1992/február, 53 - 59. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Sok matematika könyv egymástól eltérően definiálja az exponenciális függvényeket.  1. ábra Vizsgálva az azonosságokat, beláttuk, hogy Az értelmezést ki akarjuk terjeszteni a kitevőjű hatványra a fenti azonosságok megmaradásával. Legyen pozitív egész, a fenti azonosságok alapján egyenlőségnek teljesülnie kell, azaz Ha , ez az egyenlőség akkor és csak akkor igaz, ha megállapodunk az (ha ) definícióban. Ha , az egyenlőség az utolsó tényező tetszőleges értéke mellett is teljesül, ezért -nek az helyen nem adunk helyettesítési értéket. Az egész kitevőjű hatvány fogalmához ismét a felsorolt azonosságok permanenciája révén jutunk. Ha és egész, , ha , amely akkor igaz, ha , vagyis a -tól különböző alapok esetén minden egész kitevőjű hatványt értelmezhetünk. A -nak eddig csak pozitív egész kitevőjű hatványát sikerült definiálnunk. A függvények grafikonja most is diszkrét pontok halmaza, de igen jellemző tulajdonságokkal (2. ábra). 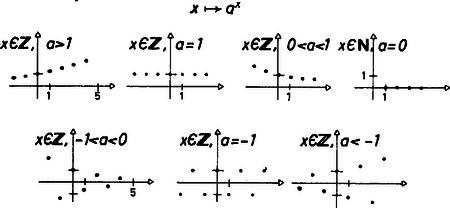 2. ábra A hatvány fogalmát racionális kitevőre ismét a felsorolt azonosságok permanenciája alapján terjesztjük ki. Ha és egész, , például hatványt -adik hatványra emeléssel könnyen vissza lehet vezetni egész kitevős hatványra, s így a célszerű definíció: . Itt azonban fellépnek már értelmezési nehézségek. Nem szoktunk negatív kitevőjű gyököket alkalmazni (bár vannak országok, ahol ezt megteszik), de ezen könnyen lehet segíteni: és , illetve és esetén miatt el lehet érni, hogy a gyökkitevő pozitív legyen. Nagyobb gond van a definíciójával, ha , páratlan és páros, mert a jobb oldalon álló kifejezésnek nincs értelme a valós számok halmazán. Másrészt , tehát valós szám. Tehát vagy el kellene fogadnunk, hogy a törtkitevő nem bővíthető, ami aligha lenne célszerű, vagy le kellene mondanunk a negatív alap racionális kitevőjű hatványainak értelmezéséről (ha a racionális kitevő nem egész). Az utóbbit szoktuk tenni. A különböző alapok esetén exponenciális függvényeink a legbővebb értelmezési tartományon a következő grafikonokat adják (3.ábra): 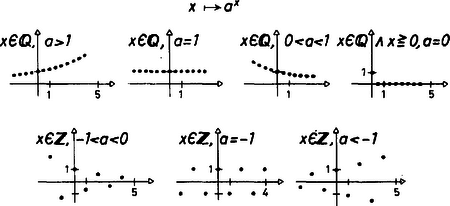 3. ábra Részletesen vizsgálva függvényeinket, megállapíthatjuk, hogy közülük szigorúan monoton nő , ha , szigorúan monoton fogy, ha , konstans értékű, ha vagy , nem monoton, de kölcsönösen egyértelmű, ha vagy , nem monoton s nem is kölcsönösen egyértelmű, ha . Az irracionális kitevőjű hatvány célszerű jelentését keresve az előbbi azonosságok alkalmazásával nem tudjuk a feladatot racionális kitevőjű hatványra visszavezetni. (ha racionális, irracionális), ( racionális esetén vagy , és akkor érdektelen, vagy irracionális). Itt a monotonitás megmaradását érdemes megkövetelnünk. Meg lehet mutatni, hogy ekkor az azonosságok is megmaradnak. Ha irracionális szám, tekintsük a racionális számokból álló számsorozatokat, akkor esetén az sorozat konvergens, és legyen . (Meg kell követelnünk, hogy ne lehessen negatív, hiszen negatív alapnak csak egész kitevőjű hatványait sikerült értelmeznünk, s a sorozat nem állhat csupa egész számból). esetén nincs probléma, ha elemei pozitív számok, tehát a pozitív irracionális kitevőjű hatványait is értelmezni tudjuk. Sőt, lehetővé válik határértékkel való definíciója is. (Ez azonban az irodalomban eltérő eredményekhez is vezet. Ha t.i. ( pozitív racionális) sorozatot választjuk, ennek határértéke . Viszont Összefoglalva tehát: minden valós kitevőre értelmeztük az függvényt, ha ekkor a függvény szigorúan monoton nő, ekkor a függvény konstans, ekkor a függvény szigorúan monoton csökken, minden pozitív valós kitevőre (és kitevőre) értelmeztük esetén, a függvényérték pozitív kitevőre ( kitevőre az értéke ); egész kitevőkre értelmeztük az függvényt, ha ekkor a függvény kölcsönösen egyértelmű hozzárendelés, a grafikon pontjai diszkrét pontok, a pontsor "tartója'' páros kitevőre páratlan kitevőre grafikonja; , ekkor a függvény páros helyeken , páratlan helyeken értéket vesz fel. A különböző alapú exponenciális függvényeket az alaptól függően legbővebb értelmezési tartományukon a .ábra szemlélteti. 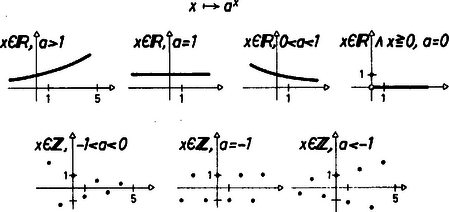 4. ábra Lássunk néhány példát: Érdemes szemügyre vennünk az függvényt a legbővebb értelmezési tartományán. A gondot az értelmezési tartomány okozza: esetén a kitevő bármely valós szám lehet, esetén csak egész szám. pontban nincs helyettesítési érték, viszont van jobb oldali határérték, ami . (Ezért célszerű -t az függvény jobb oldali határértékével definiálni.) Vizsgáljuk meg a függvény menetét. A pozitív számok halmazán ‐ némileg meglepő módon ‐ a függvény előbb monoton fogy, majd helyi minimum után végig szigorúan nő: helyi minimumát felveszi, ha (5.ábra). 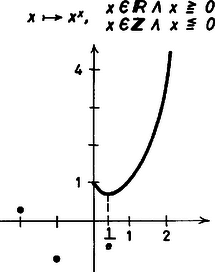 5. ábra Mindenesetre, ha , bár ezen az intervallumon nincs kölcsönös egyértelműség. Viszont vagy esetén már van, bár a függvény csak esetén szigorú monoton növő. (Szép példa arra, hogy a szigorú monotonitás a kölcsönösen egyértelműségnek elégséges, de nem szükséges feltétele.) Némileg másképpen alakul a helyzet, ha a függvényt elemezzük a lehető legbővebb értelmezési tartományán. Ez: az -nél nagyobb valós számok, és az -nél kisebb egész számok. Ha , azaz , akkor a kitevő ; -nél nagyobb számok -nál nagyobb hatványai mind nagyobbak -nél. Ha , azaz , akkor , a függvény értéke . Ha , azaz , akkor ; és közötti számok és közé eső hatványai pozitívak és kisebbek -nél. Ha , azaz , a kitevő , a függvény értéke . Ha , azaz , csak akkor van értelmezve, ha egész szám. Lássunk további példákat. 2. Oldjuk meg az egyenletet. Ha , azaz , a kitevő kell legyen, ez a megengedett kiindulási hal- mazon . Ha , azaz , a kitevő a kiindulási halmaz tetszőleges eleme, de mert az egyelemű, . Ha , azaz , a kitevő kellene, hogy legyen, de a kiindulási halmaznak nincs ilyen eleme. Ha , azaz , a kitevő pozitív kellene legyen, tehát nincs megoldás. Ha , azaz , a kitevő egész és értékű, a kiindulási hal- mazon nincs megoldás. Ha , azaz , a kitevő páros egész, tehát . Ha , azaz , a kitevő egész és értékű, a kitevőnek a kiindulási halmazon nincs helye. Végül is az egyenlet megoldásai: és . 3. Oldjuk meg az egyenletet. Ha az alap pozitív és , azaz , illetve esetben a kitevők tetszőleges, egymással egyező valós számok: , azaz , tehát . Ha az alap , azaz , a függvény konstans, az egyenlőség a kitevőktől füg- getlenül teljesül, . Ha az alap , tehát , a kitevő tetszőleges pozitív szám, esetén és , tehát Ha vagy , azaz vagy , a kitevő csak egész lehet, az ilyen alapú exponenciális függvény egyértelmű, tehát az egyenlőség teljesüléséhez a kitevőknek meg kell egyezni: ezen a kiindulási halmazon egy ilyen gyök van: . Ha , azaz , a kitevőknek egészeknek kell lenni és egyező párosságúnak, mivel ez teljesül, megoldás. Az egyenlet gyökei a valós számok halmazán: . Igazságuk behelyettesítéssel könnyen ellenőrizhető. 4. Oldjuk meg az egyenlőtlenséget: . Ha az alap nagyobb -nél, akkor Ilyen alap esetén az egyenlőtlenség akkor teljesül, ha a kitevő negatív: , azaz, ha . A megoldás első részhalmaza a két halmaz közös része: Ha , az egyenlőtlenség akkor igaz, ha a kitevő értéke pozitív. Tehát a kiindulási halmaz: Ha az alap értéke , az egyenlőtlenség teljesül, ha a kitevő pozitív valós szám. , ha vagy . Közülük a kitevő akkor pozitív, ha , tehát . Ha az alap értéke és között van, az egyenlőtlenség értelmezve van, ha a kitevő egész, és teljesül is, ha a kitevő pozitív egész, vagy negatív páratlan egész. A kiindulási halmaz a kettő közös része: A kitevőben szereplő kifejezés: , pozitív értékű, ha vagy , vagyis a kitevő a kiindulási halmaznak részhalmazán pozitív. Mivel ez az intervallum a másodfokú függvény szigorúan monoton csökkenő részén helyezkedik el, a kitevő értékkészletére , tehát ha a kitevő pozitív egész, értéke csak vagy lehet. Az egyenletnek -be eső gyöke , az egyenletnek -be eső gyöke , s mivel feltétellel a kitevő nem lesz negatív páratlan, tehát Ha , az egyenlőtlenség értelmezve van, ha a kitevő értéke egész szám, és teljesül, ha a kitevő páratlan. , tehát Ezeket az polinomba helyettesítve a helyettesítési érték , tehát nem egész szám. Ezen a részhalmazon a megoldási halmaz üres. Ha , az egyenlőtlenségben szereplő kifejezés értelmezve van, ha a kitevő helyettesítési értéke egész szám, és az egyenlőtlenség teljesül, ha a kitevő negatív egész, vagy pozitív páratlan egész. Mivel a kitevőt adó függvény szigorúan monoton csökkenő szakaszára esik, s a kitevőnek ezen az intervallumon a negatív értékei és között vannak, a kitevő lehetséges értékei és . A kitevő ezeket az értékeket rendre a és helyeken veszi fel. A kitevő pozi- tív a intervallumon. Itt a kitevő szigorúan monoton fogy, érték- készlete Így a kitevő akkor pozitív páratlan egész, ha értéke . Ezt a kitevő az helyen veszi fel.Te- hát Összefoglalva a feladat megoldásai: |