Cím:	1991. A 22. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Honyek Gyula ,  Szép Jenő
Füzet:	1991/november, 401 - 410. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Elméleti feladatok   1. feladat. Az 1. ábrán egy $R$ sugarú szilárd homogén golyó látható. Mielőtt leesne a talajra, tömegközéppontja nyugalomban van, azonban a golyó ${\omega }_0$ szögsebességgel forog egy tömegközéppontján átmenő vízszintes tengely körül. A golyó legalsó pontja $h$ magasságban van a talaj felett. 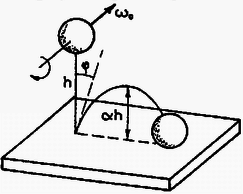    1. ábra   Mikor elengedjük, a golyó a gravitáció hatására leesik, és eredeti magasságának adott $\alpha$-szorosára pattan vissza. A golyó és a talaj olyan anyagból vannak, hogy az ütközés során fellépő alakváltozás elhanyagolható. A golyó és a talaj közti csúszási súrlódási együttható ${\mu }_k$ adott. Tegyük fel, hogy az ütközés ideje nagyon kicsi, de véges, és a golyó légüres térben esik. Jelölje m a golyó tömegét, $g$ a gravitációs gyorsulást. A golyó tehetetlenségi nyomatéka a tömegközépponton átmenő tengelyre: $\Theta =2m{R}^2/5$. 1. Először vizsgáljuk azt az esetet, amikor a golyó az ütközés teljes ideje alatt csúszik. Határozd meg: a) A $\phi$ visszapattanási szög tangensét! b) A tömegközéppont által megtett vízszintes távolságot az első és a második ütközés között! c) ${\omega }_0$ legkisebb lehetséges értékét!   2. Tegyük fel most, hogy a csúszás befejeződik az ütközési időtartam vége előtt. Válaszolj ismét az a) és b) kérdésekre!   3. Ábrázold szabadkézi rajzban $\text{tg}\phi$ függését ${\omega }_0$-tól a fenti két esetben!   Megoldás. A golyó $v_0=\sqrt[]{2gh}$ sebességgel érkezik a talajra, majd visszapattan. Ekkor függőleges sebességkomponense $v_y=\sqrt[]{2g\alpha h}=c{v}_0$, ahol $c=\sqrt[]{\alpha }$ az ütközési szám, míg a vízszintes sebességkomponens legyen 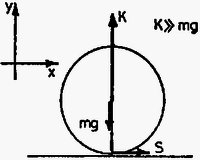$v_x$.     2. ábra   A 2. ábrán látható erők segítségével írjuk fel a lendület és a perdület megváltozását az ütközés ideje alatt: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \Delta I_x={\int }_{t_1}^{t_2}S\left(t\right)dt=m{v}_x\mathrm{,}}\hfill \\ \hfill {\displaystyle \Delta I_y={\int }_{t_1}^{t_2}K\left(t\right)dt=m{v}_0+m{v}_y=m\left(1+c\right)\sqrt[]{2gh}\mathrm{,}}\hfill \\ \hfill {\displaystyle \Delta N={\int }_{t_1}^{t_2}RS\left(t\right)dt=R{\int }_{t_1}^{t_2}S\left(t\right)dt=\Theta \left({\omega }_0-{\omega }_1\right)\mathrm{,}}\hfill \end{array}}$ ahol ${\omega }_1$ az ütközés utáni szögsebesség, míg $t_1$ és $t_2$ az ütközés kezdő-, illetve végső pillanata. Két eset lehetséges: 1. A teljes ütközési idő alatt csúszik a golyó. 2. Egy bizonyos $t\in \left(t_1\mathrm{,}{t}_2\right)$ időpontban a golyó talajjal érintkező pontjának sebessége nullává válik; ettől kezdve megszűnik a csúszás, nem lép fel súrlódási erő, a golyó tiszta gördüléssel halad.   1. eset. Ekkor az ütközés minden időpillanatában így adható meg a súrlódási erő: $\begin{array}{c}{\displaystyle S\left(t\right)={\mu }_{k}K\left(t\right)\mathrm{,}}\end{array}$ amit a fenti összefüggésekbe behelyettesítve a következő egyenletekhez jutunk: $\begin{array}{c}{\displaystyle \Delta I_x={\mu }_k\underset{t_1}{\overset{t_2}{\int }}K\left(t\right)dt={\mu }_k\cdot \Delta I_y={\mu }_{k}m\left(1+c\right)\sqrt[]{2gh}=m{v}_x\mathrm{,}}\end{array}$ és $\begin{array}{c}{\displaystyle \Delta N=R{\mu }_k\underset{t_1}{\overset{t_2}{\int }}K\left(t\right)dt=R{\mu }_{k}m\left(1+c\right)\sqrt[]{2gh}=\Theta \left({\omega }_0-{\omega }_1\right)\mathrm{,}}\end{array}$ melyekből a $v_x$ vízszintes sebességkomponens és az ${\omega }_1$ végső szögsebesség kiszámítható: ${\displaystyle \begin{array}{c}\hfill {\displaystyle v_x={\mu }_k\left(1+c\right)\sqrt[]{2gh}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\omega }_1={\omega }_0-\frac{{\mu }_{k}mR\left(1+c\right)}{\Theta }\cdot \sqrt[]{2gh}\mathrm{.}}\hfill \end{array}}$ Ennek a megoldásnak a feltétele: ${\omega }_{1}R>v_x$. Behelyettesítve ${\omega }_1$ és $v_x$ értékét, a kezdeti szögsebességre a következő feltételnek kell teljesülnie: $\begin{array}{c}{\displaystyle {\omega }_0>\frac{{\mu }_k\sqrt[]{2gh}\left(1+c\right)}{R}\left[\frac{m{R}^2}{\Theta }+1\right]\mathrm{.}}\end{array}$   2. eset. Ekkor $t_1$ és $t_2$ között valamikor tiszta gördülés indul meg, melynek kinematikai feltétele: ${\omega }_{1}R=v_x$. Ennek segítségével $v_x$ és ${\omega }_1$ a következő egyszerű alakra hozható: $\begin{array}{c}{\displaystyle v_x=\frac{\Theta {\omega }_{0}R}{m{R}^2+\Theta }=\frac{2}{7}{\omega }_{0}R\mathrm{.}}\end{array}$ és $\begin{array}{c}{\displaystyle {\omega }_1=\frac{\Theta {\omega }_0}{m{R}^2+\Theta }=\frac{2}{7}{\omega }_0\mathrm{,}}\end{array}$ vagyis ezek a mennyiségek ebben az esetben csak a kezdeti ${\omega }_0$-tól függnek, a $h$ indítási magasságtól nem.   A visszapattanási szög tangensének kiszámítása   1. eset. A kívánt tangens érték a visszapattanási sebesség komponenseinek hányadosaként állítható elő: $\begin{array}{c}{\displaystyle \text{tg}\phi =\frac{v_x}{v_y}=\frac{{\mu }_k\left(1+c\right)\sqrt[]{2gh}}{c\sqrt[]{2gh}}={\mu }_k\frac{\left(1+c\right)}{c}\mathrm{,}}\end{array}$ azaz a $\phi$ szög ${\omega }_0$-tól is, $h$-tól is független.   2. eset. Az előzőhöz hasonló módon eljárva: 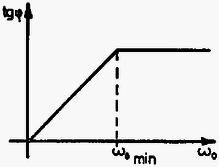$\begin{array}{c}{\displaystyle \text{tg}\phi =\frac{v_x}{v_y}=\frac{\Theta {\omega }_{0}R}{\Theta +m{R}^3}\cdot \frac{1}{c\sqrt[]{2gh}}=\frac{2{\omega }_{0}R}{7c\sqrt[]{2gh}}\mathrm{,}}\end{array}$ azaz $\text{tg}\phi$ fordítottan arányos $\sqrt[]{h}$-val, míg ${\omega }_0$-lal egyenesen arányos.     3. ábra   A 3. ábrán grafikusan ábrázoltuk $\text{tg}\phi$ függését ${\omega }_0$-tól mindkét esetet figyelembe véve. Az eddigiek alapján ${\omega }_0$ minimális értéke könnyen meghatározható: $\begin{array}{c}{\displaystyle {\omega }_{0_{min}}=\frac{{\mu }_k\left(1+c\right)\sqrt[]{2gh}}{R}\left[\frac{m{R}^2}{R}+1\right]=\frac{7{\mu }_k\left(1+c\right)\sqrt[]{2gh}}{2R}\mathrm{.}}\end{array}$   A második ütközési pont távolságának kiszámítása   1. eset. A golyó emelkedési és esési ideje: $\begin{array}{c}{\displaystyle t_e=2\frac{v_y}{g}=\frac{2c\sqrt[]{2gh}}{g}=2c\sqrt[]{\frac{2h}{g}}\mathrm{,}}\end{array}$ így a kívánt távolság: $\begin{array}{c}{\displaystyle d_1=v_x{t}_e={\mu }_k\left(1+c\right)\sqrt[]{2gh}\cdot 2c\sqrt[]{\frac{2h}{g}}=4{\mu }_k\left(1+c\right)c\cdot h\mathrm{,}}\end{array}$ ami ${\omega }_0$-tól nem függ.   2. eset. A $t_e$ emelkedési és esési idő ebben az esetben is ugyanakkora, mig $v_x$ kifejezése eltérő. Így a kívánt távolság: $\begin{array}{c}{\displaystyle d_2=v_x{t}_e=\frac{\Theta {\omega }_{0}R}{m{R}^2+\Theta }\cdot 2c\sqrt[]{\frac{2h}{g}}=\frac{4}{7}c\sqrt[]{\frac{2h}{g}}R{\omega }_0\mathrm{.}}\end{array}$ Ebben az esetben a második ütközési pont távolsága ${\omega }_0$-val egyenesen arányos.   2. feladat. Egy négyzet alakú hurkon, amelynek minden oldala $L$ hosszúságú, nagyszámú elhanyagolható méretű, egyenként $q$ töltésű golyó mozog nagyon gyorsan, $u$ sebességgel, miközben a köztük lévő távolság minden esetben ,,$a$'' a hurokhoz rögzített koordináta-rendszerből nézve. A golyók úgy vannak a hurokra felfűzve, mint a gyöngyök egy nyakláncra, továbbá $L$ sokkal nagyobb, mint "$a$'' (lásd a 4. ábrát). A hurkot alkotó elektromosan nem vezető huzal olyan homogén töltéssűrűséggel rendelkezik, amely tökéletesen semlegesíti a golyók teljes töltését. 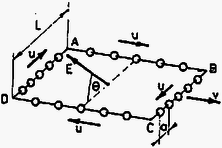    4. ábra   Tekintsük azt az esetet, amikor a hurok az $AB$ oldallal párhuzamosan $v$ sebességgel mozog egy olyan tartományban, ahol a hurok sebességére merőleges $E$ térerősségű homogén elektromos mező van. A hurkot mindvégig egy olyan síkban mozgatjuk, amely $\Theta$ szöget zár be az $E$ térerősség irányával. A relativisztikus effektusokat figyelembe véve, számítsd ki a következő mennyiségeket egy olyan megfigyelő vonatkoztatási rendszeréhez képest, aki a hurkot a fenti $v$ sebességgel mozgónak látja: a) A golyók közti távolságokat a hurok minden egyes oldalára: $\begin{array}{c}{\displaystyle a_{AB}\mathrm{,}{a}_{BC}\mathrm{,}{a}_{CD}\mathrm{,}\text{és}{a}_{DA}\mathrm{.}}\end{array}$ b) Az eredő töltés értékét (hurok és golyók) a hurok minden egyes oldalára: $\begin{array}{c}{\displaystyle Q_{AB}\mathrm{,}{Q}_{BC}\mathrm{,}{Q}_{CD}\text{és}{Q}_{DA}\mathrm{.}}\end{array}$ c) Az elektromos hatásokból létrejövő $M$ forgatónyomatékot, amely a hurkot a golyókkal együtt forgatni igyekszik. d) A $W$ energiát, amely a huroknak, illetve a golyóknak az elektromos mezővel való elektrosztatikus kölcsönhatásából származik. Minden egyes választ a feladat adataival (jelölésével) kell megadni!   Útmutatás: Egy test elektromos töltése független attól a vonatkoztatási rendszertől, amelyben megmérjük értékét. A feladatban a sugárzási hatásokat elhanyagolhatjuk.   A speciális relativitáselmélet néhány formulája:   1. Tekintsük az $S\text{'}$ vonatkoztatási rendszert, amely $v$ sebességgel mozog egy másik $S$ vonatkoztatási rendszerhez képest. A rendszerek tengelyei párhuzamosak. $v$ iránya az $x$ tengely pozitív irányával egyezik meg. Ha egy részecske az $S\text{'}$-ben mérve $u\text{'}$ sebességgel mozog az $x\text{'}$ irányban, akkor a részecske $S$-ben mért sebessége: $\begin{array}{c}{\displaystyle u=\frac{u\text{'}+v}{1+u\text{'}v/c^2}\mathrm{,}}\end{array}$ továbbá mozgásának iránya $x$-tengely menti (ez a relativisztikus sebességösszeadás). 2. Ha egy test hossza nyugalomban $L_0$, akkor amint egy megfigyelőhöz képest $v$ sebességgel mozog $L_o$ irányában, ez a megfigyelő a következő $L$ hosszat méri: $\begin{array}{c}{\displaystyle L=L_0\sqrt[]{1-v^2/c^2}\mathrm{.}}\end{array}$   Megoldás. a) Két relativisztikus hatást kell figyelembe venni: a Lorentz-kontrakciót és a relativisztikus sebességösszeadást. Abban a koordináta-rendszerben, melyben a golyók nyugalomban vannak, $a_{ny}$ távolságuk egymástól így adható meg: $\begin{array}{c}{\displaystyle a_{ny}=\frac{a}{\sqrt[]{1-u^2/c^2}}\mathrm{,}}\end{array}$ ami a hurok mindegyik oldalára érvényes. A nyugvó megfigyelő az $AB$ oldalon mozgó golyók sebességét $u_{AB}$-nek látja: $\begin{array}{c}{\displaystyle u_{AB}=\frac{v+u}{1+uv/c^2}\mathrm{,}}\end{array}$ így a golyók közti távolság a megfigyelő rendszerében: $\begin{array}{c}{\displaystyle a_{AB}=\sqrt[]{1-\frac{u_{AB}^2}{c^2}}\cdot a_{ny}=\frac{\sqrt[]{1-v^2/c^2}}{1+uv/c^2}\cdot a\mathrm{.}}\end{array}$ A $CD$ oldal esetén a számítás a fentiekkel azonos módon történik, azzal a különbséggel, hogy ekkor $u$ előjelet vált $v$-hez képest. A megfigyelő a $CD$ oldalon a golyók távolságát $\begin{array}{c}{\displaystyle a_{CD}=\frac{\sqrt[]{1-v^2/c^2}}{1-uv/c^2}a}\end{array}$ értékűnek látja. Mivel a keret a megfigyelőhöz képest $AD$, illetve $BC$ irányban nem mozdul el, így: $\begin{array}{c}{\displaystyle a_{BC}=a_{DA}=a\mathrm{.}}\end{array}$ b) A hurokhoz rendelt vonatkoztatási rendszerben bármely oldalra, az oldalt alkotó huzal töltése: $\begin{array}{c}{\displaystyle Q_{\text{huzal}}=-\frac{L}{a}q\mathrm{,}}\end{array}$ hiszen az egyes oldalakon lévő golyók száma $L/a$. Mivel a töltés relativisztikus invariáns, ez az érték bármely oldalra ugyanekkora a megfigyelő rendszerében is. A megfigyelő az $AB$ oldalt $\sqrt[]{1-v^2/c^2}\cdot L$ hosszúságúnak látja, ahol a golyók távolsága $a_{AB}$, így az $AB$ oldalon lévő golyók töltése a nyugvó vonatkoztatási rendszerben: $\begin{array}{c}{\displaystyle Q_{AB\mathrm{,}\text{golyók}}=\frac{\sqrt[]{1-v^2/c^2}\cdot L}{a_{AB}}\cdot q=\left(1+\frac{uv}{c^2}\right)\frac{L}{a}q\mathrm{,}}\end{array}$ illetve az $AB$ oldalon lévő eredő töltés: $\begin{array}{c}{\displaystyle Q_{AB}=\frac{uv}{c^2}\frac{L}{a}q\mathrm{.}}\end{array}$ Ugyanezt az eljárást követve, a $CD$ oldal eredő töltése $\begin{array}{c}{\displaystyle Q_{CD}=-\frac{uv}{c^2}\frac{L}{a}q\mathrm{.}}\end{array}$ A $BC$ és $DA$ oldalakon lévő golyók töltése: $\begin{array}{c}{\displaystyle Q_{BC\mathrm{,}\text{golyók}}=Q_{DA\mathrm{,}\text{golyók}}=Lq/a\mathrm{,}}\end{array}$ így ezeken az oldalakon az eredő töltés: $\begin{array}{c}{\displaystyle Q_{BC}=0\text{és}{Q}_{DA}=0.}\end{array}$ c) Az $AB$ oldalra ható elektrosztatikus erő $\begin{array}{c}{\displaystyle {\overrightarrow{F}}_{AB}=Q_{AB}\overrightarrow{E}=\left(uv/c^2\right)\frac{L}{a}q\overrightarrow{E}\mathrm{,}}\end{array}$ míg a $CD$ oldalra ható elektromos erő 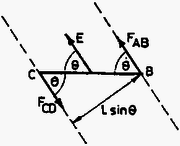$\begin{array}{c}{\displaystyle {\overrightarrow{F}}_{CD}=Q_{CD}\overrightarrow{E}=\left(uv/c^2\right)\frac{L}{a}q\overrightarrow{E}\mathrm{.}}\end{array}$     5. ábra   A fenti két erő erőpárt alkot, melynek forgatónyomatéka az 5. ábrának megfelelően $\begin{array}{c}{\displaystyle M=|{\overrightarrow{F}}_{AB}|L\cdot \text{sin}\Theta =\frac{uv}{c^2}\frac{L^2}{a}|q||\overrightarrow{E}|\cdot \text{sin}\Theta \mathrm{.}}\end{array}$ d) Ha az $AB$ és $CD$ oldalak elektrosztatikus potenciáljai rendre $U_{AB}$ és $U_{CD}$, akkor a $W$ kölcsönhatási energia $\begin{array}{c}{\displaystyle W=U_{AB}{Q}_{AB}+U_{CD}{Q}_{CD}\mathrm{.}}\end{array}$ Rögzítsük a potenciál null-értékét ($U=0$) $\overrightarrow{E}$-re merőlegesen az $AB$ oldaltól tetszőleges $R$ távolságban (lásd a 6. ábrát). 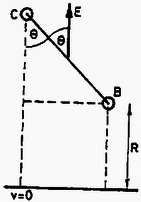    6. ábra   Ekkor $\begin{array}{c}{\displaystyle W=-ER{Q}_{AB}-E\left(R+L\cdot \text{cos}\Theta \right)q_{CD}\mathrm{.}}\end{array}$ Mivel $\begin{array}{c}{\displaystyle Q_{CD}=-Q_{AB}\mathrm{,}}\end{array}$ így $\begin{array}{c}{\displaystyle W=EL{Q}_{AB}\cdot \text{cos}\Theta =\frac{uv{L}^{2}qE}{c^{2}a}\cdot \text{cos}\Theta \mathrm{.}}\end{array}$   3. feladat. Atomok hűtése lézerrel   Különálló atomok tulajdonságainak nagy pontosságú vizsgálatához az atomokat csaknem nyugalomban kell tartani bizonyos ideig a tér egy kis tartományában. Ennek elérésére a közelmúltban új módszert dolgoztak ki, amit ,,lézerhűtés''-nek hívnak. A feladat ezzel kapcsolatos. Egy vákuumkamrában egy erősen kollimált (párhuzamosított) ${\text{Na}}^{23}$ atomokból álló sugarat (melyet egy ${10}^3\text{ K}$ hőmérsékletű térben párologtatással kapunk) szemből megvilágítunk egy nagy intenzitású lézersugárral (7. ábra). 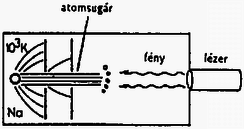    7. ábra   A lézer frekvenciáját úgy választjuk meg, hogy fotonjai rezonancia-abszorpcióba kerüljenek azokkal az atomokkal, amelyeknek sebessége $v_0$. A fény abszorpciójakor (elnyelésekor) az atom az első gerjesztett energiaszintre kerül, amelynek energiája $E$ és szélessége $\Gamma$ (8. ábra). Az atom sebessége a következőképpen változik meg: 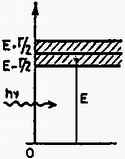$\Delta v_1=v_1-v_0\mathrm{.}$     8. ábra   Ezután az atom újra fényt sugároz ki, így alapállapotba tér vissza, sebessége $\Delta v\text{'}=v{\text{'}}_1-v_1$ értékkel, míg mozgásának iránya $\phi$ szöggel változik (9. ábra). 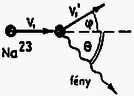    9. ábra   Az elnyelődések és kisugárzások egymást követő fenti eseményei nagyon sokszor megismétlődnek, egészen addig, amíg az atomok sebessége egy adott $\Delta v$ értékkel meg nem változik úgy, hogy a rezonancia-abszorpció $\nu$ frekvenciájú fénnyel tovább már nem mehet végbe. Ekkor szükségessé válik a lézer frekvenciájának olyan megváltoztatása, hogy a rezonancia-abszorpció az új sebesség mellett is lejátszódjon, és ezt egészen addig kell folytatni, amíg az atomok közül néhánynak a sebessége csaknem zérussá válik. A folyamat első közelítésében elhanyagolhatunk minden más atomi kölcsönhatási folyamatot a spontán abszorpción (elnyelődésen), illetve kisugárzáson kívül. Továbbá feltehetjük, hogy a lézer intenzitása olyan nagy, hogy az atomok gyakorlatilag nem töltenek időt alapállapotban. Adatok: ${\displaystyle \begin{array}{c}\hfill {\displaystyle E=\mathrm{3,36}\cdot {10}^{-19}\text{ J}\mathrm{,}\Gamma =\mathrm{7,0}\cdot {10}^{-27}\text{ J}\mathrm{,}c=\mathrm{3,0}\cdot {10}^8\text{ m/s}\mathrm{,}}\hfill \\ \hfill {\displaystyle m_p=\mathrm{1,67}\cdot {10}^{-27}\text{ kg}\mathrm{,}h=\mathrm{6,62}\cdot {10}^{-34}\text{ Js}\mathrm{,}k=\mathrm{1,38}\cdot {10}^{-23}\text{ J/K}\mathrm{,}}\hfill \end{array}}$ ahol $c$ a fény sebessége; $h$ a Planck-állandó, $k$ a Boltzmann-állandó és $m_p$ a proton tömege.   Kérdések: a) Mekkora legyen a lézer $\nu$ frekvenciája, hogy biztosítsuk a fény rezonancia-abszorpcióját azoknak az atomoknak az esetében, amelyek mozgási energiája a kollimátor mögötti térben párolgó atomok átlagos mozgási energiájával egyezik meg? Mekkora ezeknek az atomoknak a $\Delta v_1$ sebességváltozása az első elnyelődési folyamat után? b) Mekkora $\Delta v_0$ sebességintervallumban vannak azok az atomok, amelyek fényt abszorbeálnak az a) kérdésben kiszámított frekvencia esetén? c) Egyetlen kisugárzási esemény esetén mekkora az eredeti irányhoz képesti ${\phi }_m$ maximális szögeltérés? d) Mekkora a sebességcsökkenés $\Delta v$ határértéke a $\nu$ frekvencia megváltozása nélkül? e) Hozzávetőlegesen add meg az elnyelődési-kisugárzási eseményeknek az $N$ számát, amely szükséges ahhoz, hogy egy egyenes mentén haladó, és (az a) kérdésben említett) $v_0$ sebességű atom sebessége csaknem zérusra csökkenjen! f) Mekkora $\Delta t$ idő alatt játszódik le az utóbbi folyamat? Mekkora $\Delta s$ távolságot tesz meg ennyi idő alatt az atom?   Megoldás a) A kollimátort elhagyó atomok átlagos mozgási energiájából a következő $v_0$ sebességet határozhatjuk meg: $\frac{1}{2}m{v}_0^2=\frac{3}{2}kT$, amiből $\begin{array}{c}{\displaystyle v_0=\sqrt[]{\frac{3kT}{m}}\approx \mathrm{1,04}\cdot {10}^3\frac{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}\mathrm{.}}\end{array}$ Mivel $v_0\ll c$, így elhanyagolhatjuk a relativisztikus effektusokat.  A fénysugarat alkotó fotonok energiája $h\nu$, impulzusuk $h\nu /c$. Alkalmazzuk az energia- és az impulzusmegmaradás törvényét a laboratóriumi vonatkoztatási rendszerben az elnyelődési folyamatra: $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}_0^2+h\nu =\frac{1}{2}m{v}_1^2+E;m{v}_0-\frac{h\nu }{c}=m{v}_1\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle \Delta v_1=v_1-v_0=-\frac{h\nu }{mc}\mathrm{,}}\end{array}$ továbbá $\begin{array}{c}{\displaystyle \frac{1}{2}m\left(v_1^2-v_0^2\right)=h\nu -E\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle \frac{1}{2}m\left(v_1+v_0\right)\left(v_1-v_0\right)=h\nu -E\mathrm{.}}\end{array}$ Felhasználva, hogy $h\nu \ll m{v}_0$, így $v_1\approx v_0$, a fenti egyenlet így egyszerűsíthető: $\begin{array}{c}{\displaystyle m{v}_0\Delta v_1=h\nu -E\mathrm{,}}\end{array}$ ahol feltettük, hogy $v_1+v_0\approx 2v_0$. Ezeknek az egyenleteknek a felhasználásával $\begin{array}{c}{\displaystyle \nu =\frac{E/h}{1+v_0/c}\approx \mathrm{5,0}\cdot {10}^{14}\text{Hz}\mathrm{.}}\end{array}$ illetve $\begin{array}{c}{\displaystyle \Delta v_1=-\frac{E}{mc}\frac{1}{1+v_0/c}\approx -\mathrm{3,0}\cdot {10}^{-2}\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$ b) Rögzített $\nu$ frekvencia esetén: $\begin{array}{c}{\displaystyle v_0=c\left(\frac{E}{h\nu }-1\right)\mathrm{.}}\end{array}$ Ha $E$ bizonytalansága $\Gamma$, $v_0$ bizonytalansága $\Delta v_0$ lesz: $\begin{array}{c}{\displaystyle \Delta v_0=\frac{c\Gamma }{h\nu }=\frac{c\Gamma \left(1+v_0/c\right)}{E}\approx \frac{c\Gamma }{E}=\mathrm{6,25}\frac{\text{m}}{\text{s}}\mathrm{,}}\end{array}$ így azok az atomok nyelnek el fotonokat, melyek sebessége a következő intervallumba esik: $\begin{array}{c}{\displaystyle \left(v_0-\Delta v_0/\mathrm{2,}{v}_0+\Delta v_0/2\right)\mathrm{.}}\end{array}$ c) Írjuk fel kisugárzás esetén is az energia- és az impulzusmegmaradás törvényét: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{1}{2}m{v}_1^2+E=\frac{1}{2}mv\text{'}{}_1^2+h\nu \text{'}\mathrm{,}}\hfill \\ \hfill {\displaystyle m{v}_1=mv{\text{'}}_1\text{cos}\phi +\frac{h\nu \text{'}}{c}\text{cos}\Theta \mathrm{,}}\hfill \\ \hfill {\displaystyle 0=mv{\text{'}}_1\text{sin}\phi -\frac{h\nu \text{'}}{c}\text{sin}\Theta \mathrm{,}}\hfill \end{array}}$ ahol $\nu \text{'}$ a kisugárzott foton frekvenciája. Az atom $\phi$ szögeltérése akkor maximális, ha $\Theta =\frac{\pi }{2}$, vagyis $\begin{array}{c}{\displaystyle m{v}_1=mv{\text{'}}_1\cdot \text{cos}{\phi }_m\text{és}\frac{h\nu \text{'}}{c}=mv{\text{'}}_1\cdot \text{sin <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>φ</mi></mrow><mrow><mi>m</mi></mrow></msub></mrow></math>,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle \text{tg}{\phi }_m=\frac{h\nu \text{'}}{m{v}_{1}c}\mathrm{.}}\end{array}$ Mivel $\begin{array}{c}{\displaystyle \nu \text{'}\approx \nu \mathrm{,}\text{így}\text{tg}{\phi }_m\approx \frac{E}{m{v}_{1}c}\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle {\phi }_m\approx 5\cdot {10}^{-5}\text{rad}\mathrm{.}}\end{array}$ d) Az atomok sebességének csökkenésekor a rezonancia-elnyelődéshez szükséges frekvenciának növekednie kell a már megismert $\nu =\frac{E/h}{1+v_0/c}$ összefüggésnek megfelelően. Ha a sebesség $v_0-\Delta v$, az elnyelődés az energiaszint alsó részén akkor marad csak lehetséges, ha: $\begin{array}{c}{\displaystyle h\nu =\frac{E-\Gamma /2}{1+\left(v_0-\Delta v\right)/c}=\frac{E}{1+v_0/c}\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle \Delta v=\frac{c\Gamma }{2E}\left(1+v_0/c\right)=\mathrm{3,12}\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$ e) Ha minden elnyelődési‐kisugárzási esemény $\Delta v_1\approx -\frac{E}{mc}$ értékkel változtatja meg a sebességet, akkor ahhoz, hogy a $v_0$ sebesség csaknem nullára csökkenjen $\begin{array}{c}{\displaystyle N=|\frac{v_0}{\Delta v_1}|\approx \frac{mc{v}_0}{E}\approx \mathrm{3,56}\cdot {10}^4}\end{array}$ esemény szükséges. f) Ha az elnyelődés pillanatszerű, akkor a folyamathoz szükséges időt a spontán kisugárzás határozza meg. Az atom a Heisenberg-féle határozatlansági reláció idő‐energia összefüggésének megfelelően bizonyos ideig gerjesztett marad: $\tau =h/\Gamma$. Így a kívánt idő: $\begin{array}{c}{\displaystyle \Delta t=N\tau =\frac{Nh}{\Gamma }=\frac{mch{v}_0}{\Gamma E}\approx \mathrm{3,37}\cdot {10}^{-3}\text{s}\mathrm{.}}\end{array}$ Az ezalatt megtett távolság $\Delta s=v_0\Delta t/2$, feltéve, hogy a mozgás egyenletesen lassuló. Így: $\begin{array}{c}{\displaystyle \Delta s=\frac{1}{2}\frac{mch{v}_0^2}{\Gamma E}\approx \mathrm{1,75}\text{m}\mathrm{.}}\end{array}$   Kísérleti feladat. A versenyzőknek egy három kivezetésű fekete dobozt kellett vizsgálniuk, meg kellett állapítaniuk, mi van benne, milyen a kapcsolási rajz, melyek az egyes áramköri elemek jellemző értékei és milyen mérési pontossággal tudják ezt meghatározni. A méréshez változtatható egyenfeszültségű tápegység, két mérőműszer, adott ellenállások, adott értékű kondenzátor, stopperóra stb. álltak rendelkezésre. A feladat szövege tartalmazta azt a segítséget, hogy három különböző áramköri elem van a dobozban, melyek a következő négy típusból kerülhetnek ki: telep, ellenállás, kondenzátor, félvezető dióda. A helyes kapcsolási rajzot a 10. ábra mutatja. 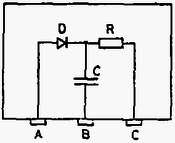    10. ábra