Kezdőlap


Cím:	1990. Beszámoló az Eötvös-versenyről
Szerző(k):	Radnai Gyula
Füzet:	1991/február, 81 - 86. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Lemezjátszó korongjának közepére helyezett tálban víz van. A vízen egy pingponglabda úszik. Mi történik a pingponglabdával, miután megindítottuk a lemezjátszót?

Megoldás. Miután megindítottuk a lemezjátszót, a tálban a víz a koronggal együtt forog. A közel azonos szögsebességet a víz belső súrlódása biztosítja. A viszonylag alacsony fordulatszám miatt turbulencia nem lép fel.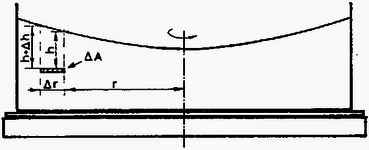

1. ábra

A felület közelítőleg forgásparaboloid alakú, amint az ‐ inerciarendszerből ‐nézve az alábbi módon látható:

\begin{matrix} F = m \cdot a, \end{matrix}

s ezt az összefüggést egy kicsiny

Δ A

alapterületű,

Δ r

,,magasságú'' folyadékdarabkára alkalmazva

\begin{matrix} [ϱ g (h + Δ h) - ϱ g h] Δ A = Δ A \cdot Δ r \cdot ϱ \cdot ω^{2} r . \end{matrix}

Egyszerűsítések után:

\begin{matrix} g \cdot Δ h = ω^{2} r \cdot Δ r, \\ \frac{Δ h}{Δ r} = \frac{ω^{2} r}{g} . \end{matrix}

A bal oldalon ‐ határátmenetben ‐ az érintő meredeksége áll; a vízszintessel bezárt hajlásszöggel kifejezve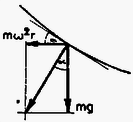

\begin{matrix} tg α = \frac{ω^{2} r}{g} . \end{matrix}

2. ábra

Ezt az összefüggést közvetlenül is megkaphatjuk, ha gyorsuló (

ω

szögsebességgel forgó) koordinátarendszerből írjuk le a jelenséget. Felhasználva, hogy a folyadék szabad felülete minden pontjában merőleges az ott ható külső erők eredőjére:

\begin{matrix} tg α = \frac{ω^{2} r}{g} . \end{matrix}

A görbe meredekségét ismerve integrálással kaphatjuk meg a görbe egyenletét:
Ha

y' = \frac{ω^{2}}{g} x, akkor y = \frac{ω^{2}}{2 g} x^{2},

amennyiben az origó a görbe legalsó pontja. A parabola

y = c \cdot x^{2}

egyenletét kaptuk, tehát a felület valóban forgásparaboloid.
Vizsgáljuk meg a vízen úszó pingponglabdára ható erőket! A jelenséget a továbbiakban végig az

ω

szögsebességgel forgó koordinátarendszerben írjuk le, de megkülönböztetünk egymástól két esetet aszerint, hogy figyelembe vesszük-e a levegő közegellenállását, vagy sem.
Először tekintsünk el a levegő közegellenállásától. Ekkor a pingponglabdára háromféle erő hat: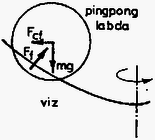

3. ábra

1. A nehézségi erő

(m g)

; koncentrálható a pingponglabda tömegközéppontjába.
2. A centrifugális erő

(F_{c f})

ugyancsak a pingponglabda középpontjába koncentrálható (ezt az állítást azonban még be kell bizonyítanunk).
3. A felhajtóerő

(F_{f})

a kiszorított víz volt tömegközéppontjába koncentrálható.
A pingponglabdára ható erők eredőjének meghatározásához bontsuk fel a felhajtóerőt is függőleges és vízszintes összetevőkre. Mekkora a vízszintes összetevő? Amekkora a kiszorított vízre ható centrifugális erő volt. A kiszorított víz tömege jó közelítéssel megegyezik a pingponglabda tömegével. (Egyensúly esetén egyezne meg vele pontosan.) Írhatjuk tehát:

\begin{matrix} F_{f vízsz.} = m ω^{2} r_{1}, \end{matrix}

ahol

r_{1}

jelenti a kiszorított víz volt tömegközéppontjának távolságát a forgástengelytől.
A pingponglabdára ható centrifugális erő nagysága: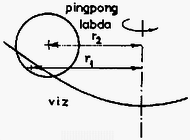

\begin{matrix} F_{c f} = m ω^{2} r_{2}, \end{matrix}

ahol

r_{2}

a labda középpontjának távolsága a forgástengelytől (4. ábra).

4. ábra

Igen ám, de

\begin{matrix} r_{2} < r_{1}, \end{matrix}

hiszen a labda kiemelkedik a ferde vízfelületből, s ezért középpontja közelebb van a forgástengelyhez, mint a vízbe merülő részé!
A pingponglabdára tehát egy ,,befelé'' mutató eredő erő hat mindaddig, amíg csak a labda be nem úszik középre. Ezután ott marad, egyensúlyi helyzete stabilis lesz.
Hátra van még annak bizonyítása, hogy a labdára ható centrifugális erő a labda középpontjába koncentrálható, pontosabban a centrifugális erő nagysága és iránya ugyanakkora, mintha a labda teljes tömege a tömegközéppontban volna.
A bizonyítást Bodor András versenynyertes dolgozatából idézzük, aki egy szellemes ötlettel egyszerűsítette le ezt az első pillanatra bonyolultnak látszó problémát.
,,Vágjuk fel a labdát a forgástengelyre merőleges síkokkal vékony körgyűrűkre. Elég belátnunk, hogy akármelyik gyűrűre ható centrifugális erő nagysága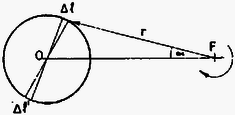

\begin{matrix} R ω^{2} m_{gyűrű}, \end{matrix}

ahol

R

a gyűrű középpontjának és a forgástengelynek a távolsága

5. ábra

Osszuk fel a gyűrűt

n

darab kis

Δ l

hosszú részre; legyen az egységnyi hosszú kerületdarab tömege

p

. Ekkor a gyűrűre ható centrifugális erő:

\begin{matrix} F_{c f} = \sum Δ l ϱ r ω^{2} . \end{matrix}

Az nyilvánvaló, hogy ez az összeg a középpontot a forgástengellyel összekötő egyenessel (

O F

) párhuzamos lesz, ezért elég az összegzéskor csak az

O F

egyenessel párhuzamos komponensek összegét venni:

\begin{matrix} F_{c f} = \sum Δ l ϱ r cos α \cdot ω^{2} . \end{matrix}

Vegyünk most egy kis

Δ l

szakaszt és ennek a gyűrű középpontjára vett tükörképét,

Δ l'

-t. Ezek hossza egyenlő. A kettejükre ható centrifugális erők összege

\begin{matrix} F_{c f 1,2} = Δ l ϱ ω^{2} (r_{1} cos α_{1} + r_{2} cos α_{2}) . \end{matrix}

Mivel

r_{1} cos α_{1} + r_{2} cos α_{2} = 2 \bar{O F} = 2 R

, így párosával véve a kis

Δ l

szakaszokat

\begin{matrix} F_{c f} = \sum_{}^{n} Δ {l ϱ ω}^{2} r cos α = \sum_{}^{n / 2} Δ l ϱ ω^{2} \cdot 2 R = R ω^{2} ϱ \sum_{}^{n / 2} 2 Δ l = R ω^{2} \cdot m . \end{matrix}

Tehát a pingponglabdára ható centrifugális erő valóban

R ω^{2} m

.''

Megjegyezzük, hogy a centrifugális erő nagysága akármilyen alakú test esetében az össztömeg és a tömegközéppont helyzetének megfelelő

R ω^{2}

gyorsulás szorzata; ez következik az inerciarendszerben megfigyelhető mozgásra felírható tömegközépponttételből. A centrifugális erő hatásvonala azonban általában nem megy át a tömegközépponton.
Végül vizsgáljuk meg azt az esetet, amikor nem tekinthetünk el a levegő közegellenállásától. A levegő nem forog együtt a rendszerrel, ezért fékezi a labdát. A labda szögsebessége kisebb, mint a kiszorított víz szögsebessége volt. Ezáltal a centrifugális erő még kisebb, mint a közegellenállás nélküli esetben, s a labdára ható Coriolis erő (mivel a labda most mozog a forgó vízhez képest) ugyancsak befelé mutat. Még hamarabb, még gyorsabban úszik be középre a pingponglabda.

2. Vízszintes helyzetű körlemezekből álló síkkonderzátort feltöltünk. A kondenzátor közelében a lemezek közti távolságot felező vízszintes síkban kis iránytűt helyezünk el. Ezután a kondenzátort a függőleges szimmetriatengely körül forgásba hozzuk. Megmozdul-e az iránytű, s ha igen, merre?

Megoldás. A kondenzátoron lévő töltéseket körmozgásra kényszerítjük azáltal, hogy a kondenzátort megforgatjuk. Lehet, hogy a töltéssűrűség kifelé haladva kissé nőni fog, ez azonban semmit sem változtat azon a tényen, hogy lényegében szimmetrikus köráramok (6.ábra) mágneses terének eredőjét kell meghatároznunk.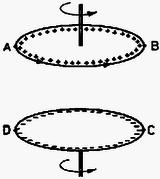

6. ábra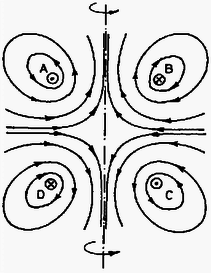

7. ábra

A 7. ábrán két ilyen szimmetrikus köráram eredő mágneses terének

B

-vonalait ábrázoltuk egy, a forgástengelyen átmenő, függőleges síkban. Minden

B

-vonal benne van egy-egy, a forgástengelyen is átmenő függőleges síkban. Ezen síkok közül választottunk ki egyet az ábrán.
A lemezek közötti távolságot felező vízszintes síkban, a kondenzátor közelében helyezkedik el az iránytű. Szimmetria okok miatt az áramokból származó

B

vektor ezen a helyen pontosan a forgástengely felé mutat (ez látható az ábrán megrajzolt esetben), vagy ezzel az iránnyal éppen ellentétes, ha akár a töltések előjele, akár a forgásirány az ábrán felrajzolthoz képest ellentétes.
A kondenzátor mozgó töltéseinek fenti mágneses tere a földi mágneses térre szuperponálódik, azt elvileg módosítja. (Gyakorlatilag csak kevéssé, ezért a jelenséget iskolai körülmények között nem lehet megfigyelhetővé tenni.)
Az iránytű, amely a földi mágneses térnek megfelelően állt be, biztosan nem mozdul meg a kondenzátor megforgatásakor, ha a mozgó töltésektől származó

B

az iránytű helyén a földi

B

-vel pontosan megegyező vagy ellentétes irányú. Minden más esetben az eredő

B

a földi

B

-től némileg eltérő irányú, ezért az iránytűnek elvileg el kell fordulnia, hogy beállhasson az eredő

B

irányába.

3. Vízben szuszpendált,

d = 0,5 μ m

átmérőjű gömb alakú részecskék termikus egyensúlyi eloszlását vizsgáljuk mikroszkópon keresztül. A mikroszkóp tubusa függőleges. A részecskék anyagának sűrűsége

1040 {k g / m}^{3}

, a hőmérséklet

23^{\circ} C

. A mikroszkóp mélységélessége kicsi, mindig csak egy igen vékony vízrétegben lévő részecskék láthatóak élesen. Mennyivel kell lejjebb süllyeszteni a mikroszkóp tubusát, hogy kétszer annyi részecskét lássunk? A víz törésmutatója

n = 1, 33

Megoldás. Mivel a részecskék átmérője a látható fény hullámhosszával azonos nagyságrendű, ezért egy-egy részecske éles képe a mikroszkóp sötét látóterében egy-egy világító pont.
A részecskék magasság szerinti eloszlása az állandó hőmérsékletű vízben Boltzmann-eloszlás lesz. Ennek megfelelően a

h_{1}

és

h_{2}

magasságban elhelyezkedő részecskék átlagos számának aránya:

\begin{matrix} \frac{N_{2}}{N_{1}} = e^{- [E (h_{2}) - E (h_{1})] / (k T)} . \end{matrix}

Hogyan lehet meghatározni a

h

magasságban lévő részecske

E (h)

potenciális (magassági) energiáját? Vegyük figyelembe, hogy a részecskére nem csak a nehézségi erő, hanem a felhajtóerő is hat. Ekkor

\begin{matrix} E (h) = (ϱ - ϱ_{víz}) V g h, V = \frac{4}{3} r^{3} π = \frac{1}{6} d^{3} π . \end{matrix}

A fenti egyenletekből a

Δ h = h_{1} - h_{2}

magasságkülönbség:

\begin{matrix} Δ h = \frac{6 k T \cdot ln (N_{2} / N_{1})}{(ϱ - ϱ_{víz}) \cdot d^{3} π g} . \end{matrix}

A mikroszkóp tubusát azonban nem kell ennyivel lejjebb süllyeszteni, mivel vízbe kell nézni. (A vízben lévő tárgyak ,,felemelkedve'' látszanak.)
A helyes válasz:

\begin{matrix} Δ h' = \frac{Δ h}{n} . \end{matrix}

Adatok:

N_{2} / N_{1} = 2

ϱ = 1040 {kg/m}^{3}

d = 5 \cdot 10^{- 7}

g = 9, 81 {m/s}^{2}

k = 1, 38 \cdot 10^{- 23}

J/K,

T = 296

n = 1, 33

.
A víz sűrűsége

23^{\circ} C

-on a középiskolai fizikai táblázatokban lévő adatokból interpolációval kapható:

ϱ_{víz} = 997, 5 {kg/m}^{3}

, de elfogadható volt az is, ha valaki a szokásos

1000 {kg/m}^{3}

-rel számolt.
A helyes végeredmény (

5 %

pontossággal):

\begin{matrix} Δ h' = 0, 08 mm . \end{matrix}

A mikroszkóp tubusát tehát

0, 08

milliméterrel kell lejjebb süllyeszteni.

A verseny végeredménye

A Versenybizottság a beérkezett 242 dolgozat átvizsgálása után az alábbi határozatot hozta:

Első díjat és 3000 Ft jutalmat kap

BODOR ANDRÁS, az ELTE Apáczai Csere János Gyakorló Gimnáziumának IV. osztályos tanulója, Zsigri Ferenc tanítványa.

Második díjat és egyenként 2000 Ft jutalmat kap

HORVÁTH TIBOR, a kecskeméti Katona József Gimnázium IV. osztályos tanulója, Kocsisné Domján Erzsébet tanítványa, valamint ZÓKA GÁBOR, a BME I. éves villamosmérnök hallgatója, aki Nagyatádon, az Ady Endre Gimnáziumban érettségizett, mint Knapp Ottó tanítványa.

Harmadik díjat és egyenként 1500 Ft jutalmat kap

EGYEDI PÉTER, a pécsi Leőwey Klára Gimnázium IV. osztályos tanulója, Csikós Istvánné tanítványa, MARÓTI MIKLÓS, a szegedi Radnóti Miklós Gimnázium IV. osztályos tanulója, Dudás Zoltánné tanítványa, valamint TOKODI TAMÁS, a JATE I. éves fizikus hallgatója, aki Szegeden, a JATE Ságvári Endre Gyakorló Gimnáziumában érettségizett, mint Kocsis Vilmos és Győri István tanítványa.

Dicséretet és egyenként 500 FT értékű könyvutalványt kap a verseny 7-13. helyezettje:

7. HEGEDŰS PÁL, a soproni Berzsenyi Dániel Gimnázium IV. osztályos tanulója, Lang Jánosné tanítványa. 8. KISS GYULA, a zalaegerszegi Zrínyi Miklós Gimnázium IV. osztályos tanulója, Pálovics Róbert tanítványa. 9. FALUS PÉTER, az ELTE Ságvári Endre Gyakorló Gimnáziumának IV. osztályos tanulója, Honyek Gyula tanítványa. 10. GULYÁS FERENC, a pécsi Zipernovszky Károly Ipari Szakközépiskola IV. osztályos tanulója, Kiss Jenő tanítványa. 11. CSILLING ÁKOS, az ELTE I. éves fizikus hallgatója, aki Budapesten, a Fazekas Mihály Gimnáziumban érettségizett, mint Horváth Gábor tanítványa. 12. FÖLDVÁRI ZOLTÁN, a veszprémi Lovassy László Gimnázium IV. osztályos tanulója, Farkas István tanítványa. 13. BILICS PÉTER, a budapesti Fazekas Mihály Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa.

A Versenybizottság további sorrendet nem állapított meg, és ezúton is gratulál a verseny nyerteseinek.