Kezdőlap


Cím:	Az 1991. évi Arany Dániel Matematikai Tanulóverseny
Füzet:	1991/november, 354 - 363. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1991. évi
Arany Dániel Matematikai Tanulóverseny
feladatai
I. forduló
Kezdők (legfeljebb I. Osztályosok)

a

b

c

d

e

pozitív egész számokról tudjuk, hogy

a \cdot b \cdot c = 22

és

c \cdot d \cdot e = 181

. Mennyi lehet az

a \cdot b \cdot c \cdot d \cdot e

?
(6 pont)

2. Adja meg a valós

x

értékekre értelmezett

K (x)

kifejezés legkisebb értékét, ha

\begin{matrix} K (x) = | 1 - x | + | 2 - x | + | 3 - x | . \end{matrix}

(6 pont)

3. Oldja meg a valós számok halmazán a következő egyenletet:

\begin{matrix} 8 [\frac{x}{4}] = | x - 4 | . \end{matrix}

(

[z]

: a

z

szám egészrészét jelenti, azt a legnagyobb egész számot, ami nem nagyobb

z

-nél.)
(6 pont)

4. Keresse meg

1990^{1991} - 1991^{1990}

összes

10

-nél kisebb pozitív egész osztóját!
(8 pont)

5. Az

A B C D

téglalap átlóinak metszéspontja

Q

C

csúcsból kiinduló szögfelezője az

A B

oldalt

E

belső pontban, a

D B

átlót

F

pontban metszi. Tudjuk, hogy az

E Q B

és

E Q F

háromszögek egyenlő szárúak. Mekkora szöget zár be a

C

pontból kiinduló szögfelező az átlókkal?
(8 pont)

6. Hány olyan

1991

jegyű, hárommal osztható szám van, melynek mindegyik számjegye az

1

3

5

számok valamelyike?
(8 pont)

7. Igazolja, hogy bármely háromszögben található két olyan oldal, melyek hosszai különbségének abszolút értéke kisebb, mint a kerület hatodrésze.
(10 pont)

8. Egy kocka középpontja, csúcspontjai, éleinek felezőpontjai és lapjainak középpontjai egy huszonhét pontból álló kockarácsot alkotnak. "Triónak'' nevezünk három pontot, ha valamelyik lapra való merőleges vetületük egyetlen pont. Határozza meg azt a legnagyobb

k

számot, melyre teljesül a következő: bárhogy véve

k

triót, van olyan trió, amelynek nincs közös pontja ezek egyikével sem.
(10 pont)

Haladók (II. osztályosok)

1. Határozzuk meg, hogy mely valós

x

értékekre értelmezhető a

\begin{matrix} \sqrt[]{\frac{x - 8 \sqrt[]{x} + 12}{5 \sqrt[]{x} - x}} kifejezés . \end{matrix}

(6 pont)

2. Az

A B

alapú

A B C

és

A B D

egyenlő szárú háromszögek közül az

A B D

háromszög tartalmazza az

A B C

háromszöget. A

C A D

szög és a

C B D

szög szögfelezői merőlegesek egymásra. Bizonyítsuk be, hogy a

C

pontnak az

A B D

háromszög száraira vonatkozó tükörképei az

A B D

háromszög köré írt körön vannak.
(6 pont)

3. Mely

k

egész számokra igaz az alábbi egyenlőség?

\begin{matrix} {(k^{2} + 1)}^{2} + 4 (k + 1) (k^{2} + 1) - 4 = 0. \end{matrix}

(6 pont)

4. Előállítható-e 1990 két négyzetszám összegeként, illetve különbségeként? És 1991?
(8 pont)

5. Egy

2 n \times 2 n

méretű sakktáblán

2 n

bástyát helyeztünk el úgy, hogy minden sorban és minden oszlopban pontosan egy áll. Bizonyítsuk be, hogy valamely két szomszédos oszlopban a bástyák azonos színű mezőn állnak.
(8 pont)

6. Egy kerek asztal körül

15

ember foglal helyet adott körüljárás szerint

1

-től

15

-ig számozott székeken. Mindegyikük gondolt egy valós számot. Ezután mindenki kiszámolta a két szomszédja által gondolt szám számtani közepét. Kiderült, hogy mindenki a saját székének sorszámát kapta. Melyik számra gondolt eredetileg a

15.

széken ülő ember?
(8 pont)

7. Egy síkbeli alakzat olyan, hogy egy

O

pont körüli

19^{\circ}

-os elforgatottja önmaga. Bizonyítsuk be, hogy az alakzatot

O

körül

86^{\circ}

-kal elforgatva szintén önmagát kapjuk. Igaz-e, hogy az

O

pont körüli tetszőleges szögű forgatás az alakzatot önmagába viszi?
(10 pont)

8. Egy háromszög oldalai

a

b

c

hosszúságúak. Bizonyítsuk be, hogy:

\begin{matrix} | (a - b) (b - c) | + | (b - c) (c - a) | + | (c - a) (a - b) | < s^{2}, \end{matrix}

ahol

s

a háromszög kerületének fele.
( 10 pont)

II.forduló
Kezdők (legfeljebb I. osztályosok)

Szakközépiskolások feladatai

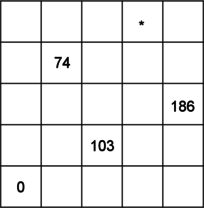
1. Az alábbi

5 \times 5

-ös négyzetrácsot ki lehet tölteni olyan pozitív egész számokkal, hogy minden sorban és minden oszlopban egy-egy számtani sorozat egymás utáni elemei helyezkedjenek el. Határozza meg a *-gal jelölt mezőbe kerülő számot.

2. Határozza meg az

a^{2} + b^{2} - a b

kifejezés legnagyobb és legkisebb értékét, ha az

a

és

b

valós számokra teljesül, hogy

| a | + | b | ≦ 1

3. Legyen a síkon

A

és

B

két különböző pont. Határozza meg ebben a síkban azoknak a

C

pontoknak a halmazát, melyeknél a sík bármely

P

pontja esetén a

P A

és

P B

távolságok közül legalább az egyik

P C

-nél nagyobb.

Az általános tantervű osztályok feladatai

1. Legyen a síkon

A

és

B

két különböző pont. Határozza meg ebben a síkban azoknak a

C

pontoknak a halmazát, melyeknél a sík bármely

P

pontja esetén a

P A

és

P B

távolságok közül legalább az egyik

P C

-nél nagyobb.

2. Az

a

b

c

d

pozitív számok szorzata egy. Legyen

\begin{matrix} A = a^{2} + b^{2} + c^{2} + d^{2} + a b + a c + a d + b c + b d + c d . \end{matrix}

Határozza meg

A

legkisebb értékét.

3. Határozza meg az összes olyan pozitív egész számot, amely valamelyik prímszám hatványa és a tízes számrendszerben

\begin{matrix} \bar{A B B A A B B A ... A B B A} \end{matrix}

alakú ("

A B B A

n

-szer egymás után,

n \geq 1

1 \leq A \leq 9

0 \leq B \leq 9

A speciális matematika tantervű osztályok feladatai

1. Bizonyítsa be, hogy tetszőleges

a

b

c

valós számok esetén

\begin{matrix} a^{2} + b^{2} + c^{2} \geq a b + b c + c a + \frac{| a - b | \cdot | b - c | + | b - c | \cdot | c - a | + | c - a | \cdot | a - b |}{2} . \end{matrix}

2. Határozza meg az összes olyan pozitív egész számot, amely valamelyik prímszám hatványa és a tízes számrendszerben

\begin{matrix} \bar{A B B A A B B A ... A B B A} \end{matrix}

alakú ("

A B B A

n

-szer egymás után,

n \geq 1

1 \leq A \leq 9

0 \leq B \leq 9

3. Tekintsük a síkon azon

(x; y)

pontokat, melyekre

x

és

y

pozitív egészek, legnagyobb közös osztójuk egy, továbbá

x \leq 1991

y \leq 1991

és

x + y > 1991

. Legyen egy ilyen pont "súlya''

\frac{1}{x y}

. Számítsa ki az említett tulajdonságú pontok súlyainak összegét.

Haladók (II. osztályosok)

Szakközépiskolások feladatai

1. Három pozitív egész szám összege

27

, reciprokaik összege

\frac{97}{204}

. Melyek ezek a számok?

2. Hányféleképpen helyezkedhetnek el öten egy ötüléses páholyban úgy, hogy legalább egy ember oda ül, ahová a jegye szól?

3. Egy egyenlő szárú háromszög súlypontja a háromszögbe írt kör kerületén van. Határozzuk meg a háromszög köré és a háromszögbe írt kör sugarának arányát!

Az általános tantervű osztályok feladatai

1. Határozzuk meg az

\begin{matrix} x \mapsto \sqrt[]{x^{2} + 16} + \sqrt[]{x^{2} - 12 x + 52}, x \in R \end{matrix}

függvény minimumát!

2. Egy egyenlő szárú háromszög súlypontja a háromszögbe írt kör kerületén van. Határozzuk meg a háromszög köré és a háromszögbe írt kör sugarának arányát!

3. Egy kerek asztal körül húsz szék áll, amelyek meg vannak számozva

1

2

3

...

19

20

számokkal, ebben a sorrendben. Megengedett művelet négy egymás után álló szék sorrendjének megfordítása (pl.

19

20

1

2

-ből

2

1

20

19

lesz). Mutassuk meg, hogy megengedett műveletek sorozatával felcserélhető az

1

-es és

2

-es szék úgy, hogy a többi sorrendje változatlan marad. (Azaz elérhető a

2

1

3

4

5

6

...

19

20

sorrend).

A speciális matematika tantervű osztályok feladatai

1. Határozzuk meg az

\begin{matrix} x \mapsto \sqrt[]{x^{2} + 16} + \sqrt[]{x^{2} - 12 x + 52}, x \in R \end{matrix}

függvény minimumát!

2. Bizonyítsuk be, hogy az

x^{2} + y^{2} + z^{2} = 3 x y z

egyenletnek végtelen sok egész megoldása van!

3. Egy kockát lapjaival párhuzamos síkokkal egybevágó kockákra vágtunk szét, majd mindegyik kisebb kockát kifestettük hat adott szín valamelyikére. A kifestésre teljesül, hogy
(a) az azonos színű kockák száma minden színre más,
(b) bárhogyan rakjuk össze az eredeti kockát a kicsikből, mind a hat szín előfordul a kocka felületén.
Hány részre vágtuk a kockát?

Az 1991. évi
Arany Dániel Matematikai Tanulóverseny
eredménye
Kezdők

A döntőben az ÁLTALÁNOS TANTERVŰ OSZTÁLYOK tanulói 79 dolgozatot adtak be. Az első két feladat hibátlan megoldásáért és a harmadikban elért eredményéért

I. díjat és 1000 Ft jutalmat kapott (betűrendben felsorolva):

Botka Eszter (Szeged, Radnóti M. Kísérleti Gimn. és Ált. Isk. 8. oszt. tanulója, tanára: Vincze István),
Tarján Dénes (Bp., Piarista Gimn., tanára: Lobmayer Imre).

Az első és harmadik feladat hibátlan megoldásáért és a másodikban elért eredményéért

II. díjat és 600 Ft jutalmat kapott:

Timár Ádám (Szeged, Deák F. Gimn., tanára: Horváth Vera).

Az első és második feladat hibátlan megoldásáért és részeredményekért

III. díjat és 350 Ft jutalmat kapott:

Bajszi István (Bonyhád, Petőfi S. Gimn., tanára: Katz Sándor).

I. dicséretben és 100 Ft könyvutalványban részesült:

az első és harmadik feladat jó megoldásáért

Valkó Benedek (5. Helyezett) (Bp., Fazekas M. Főv. Gyak. Ált. Isk. és Gimn. 8. osztályos tanulója, tanára: Köves Judit);

az első feladat jó megoldásáért és a második feladat részben helyes megoldásáért és általánosításáért

Nagy Vilmos (6. helyezett) (Szeged, Radnóti M. Ált. Isk. és Gimn. 8. osztályos tanulója, tanára: Vincze István).

Egy feladat hibátlan megoldásáért és további részeredményekért

II. dicséretben részesültek (7‐10. helyezettek):

Arató Gabriella (Bonyhád, Petőfi S. Gimnázium, tanára: Katz Sándor),
Demetrovics László (Bp., Trefort Á. Gyak. Isk., tanára: Mohay Péter),
Endrődi Csilla (Bp., Szt. István Gimn. és Ált. Isk. 8. osztályos tanulója, tanára: Laczkó László),
Schubert Mihály (Bp., Városmajori Gimn., tanára: Kovács Ildikó).

A döntőben a SZAKKÖZÉPISKOLÁK tanulói 35 dolgozatot adtak be. Mindhárom feladat jó megoldásáért

I. díjat és 1000 Ft jutalmat kapott:

Birszki Bálint (Vác, Ipari Szakközépiskola, tanára: Benedek Ilona).

Az első két feladat hibátlan és a harmadik feladat lényegében jó, de nem teljes megoldásáért

II. díjat és 600 Ft jutalmat kapott:

Koch György (Paks, Energetikai Szakképzési Int., tanára: Árokszállási Eszter).

Két feladat jó megoldásáért és további részeredményért

III. díjat és 350 Ft jutalmat kapott:

Nagy Gábor (Bp., Kolos R. Szakközépiskola, tanára: Pakai Judit).

Egy hibátlan megoldásért és két feladatban lévő lényeget tartalmazó részeredményeiért

I. dicséretben és 100 Ft-os könyvutalványban részesült:

Varga Zsuzsanna (4. helyezett) (Dunaújváros, Rudas L. Közgazd. Szakk., tanára: Kispálné Szívós Éva),
Szűcs Géza (5. helyezett) (Győr, Jedlik Á. Ip. Szakk., tanára: Oross Tiborné),
Csorba Zoltán (6. helyezett) (Békéscsaba, Széchenyi I. Közgazd. Szakk., tanára: Szabó Jánosné).

A döntőben a SPECIÁLIS TANTERVŰ OSZTÁLYOK tanulói 49 dolgozatot adtak be. Mindhárom feladat teljes megoldásáért és általánosító megjegyzésekért

I. díjat és 1000 Ft jutalmat kapott (betűrendben felsorolva):

Csörnyei Marianna (Bp., Fazekas M. Főv. Gyak. Gimn., tanára: Pataki János, Thiry Imréné, Montágh Balázs),
Futó Gábor (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Pataki János, Thiry-Imréné, Montágh Balázs),
Szeidl Ádám (Miskolc, Földes F. Gimn., tanárai: Vass Iván, Veres Pál, Szabó Kálmán).

Mindhárom feladat teljes megoldásáért

II. díjat és 600 Ft. jutalmat kapott,:

Madarassy Pál (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Pataki János, Thiry Imréné, Montágh Balázs).

Két feladat megoldásáért és további részeredményekért

III. díjat és 350 Ft jutalmat kapott (betűrendben felsorolva):

Németh Ákos (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Pataki János, Thiry Imréné, Montágh Balázs),
Németh Tamás (Kaposvár, Táncsics M. Gimn., tanárai: Iharos Csabáné, Kubatov Antal).

Két feladat teljes, ill. lényegében helyes megoldásáért és további részeredményért

I. dicséretet és 100 Ft-os könyvutalványt kapott. (7‐9. helyezett):

György András (Bp., Árpád Gimn., tanárai: Mikusi Imre, Gyimesi Róbert),
Kóczy László (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Pataki János, Thiry Imréné, Montágh Balázs),
Kovács Zoltán (Szeged, Radnóti M. Kís. Gimn., tanárai: Kosztolányi József, Vincze István).

Két feladat teljes, ill. lényegében helyes megoldásáért

II. dicséretet kapott (10‐13. helyezett):

Hertz István (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Pataki János, Thiry Imréné, Montágh Balázs),
Horvai Péter (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Pataki János, Thiry Imréné, Montágh Balázs),
Megyesi Zoltán (Szeged, JATE Ságvári E. Gyak. Gimn., tanárai: Tarcsay Tamás, Dobi János, Pintér Lajos),
Párniczky Benedek (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Pataki János, Thiry Imréné, Montágh Balázs).

HALADÓK

A döntőben a NEM SPECIÁLIS matematikai osztályba járó gimnáziumi tanuló versenyzők 86 dolgozatot adtak be. Mindhárom feladat teljes megoldásáért és további értékes megjegyzésekért, általánosításokért

I. díjban és 800 Ft pénzjutalomban részesültek:

Katz Sándor (Bonyhád, Petőfi S. Gimn., tanára: Katz Sándor),
Maier Norbert Zsombor (Sárospatak, Református Kollégium Gimn., tanára: Erdei Pálné),
Molnár Lajos (Debrecen, KLTE Gyak. Gimn., tanára: Baranyi Béláné).

Három feladat teljes megoldásáért

II. díjban és 500 Ft pénzjutalomban részesültek:

Győry Máté (Debrecen, KLTE Gyak. Gimn., tanára: Bíró Lajos),
Nyúl László (Kecskemét, Katona J. Gimn., tanára: Szabó István).

Három feladat lényegében helyes megoldásáért

III. díjban és 300 Ft pénzjutalomban részesült:

Kovács Gergely (Tata, Eötvös J. Gimn., tanára: Tóth András),
Marton Gábor (Nagykanizsa, Batthyány L. Gimn., tanára: Pintér Ferenc).

Két feladat helyes megoldásáért

I. dicséretben részesült:

Adorján Richárd (Kecskemét, Katona J. Gimn., tanára: Szabó István),
Csergőffy Tibor (Szombathely, Nagy Lajos Gimn., tanára: Takács Zsolt),
Csikai Szabolcs (Kecskemét, Katona J. Gimn., tanára: Szabó István),
Diószeghy Zoltán (Sárospatak, Református Kollégium Gimn., tanára: Bujdos Mária),
Molnár Balázs (Oroszlány, Lengyel J. Gimn., tanára: Baráth Tibor),
Szász Csaba (Mosonmagyaróvár, Kossuth L. Gimn., tanára: Gulyás Ferencné),
Wagner Kornél (Bp., Fazekas M. Főv. Gyak. Gimn., tanára: Orosz Gyula).

Két feladat lényegében helyes megoldásáért, vagy ezzel egyenértékű teljesítményért

II. dicséretben részesült:

Borgulya Gábor (Pécs, Nagy Lajos Gimn., tanára: Györkő Zoltán),
Erdélyi Kinga (Bp., ELTE Apáczai Csere J. Gyak. Gimn., tanára: Pongrácz László),
Goldman Júlia (Békéscsaba, Rózsa F. Gimn., tanára: Bajnok Zoltán),
Kosztopulosz András (Dunaújváros, Széchenyi I. Gimn., tanárai: Székelyi Sándorné, Fábián István),
Nagy Gábor (Salgótarján, Madách I. Gimn., tanára: Kaszás Judit),
Szemán Péter (Bp., ELTE Apáczai Csere J. Gyak. Gimn., tanára: Korányi Erzsébet),
Tegzes Pál (Bp., ELTE Trefort Á. Gyak. Gimn., tanára: Veszprémi Ferenc),
Vaderna Péter (Bp., ELTE Radnóti M. Gyak. Gimn., tanára: Dékány Józsefné),

valamint
Veres Gábor (Balassagyarmat, Balassi B. Gimn., tanára: Fűrész István),

aki speciális matematikai osztályba jár, de adminisztratív tévedésből általános tantervű feladatlapot kapott, így teljesítményét itt értékelte a bizottság.

A döntőben a SZAKKÖZÉPISKOLÁK tanulói 27 dolgozatot adtak be. A bizottság első díjat nem adott ki. Az első feladat lényegében jó, a harmadik feladat jó, és a második feladat kiemelkedően szép megoldásáért

II. díjban és 500 Ft jutalomban részesült:

Borsos László (Debrecen, Mechwart A. Gépip. Szakk., tanára: Fidlerné Vikár Judit),
Németh Róbert (Győr, Hild J. Építőip. Szakk., tanára: Soleczkiné Giczi Katalin,
Peresztegi Tamás (Zalaegerszeg, Ganz Á. Gépip. Szakk., tanára: Pintér László).

A második feladat hiányosan indokolt, az első és harmadik feladat kifogástalan megoldásáért

III. díjban és 300 Ft jutalomban részesült:

Darnóczi Dávid (Nyíregyháza, Vásárhelyi P. ÉVISZ, tanára: Erlich Ferenc).

Két feladat kifogástalan megoldásáért

I. dicséretben részesültek:

Ágoston Gábor (Bp., Hámán K. Közg. Szakk., tanára: Tolnai Gáborné),
Horváth Szilárd (Vác, Ipari Szakk., tanára: Benedek Ilona),
Lakos Kálmán (Bp., Hámán K. Közg. Szakk., tanára: Fazekas József).

A döntőben a SPECIÁLIS TANTERVŰ osztályok tanulói 70 dolgozatot adtak be. Három feladat teljes megoldásáért és valamelyik feladatban nyújtott lényeges többletteljesítményért

I. díjban és 800 Ft jutalomban részesült:

Faragó Gergely (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Kőváry Károly, Pósa Lajos),
Kálmán Tamás (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly).

Három feladat teljes megoldásáért

II. díjban és 500 Ft jutalomban részesült:

Babcsányi Ákos (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly),
Bajusz Péter (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly),
Bencs József (Miskolc, Földes F. Gimn., tanárai: Szabó Kálmán, Pirkó Béla),
Csorba Péter (Győr, Révai M. Gimn., tanárai: Nagy Róbert, Horváth Péter).

Három feladat lényegében teljes megoldásáért

III. díjban és 300 Ft jutalomban részesült:

Németh Krisztián (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly),
Risbjerg Anna (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly).

Két feladat teljes és egy harmadik hiányos megoldásáért

I. dicséretben részesült:

Berkó Levente (Szeged, Radnóti M. Gimn., tanárai: Mike János, Vincze István),
Gefferth András (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly),
Kiss Gábor (Debrecen, Fazekas M. Gimn., tanárai: Csarkó Tibor, Balázs Tivadar, Kántor Sándor),
Tichler Krisztián (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly).

Két feladat teljes megoldásáért

II. dicséretben részesült:

Csermely Zoltán (Szeged, Radnóti M. Gimn., tanárai: Mike János, Vincze István),
Elekes Márton (Bp., Berzsenyi D. Gimn., tanárai: Hubert Györgyné, Urbán János),
Horváth Gábor (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly),
Imreh Csanád (Szeged, JATE Ságvári E. Gyak. Gimn., tanárai: Blázsik Zoltán, Seres Lászlóné),
Kassai Lóránt (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly, Pósa Lajos),
Marx Gábor (Bp., Szent István Gimn., tanárai: Rácz János, Nagy Gyula),
Molnár-Sáska Gábor (Bp., Fazekas M. Főv. Gyak. Gimn., tanárai: Laczkó László, Kőváry Károly, Pósa Lajos),
Németh László (Kaposvár, Táncsics M. Gimn., tanára: Kiss Zoltán),
Szendrei Tamás (Miskolc, Földes F. Gimn., tanárai: Pirkó Béla, Szabó Kálmán).

A versenybizottságok