Kezdőlap


Cím:	1990. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):	Surányi János
Füzet:	1991/február, 51 - 61. oldal	PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Legyen $p$ páratlan prímszám, $n$ pedig pozitív egész. Bizonyítsuk be, hogy $p n^{2}$ -nek legfeljebb egy olyan $d$ pozitív osztója van, amelyikre $d + n^{2}$ négyzetszám.

I. megoldás: A számelmélet alaptétele értelmében

d

prímszámhatványok szorzatára történő felbontásában csak azok a prímszámok szerepelhetnek, amelyek

p n^{2}

felbontásában szerepelnek, és legfeljebb akkora kitevőn, mint az utóbbi felbontásban. Így két esetet különböztethetünk meg. Ha

p

nem szerepel

d

felbontásában, akkor

d

osztója

n^{2}

-nek is, ha pedig szerepel, akkor

d = p d'

, ahol

d'

osztója

n^{2}

-nek.
Feltétel szerint van olyan

m

pozitív egész, amelyre az első esetben

\begin{matrix} d + n^{2} = m^{2}, a másodikban p d' + n^{2} = m^{2} . \end{matrix}

Véve

d

, illetőleg

d'

egy tetszés szerinti

q

prím osztóját, azzal

n^{2}

és

m^{2}

is osztható. Mivel a prímtényezős felbontás lényegében egyértelmű, ez csak úgy lehetséges, ha az alapok is oszthatók

q

-val, és így

n^{2}

és

m^{2}

osztható

q^{2}

-tel.
Ekkor

d

, illetőleg

d'

is osztható

q^{2}

-tel, kivéve a második esetben, ha

q = p

. Az említett eset kivételével tehát egyszerűsíthetünk

q^{2}

-tel, és

\begin{matrix} d^{*} + n'^{2} = m'^{2}, illetőleg p d^{*} + n'^{2} = m'^{2} \end{matrix}

alakú összefüggésekhez jutunk, ahol

d^{*}

osztója

n'^{2}

-nek.
Ha a második esetben

q = p

, akkor is oszthatunk

q^{2}

-tel, csak akkor a fenti első típusú egyenlethez jutunk, ahol

d^{*}

most is osztója lesz

n'^{2}

-nek.
Az eljárást megismételhetjük sorra

d^{*}

minden prím osztójára, és így azt kapjuk, hogy van olyan pozitív egész

n_{1}

és

m_{1}

, amelyekkel fennáll, hogy

\begin{matrix} 1 + n_{1}^{2} = m_{1}^{2} vagy p + n_{1}^{2} = m_{1}^{2} . \end{matrix}

(1)

Az eljárás során minden lépésben

n

egy

q

prím osztójának a négyzetével egyszerűsítettünk, tehát végül is egy olyan

n_{2}^{2}

egésszel, amelyikre

\begin{matrix} n = n_{1} n_{2} és d = n_{2}^{2}, illetőleg d = p n_{2}^{2} . \end{matrix}

Az (1) alatti első egyenlet nem állhat fenn, mert két pozitív négyzetszám különbsége legalább

3

. A második egyenlőségből

\begin{matrix} p = (m_{1} + n_{1}) (m_{1} - n_{1}) . \end{matrix}

Mivel

p

prímszám, így ebből

\begin{matrix} m_{1} + n_{1} = p, m_{1} - n_{1} = 1, tehát 2 n_{1} = p - 1. \end{matrix}

Ezzel azt kaptuk, hogy a feladat feltételei akkor teljesülhetnek, ha

\begin{matrix} n = \frac{1}{2} (p - 1) n_{2} és d = p n_{2}^{2} . \end{matrix}

Ezekre

\begin{matrix} d + n^{2} = {p + {[\frac{1}{2} (p - 1)]}^{2}} n_{2}^{2} = {[\frac{1}{2} (p + 1)]}^{2} n_{2}^{2} = {[\frac{1}{2} (p + 1) n_{2}]}^{2} \end{matrix}

valóban négyzetszám.
Eszerint valóban legfeljebb egy megfelelő

d

van, éspedig akkor van ilyen, ha

n

osztható

\frac{1}{2} (p - 1)

-gyel.

Megjegyzés: Nem használtuk ki a megoldás során, hogy

p

páratlan, viszont

p = 2

esetben az (1) alatti második egyenlőség sem állhat fenn, tehát nincs a feladat feltételeit kielégítő

d

szám. Ennek bizonyítását kívánta az 1953. évi verseny 2. feladata.^{$^{*}$}
Valamivel rövidebb megoldást kapunk, ha felhasználjuk az úgynevezett eukleidészi lemmát, amelyik szerint ha egy szám osztója egy szorzatnak, de relatív prím az egyik tényezőhöz, akkor osztója a másik tényezőnek.

II. megoldás: Feltétel szerint van olyan

k

és

m

egész, amelyekre

\begin{matrix} p n^{2} = d k és d + n^{2} = m^{2} . \end{matrix}

Jelöljük

n

és

m

legnagyobb közös osztóját

d'

-vel. Ekkor

n = d' n', m = d' m'

, ahol

m'

és

n'

egymáshoz relatív prím.
A fenti második egyenlőséget

k

-val végigszorozva és felhasználva az elsőt és az utolsó két egyenlőséget, az előbbi így írható:

\begin{matrix} (p + k) d'^{2} n'^{2} = k d'^{2} m'^{2}, amiből (p + k) n'^{2} = k m'^{2} . \end{matrix}

A prímtényezős felbontás egyértelműsége folytán

m'^{2}

-nek és

n'^{2}

-nek csak olyan prímek lehetnek osztói, és így közös osztói is, amelyek az alapoknak is osztói, ami esetünkben azt jelenti, hogy a két négyzet relatív prím. Az eukleidészi lemma szerint tehát

n'^{2}

, ami osztója a jobb oldalnak, kell, hogy az első tényezőnek legyen osztója. Alkalmas

k'

egésszel tehát

\begin{matrix} k = n'^{2} k' . \end{matrix}

Ezt beírva utolsó egyenlőségünkbe és egyszerűsítve azt kapjuk, hogy

\begin{matrix} p + n'^{2} k' = k' m'^{2}, \end{matrix}

vagy átrendezve

\begin{matrix} p = k' (m'^{2} - n'^{2}) = k' (m' - n') (m' + n') . \end{matrix}

Mivel

p

(pozitív) osztói csak

1

és

p

, így a jobb oldalon egy tényező értéke

p

, a másik kettőé

1

, és mivel az utolsó tényező nagyobb az előtte állónál, így

\begin{matrix} m' + n' = p, k' = m' - n' = 1, tehát n' = \frac{1}{2} (p - 1), n = \frac{1}{2} (p - 1) d' . \end{matrix}

Mindezeket beírva az első feltételi egyenlőségbe és egyszerűsítve azt kapjuk, hogy

\begin{matrix} d = p d'^{2}, \end{matrix}

tehát

p

és

n

meghatározza

d

-t ‐ feltéve, hogy egyáltalán létezik megfelelő

d

; ennek pedig az a feltétele, hogy

n

osztható legyen

\frac{1}{2} (p - 1)

-gyel.

III. megoldás: Legyen

m

olyan egész szám, amelyikre

d + n^{2} = m^{2}

, azaz

\begin{matrix} d = m^{2} - n^{2} = (m + n) (m - n) . \end{matrix}

Jelöljük

m + n

és

m - n

legnagyobb közös osztóját

d'

-vel. Ekkor alkalmas

b

és

c

egészekkel

\begin{matrix} m + n = b d', m - n = c d', \end{matrix}

ahol

b

és

c

relatív prím egymáshoz,

b > c

és

\begin{matrix} d = b c d'^{2}, 2 n = (b - c) d' . \end{matrix}

Az, hogy

d

osztója

p n^{2}

-nek, azt jelenti, hogy van olyan

k

egész, amellyel

\begin{matrix} p n^{2} = d k, \end{matrix}

vagyis

4

-gyel szorozva és a fent találtakat beírva

\begin{matrix} p {(b - c)}^{2} d'^{2} = 4 b c d'^{2} k, amiből p {(b - c)}^{2} = 4 b c k . \end{matrix}

Mivel

b

-nek és

c

-nek nincs

1

-nél nagyobb közös osztója, így

b

-nek és

c

-nek

b - c

-vel sem lehet

1

-nél nagyobb közös osztója. Ekkor azonban mind a kettő

p

-nek kell, hogy osztója legyen, tehát

\begin{matrix} b = p, c = 1, így k = {[\frac{1}{2} (p - 1)]}^{2}, d' = \frac{2 n}{p - 1}; \end{matrix}

ezekből pedig

\begin{matrix} d = p {(\frac{2 n}{p - 1})}^{2} . \end{matrix}

Ezzel azt kaptuk, hogy

p

és

n

már meghatározza

d

-t. Egyben azt is kaptuk, hogy ilyen

d

akkor van, ha

n

\frac{1}{2} (p - 1)

többszöröse.

Megjegyzések: 1. Ha

p = 2

, akkor csak annyi változik, hogy

\frac{1}{2} (p - 1)

nem egész, s így semmilyen

n

-hez nincs megfelelő

d

.
2. Mind a három megoldás módot ad az alkalmas

d

osztók megkeresésére akkor is, ha

p

helyébe tetszés szerinti összetett számot írunk. Ekkor lehet több ilyen

d

is.

2. Az

A B C

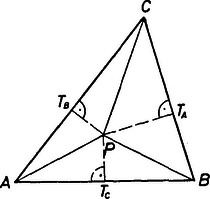
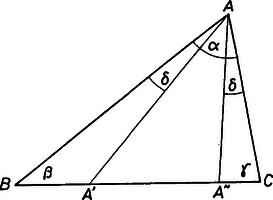
háromszög beírt körének középpontja legyen

K

, a hozzáírt körök középpontjai

A_{0}

B_{0}

C_{0}

. Jelölje

A_{1}

B C

oldal és a

B K C

szög felezőjének,

B_{1}

A C

oldal és az

A K C

szög felezőjének,

C_{1}

pedig az

A B

oldal és az

A K B

szög felezőjének a metszéspontját. Igazoljuk, hogy az

A_{0} A_{1}

B_{0} B_{1}

C_{0} C_{1}

egyenesek egy ponton mennek át.

I. megoldás: A megoldást a következő megjegyzésre építjük. Egy háromszög egy csúcsát a szemközti oldal egy pontjával összekötő szakaszhoz egyértelműen tartozik egy arányszám, amelyikre igaz, hogy egy pont akkor és csak akkor pontja a szakasznak, ha a pont és a szakasszal közös csúcsból induló oldalak távolságainak az aránya az adott érték.

1. ábra

Ha az

A B C

háromszög egy

P

pontjának merőleges vetülete a

B C

C A

és

A B

oldalon rendre

T_{A}

T_{B}

és

T_{C}

(1. ábra), akkor az

A P

B P

C P

egyenesekhez (ill. a háromszögbe eső szakaszaikhoz) tartozó arányok

\begin{matrix} r_{A} = P T_{B} : P T_{C}, r_{B} = P T_{C} : P T_{A}, r_{C} = P T_{A} : P T_{B}, \end{matrix}

és így

\begin{matrix} r_{A} r_{B} r_{C} = 1. \end{matrix}

(2)

Ha fordítva,

P

egy az

A

csúcson és egy a

B

csúcson átmenő egyenes metszéspontja, akkor a két egyeneshez tartozó arány a fenti

r_{A}

és

r_{B}

érték. Ha fennáll (2), akkor

r_{C}

is a fenti érték, s így a

C

ponton átmenő egyenes is átmegy

P

-n.
Más szóval, ha az

A

B

C

csúcson átmenő egy-egy egyenesszakaszhoz tartozó arány

r_{A}

r_{B}

r_{C}

, akkor a szakaszok akkor és csak akkor mennek át egy ponton, ha teljesül (2).

2. ábra

A feladatra térve

A_{0}

B_{0}

C_{0}

a megfelelő külső szögfelezők metszéspontja, így az

A

B

C

csúcsok az

A_{0} B_{0} C_{0}

háromszög oldalaira esnek (2. ábra). Jelöljük az

A B C

háromszög szögeit a szokásos módon

α

β

γ

-val;

A_{1}

merőleges vetületét az

A_{0} B_{0}

A_{0} C_{0}

oldalon

T_{12}

-vel, illetőleg

T_{13}

-mal, és megfelelően a másik két pont vetületeit, amint az ábra mutatja. Ekkor az

A_{0} A_{1}

egyenesre vonatkozó arány az

A_{0} B_{0} C_{0}

háromszögben

\begin{matrix} r_{a} = \frac{A_{1} T_{12}}{A_{1} T_{13}} = \frac{A_{1} C sin B C A_{0}}{A_{1} B sin C B A_{0}} = \frac{A_{1} C cos \frac{γ}{2}}{A_{1} B cos \frac{β}{2}} . \end{matrix}

Hasonlóan

\begin{matrix} r_{B} = \frac{B_{1} A cos \frac{α}{2}}{B_{1} C cos \frac{γ}{2}}, r_{C} = \frac{C_{1} B cos \frac{β}{2}}{C_{1} A cos \frac{α}{2}}, \end{matrix}

és a három arány szorzata

\begin{matrix} \frac{A_{1} C \cdot B_{1} A \cdot C_{1} B}{A_{1} B \cdot B_{1} C \cdot C_{1} A} . \end{matrix}

Tudjuk azonban, hogy a háromszög egy szögének a felezője a szemközti oldalt olyan szakaszokra osztja, amelyeknek az aránya megegyezik a mellettük fekvő oldalak arányával. Ezt egymás után

C K B

A K C

, majd a

B K A

háromszögekre alkalmazva.

\begin{matrix} \frac{A_{1} C}{A_{1} B} = \frac{C K}{B K}, \frac{B_{1} A}{B_{1} C} = \frac{A K}{C K}, \frac{C_{1} B}{C_{1} A} = \frac{B K}{A K} . \end{matrix}

Ezek figyelembevételével azt kapjuk, hogy a fenti szorzat értéke

1

, tehát az előrebocsátott megjegyzés értelmében a három egyenes egy ponton megy keresztül, és ezt kellett bizonyítanunk.

Megjegyzések. 1. A

K

pontról csak annyit használtunk fel, hogy az

A B C

háromszögben van, így a feladat állítása a háromszög bármely

K

pontjára igaz.
2. A bevezető megjegyzésben a háromszög pontjaira szorítkoztunk. Ettől a megszorítástól azonban megszabadulhatunk, ha a háromszög oldalaitól mért távolságot előjelesen értjük: pozitívnak tekintjük azokra a pontokra, amelyek az oldalnak a háromszöget tartalmazó partján vannak, és negatívnak a másik félsík pontjaira. Ekkor csak a háromszög oldalegyeneseit célszerű kizárni.
3. Megvizsgáljuk most a kérdést ennek megfelelően tekintetbe véve az egész síkot. Legyen az

A B C

háromszög

B C

oldalának egy pontja

A'

, merőleges vetülete az

A B

és

A C

oldalon

T_{12}

és

T_{13}

(3. ábra). Ekkor ‐ a háromszög szögeit a szokásos módon jelölve ‐ az

A A'

egyenest jellemző arány

\begin{matrix} r_{A} = \frac{A' T_{12}}{A' T_{13}} = \frac{B A' sin β}{A' C sin γ} . \end{matrix}

3. ábra

B'

és

C'

C A

, illetőleg az

A B

oldal egy-egy pontja, és felírjuk hasonló módon a

B B'

és a

C C'

egyenesre vonatkozó

r_{B}

és

r_{C}

arányt is, akkor a jobb oldalak szorzatában a számlálóban is, a nevezőben is ugyanaz a szinusz-szorzat lép fel, így azzal egyszerűsíthetünk. Azt kapjuk tehát, hogy a (2) bal oldalán álló szorzat a következővel egyenlő:

\begin{matrix} \frac{B A' \cdot C B' \cdot A C'}{A' C \cdot B' A \cdot C' B} . \end{matrix}

(3)

Az is látható, hogy a felírt arányegyenlőségek előjelet tekintve is helyesek maradnak, ha az oldalegyeneseken egy-egy irányt pozitívnak, az ellentéteset negatívnak tekintve előjeles szakaszokkal számolunk, és az egyenesektől mért távolságot is előjelezve értjük a korábban mondott módon. Irányítsuk az oldalegyeneseket például a háromszög óramutatóval ellentétes irányú körüljárásának megfelelően.
Az továbbra is fennáll, hogy ha az

A A'

B B'

C C'

egyenes egy ponton megy keresztül, akkor a (2) szorzat értéke, és így a (3) arányé is 1. A megfordítás helyességének igazolásánál a háromszögben futó két szakasz metszéspontjából indultunk ki. Most azonban felléphetnek párhuzamos egyenesek is.

4. ábra

Ha a három egyenes párhuzamos, válasszuk a betűzést úgy, hogy a

C

csúcs a másik kettőn át húzott párhuzamosok közé essék (4. ábra). Ekkor alkalmazzuk a párhuzamos szelők tételét az

A B A'

és a

B A B'

szögeket átmetsző párhuzamosokra:

\begin{matrix} \frac{B A'}{A' C} = \frac{B A}{A C'}, \frac{C B'}{B' A} = \frac{C' B}{B A} . \end{matrix}

Ezeket a (3) törtbe helyettesítve kapjuk, hogy annak az értéke akkor is

1

, ha a három egyenes párhuzamos.
Megfordítva, ha

A A'

és

B B'

párhuzamos, akkor

C C'

nem metszheti őket, mert ha metszené, akkor korábbi meggondolásunk szerint

B B'

és

C C'

metszéspontján kellene átmennie

A A'

-nek is.
Azt kaptuk tehát, hogy véve az

A B C

háromszög

B C

C A

A B

oldalegyenesének egy-egy, a csúcsoktól különböző

A'

B'

C'

pontját, az

A A'

B B'

és

C C'

egyenesek egy ponton mennek át, vagy párhuzamosak akkor és csak akkor, ha a (3) arány értéke

1

. Ez Ceva tétele. Ezt a versenyzők nagy része ismerte és felhasználta megoldásában.

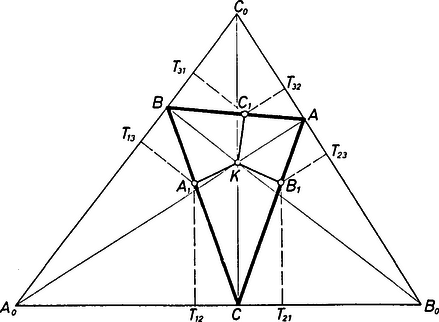
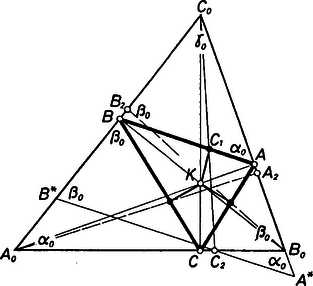
4. Többen ismerték és felhasználták azt is, hogy ha a háromszög egy-egy csúcsán átmenő három egyenes egy ponton megy keresztül, vagy párhuzamosak az egyenesek, és mindegyiket tükrözzük a megfelelő szögfelezőre, akkor a tükrözött egyenesek is vagy egy ponton mennek át, vagy párhuzamosak.

5. ábra

Valóban, legyen

A'

B C

egyenes egy pontja, és messe az

A A'

egyenesnek az

A

csúcsból induló szögfelezőre vonatkozó tükörképe a

B C

egyenest az

A''

pontban. A

B A A' ∢ = δ

jelöléssel, mivel a szögfelezőre tükrözünk,

C A A'' ∢ = δ

(5. ábra). Felhasználva a szinusztételt az

A A' B

A A' C

A A'' B

A A'' C

háromszögekre

\begin{matrix} \frac{B A'}{A' C} = \frac{B A' / A' A}{A' C / A' A} = \frac{sin δ / sin β}{sin (α - δ) / sin γ} = \frac{sin δ sin γ}{sin (α - δ) sin β}, \\ \frac{B A''}{A'' C} = \frac{B A'' / A'' A}{A'' C / A'' A} = \frac{sin (α - δ) / sin β}{sin δ / sin γ} = \frac{sin (α - δ) sin γ}{sin δ sin β} = \frac{A' C sin^{2} γ}{B A' sin^{2} β} . \end{matrix}

Felírva a megfelelő arányokat a

B B'

és a

C C'

tükörképének metszéspontjaként keletkező

B''

és

C''

pontokra is és összeszorozva őket, a számlálóban is, a nevezőben is a háromszög három szöge szinusza négyzetének szorzata keletkezik, így ezzel egyszerűsíthetünk. Azt kapjuk tehát, hogy a kétvesszős pontokra felírt (3)-nak megfelelő kifejezés a vesszős pontokra felírtnak a reciprok értéke. Így Ceva tételéből következik a kimondott állítás helyessége.

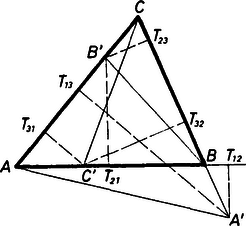
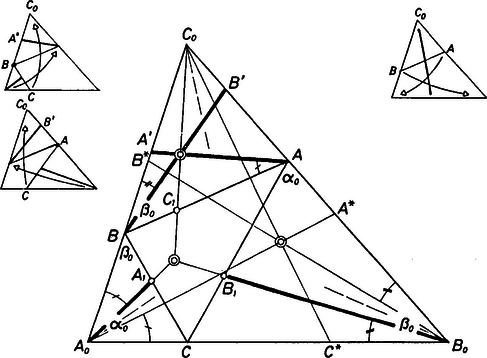
II. megoldás: Jelöljük az

A_{0} B_{0} C_{0}

háromszög szögeit rendre

α_{0}

β_{0}

γ_{0}

-val; az

A_{0} A_{1}

B_{0} B_{1}

C_{0} C_{1}

egyenesnek és az

A_{0} B_{0} C_{0}

háromszög szemközti oldalának a metszéspontját

A_{2}

B_{2}

C_{2}

-vel; húzzunk továbbá

C_{2}

-n át párhuzamost a

B A

egyenessel, messe ez a

C_{0} A_{0}

C_{0} B_{0}

egyenest a

B^{⋆}

, illetőleg

A^{⋆}

pontban (6. ábra).

6. ábra

A háromszöghöz hozzáírt körök középpontjai a háromszög két-két külső és egy belső szögfelezőjének a metszéspontjai, továbbá az egy csúcsból induló belső és külső szögfelező merőleges egymásra, így az

A

B

C

csúcsok az

A_{0} B_{0} C_{0}

háromszög oldalain feküsznek, a háromszög magasságainak talppontjai. Ennek folytán

A_{0} B A B_{0}

húrnégyszög, tehát

\begin{matrix} C_{0} B A ∢ = β_{0}, C_{0} A B ∢ = α_{0}; \end{matrix}

a szerkesztés szerint pedig

\begin{matrix} C_{0} A^{⋆} B^{⋆} ∢ = C_{0} A B ∢ = α_{0}, C_{0} B^{⋆} A^{⋆} ∢ = C_{0} B A ∢ = β_{0} . \end{matrix}

Eszerint

A_{0} B^{⋆} B_{0} A^{⋆}

húrnégyszög, mert

B^{⋆} B_{0}

A_{0}

és az

A^{⋆}

pontból ugyanakkora szögben látszik. Ekkor a

C_{2}

-n átmenő szelők szeleteinek szorzata egyenlő:

\begin{matrix} A_{0} C_{2} \cdot C_{2} B_{0} = B^{⋆} C_{2} \cdot C_{2} A^{⋆} . \end{matrix}

Ez átrendezhető így:

\begin{matrix} \frac{A_{0} C_{2}}{C_{2} B_{0}} = \frac{B^{⋆} C_{2}}{C_{2} A^{⋆}} {(\frac{C_{2} A^{⋆}}{C_{2} B_{0}})}^{2} . \end{matrix}

A jobb oldalt átalakítjuk. A párhuzamos szelők tétele, továbbá a szögfelezőre vonatkozó osztásarányi tétel alapján

\begin{matrix} \frac{B^{⋆} C_{2}}{C_{2} A^{⋆}} = \frac{B C_{1}}{C_{1} A} = \frac{B K}{K A} . \end{matrix}

A második tényezőben az alap így alakítható át, a szinusztételt először az

A^{⋆} B_{0} C_{2}

háromszögre, majd ellenkező irányban az

A_{0} B_{0} C_{0}

háromszögre alkalmazva:

\begin{matrix} \frac{C_{2} A^{⋆}}{C_{2} B_{0}} = \frac{sin (180^{\circ} - β_{0})}{sin α_{0}} = \frac{sin β_{0}}{sin α_{0}} = \frac{C_{0} A_{0}}{C_{0} B_{0}} . \end{matrix}

Ezek szerint

\begin{matrix} \frac{A_{0} C_{2}}{C_{2} B_{0}} = \frac{K B}{K A} {(\frac{C_{0} A_{0}}{C_{0} B_{0}})}^{2} . \end{matrix}

Írjuk fel a megfelelő összefüggéseket

A_{2}

-re és

B_{2}

-re is:

\begin{matrix} \frac{B_{0} A_{2}}{A_{2} C_{0}} = \frac{K C}{K B} {(\frac{A_{0} B_{0}}{A_{0} C_{0}})}^{2}, \frac{C_{0} B_{2}}{B_{2} A_{0}} = \frac{K A}{K C} {(\frac{B_{0} C_{0}}{B_{0} A_{0}})}^{2} . \end{matrix}

A három egyenlőség megfelelő oldalait összeszorozva a jobb oldalon

1

-et kapunk, tehát

\begin{matrix} \frac{A_{0} C_{2}}{C_{2} B_{0}} \cdot \frac{B_{0} A_{2}}{A_{2} C_{0}} \cdot \frac{C_{0} B_{2}}{B_{2} A_{0}} = 1. \end{matrix}

Mivel

A_{1}

B_{1}

C_{1}

A B C

háromszög megfelelő oldalának belső pontja, így az

A_{0} A_{1}

B_{0} B_{1}

C_{0} C_{1}

egyenesek nem lehetnek párhuzamosak, tehát Ceva tétele szerint egy ponton mennek keresztül.

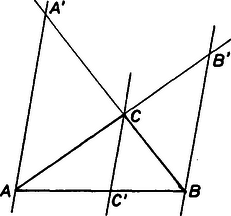
III. megoldás: Az előző megoldás jelöléseit használva az ott követett gondolatmenet ismétlésével kapjuk, hogy

B_{0} A C ∢ = α_{0}

és

A_{0} B C ∢ = β_{0}

. Így az

A_{0} B C

A B_{0} C

A B C_{0}

és

A_{0} B_{0} C_{0}

háromszög hasonló. Az elsőt és a másodikat a harmadikba egy

B

, illetőleg

A

körüli forgatás és ugyanezen középpontú alkalmas hasonlósági transzformáció viszi át, a harmadikat a negyedikbe pedig egy tükrözés a

C_{0}

-ból induló (belső) szögfelezőre és

C_{0}

középpontú hasonlósági transzformáció. Mindezek a transzformációk a szakaszok arányát és a szögek nagyságát változatlanul hagyják.

7. ábra

Vigye át az első és a második transzformáció

A_{0} A_{1}

-et és

B_{0} B_{1}

-et

A A'

-be, illetőleg

B B'

-be (7. ábra). Ekkor

\begin{matrix} \frac{B A'}{A' C_{0}} = \frac{B A_{1}}{A_{1} C}, \frac{C_{0} B'}{B' A} = \frac{C B_{1}}{B_{1} A} . \end{matrix}

A megfelelő oldalakat összeszorozva és szorozva még mindkét oldalt az

A C_{1} / C_{1} B

aránnyal, a jobb oldalon keletkező tört a szögfelezőre vonatkozó osztásarányi tétel szerint

1

lesz, ez pedig Ceva tétele szerint azt jelenti, hogy az

A A'

B B'

és

C_{0} C_{1}

egyenesek egy ponton mennek keresztül.
A föntebb említett harmadik transzformáció ezeket az egyeneseket az ugyancsak egy ponton átmenő

A_{0} A^{⋆}

B_{0} B^{⋆}

C_{0} C^{⋆}

egyenesekbe viszi át. Ezek közül az utolsó egyenes a

C_{0} C_{1}

egyenes tükörképe a

C_{0}

-ból induló szögfelezőre. Hasonló igaz azonban a másik két egyenesre is. Ugyanis a transzformáció például a

B A A'

szöget a

B_{0} A_{0} A^{⋆}

szögbe viszi át, viszont az első transzformáció révén az előbbi szögbe a

B A_{0} A_{1} ∢ = C_{0} A_{0} A_{1} ∢

megy át, ami éppen azt jelenti, hogy

A_{0} A_{1}

és

A_{0} A^{⋆}

egymás tükörképe az

A_{0}

-ból induló szögfelezőre nézve. Hasonlóan okoskodhatunk a harmadik egyenes esetében is. Ekkor azonban

A_{0} A_{1}

B_{0} B_{1}

C_{0} C_{1}

is egy ponton megy keresztül, mint egy ponton átmenő egyeneseknek a megfelelő szögfelezőkre vonatkozó tükörképei.

100

gyerek között egy nem szabályos érme többszöri feldobásával szeretnénk egy ajándékot kisorsolni. A pénzdarabot

k

-szor feldobjuk, miután a dobássorozat minden egyes kimenetelére meghatároztuk, hogy az adott esetben ki nyer.
Bizonyítsuk be, hogy a ,,fej'' dobás

p

valószínűségét és a

k

értékét alkalmasan megválasztva a

2^{k}

kimenetelt fel lehet osztani a gyerekek közt úgy, hogy mindenki egyforma valószínűséggel nyerjen.

I. megoldás: Az alapgondolat az, hogy egy

G

gyereket különválasztva, az azonos számú fejet tartalmazó kimenetelekből annyit, amennyit lehet, egyenletesen szétosztunk a többi gyerek közt, majd a fennmaradó sorozatokat

G

-nek adjuk. Ezután elég

p

-t úgy választani meg, hogy

G

nyerési esélye

1 / 100

legyen, mivel a többi között egyenletesen oszlik meg a maradó

99 / 100

valószínűség. Azt kell bizonyítani, hogy alkalmas

k

esetén ez lehetséges.
Száz gyerek esetén ez kiegészíthető azzal a gondolattal, hogy elég a feladatot száz helyett tízre megoldani. Ha ugyanis tíz gyerek esetén van alkalmas

p

k

és a kimenetelek egy alkalmas szétosztása, akkor a száz gyereket tízes csoportokba osztjuk, és először egy csoportot sorsolunk ki módszerünkkel, majd a csoport tagjai közt sorsoljuk ki az ajándékot.
Jegyezzük még meg, hogy ha valaki a ,,fej''-et tekintené ,,írás''-nak, természetesen akkor is megfelelő maradna az érme, ami azt jelenti, hogy egy

p

értékkel együtt

1 - p

is megoldása a feladatnak. Ez azt sugallja, hogy kényelmesebb

p

-t

\frac{1}{2} - r

alakban keresni; így

1 - p = \frac{1}{2} + r

.
Próbálkozzunk kilenc dobással. Ekkor a

0

1

...

9

fejet tartalmazó dobássorozatok száma sorra

1

9

36

84

126

126

84

36

9

1

. Ezekből az első 9 gyerek közt szétosztva amennyit lehet, csak a

0

, a

3

, a

6

és a

9

fejet tartalmazó sorozatokból marad a tizedik gyereknek rendre

1

3

3

1

. Egy-egy ilyen dobássorozat rendre

{(\frac{1}{2} + r)}^{9}

{{(\frac{1}{2} + r)}^{6} (\frac{1}{2} - r)}^{3}

{(\frac{1}{2} + r)}^{3} {(\frac{1}{2} - r)}^{6}

{(\frac{1}{2} - r)}^{9}

valószínűséggel következik be. Így a következő egyenletet kapjuk:

\begin{matrix} {(\frac{1}{2} - r)}^{9} + 3 {(\frac{1}{2} - r)}^{6} {(\frac{1}{2} + r)}^{3} + 3 {(\frac{1}{2} - r)}^{3} {(\frac{1}{2} + r)}^{6} + {(\frac{1}{2} + r)}^{9} = \frac{1}{10} . \end{matrix}

A bal oldalon

\begin{matrix} {(\frac{1}{2} - r)}^{3} + {(\frac{1}{2} + r)}^{3} = \frac{1}{4} + 3 r^{2} \end{matrix}

köbe áll, így az egyenlet pozitív gyökét keresve azt kapjuk, hogy

\begin{matrix} \frac{1}{4} + 3 r^{2} = \frac{1}{\sqrt[3]{10}}, r = \sqrt[]{(4 - \sqrt[3]{10}) / 12 \sqrt[3]{10}} . \end{matrix}

Innen ‐ 6 értékes tizedesjeggyel számolva ‐ azt kapjuk, hogy a feladat 10 gyerek esetén

k = 9

p = 0, 232 818

választással megoldható.

Megjegyzések: 1. Az első kilenc gyerek egyenként 56 kimenetel esetén nyer, a tizedik összesen 8 esetben, az ezek valamelyike bekövetkezésének a valószínűsége lesz mindegyikük számára egyenlő.
2. A feladat száz gyerek esetén kérdezi az alkalmas dobásszámot és valószínűséget. Erre úgy felelhetünk, hogy mindegyik tízes csoportban előre kiosztjuk azokat a kimeneteleket is, amelyekkel a második fordulóban nyernek, amennyiben az első fordulóból az ő csoportjuk jut tovább. Az egyes gyerekek nyerő kimenetelsorozatai most már úgy adódnak, hogy az első sorozat minden kimeneteléhez hozzáírjuk a második fordulóban rájuk kedvező kimenetelek mindegyikét. Így száz gyerek esetére

p

változatlan,

k = 18

, és lesz, akire

56 \cdot 56 = 3136

kimenetel jut, lesz akire

8 \cdot 56 = 448

, egy gyerekre pedig mindössze

8 \cdot 8 = 64

II. megoldás: Megmutatjuk, hogy a feladat 100 helyett tetszés szerinti

n

-re megoldható a fenti módszerrel. Hagyjuk

k

értékét egyelőre határozatlanul. A

j

fejet tartalmazó sorozatokból az első

n - 1

gyerek mindegyikének ugyanannyit adva, jelöljük

c_{j}

-vel az

n

-edik gyereknek maradó sorozatok számát. Nyilván

c_{0} = c_{k} = 1

. A többi indexre

0 ≦ c_{j} ≦ n - 2

. Mivel egy ilyen sorozat bekövetkezésének a valószínűsége

p^{j} {(1 - p)}^{k - j}

, így a következő egyenletre jutunk:

\begin{matrix} p^{k} + \sum_{j = 1}^{k - 1} c_{j} p^{j} {(1 - p)}^{k - j} + {(1 - p)}^{k} = \frac{1}{n} . \end{matrix}

Belátjuk, hogy ha

k

elég nagy, akkor az egyenletnek van

0

és

1

közé eső megoldása. A bal oldal

p

-nek az egész számegyenesen értelmezett és folytonos

f (p)

függvényét állítja elő, így elég belátni, hogy van olyan hely, ahol

1 / n

-nél nagyobb értéket vesz fel, és olyan is, ahol kisebbet, mert folytonos függvény a két hely között felvesz a két érték közötti minden értéket.

\begin{matrix} f (1) = 1 > \frac{1}{n} . \\ f (\frac{1}{2}) = {(\frac{1}{2})}^{k} (2 + \sum_{j = 1}^{k - 1} c_{j}) \leq {(\frac{1}{2})}^{k} [2 + (k - 1) (n - 2)] \leq {(\frac{1}{2})}^{k} (k - 1) (n - 1), \end{matrix}

k

legalább

3

. Létezik tehát

k

-hoz megfelelő

p

, ha az utolsó kifejezés nem nagyobb, mint

1 / n

, azaz

\begin{matrix} n (n - 1) ≦ \frac{2^{k}}{k - 1} . \end{matrix}

A jobb oldali kifejezés

k

növekedtével minden határon túl nő, tehát minden

n

-hez választható alkalmas

k

és

p

érték.

\begin{matrix} n = 100 esetén 2^{18} / 17 = 262 144 / 17 > 15 420 > 9900, \end{matrix}

tehát választható

p

úgy, hogy 18 dobásból álló sorozattal igazságosan ki lehessen sorsolni az ajándékot.

Megjegyzés. Csak véletlen egyezés, hogy az I. megoldás szerint is 18 feldobással történhet a sorsolás. A II. megoldásnál a

c_{j}

együtthatók kiszámításával belátható, hogy már 16 dobásból álló sorozathoz is van alkalmas

p

érték.

^{$^{*}$}Lásd, Hajós Gy. ‐ Neukomm Gy. ‐ Surányi J.: Matematikai versenytételek II. köt., 3. kiad., Tankönyvkiadó, Budapest, 1988. 157-158.old.