Kezdőlap


Cím:	1991. A XXXII. Nemzetközi Matematikai Diákolimpia feladatainak megoldása
Füzet:	1991/november, 337 - 343. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatok alábbi megoldásait az olimpián részt vett versenyzők készítették.

1. Jelöljük az

A B C

háromszög beírt körének középpontját

I

-vel, a

C B A ∢

A B C ∢

B C A ∢

szögek szögfelezőinek metszéspontját a szemközti oldalakkal pedig rendre

A', B', C'

-vel. Bizonyítsuk be, hogy

\begin{matrix} \frac{1}{4} < \frac{A I \cdot B I \cdot C I}{A A' \cdot B B' \cdot C C'} \leq \frac{8}{27} . \end{matrix}

(USA)

Megoldás. Legyenek az

A B C

háromszög oldalai a szokásos jelöléssel

a, b,

és

c

Segédtétel: Ismert, hogy

\begin{matrix} \frac{A I}{A A'} & = \frac{b + c}{a + b + c}, \\ \frac{B I}{B B'} & = \frac{a + c}{a + b + c} és \\ \frac{C I}{C C'} & = \frac{a + b}{a + b + c} . \end{matrix}

(Ennek bizonyítása két szögfelező tétel segítségével:

B A' = \frac{a c}{b + c}

, így

\begin{matrix} \frac{A I}{I A'} = \frac{A B}{B A'} = \frac{c}{\frac{a c}{b + c}} = \frac{b + c}{a}, \end{matrix}

ahonnan valóban

\begin{matrix} \frac{A I}{A A'} = \frac{b + c}{a + b + c}) . \end{matrix}

A számtani és mértani közepek közötti egyenlőtlenséget használva, és az

\frac{A I}{A A'} + \frac{B I}{B B'} + \frac{C I}{C C'} = 2

összefüggést felismerve kapjuk, hogy

\begin{matrix} \frac{A I}{A A'} \cdot \frac{B I}{B B'} \cdot \frac{C I}{C C'} \leq {(\frac{\frac{A I}{A A'} + \frac{B I}{B B'} + \frac{C I}{C C'}}{3})}^{3} = \frac{8}{27}, \end{matrix}

és egyenlőség csak szabályos háromszögnél áll fenn. Másfelől az

a, b

és

c

számokra teljesül a háromszög-egyenlőtlenség, így

(a + b - c) (a + c - b) (b + c - a) + 4 a b c > 0

.
Ezt beszorozva és rendezve:

\begin{matrix} a^{2} b + a^{2} c + b^{2} a + b^{2} c + c^{2} a + c^{2} b + 2 a b c > a^{3} + b^{3} + c^{3} . \end{matrix}

Mindkét oldalhoz hozzáadva

3 (a^{2} b + a^{2} c + b^{2} a + b^{2} c + c^{2} a + c^{2} b) + 6 a b c

-t, majd szorzattá alakítva kapjuk, hogy

\begin{matrix} 4 (a + b) (b + c) (a + c) > {(a + b + c)}^{3}, \end{matrix}

azaz

\begin{matrix} \frac{A I \cdot B I \cdot C I}{A A' \cdot B B' \cdot C C'} = \frac{(a + b) (b + c) (a + c)}{{(a + b + c)}^{3}} > \frac{1}{4} . \end{matrix}

Ezzel a bizonyítandó két egyenlőtlenséget beláttuk.

Matolcsi Máté

2. Legyen

n > 6

egész szám és

a_{1}

a_{2}

...

a_{k}

az összes olyan természetes szám, amely kisebb

n

-nél és relatív prím

n

-hez. Tegyük fel, hogy

\begin{matrix} a_{2} - a_{1} = a_{3} - a_{2} = ... = a_{k} - a_{k - 1} > 0. \end{matrix}

Bizonyítsuk be, hogy ekkor

n

prímszám, vagy

2

-nek egész kitevős hatványa.
(Románia)

Megoldás. Legyen

a_{2} - a_{1} = a_{3} - a_{2} = ... = a_{k} - a_{k - 1} = d

. Mivel

d > 0

, ezért

a_{1} < a_{2} < ... < a_{k}

. Mivel minden pozitív egész

n

-re

(n - 1, n) = 1

, ezért

a_{k} = n - 1

, továbbá nyilván

a_{1} = 1

I. Legyen először

n

páratlan. Ekkor

(n - 2, n) = 1

. (Ugyanis

x | n

és

x | n - 2

esetén

x | 2

, de

n

páratlan, így

x = 1

, ezért

a_{k - 1} = n - 2

. Így viszont

d = 1

és ekkor minden

n

-nél kisebb pozitív egész relatív prím

n

-hez, azaz

n

-nek nincs nála kisebb valódi osztója; így

n

prím, ahogy a feladat állítja.

II. Legyen most

n

páros, és írjuk fel

n = 2^{α} \cdot n_{1}

alakban, ahol

α \geq 1

és

n_{1}

páratlan.
a) Ha

n_{1} = 1

, akkor

n 2

-hatvány, ahogy állítottuk; ekkor a feltétel nyilván teljesül, hiszen az

a_{i}

-k éppen az

n

-nél kisebb páratlan számok és

d = 2

.
b) Ha

n_{1} = 3

volna, akkor

n > 6

miatt

a_{1} = 1, a_{2} = 5, a_{3} = 7

és

a_{2} - a_{1} \neq a_{3} - a_{2}

, ez pedig lehetetlen.
c) Legyen végül

n_{1} \geq 5

. Megmutatjuk, hogy ekkor

n_{1} - 2

és

n_{1} - 4

szerepel az

a_{i}

-k között. Tegyük fel ugyanis, hogy

x | 2^{α} n_{1}

és

x | n_{1} - 2

. Ekkor

x | 2^{α} n_{1} = 2^{α} (n_{1} - 2) + 2^{α + 1}

miatt

x | 2^{α + 1}

. De

x

páratlan, így

x = 1

, azaz

(n_{1} - 2, 2^{α} n_{1}) = 1

. Hasonlóan

(n_{1} - 4, 2^{α} n_{1}) = 1

. Nyilván

n_{1} - 3

nem szerepel az

a_{i}

-k között, hiszen páros; így

d = 2

. De ekkor

n_{1}

is szerepel az

a_{i}

-k között (az

a_{i}

-k rendre

1,3,5, ..., n_{1} - 2, n_{1}, ...

). Ez viszont ellentmondás, mert

(n_{1}, n) = n_{1} > 1

.
Beláttuk tehát, hogy

n

prím vagy

2

-hatvány, a bizonyítást befejeztük.

Szendrői Balázs

3. Legyen

S = {1,2,3, ...,280}

. Határozzuk meg azt a legkisebb

n

egész számot, amelyre igaz az, hogy

S

minden

n

elemű részhalmaza tartalmaz

5

olyan számot, amelyek páronként relatív prímek.
(Kína)

Megoldás. Válasszuk ki az

S

halmazból a

2

, a

3

, az

5

és a

7

többszöröseit. Ezek közül akárhogyan választunk ki 5 számot, lesz kettő, amelyek ugyanannak a prímnek a többszörösei, tehát nem relatív prímek. Az

S

-ből kiválasztott elemek száma a szita-formula segítségével kiszámolva

216

. Ezért a keresett

n

egész legalább

217

.
Bebizonyítjuk, hogy

n = 217

esetén már teljesül a feltétel. Ehhez vizsgáljuk meg, hogy legfeljebb hány elem lehet

S

-nek egy olyan részhalmazában, amelyben nincs

5

olyan szám, amelyek páronként relatív prímek. A fent megadott

216

elemű halmaz kiválasztásakor elhagytuk a prímek és az

1

közül négy kivételével az összeset, a prímnégyzetek közül is négy kivételével az összeset, és ezeken kívül még hat darab két prím szorzataként felírható számot:

\begin{matrix} 11 \cdot 13 11 \cdot 23 11 \cdot 17 13 \cdot 17 11 \cdot 19 13 \cdot 19 \end{matrix}

Az eredeti feltételnek nem megfelelő bármely halmazban is a prímek és az

1

közül legfeljebb

4

lehet, különben lenne

5

szám, amelyek páronként relatív prímek, így ezek közül legalább annyit el kell hagyni, mint az előző példában. Ugyanez igaz a prímnégyzetekre is. Már csak az kell, hogy ezeken kívül még legalább 6 elemet el kell hagyni. Alább megadok 6 db 5 elemű diszjunkt halmazt, amelyek

S

részhalmazai, prímet és prímnégyzetet nem tartalmaznak, és mindegyikben páronként relatív prímek vannak, tehát mindegyik halmaznak legalább egy elemét el kell hagyni az

S

-ből ahhoz, hogy a feltétel ne teljesüljön.
A halmazok:

\begin{matrix} {2^{3}; 3^{3}; 5 \cdot 23; 7 \cdot 19; 11 \cdot 13} & {2^{6}; 3 \cdot 17; 5^{3}; 7 \cdot 13; 11 \cdot 23} \\ {2^{4}; 3^{4}; 5 \cdot 19; 7 \cdot 23; 11 \cdot 17} & {2^{7}; 3 \cdot 23; 5 \cdot 29; 7 \cdot 11; 13 \cdot 19} \\ {2^{5}; 3^{5}; 5 \cdot 13; 7 \cdot 17; 11 \cdot 19} & {2^{8}; 3 \cdot 19; 5 \cdot 11; 7 \cdot 29; 13 \cdot 17} \end{matrix}

Tehát, ha kiválasztunk

S

-ből egy 217 elemű halmazt, akkor az vagy tartalmaz egyet az előbbi 6 halmazból, vagy tartalmaz 5 prímet, vagy található benne 5 prímnégyzet. Ekkor van benne 5 szám, amelyek páronként relatív prímek. Tehát a keresett

n

szám a 217.
Ujváry-Menyhárt Zoltán

4. Legyen a

G

összefüggő gráf éleinek száma

k

. Bizonyítsuk be, hogy meg lehet az éleket számozni az

1,2,3, ..., k

számokkal úgy, hogy minden olyan csúcs esetén, amelyből legalább két él indul ki, az illető csúcsból kiinduló összes élhez rendelt számok legnagyobb közös osztója

1

[Gráfnak nevezzük csúcsnak nevezett pontok egy halmazát, ahol a két különböző csúcsból álló párok némelyikét élek kötik össze. Bármely két különböző

u, v

csúcs között legfeljebb egy él halad. A

G

gráfot összefüggőnek nevezzük, ha bármely két különböző

x, y

csúcshoz található csúcsoknak egy olyan

x = v_{0}, v_{1}, ..., v_{m} = y

sorozata, hogy minden

u_{i}, v_{i + 1} (0 \leq i < m)

csúcspárt él köt össze.]
(USA)

Megoldás. Úgy fogjuk megszámozni az éleket, hogy már két olyan él is tartozzék minden legalább másodfokú csúcshoz, amelyekre egymáshoz relatív prím számokat írtunk; ez nyilván elegendő a feladatbeli állítás bizonyítására.
Legyenek a gráf legalább másodfokú csúcsai

A_{1}, A_{2}, ..., A_{n}

(ha ilyen csúcs nincsen, akkor triviális az állítás). Mivel a gráf összefüggő, ezért bármely csúcsból bármely csúcsba vezet út a gráfban. Menjünk el

A_{1}

-ből

A_{2}

-be,

A_{2}

-ből

A_{3}

-ba,

..., A_{n - 1}

-ből

A_{n}

-be, végül

A_{n}

-ből

A_{1}

-be a gráf egy-egy tetszőleges élsorozatán keresztül! Így egy olyan utazást teszünk a gráfban, amelynek során minden

A_{i}

-t

(i = 1,2, ..., n)

érintünk és elhagyunk legalább egyszer. Tegyük fel, hogy utazásunk alatt sorra számozzuk az érintett éleket az

1,2, ..., l

számokkal

(1 \leq l \leq k)

‐ azzal a kikötéssel, hogy ha egy élre
a) már írtunk számot, akkor arra új számot már nem írunk.
b) még nem írtunk számot (tehát az utazás során először érintjük), akkor 1-gyel nagyobb számot írunk rá, mint amilyet utoljára használtunk.
Ezek szerint mindig csak az "új'' ‐ addig még nem érintett ‐ élekre kell számot írnunk, és összesen

l

db élt számoztunk meg a

k

db él közül.
Az utazásnál még egy dologra kell ügyelnünk:
Ha valamelyik

A_{i}

csúcsot

(i = 2,3, ..., n)

először érintjük utazásunk során (ez biztosan bekövetkezik minden

i

-re valamikor), akkor

A_{i}

-t másik élén keresztül hagyjuk el, mint amilyenen keresztül megközelítettük; ez megtehető, mert

A_{i}

legalább másodfokú. Mivel az

A_{i}

-ből kiinduló élek egyikét sem érintettük azelőtt, ezért a számozási algoritmus szerint ebben a lépésben

A_{i}

-nek

2

élére

2

szomszédos számot kell írnunk.

Ha utazásunkat és a számozást az előírt módon végezzük, akkor teljesül, hogy
‐ az

A_{1}

-ből kiinduló egyik élre (utazásunk első élére) az

1

-et írjuk,
‐

A_{i}

-ből

(i = 1,2,3, ..., n)

kiindul

2

olyan él, amelyre szomszédos számokat írunk.
Mivel

x

és

y

pozitív egészek relatív prímek egymáshoz, ha

x = 1

vagy

y - x = 1

, ezért a megoldás elején megfogalmazott követelményünk teljesül, vagyis ‐ a fennmaradó

k - l

db élt tetszőlegesen megszámozva az

l + 1, l + 2, ..., k

számokkal ‐ a feladat állítását beláttuk.
Harcos Gergely

5. Legyen

P

A B C

háromszög belső pontja. Bizonyítsuk be, hogy a

P A B ∢

P B C ∢

P C A ∢

szögek közül legalább egy kisebb, vagy egyenlő, mint

30^{\circ}

.
(Franciaország)

Megoldás. Használjuk az ábra jelöléseit.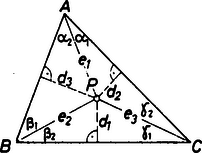

Vegyük észre, hogy

\begin{matrix} \frac{sin α_{1} sin β_{1} sin γ_{1}}{sin α_{2} sin β_{2} sin γ_{2}} = \frac{\frac{d_{2}}{e_{1}} \cdot \frac{d_{3}}{e_{2}} \cdot \frac{d_{1}}{e_{3}}}{\frac{d_{3}}{e_{1}} \cdot \frac{d_{1}}{e_{2}} \cdot \frac{d_{2}}{e_{3}}} = 1. \end{matrix}

Tegyük fel, hogy a feladat állítása nem igaz, tehát

α_{1}, β_{1},

és

γ_{1}

is nagyobb, mint

30^{\circ}

. Ha például

α \geq 150^{\circ}, β

és

γ

is kisebb, mint

30^{\circ}

, így máris ellentmondásra jutottunk. Ha pedig

α, β

és

γ

mindegyike kisebb

150^{\circ}

-nál, akkor

sin α \cdot sin β \cdot sin γ > \frac{1}{8}

. Ugyanakkor a számtani és a mértani közepek közti egyenlőtlenség szerint

\begin{matrix} sin α_{2} sin β_{2} sin γ_{2} \leq {(\frac{sin α_{2} + sin β_{2} + sin γ_{2}}{3})}^{3} . \end{matrix}

A Jensen-egyenlőtlenséget felhasználva (hisz a

sin

függvény a

[0, π]

intervallumon konkáv)

\begin{matrix} sin α_{2} + sin β_{2} + sin γ_{2} \leq 3 sin \frac{α_{2} + β_{2} + γ_{2}}{3} . \end{matrix}

De mivel

0^{\circ} < α_{2} + β_{2} + γ_{2} < 90^{\circ}, 3 sin \frac{α_{2} + β_{2} + γ_{2}}{3} < \frac{3}{2}

, így

\begin{matrix} sin α_{2} sin β_{2} sin γ_{2} < {(\frac{\frac{3}{2}}{3})}^{3} = \frac{1}{8}, \end{matrix}

vagyis

\begin{matrix} \frac{sin α_{1} sin β_{1} sin γ_{1}}{sin α_{2} sin β_{2} sin γ_{2}} > 1. \end{matrix}

Ezzel ellentmondásra jutottunk, tehát bizonyítottuk a feladat állítását.
Kőszegi Botond

6. Valós számok egy

x_{0}, x_{1}, x_{2}, ...

sorozatát korlátosnak nevezzük, ha létezik olyan

C

konstans, hogy

| x_{i} | \leq C

minden

i \geq 0

-ra.
Minden rögzített

a > 1

valós számhoz konstruáljunk olyan korlátos, végtelen

x_{0}, x_{1}, x_{2}, ...

sorozatot, amelyre

\begin{matrix} | x_{i} - x_{j} | | i - j |^{a} \geq 1 \end{matrix}

teljesül bármely két különböző, nemnegatív

i, j

egészre.
(Hollandia)

I. megoldás. Tetszőleges

k \in N

esetén, ha

k

diadikus alakja

\begin{matrix} k = \bar{a_{n} a_{n - 1} ... a_{0}}_{◯ 2} = \sum_{s = 0}^{n} a_{s} \cdot 2^{s} (a_{i} = 0 vagy 1; i = 0, ..., n), \end{matrix}

akkor legyen

\begin{matrix} y_{k} = \sum_{s = 0}^{n} a_{s} \cdot 2^{- a s}, \end{matrix}

ahol

a > 1

a feladatban rögzített valós szám. Legyen most

i, j \in N, i \neq j

, továbbá

i

és

j

kettes számrendszerbeli alakja

\begin{matrix} i = \bar{b_{n} b_{n - 1} ... b_{0}}_{◯ 2} és j = \bar{c_{m} c_{m - 1} ... c_{0}}_{◯ 2} \end{matrix}

Feltehető, hogy

i > j

, és ekkor

n \geq m

. Tegyük fel továbbá, hogy

r

az a természetes szám, amelyre

i

és

j

diadikus alakja az utolsó

r

db jegyben megegyezik, de

(r + 1)

-edik jegyében ‐ hátulról olvasva ‐ már különbözik:

\begin{matrix} r = {min}_{}^{} {s | b_{s} \neq c_{s}, 1 \leq s \leq n}, \end{matrix}

(m < s \leq n

esetén legyen

c_{s} = 0)

. Ekkor

\begin{matrix} | i - j | = i - j \geq 2^{r}, \end{matrix}

(1)

és

a > 1

miatt

\begin{matrix} | y_{i} - y_{j} | & = | \sum_{s = 0}^{n} b_{s} \cdot 2^{- a s} - \sum_{s = 0}^{m} c_{s} \cdot 2^{- a s} | = | \sum_{s = r}^{n} b_{s} \cdot 2^{- a s} - \sum_{s = r}^{n} c_{s} \cdot 2^{- a s} | \geq \\ \geq 2^{- a r} - 2^{- a (r + 1)} - 2^{- a (r + 2)} - ... - 2^{- a n} > 2^{- a r} (1 - \sum_{s = 1}^{\infty} 2^{- a s}) = \\ = 2^{- a r} (1 - 2^{- a} \frac{1}{1 - 2^{- a}}) = 2^{- a r} (1 - \frac{1}{2^{a} - 1}) = 2^{- a r} \cdot \frac{2^{a} - 2}{2^{a} - 1} . \end{matrix}

Ezt

(1)

-gyel egybevetve:

\begin{matrix} | y_{i} - y_{j} | \cdot | i - j |^{a} > 2^{- a r} \cdot \frac{2^{a} - 2}{2^{a} - 1} \cdot {(2^{r})}^{a} = \frac{2^{a} - 2}{2^{a} - 1}, \end{matrix}

ami azt jelenti, hogy az

\begin{matrix} x_{k} = \frac{2^{a} - 1}{2^{a} - 2} y_{k} (k = 0,1, ...) \end{matrix}

sorozat

i, j \in N; i \neq j

esetén

\begin{matrix} | x_{i} - x_{j} | \cdot | i - j |^{a} > 1, \end{matrix}

továbbá

(y_{k})

korlátos volta miatt

(x_{k})

is korlátos:

\begin{matrix} 0 \leq x_{k} = \frac{2^{a} - 1}{2^{a} - 2} y_{k} < \frac{2^{a} - 1}{2^{a} - 2} \cdot \sum_{s = 0}^{\infty} 2^{- a s} = \frac{2^{a}}{2^{a} - 2} . \end{matrix}

Ezzel a feladatot megoldottuk.

II. megoldás. Konstrukciót adunk az

a = 1

esetre ‐ ez nyilván megfelelő

a > 1

esetére is.
Alapötletünk a következő: Tegyük fel, hogy

γ

olyan (irracionális) szám, amelynek minden

\frac{p}{q} (p, q \in Z; q > 0)

közelítő törtjére az eltérés

\begin{matrix} | γ - \frac{p}{q} | \geq \frac{1}{α q^{2}}, \end{matrix}

(2)

ahol

α > 0

valamilyen rögzített konstans. Ekkor tekintjük az

\begin{matrix} x_{k} = α \cdot {γ k} (k = 0,1, ...) \end{matrix}

sorozatot, ahol

{t} = t - [t]

t

szám törtrészét jelöli. Világos, hogy

(x_{k})

korlátos:

\begin{matrix} 0 < x_{k} < α, \end{matrix}

továbbá

i, j \in N; i \neq j

esetén (

i > j

feltehető )

\begin{matrix} | x_{i} - x_{j} | \cdot | i - j | = α \cdot | {γ i} - {γ j} | \cdot | i - j | = \end{matrix}

\begin{matrix}  \end{matrix}

=α⋅|(γi-γj)-([γi]-[γj])|⋅|i-j|,

ill. a

q = i - j (> 0), p = [γ i] - [γ j]

jelöléssel

p

és

q

egészek, tehát (2) szerint

\begin{matrix} | x_{i} - x_{j} | \cdot | i - j | = α \cdot | q γ - p | \cdot q = α q^{2} \cdot | γ - \frac{p}{q} | \geq 1, \end{matrix}

vagyis az

(x_{k})

sorozat megfelelő.
Az is látszik, hogy az

\begin{matrix} x'_{k} = x_{k} - \frac{α}{2} (k = 0,1, ...) sorozatra | x'_{k} | < \frac{α}{2}, továbbá \end{matrix}

\begin{matrix}  \end{matrix}

|x'i-x'j|⋅|i-j|=|xi-xj|⋅|i-j|≥1,

tehát az

x'_{k}

sorozat is megfelelő.
Ezek szerint csak a

(2)

-t kielégítő

γ

-t és

α

-t kell találnunk, sőt minél kisebb az

α

, annál jobb a sorozatunk korlátja.

(2)

-re talán

γ = \sqrt[]{2}

és

α = 3

adja a legegyszerűbb példát:

\begin{matrix} | \sqrt[]{2} - \frac{p}{q} | > \frac{1}{3 q^{2}} \end{matrix}

(3)

mindig fennáll. Ha ugyanis lenne olyan

\frac{p}{q}

közelítő tört, amelyre

\begin{matrix} | \sqrt[]{2} - \frac{p}{q} | \leq \frac{1}{3 q^{2}}, \end{matrix}

(4)

akkor

\begin{matrix} \sqrt[]{2} q - \frac{1}{3 q} \leq p \leq \sqrt[]{2} q + \frac{1}{3 q}, \end{matrix}

azaz négyzetre emelés és rendezés után

\begin{matrix} - \frac{2 \sqrt[]{2}}{3} + {(\frac{1}{3 q})}^{2} \leq p^{2} - 2 q^{2} \leq \frac{2 \sqrt[]{2}}{3} + {(\frac{1}{3 q})}^{2} \end{matrix}

lenne, amiből

\begin{matrix} | p^{2} - 2 q^{2} | \leq \frac{2 \sqrt[]{2}}{3} + {(\frac{1}{3 q})}^{2} \end{matrix}

következnék.

(4)

nyilván nem állhat fenn

q = 1

esetén, ezért

q \geq 2

, tehát

\begin{matrix} | p^{2} - 2 q^{2} | \leq \frac{2 \sqrt[]{2}}{3} + {(\frac{1}{3 \cdot 2})}^{2} = \frac{2 \sqrt[]{2} + \frac{1}{12}}{3} < 1. \end{matrix}

vagyis

\begin{matrix} p^{2} - 2 q^{2} = 0, \end{matrix}

hiszen

| p^{2} - 2 q^{2} |

nemnegatív egész.
Mivel

\sqrt[]{2}

irracionális, ezért

p^{2} - 2 q^{2} = 0

ellentmondást jelent, ami

(3)

-at igazolja.
Ezzel sikerült megadnunk olyan (

x_{k}

) sorozatot, amelyre

\begin{matrix} | x_{k} | < \frac{3}{2}, és | x_{i} - x_{j} | \cdot | i - j | \geq 1 \end{matrix}

teljesül, ha

i, j \in N; i \neq j

.
Harcos Gergely