Kezdőlap


Cím:	Megoldási vázlat az 1991. januári gyakorló felvételi feladatokhoz
Füzet:	1991/február, 64 - 66. oldal	PDF \| MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Az $A B C$ derékszögű háromszög befogói: $A B = 3; B C = 3 \sqrt[]{3}$ ; ezért az átfogó $A C = 6$ , a háromszög köré írt kör sugara $3$ egység. Ezekből következik, hogy az $A O B$ háromszög (amelynek $O$ csúcsa a kör középpontja) egyenlő oldalú: mindegyik oldalának hossza $3$ egység. A körszelet kerülete az $A B$ oldal és az $A B$ ív hosszának összege. Az $A B$ ívhez tartozó középponti szög: $A O B ∢ = 60^{\circ}$ .

\begin{matrix} K_{s z e l e t} = 3 + \frac{2 \cdot 3 π}{6} = 3 + π (= 6, 142) egység. \end{matrix}

A körszelet területét az

A O B

körcikk és az

A O B

egyenlő oldalú háromszög területének különbsége adja:

\begin{matrix} T_{s z e l e t} = \frac{9 π}{6} - \frac{9 \sqrt[]{3}}{4} = \frac{6 π - 9 \sqrt[]{3}}{4} (= 0, 815) területegység. \end{matrix}

2. Felhasználva a

ctg x = \frac{cos x}{sin x}

és a kétszeres szögekre vonatkozó trigonometrikus azonosságokat, az egyenlet

\begin{matrix} \frac{cos x}{sin x} - 2 sin x cos x = \frac{cos x}{sin x} (cos^{2} x - sin^{2} x), \end{matrix}

(1)

x \neq k π (k = 0, \pm 1, \pm 2, ...)

alakra hozható.
Rendezés után az

\begin{matrix} (1 - sin^{2} x - cos^{2} x) cos x = 0 \end{matrix}

(2)

egyenletet kapjuk.
Mivel

1 - sin^{2} x = cos^{2} x

, ezért a szorzat első tényezője nullával egyenlő. Így a (2) egyenlet minden valós számra igaz. Mivel a megadott feltétel mellett egyenértékű átalakításokat végeztünk, az eredeti egyenletnek az

x = k π

-től (

k = 0, \pm 1, \pm 2, ...

) különböző valós számok a megoldásai.

3. A testvérek mostani életkora is egy számtani sorozat négy egymás utáni eleme. Jelölje e sorozat elemeit

a_{1}

;

a_{1} + d

;

a_{1} + 2 d

;

a_{1} + 3 d

, ahol

a_{1}

a legidősebb testvér mostani életkora.
A feltételek szerint

\begin{matrix} {(a_{1} + 2 d - 15)}^{2} = (a_{1} - 15) (a_{1} + 3 d - 15), \\ a_{1} + a_{1} + 2 d + a_{1} + 3 d = \frac{11}{4} (a_{1} + d) . \end{matrix}

Rendezés után a

\begin{matrix} d (4 d - 15 + a_{1}) = 0, \\ a_{1} + 9 d = 0 \end{matrix}

egyenletrendszert kapjuk.
Ha

d = 0

, akkor

a_{1} = 0

, ez azonban nem megoldása a feladatnak. Ha

4 d - 15 + a_{1} = 0

, akkor

d = - 3

és

a_{1} = 27

.
Így a testvérek mostani életkora:

27

;

24

;

21

;

18

év.

4. Az ábra jelölései szerint

A B = 10

, a súlyvonalak

C C_{1} = 6

és

A A_{1} = 9

, továbbá

S

A B C

háromszög súlypontja. Alkalmazzuk a koszinusztételt az

A S C_{1}

háromszögre. Mivel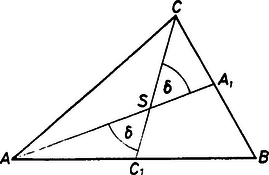

A C_{1} = 5

A S = 6

és

S C_{1} = 2

, ezért

25 = 36 + 4 - 24 cos δ

, és ebből

cos δ = \frac{5}{8}

A_{1} S C

háromszög

C A_{1}

oldalát is a koszinusztétellel számíthatjuk ki: mivel

C S = 4

és

S A_{1} = 3

, ezért

C A_{1}^{2} = 16 + 9 - 24 \cdot \frac{5}{8}

, azaz

C A_{1} = \sqrt[]{10}

. Mivel

2 \cdot C A_{1} = C B

, ezért

C B = 2 \sqrt[]{10} (= 6, 325)

. Az

A S C

háromszögből szintén koszinusztétellel kapjuk meg az

A C

oldal hosszát:

\begin{matrix} A C^{2} = 36 + 16 + 48 \cdot \frac{5}{8} = 82. \end{matrix}

Ebből

A C = \sqrt[]{82} (= 9, 055)

5. Legyen

C (x; y)

az adott kör olyan pontja, amelyre fennáll, hogy

\begin{matrix} \frac{A C}{B C} = \frac{3}{2} . \end{matrix}

(1)

(1)-ből a következő egyenletet kapjuk:

\begin{matrix} 4 [{(x + 4)}^{2} + {(y + 1)}^{2}] = 9 [{(x - 6)}^{2} + {(y - 1)}^{2}] . \end{matrix}

(2)

Mivel

C (x; y)

a kör pontja, ezért (2)-ből és a kör egyenletéből egy egyenletrendszerhez jutunk, amelyből

y = 15 - 5 x

.
Ezt a kör egyenletébe helyettesítve a

13 x^{2} - 76 x + 100 = 0

egyenletet kapjuk. Az egyenlet megoldásai

x_{1} = 2

és

x_{2} = \frac{50}{13}

.
A kör keresett pontjai:

C_{1} (2; 5)

és

C_{2} (\frac{50}{13}; - \frac{55}{13})

6. A csonka kúp tengelymetszetének ábrájáról leolvasható, hogy a csonka kúp alkotója

R + r

, magassága pedig

12

egys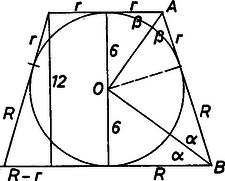ég.

A csonkakúp felszíne:

\begin{matrix} A = π (R^{2} + r^{2}) + π (R + r) (R + r) = 2 π (R^{2} + R r + r^{2}), \end{matrix}

térfogata:

\begin{matrix} V = 4 π (R^{2} + R r + r^{2}) . \end{matrix}

A két mérőszám hányadosa:

\frac{V}{A} = 2

.
A magasság által levágott derékszögű háromszögre Pitagorasz tételét alkalmazva azt kapjuk, hogy

\begin{matrix} 12^{2} + {(R - r)}^{2} = {(R + r)}^{2}, ebből: R r = 36. \end{matrix}

7. Az egyenlet értelmezése miatt

x \neq \pm p

. Az adott egyenlet ekvivalens átalakításokkal

x (4 - p) = 8 p^{2}

alakra hozható. Ha

p = 4

, akkor nincs megoldása az egyenletnek. Ha

p \neq 4

, akkor

x = \frac{8 p^{2}}{4 - p}

. Mivel azonban

x \neq \pm p

, ezért

x = \frac{8 p^{2}}{4 - p} \neq \pm p

.
Az eredeti egyenletnek tehát akkor sincs megoldása,

\begin{matrix} ha \frac{8 p^{2}}{4 - p} = p, azaz p = 0 vagy p = \frac{4}{9}, \\ ha \frac{8 p^{2}}{4 - p} = - p, azaz p = 0 vagy p = - \frac{4}{7} . \end{matrix}

Összefoglalva: Akkor van megoldása az adott egyenletnek, ha

p \neq - \frac{4}{7}; 0; \frac{4}{9}; 4

.
Ahhoz, hogy az egyenlet gyökére teljesüljön a második kérdés feltétele, a

\begin{matrix} \frac{8 p^{2}}{4 - p} < p \end{matrix}

(*)

egyenlőtlenségnek kell fennállnia.
Ha

p < 4

, akkor

(*)

ekvivalens azzal, hogy

9 p^{2} - 4 p < 0

, ami akkor teljesül, ha

0 < p < \frac{4}{9}

.
Ha

p > 4

, akkor

(*)

ekvivalens azzal, hogy

9 p^{2} - 4 > 0

, ez pedig akkor áll fenn, ha

p < 0

vagy

p > \frac{4}{9}

, de a kezdeti feltétel miatt

p > 4

.
Összefoglalva: az egyenlet gyöke akkor lesz kisebb

p

-nél, ha

0 < p < \frac{4}{9}

vagy

p > 4

8. a) Alakítsuk át az adott kifejezést a következő módon:

\begin{matrix} 10^{n} (9 n - 1) + 1 = 9 n \cdot 10^{n} - (10^{n} - 1) = \\ = 9 ({\underset{︸}{10^{n} + 10^{n} + ... + 10^{n})}}_{n tag}^{} - 9 ({\underset{︸}{10^{n - 1} + 10^{n - 2} + ... + 1)}}_{n tag}^{} = \\ = 9 [10^{n - 1} (10 - 1) + 10^{n - 2} (100 - 1) + ... + (10^{n} - 1)] . \end{matrix}

Mivel a szögletes zárójelen belül a kerek zárójeles különbségek mind oszthatók

9

-cel, ezért az egész kifejezés osztható

9 \cdot 9 = 81

-gyel.
b) Mivel

1990 = 10 \cdot 199

, továbbá hogy

10

és

199

relatív prímek, elég bizonyítani, hogy az adott szorzat osztható

199

-cel és

10

-zel.

600^{n} - 3^{n}

osztható

600 - 3 = 597 = 3 \cdot 199

-cel, tehát

199

-cel is.
Azt kell még bizonyítanunk, hogy

n^{5} - n

osztható

10

-zel; ehhez elég megmutatnunk, hogy utolsó jegye

0

. Nézzük végig

n

lehetséges utolsó jegyeit. Ha

n

végződése

0

;

1

;

2

;

...

;

9

, akkor

n^{5}

végződése is rendre

0

;

1

;

2

;

...

;

9

(pl. azért, mert

n^{5}

utolsó jegye rendre megegyezik a

0^{5} = 0

1^{5} = 1

2^{5} = 32

...

9^{5} = 59049

utolsó jegyével), különbségük utolsó jegye tehát valóban

0