Cím: Szabályos tizenhétszög szerkesztése
Szerző(k):  Strommer Gyula 
Füzet: 1991/december, 441 - 449. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. ‐ Gauss* fellépéséig a páratlan oldalszámú szabályos sokszögek közül csak a 3, 5 és 15 oldalú sokszöget tudták körzővel és vonalzóval megszerkeszteni.*  Gauss 1796-ban, 18 éves korában felfedezte, hogy a szabályos 17-szög is megszerkeszthető körzővel és vonalzóval. Ez a felfedezés, melyre egész életében büszke volt,* indította arra, hogy életét a matematika tanulmányozásának szentelje.
Gauss tulajdonképpen csak azt mutatta meg, hogy a szabályos 17-szög szerkesztése négy másodfokú egyenlet gyökeinek a megszerkesztésére vezethető vissza, anélkül, hogy a szerkesztés keresztülvitelére eljárást adott volna. Az azóta eltelt időben a szabályos 17-szög számos különböző szerkesztését közölték. Ezek mind az említett négy egyenlet geometriai megoldásán alapulnak. Nem ismeretes olyan szerkesztés, mely a feladat tiszta geometriai elemzésén alapulna. A következőkben a szabályos 17-szög szerkesztésének egy ilyen tárgyalását adjuk.

 

2. ‐ Jelentsék A, A1, A2, ..., A16 az O középpontú és OA=1 sugarú körbe beírt szabályos 17-szög egymásután következő csúcspontjait. Az A1, A2, ..., A8 pontokból az AB átmérőre bocsátott merőlegesek talppontjai legyenek rendre P1, P2, ..., P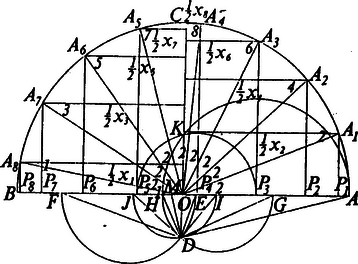8 (1. ábra).
 
 

1. ábra
 


Ugyane pontokból a kör AB-re merőleges OC sugarára bocsátott merőlegesek a körbe beírt szabályos 34-szög egy-egy átlójának felével egyenlők. Legyen ezen átlók hossza nagyságuk csökkenő sorrendjében x1, x2, x3, ..., x8. Ekkor:
2⋅OP1=x2,2⋅OP5=x7,2⋅OP2=x4,2⋅OP6=x5,2⋅OP3=x6,2⋅OP7=x3,2⋅OP4=x8,2⋅OP8=x1.

Ábránkon feltüntettük az egyes szögeknek a körbe beírt szabályos 34-szög egy oldalához tartozó középponti szögre, mint szögegységre vonatkozó mérőszámát. Ama egyenlő szárú háromszögekből, melyeknek alapja x1, x2, ..., x8 és száraik a kör sugarával egyenlők, összeállítható a 2. ábrán látható háromszög, mely egyenlő szárú.*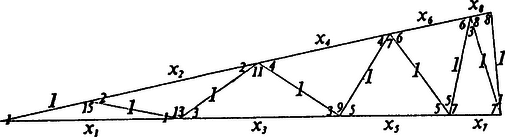

 
 

2. ábra
 

Ebből következik
x1+x3+x5+x7-x2-x4-x6-x8=1
alapegyenletünk.
Ábránk alapján továbbá
1:12x1=x1:(1+12x2),
amiből
x12=2+x2;
hasonlóképpen
1:12x1=x2:12(x1+x3),
amiből
x1x2=x1+x3;
és így tovább. Ily módon a következő szorzótáblát kapjuk:*
x1x2x3x4x5x6x7x8x12+x2x1+x3x2+x4x3+x5x4+x6x5+x7x6+x8x7-x8x2x1+x32+x4x1+x5x2+x6x3+x7x4+x8x5-x8x6-x7x3x2+x4x1+x52+x6x1+x7x2+x8x3-x8x4-x7x5-x6x4x3+x5x2+x6x1+x72+x8x1-x8x2-x7x3-x6x4-x5x5x4+x6x3+x7x2+x8x1-x82-x7x1-x6x2-x5x3-x4x6x5+x7x4+x8x3-x8x2-x7x1-x62-x5x1-x4x2-x3x7x6+x8x5-x8x4-x7x3-x6x2-x5x1-x42-x3x1-x2x8x7-x8x6-x7x5-x6x4-x5x3-x4x2-x3x1-x22-x1

Mármost az x-ekből a következő, különböző tényezőkből álló kéttényezős szorzatok képezhetők:

x1x2,x1x3,x1x4,x1x5,x1x6,x1x7,x1x8;x2x3,x2x4,x2x5,x2x6,x2x7,x2x8;x3x4,x3x5,x3x6,x3x7,x3x8;x4x5,x4x6,x4x7,x4x8;x5x6,x5x7,x5x8;x6x7,x6x8;x7x8.

Ha kiindulunk az x1x2 szorzatból és a szorzótábla segítségével megkeressük azt a két x-et,  melyeknek összege, illetve különbsége e szorzattal egyenlő, azután megkeressük azt a két x-et, melynek összege illetve különbsége az előbb talált két x szorzatával egyenlő, és így tovább, akkor nyolc lépés után az alábbi I. oszlopban felírt egyenlőségeket kapjuk:

I.MMMII.mmmIII.mmmIV.mmmx1x2=x1+x3,x1x4=x3+x5,x1x5=x4+x6,x1x6=x5+x7,x1x3=x2+x4,x3x5=x2+x8,x4x6=x2-x7,x5x7=x2-x5,x2x4=x2+x6,x2x8=x6-x7,x2x7=x5-x8,x2x5=x3+x7,x2x6=x4+x8,x6x7=x1-x4,x5x8=x3-x4,x3x7=x4-x7,x4x8=x4-x5,x3x4=x1+x7,x4x7=x3-x6,x4x5=x1-x8,x1x7=x6+x8,x3x6=x3-x8,x1x8=x7-x8,x6x8=x2-x3,x3x8=x5-x6,x7x8=x1-x2,x2x3=x1+x5,x5x6=x1-x6.

Ha az x1x3, x1x8, x2x4, x2x6, x4x5, x4x8, vagy x7x8 szorzatból indulunk ki, akkor ugyanezeket az egyenlőségeket kapjuk, csak más sorrendben. Ha az I. oszlopban nem szereplő kéttényezős szorzatok közül a szorzatok fent felírt sorában az elsőből, x1x4-ből indulunk ki, akkor a II. oszlopban álló egyenlőségek adódnak. Hasonló módon az eddig nem szerepelt szorzatok közül az elsőből, x1x5-ből kiindulva a III. oszlopban álló egyenlőségeket és az azokban sem szereplő szorzatok közül az elsőből, x1x6-ból kiindulva a IV. oszlopban álló egyenlőségeket kapjuk.
Az egy oszlopban álló egyenlőségek a P pontok által határolt egyenesdarabok fölé, mint átmérő fölé rajzolható nyolc-nyolc, illetőleg négy, egymást meghatározott ciklusos sorrendben követő kör közötti kapcsolatot fejeznek ki, mely szerint az O pontnak bármelyik körre vonatkozó hatványa a rákövetkező kör középpontjának O-tól való távolságával egyenlő. Pl. az x2x6=x4+x8 egyenlőség így is írható:
4⋅OP1⋅OP3=2(OP2+OP4),
vagy még így is:
OP1⋅OP3=12(OP2+OP4);
itt a bal oldalon álló szorzat az O pontnak a P1P3 átmérő fölé írt körre vonatkozó hatványa, a jobb oldalon álló kifejezés pedig a P2P4 átmérő fölé írható kör középpontjának O-tól való távolsága.
Minthogy a II. oszlopban álló egyenlőségekben az O pontnak csak négy körre, a P3P5, P6P7, P1P4, P2P8 fölé, mint átmérő fölé írt körökre vonatkozó hatványa és e körök E, F, G, H középpontjainak O-tól való
OE=12(OP3-OP5)=x6-x7,
OF=12(OP6+OP7)=x3+x5,
OG=12(OP1+OP4)=x2+x8,
OH=12(OP8-OP2)=x1-x4
távolsága közötti kapcsolatot fejeznek ki, mely távolságokra nézve alapegyenletünk is feltételt jelent, törekvésünk arra irányul, hogy e négy kör középpontjai között további olyan kapcsolatot keressünk, amelyek alapján e pontok megszerkeszthetők.
Ha ugyanis e pontokat ismerjük, akkor többféleképpen is meg tudjuk szerkeszteni a keresett sokszöget. Így pl. az
x6x7=x1-x4
egyenletből
OP3⋅OP5=OH=1⋅OH=OA⋅OH,
és így az AH és P3P5 átmérő fölé rajzolt körök az OC sugár egy K pontjában metszik egymást (l. az 1. ábrát). Ha tehát ismerjük az E és H pontokat, akkor meg tudjuk szerkeszteni a P3 és P5 pontokat, és ezek segítségével a keresett sokszöget.
Az E, F, G, H pontok között kapcsolatot keresve mindenek előtt észrevesszük, hogy az EF és GH átmérő fölé írt körök az OC sugár meghosszabbítását ugyanabban a D pontban metszik. Ugyanis:
OE⋅OF=116(x6-x7)(x3+x5)=116(x3x6-x3x7+x5x6-x5x7)=
=116(x3-x8-x4+x7+x1-x6-x2+x5),
és így alapegyenletünk szerint
OE⋅OF=116.

Hasonló módon
OG⋅OH=116(x2+x8)(x1-x4)=116.

Tehát
OE⋅OF=OG⋅OH.

Látni való egyszersmind, hogy
OD=14.

Észrevesszük továbbá, hogy G ugyanolyan arányban osztja az EF távolságot kivülről, mint H belülről. Ugyanis
EG⋅FH=(OG-OE)(OF-OH)=
=116(x2+x8-x6+x7)(x3+x5-x1+x4)=
=116(-x1+x2+x3+x4-x5-x6+x7+x8),
és
FG⋅EH=(OF+OG)(OE+OH)=
=116(x3+x5+x2+x8)(x6-x7+x1-x4)=
=116(-x1+x2+x3+x4-x5-x6+x7+x8),
vagyis
EG⋅FH=FG⋅EH,
amiből
EG:FG=EH:FH.

Minthogy pedig
EDF∢=GDH∢=90∘,
azért
GDE∢=EDH∢=HDF∢=45∘.
Legyen I az AB egyenes ama pontja, mely ugyanolyan arányban osztja az EF távolságot kívülről, mint O belülről. Akkor
OE:OF=EI:FI,
ahonnan
OE⋅FI=OF⋅EI,
vagyis
OE(OF+OI)=OF(OI-OE),
s így
OI=2⋅OF⋅OEOF-OE=(x6-x7)(x3+x5)2(x3+x5-x6+x7),
vagy, mivel
(x6-x7)(x3+x5)=1,
azért
OI=12(x3+x5-x6+x7).

Minthogy pedig EDF∢=90∘, azért EDI∢=ODE∢.
Legyen J az AB egyenes ama pontja, mely ugyanolyan arányban osztja a GH távolságot kívülről, mint az O pont belülről. Akkor
OG:OH=GJ:HJ,
ahonnan
OG⋅HJ=OH⋅GJ,
vagyis
OG(OJ-OH)=OH(OG+OJ),
s így
OJ=2⋅OG⋅OHOG-OH=(x2+x8)(x1-x4)2(x2+x8-x1+x4),
vagy, mivel
(x2+x8)(x1-x4)=1,
azért
OJ=12(x2+x8-x1+x4).

A fentiek szerint
OI⋅OJ=14(x3+x5-x6+x7)(x2+x8-x1+x4),
vagy, mivel
(x3+x5-x6+x7)(x2+x8-x1+x4)=4,
azért
OI⋅OJ=116=OD¯2.

De akkor
OI=116⋅OJ=18(x2+x8-x1+x4)
és
OJ=116⋅OI=18(x3+x5-x6+x7),
s így I a GH és J az EF távolság felezőpontja.
Legyen IJ felezőpontja M. Akkor
OM=116(x3+x5-x6+x7-x2-x8+x1-x4)=116,
és így ADM∢=90∘, mert
OA⋅OM=1⋅OM=116=OD¯2.

Még megjegyezzük, hogy az A pont ugyanolyan arányban osztja az IJ távolságot kívülről, mint az O pont belülről és így ODI∢=IDA∢, tehát
4⋅ODE∢=ODA∢.

Valóban
OJ-OI=18=2⋅OI⋅OJ,
ahonnan
OJ(1-OI)=OI(1+OJ),
vagy
OJ(OA-OI)=OI(OA+OJ),
és így
OJ⋅AI=OI⋅AJ,
azaz
AI:AJ=OI:OJ.

3. ‐ Eredményeink alapján az O középpontú és OA sugarú körbe beírt szabályos 17-szög következő szerkesztése adódik (1. ábra):
A körben megrajzoljuk az AB átmérőre merőleges OC sugarat és a meghosszabbítására rámérjük az OD=14OA távolságot. A D pontban AD-re merőlegest állítunk, mely AB-t M-ben metszi. M-ből, mint középpontból MD sugárral kört rajzolunk, mely OA-t I-ben, OB-t pedig J-ben metszi. BJ meghosszabbítására rámérjük a JE=JD távolságot, AI meghosszabbítására pedig az IH=ID-t. AH fölé, mint átmérő fölé kört rajzolunk, mely OC-t K-ban metszi. Ezután E-ből, mint középpontból a K ponton át kört rajzolunk, mely AB-t P3-ban és P5-ben metszi. E pontokban az AB-re emelt merőlegesek az adott kört a keresett 17-szög A3, A14, és A5, A12 csúcspontjaiban metszik.
Ez a szerkesztés, amint látszik, Lebesque-től67 való, aki a körosztás algebrai elméletéből indul ki.
Meggondolásaink alapján a szabályos 17-szög szerkesztésének egy más módja ‐ mely Richmond-tól8910 való ‐ a következő (1. ábra):
Az OC sugár meghosszabbítására ‐ úgy mint előbb ‐ rámérjük az OD=14OA távolságot. Ezután az OA és OB sugáron meghatározzuk az E és H pontot úgy, hogy EDO∢=14ADO∢ és EDH∢=45∘ legyen. Az E és H pont ismeretében P3 és P5 úgy szerkeszthető meg, mint előbb.
Fenti meggondolásaink alapján a szabályos 17-szög más szerkesztése is könnyen igazolható. Így pl. a következő, talán legismertebb, Serret‐Bachmann-féle11 szerkesztés is (3. ábr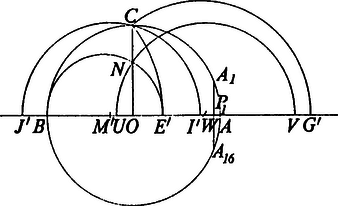a):
 
 

3. ábra
 

Legyen OC az O középpontú kör AB átmérőjére merőleges sugara. Rámérjük a kör OB sugarára az OM'=14OA távolságot és M'-ből, mint középpontból M'C sugárral kört rajzolunk, mely OA-t I'-ben, OB-t pedig J'-ben metszi. J'-ből J'C sugárral körívet rajzolunk, mely AB-t E'-ben metszi; hasonlóképp I'-ből I'C sugárral körívet rajzolunk, mely AB meghosszabbítását G'-ben metszi. BE' fölé félkört rajzolunk, mely OC-t N-ben metszi. E pontból 12OG' sugárral elmetsszük OA-t, miáltal a W pontot kapjuk. Ha a W-ből az N ponton át rajzolt kör AB-t, illetőleg a meghosszabbítását az U és V pontban metszi, akkor OU a körbe beírt szabályos 34-szög oldalhossza, és OV felezőpontja a körbe beírt szabályos 17-szög A-val szomszédos A1 (és A16)csúcspontjából AB-re bocsátott merőleges P1 talppontja.
Valóban,
UV=OG'=4⋅OG=x2+x8
és
OU⋅OV=ON¯2=OB⋅OE'=1⋅OE'=4⋅OE=x6-x7=x2x8,
s így
OU=x8ésOV=x2.
*Carl Friedrich Gaussnémetmatematikus,fizikuséscsillagász,szül.1777.ápr.30-ánBraunschweigben,megh.1855.febr.23-ánGöttingában,ahol1807ótaegyetemitanáréscsillagvizsgálóigazgatójavolt.

*Azutóbbita23  -35=115egyenlőségalapjánakörkerületének3és5egyenlörészrevalóosztásával.

*Erreutalazakívánságais,hogysírkövéreszabályos17-szögetvéssenek.Ezakíváságaugyannemteljesült,deszülővárosábanemeltszobraszabályos17-szögűalaponáll.

*Könnyü belátni, hogy ha n=2k+1, ahol k 1-nél nagyobb egész szám, és φ az egységsugaru körbe beírt 2n oldalu szabályos sokszög egy oldalához tartozó középponti szög, akkor ama egyenlő szárú háromszögekből, melyekben az alapon nyugvó szög φ, 2φ, ..., kφ és száraik egységnyi hosszúságúak, egyenlő szárú háromszög állítható össze. Annak az egyenlő szárú háromszögnek az alapja, amelyben az alapon nyugvó szög kφ, nyilván az egységsugarú körbe beírt szabályos 2n-szög oldalaival egyenlő. Ezt használja fel egy kb. ezer évvel ezelőtt élt névtelen arab szerző és később Vieta francia matematikus is (élt 1540 ‐ 1603) ama algebrai egyenlet levezetésére, amelynek megoldására a körbe beírt szabályos hétszög szerkesztése visszavezethető. (Minthogy ez az egyenlet harmadfokú, a kör sugarából nem állítható elő elemi geometriai szerkesztéssel ‐ azaz pusztán vonalzó és körző használatával ‐ a körbe beírt szabályos hétszög oldalával egyenlő egyenesdarab.)

*A táblázatba foglalt egyenlőségek a π17 szög és többszöröseinek szögfügvényei közötti kapcsolatot fejeznek ki. Pl. Az

x1x2=x1+x3
egyenlőség a
2cosα⋅cosβ=cos(α+β)+cos(α-β)
ismert képletből adódó
2cosπ17⋅cos2π17=cosπ17+cos3π17
összefüggést. Ez teszi lehetővé, hogy további meggondolásainkban a trigonometriát is nélkülözzük.

6Henri Lebesque  (1875‐1941) a CollŠge de France 7tanára és a párizsi tudományos akadémia tagja volt. A fenti szerkesztést Lecons sur les constructions géometriqués című művében találjuk, mely csak halála után, 1950-ben jelent meg Párizsba.

7A CollŠge de France 1530-ban ‐ a hajdani híres, de akkor már hanyatló félben levő párizsi egyetem versenytársaként ‐ a tudományok művelésére és terjesztésére alapított állami intézet, amelyhez mindenkor a legnevesebb tudósokat sikerült megnyerni tanárnak.

8Herbert William Richmond (1863‐1948) a cambridgei King's College-ben9matematikát tanított. A fenti szerkesztést 1893-ban a Quarterly Journal of pure and applied Mathematics 26. kötetében közölte.
Richmond-nál a szerkesztés igazolása azon alapul, hogy a másodfokú egynlet geometriai megoldása ‐ bizonyos feltételek mellett ‐ szögfelezésre vezethető vissza. Például az egységsugarú körbe beírt kétféle szabályos tízszög10oldalhossza kielégíti az

x2+x-1=0
egyenletet, mely még így is írható:
2x1-x2=2.
Ebből a
tgα=2tg12α1-tg212α

ismert képlet alapján ‐ figyelembevéve, hogy fele akkora sugarú körbe beírt szabályos tízszög oldala is fele akkora ‐ a szabályos ötszög következő szerkesztése adódik (4. ábra):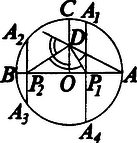
 
 

4. ábra
 


Az O középpontú és OA sugarú kör AB átmérőjére merőleges OC sugarának D középpontját összekötjük A-val; azután megrajzoljuk az ODA szögnek és mellékszögének a felezőjét, mely AB-t P1 és P2 pontban metszi. E pontokban az AB-re emelt merőlegesek a kört a keresett AA1A2A3A4 ötszög A1 és A4, illetőleg A2 és A3 csúcspontjaiban metszik.

9A King's College egyike a cambridge-i egyetemen fennálló 17 intézetnek, amelyekben az egyetem hallgatói a rájuk felügyelő és őket tanító tanárokkal együtt laknak, étkeznek és tanulnak, s amelyeket saját törvényeik szerint igazgatnak.

10Az egységsugarú körbe beírt különböző alakú szabályos n-szögeket úgy kapjuk meg, hogy a kör kerületének kn-ed részéhez tartozó húrt a kerület egy pntjából kiindulva n-szer  egymás útán felrakjuk, ahol k helyébe azokat az n2-nél kisebb pozitív egész számokat tesszük, melyek n-hez relatív prímek.Ha k=1, akkor közönséges szabályos n-szöget kapunk; ha k>1, akkor  a sokszöget szabályos csillag-n-szögnek mondjuk.

11 Joseph Alfred Serret (1819‐1865) a CollŠge de France tanára és a párizsi tudományos akadémia tagja volt. A szabályos 17-szög általa feltalált szerkesztését Cours d'algŠbre supérieure című művében írja le (1849), mely több kiadásban és fordításban jelent meg.
Paul Bachmann (1837‐1920) előbb a boroszlói egyetem, azután a mainzi akadémia tanára volt. A fenti szerkesztés, mely Serret szerkesztésének módosított változata, Die Lehre von der Kreisteilung című művéből való (1872).