|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Ebben a részben elsősorban az -dimenziós konvex poliéderekre vonatkozó Euler-típusú tétel bizonyítása lesz a fő cél. Részben ennek előkészítéseként, részben az eddigiekhez kapcsolódva először modellezzük a 4-, majd később az -dimenziós konvex poliédereket a 3-, illetve általában az -dimenziós térben, valamint megvizsgáljuk az -dimenziós szabályos testeket.
Az előző részben tett erőfeszítéseink ellenére is úgy érzem, csak kissé homályosan tudjuk elképzelni a -dimenziós testeket. Természetesen felmerülő kérdés, hogy lehetséges-e valahogy 3 dimenzióban ábrázolni őket. Nos, abban az értelemben, ahogy a 3-dimenziós testeket le tudjuk rajzolni 2 dimenzióban, eggyel magasabb dimenzióban már gondjaink lesznek. Hiszen egy 2-dimenziós rajzot kívülről, a 3-dimenziós térből nézünk, hasonlóan egy 3-dimenziós rajzot a terünkön kívülről kellene nézni.
Viszont egy 4-dimenziós konvex testnek olyan 3-dimenziós modelljét már el tudjuk készíteni, amelynek a kombinatorikus szerkezete (csúcsok, élek, lapok, hiperlapok száma és kapcsolódása) megegyezik az eredeti testével. Az egyszerűbb érthetőség kedvéért először a 3-dimenziós konvex testeket modellezem a 2-dimenziós síkon.
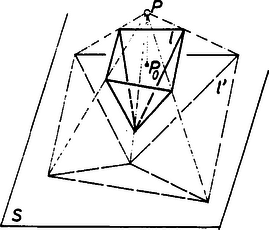
Állítsuk a testet úgy, hogy valamelyik (mondjuk ) lapja fölül, vízszintesen legyen. Vegyünk fel egy vízszintes síkot a test alatt. Legyen -nek egy belső pontja. Mivel a test konvex, ezért a -on átmenő, nem vízszintes egyenesek -on kívül pontosan egy pontban metszik a test felszínét, és a felszín minden, nem -hez tartozó pontjához pontosan egy ilyen egyenes van. Ha elég kicsivel van felett, akkor -re az lesz igaz, hogy minden, belsején áthaladó, -ből induló félegyenes még pontosan egy, -en kívüli pontban metszi a test felszínét, és a felszín minden, -en kívüli pontjához pontosan egy ilyen félegyenes van. Az kerületén átmenő, -ből induló félegyenesek pedig máshol nem metszik a felszínt (1. ábra).
 1. ábra
Vetítsük le a test felszínét -ből a test alatti vízszintes síkra. (Egy felszíni pont vetülete a félegyenes és az sík metszéspontja. Mivel a test felett van, pedig vízszintes, ezért mindig van metszéspont.) Mivel vízszintes volt, ezért vetülete egy -hez hasonló, így konvex sokszög lesz. Az előző bekezdés szerint a felszín -en kívüli részének vetülete egyrétűen lefedi -t. Másrészt a konvex lapok vetületei a lappal megegyező oldalszámú konvex sokszögek, tehát a felszín -en kívüli lapjainak vetületei az konvex sokszöget konvex sokszögekre bontják fel, ezek a konvex sokszögek ugyanolyan típusúak, mint a test lapjai, és a szomszédos lapok vetületei szomszédos sokszögek (2. ábra).
 2. ábra
A kapott konvex tartományrendszernek tehát ugyanolyan a kombinatorikus szerkezete, mint az eredeti konvex poliédernek. A lapú test minden lapjának a vetülete felel meg, így az lapnak , a többi -nek pedig a feldarabolt síkidom darab konvex sokszögtartománya felel meg.
Az így kapott tartományrendszert a test "kifordításának'' fogom hívni. Ezt az elnevezést az motiválja, hogy az előbb kapott tartományrendszert a következőképpen is elő lehet állítani. Képzeljük el, hogy a test felszíne gumihártyából van, az élek gumiszálakból. Tüntessük el az lap hártyáját. Az így kapott lyukat kezdjük kitágítani, és kezdjük el rajta keresztül a testet kifordítani, de ne fordítsuk ki teljesen, csak a lyuk síkjáig. Így egy ugyanolyan kombinatorikus szerkezetű síkbeli tartományrendszert kapunk, mint az előbb, alkalmas nyújtásokkal és összehúzásokkal megkaphatjuk az előző rendszert (3. ábra).
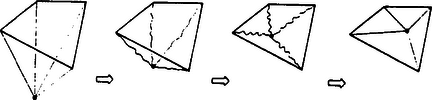 3. ábra
Illusztrációként nézzük meg, hogy mi lesz a 3-dimenziós szabályos testek "kifordítása''. (A "kifordítást'' mindig az első, a vetítős módszerrel fogjuk elvégezni.) Állítsuk a kockát egy vízszintes lapra (erre fogunk vetíteni), legyen a felső lap középpontja fölött kicsivel egy pont. -ből -re vetítve a kockát, az alsó lap fixen marad, a felső lap ezzel párhuzamos élű, nagyobb, koncentrikus négyzetbe jut, a négy oldalsó lapból pedig egy-egy egyenlő szárú trapéz lesz (4.a ábra). A többi szabályos test esetén is úgy érdemes végezni a "kifordítást'', hogy -t a felső lap középpontja felett vesszük, így a 4.b, c, d, e ábrán látható szép szabályos tartományrendszereket kapjuk "kifordításként''.
 4. a ábra
 4. b ábra
 4. c ábra
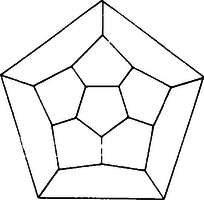 4. d ábra
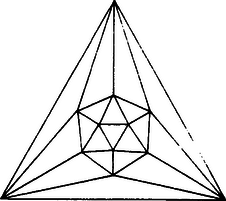 4. e ábra
Ez a "kifordítás'' már 3 dimenzióban is néha igen hasznos, például sok (főként kombinatorikus) tulajdonság sokkal könnyebben vizsgálható a síkbeli modellen. Megfordítva, a 4. ábra rajzait felfoghatjuk gráfoknak is. Így nevezetes síkba rajzolható gráfokat kapunk, amelyeknek néhány tulajdonsága éppen az eredeti test tulajdonságaiból következik.
Minket persze elsősorban a "kifordítás'' többdimenziós általánosítása érdekel. Nézzük először 4 dimenzióban! Legyen egy ( hiperlapú) 4-dimenziós konvex poliéder. Ahogy az egyenes két félsíkra osztja a síkot, a sík két féltérre osztja a teret, a mi -dimenziós terünk két 4-dimenziós féltérre osztja a 4-dimenziós teret. Helyezzük el -t az egyik (mondjuk "felső'') féltérben úgy, hogy az egyik (mondjuk ) hiperlapja párhuzamos legyen a terünkkel, pedig és között legyen. (Azaz a "felső'' hiperlapja.) Legyen nagyon kicsivel egy belső pontja "fölött''. (A "fölött'' precízen azt jelenti, hogy a által meghatározott, -t nem tartalmazó 4-dimenziós féltérben.) -ből vetítsük az testet a terünkre. Ha elég közel volt -hoz, akkor hasonlóan, mint 1-gyel kevesebb dimenzióban, egy hozzá hasonló poliéderbe megy át, a többi hiperlap képe is az eredetivel megegyező kombinatorikus szerkezetű konvex poliéder lesz, ezek ugyanúgy kapcsolódnak, mint az eredetiek, és egy felosztását adják -nek. Vagyis a kapott 3-dimenziós konvex tartományrendszer ugyanolyan kombinatorikus szerkezetű, mint az eredeti 4-dimenziós poliéder.
Készítsük el a I. részben megismert három 4-dimenziós szabályos test "kifordítását''! Ez hasznos lesz, mind a "kifordítás'' megértése, mind a 4-dimenziós testek megismerése szempontjából. Most is kezdjük a legegyszerűbbel, a 4-dimenziós kockával, a tesszerakttal. Legyen az tesszerakt egyik hiperlapja a terünkben, így a "szemközti'' hiperlap párhuzamos a terünkkel, és a tesszerakt a kettő között helyezkedik el. Legyen mondjuk a "felső'' féltérben. Legyen a kocka "fölött'' nagyon kicsivel. Vetítsük a tesszeraktot -ből a terünkre. Hasonlóan, mint 1-gyel kevesebb dimenzióban, önmagába, pedig egy olyan kockába megy át, amely koncentrikus -gyel, tartalmazza -et, lapjai párhuzamosak megfelelő lapjaival. A többi 6 hiperlap képe 6 darab egybevágó, szabályos, négyzet alapú csonkagúla ( ábra).
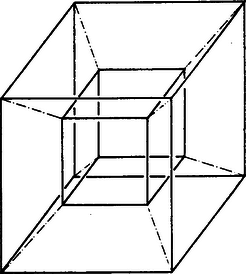 5. a ábra
Ez tehát a tesszerakt 3-dimenziós kombinatorikus modellje. 7 tartománya, 24 lapja, 32 éle és 16 csúcsa van. Ebből is következik, hogy a tesszeraktnak 8 hiperlapja, 24 lapja, 32 éle és 16 csúcsa van. (A hiperlapok száma mindig 1-gyel több, mint a "kifordítás'' tartományainak száma, hiszen az egyik (a ) hiperlap képe nem tartomány, hanem a tartományok egyesítése . Az is jól látszik például a modellből, hogy a csúcsoknál 4 él, 6 lap és 4 hiperlap, az éleknél 3 lap és 3 hiperlap találkozik.
Nézzük a 4-dimenziós szabályos tetraédert. Legyen az egyik csúcsa a terünkben, a szemközti hiperlapja legyen párhuzamos a terünkkel, és maga a test legyen "fölötte''. Legyen nagyon kicsivel középpontja "fölött''. Vetítsük a 4-dimenziós tetraédert -ből a terünkre! önmagába megy, olyan szabályos tetraéderbe, amelynek a középpontja, a másik négy hiperlap képe pedig az ábrán látható módon bontja fel ezt a tetraédert 4 egybevágó kis tetraéderre. ( a közös pontjuk ( 5.b ábra)). A 4-dimenziós szabályos oktaédert kifordítva pedig az 5.c ábrát kapjuk, feltéve, hogy -megint a hiperlap középpontja felett választjuk. Ennek ellenőrzését az olvasóra bízom.
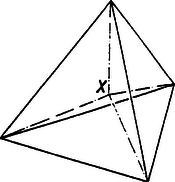 5. b ábra
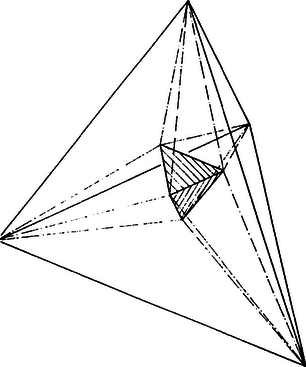 5 c. ábra
A 4-dimenziós eset után már nem nehéz egy -dimenziós konvex poliéder "kifordítását'' definiálni. Legyen -nak egy -dimenziós hiperlapja, legyen egy olyan -val párhuzamos -dimenziós hipersík, amelyre igaz, hogy és között van. Legyen elég kicsivel egy belső pontja "fölött'', azaz a által meghatározott, -t nem tartalmazó féltérben. Vetítsük -ből -t -re. A korábbiakkal analóg módon bizonyítható, hogy ez a vetület -val megegyező kombinatorikus szerkezetű -dimenziós konvex tartományrendszer lesz. Konvex tartományrendszeren egy konvex poliédernek konvex poliéderekre való felosztását értem. A felosztásban szereplő kis poliéderek korlátos tartományok, a tér fennmaradó része alkotja a végtelen tartományt. (A végtelen tartomány nem konvex, viszont a komplementere igen.)
Mielőtt a "kifordítást'' felhasználva belátnánk az -dinenziós Euler-tételt, előbb vizsgáljuk meg az -dimenziós szabályos testeket , és sejtsük meg a tételt! esetén már csak 3 szabályos -dimenziós test van: a szabályos tetraéder, a kocka és a szabályos oktaéder általánosítása. (Ezt nem bizonyítjuk.) Ezeket -re már vizsgáltuk az I. részben, majdnem ugyanúgy megy minden -re is.
Nézzük először az -dimenziós szabályos tetraédert. A 2-, 3- és 4-dimenziós eset analógiájára élű - dimenziós szabályos tetraédernek hívok egy -dimenziós testet, ha , páronként távolságú csúcs, valamint az általuk meghatározott összes -dimenziós él alkotja. (A csúcs -dimenziós él, az él 1-dimenziós él, a lap 2-dimenziós él, az -dimenziós hiperlap -dimenziós él.) A definícióból, rögtön következik, hogy -dimenziós éle van.
Ugyanúgy, ahogy 4 dimenzióban, ebből a definícióból sem látszik, hogy van ilyen test, de ahogy a 4-dimenziós szabályos tetraédert előállítottuk a 3-dimenziósból, az -dimenzióst is elő lehet állítani az -dimenziósból: Vegyünk egy élű -dimenziós szabályos tetraédert, amelynek középpontja . közül bármely kettőnek a távolsága , tehát -et úgy kell megválasztani, hogy hossza is legyen minden -re. Ezt pedig most is úgy lehet megtenni, hogy -ban merőlegest állítunk az -dimenziós térre, és -ból valamelyik irányban felmérünk -t. Így kapjuk -et, ezt összekötve az összes eddigi csúccsal megkapjuk az -dimenziós szabályos tetraédert.
Tehát a szabályos háromszögből kiindulva a fenti lépést -szer végrehajtva megkaphatjuk a szabályos -dimenziós tetraédert. A 4-dimenziós kockára és a 4-dimenziós oktraéderre is volt olyan előállítás az I. részben, amelyik a 3-dimenziós megfelelőből indult ki. Mindkét előállítás szó szerint végrehajtható akkor is, ha -dimenziós testből akarunk -dimenziósat csinálni. Tehát az -dimenziós szabályos tetraéderhez hasonlóan az -dimenziós kockát és az -dimenziós oktaédert is elő lehet állítani rekurzióval lépésben a 2-dimenziós megfelelőjükből, vagyis a négyzetből. Az -dimenzióban is lehet úgy definiálni a szabályos oktraédert, hogy csúcsai az -dimenziós kocka -dimenziós hiperlapjainak középpontjai, a szomszédos hiperlapokhoz tartozó csúcsai közötti szakaszok az élei. A két definíció ekvivalenciáját ugyanúgy kell bizonyítani, mint 4 dimenzióban. A koordináta-rendszerben való szép elhelyezés is szó szerint általánosítható 4 helyett az -dimenziós szabályos testekre.
A vállalkozó kedvűeknek ajánlom, hogy továbbolvasás előtt oldják meg a következő egyszerű feladatot:
Feladat: Határozzuk meg az n-dimenziós kocka és az n-dimenziós oktaéder k-dimenziós éleinek számát
Helyes számolás esetén azt kapjuk, hogy a válasz a feladatra a kocka, és az oktaéder esetén. Tetraéderre már korábban láttuk, hogy a válasz. Jelölje a -dimenziós élek számát. A 3-dimenziós Euler-tétel ezzel a jelöléssel úgy szól, hogy konvex poliéderekre Ha megpróbálunk valami ilyesmit kihozni legalább erre a 3-féle szabályos testre, akkor némi próbálkozás után azt tapasztaljuk, hogy | | (1) |
ezekre a testekre igaz. Ezután már reménykedhetünk benne, hogy esetleg igaz tetszőleges konvex poliéderre. Elárulom, hogy nem hiába reménykedünk, be fogjuk bizonyítani a következő tételt:
Tétel: Minden -dimenziós konvex poliéderre igaz, hogy
| | (1) |
ahol jelöli a -dimenziós élek számát.
Ezt a tételt felfoghatjuk minden egyes -re külön állításként. Adott -re jelöljük ezt az állítást -nel.
A tételt párhuzamosan fogjuk bizonyítani a következő tétellel:
Tétel: Minden -dimenziós konvex tartományrendszerre igaz, hogy:
| | (2) |
ahol a tartományrendszerben lévő -dimenziós élek számát jelöli , , , esetben; pedig a korlátos tartományok számát jelöli.
Ezt a tételt adott -re -nel jelöljük.
A tételek bizonyításához a következőket fogjuk belátni:
igaz.
-ből következik
-ből következik . (Ennek bizonyításakor -t fel fogjuk használni.)
Ez elég, hiszen -ból és -ból következik -re, -ből és -ból pedig következik -re, és ezek együtt jelentik a két bizonyítandó tételt.
A bizonyítások:
: Egy 1-dimenziós konvex tartományrendszer egy szakasz pontokkal felosztva kisebb szakaszokra. Erre nyilván teljesül.
: Vegyünk egy -dimenziós konvex poliédert. Fordítsuk ki! Kapunk egy -dimenziós konvex tartományrendszert. Erre tudjuk, hogy (2) igaz, másrészt hogy a kombinatorikus szerkezete megegyezik az eredeti test kombinatorikus szerkezetével, vagyis | | (3) |
hiszen a korlátos tartományok száma volt, de van egy végtelen tartomány is. (3)-at beírva (2)-be kapjuk (1)-et.
: Ezt az állítást , azaz a korlátos tartományok száma szerinti teljes indukcióval fogjuk bizonyítani.
Nézzük először esetén: azt jelenti, hogy van egy konvex -dimenziós poliéderünk, ami nincs felosztva. -val jelölve a -dimenziós éleinek számát:
| | (4) |
-ből szerint következik , tehát az számokra (1) teljesül. (1)-ből és (4)-ből viszont triviálisan következik (2).
Azt kell még bebizonyítani, hogy esetén igaz az állítás, feltéve, hogy ugyanezt -nél kevesebb korlátos tartomány esetén már tudjuk.
Legyen , és válasszunk ki két szomszédos korlátos tartományt. Mivel ezek konvex poliéderek, ezért egy -dimenziós hipersíkkal szétválaszthatók. (A közös határ hipersíkja ilyen hipersík.) -sel vágjuk ketté az eredeti tartományrendszert. mindkét oldalán kapunk 1‐1 új -dimenziós tartomány-rendszert, jelöljük ezeket -vel, illetve -vel, a -dimenziós éleik számát -val, illetve -val , a korlátos tartományok számát -nel, illetve -nel. A szétvágás során minden korlátos tartományból legfeljebb egy-egy korlátos tartomány keletkezik két oldalán, viszont a két szétválasztott tartomány csak egy-egy oldalra esik, ezért a korlátos tartományok számára teljesül. Ekkor viszont az indukciós feltevés szerint: | | (5) |
| | (6) |
kimetsz -ből egy -dimenziós tartományrendszert. Erre alkalmazva a tételt: | | (7) |
a szokásos jelölésekkel.
Vizsgáljuk meg az tartományrendszert! -nek egy -dimenziós éle, illetve egy korlátos tartománya kétféleképpen keletkezhet: vagy az eredeti -dimenziós -nek is -dimenziós éle volt (ezek számát jelöljük -val), vagy egy egy -dimenziós élének kettévágásakor keletkezett metszetként. Ezek számát jelöljük -val. Nyilván:
| | (8) |
Számítsuk ki -t a , , , és értékekből: Számoljuk össze először csúcsait: -nek van csúcsa egyik oldalán, csúcsa a másik oldalán, csúcs pedig -en, tehát
Számoljuk össze -dimenziós éleit van egyik oldalán, van másik oldalán, van -en. Kétszer számoltuk azokat a -dimenziós éleket, amelyeket kettévág. Viszont éppen az ilyen kettévágásnál keletkezett -dimenziós élek számát jelöltük -gyel, tehát
| | (10) |
korlátos tartományaira továbbá
hiszen van egyik, a másik oldalán, és kétszer számoltuk a darab kettévágott tartományt.
A kapott (5)‐(11) egyenletekből egyszerűen fog adódni a bizonyítandó (2). A (9), (10), (11)-ből:
(5) szerint az első zárójel 1, (6) szerint a második zárójel 1, (7) szerint a harmadik is 1, (8) és (7) szerint az utolsó kettő összege is 1. Tehát: | |
és ezt akartuk bizonyítani. Ezzel -t beláttuk.
Tehát bebizonyítottuk , és -t, és a korábbiak szerint ezekből már következnek a tételeink.
Fel lehet úgy is fogni, hogy -nak komplementere, azaz végtelen tartomány felel meg. A térnek ez a felosztása már teljesen azonos kombinatorikus szerkezetű, mint az eredeti test. |
 PDF | MathML
PDF | MathML