|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A címnek megfelelően nem áll szándékomban valamiféle áttekintést adni a 4-, illetve többdimenziós euklidészi tér geometriájáról, csupán néhány érdekes dologról fogok "mesélni''.
Azt szeretném megmutatni, hogy ez nem valami misztikus, kezelhetetlen világ: egyszerű meggondolásokkal igen meglepő eredményekre lehet jutni, sőt még egy viszonylag "komoly"-nak tűnő tételt is belehet bizonyítani elemi módszerekkel. Gyakorlatilag semmiféle előismeret nem kell, sőt az utolsó résztől eltekintve még bonyolult gondolatmenetekkel sem fogom terhelni az olvasót. Mindössze arra lesz szükség, hogy "merjük'' elképzelni a negyedik és a többi dimenziót. A bizonyításokban, ahol lehet, a szemléletességre fogok törekedni, ez néha a precízség rovására megy. Bemelegítésképpen lássunk be két nagyon egyszerű, de kissé meglepő dolgot a 4-dimenziós térről.
1. Két sík metszete lehet akár egy pont is. Vegyünk fel egy derékszögű koordináta-rendszert; , , és legyenek a tengelyek. Ekkor az , , illetve a , tengelypárok egy-egy síkot határoznak meg. Az elsőn azok a pontok vannak, amelyeknek és koordinátájuk , a másodikon pedig azok, amelyeknek az koordinátájuk , tehát a metszetük a pont, vagyis az origó (1. ábra).
 1. ábra
2. Egy 3-dimenziós balkezes kesztyű átvihető egy háromdimenziós jobbkezes kesztyűbe.
Mielőtt belekezdenénk a bizonyításba, gondoljuk meg, hogy ez az állítás csak nekünk, földhözragadt 3-dimenziós lényeknek meglepő. Egy 2-dimenziós emberkének ugyanekkor meglepetést okozna, ha kivennénk a síkjából a balkezes kesztyűjét, és színével lefelé, jobbkezes kesztyűként tennénk vissza. Pedig hát, 3-dimenziós szemszögből, ebben semmi trükk nem volt.
Könnyen látható, hogy ez a "trükk'' azon múlott, hogy a tér -os, tengely körüli forgatása a tengelyt tartalmazó bármely síkra nézve tengelyes tükrözés (2. ábra).
 2. ábra
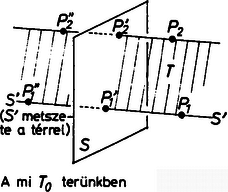
Analóg módon lehet ezt megcsinálni 1 dimenzióval magasabban. Olyan 4-dimenziós mozgatást kell keresni, ami a mi 3-dimenziós terünkben egy síkra való tükrözésnek felel meg. Ez elég lenne, hiszen egy síkra való tükrözés a balkezes kesztyűből jobbkezest csinál. Az analógia azt súgja, hogy a sík körüli -os forgatás megfelelő lesz. Ehhez először meg kell gondolni, hogy mit értsünk egy sík körüli szögű forgatáson. Egy -en kívüli pont képét a következőképpen fogjuk megkapni. Vetítsük merőlegesen -t -re, kapjuk -t. -ben állítsunk merőlegest az és által meghatározott térre. A kapott egyenes és meghatároz egy síkot, amely a -t és -t is tartalmazza. Ezután képét úgy kapjuk, hogy az síkban körül elforgatjuk szöggel (3.a. ábra); pontjai fixek.
 3.a) ábra
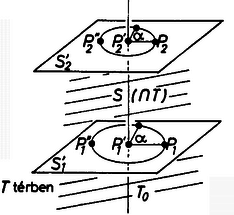
Ellenőrizni kell, hogy a kapott leképezés valóban mozgatás. Ez azon múlik, hogy a definíció alapján egy -re "merőleges'' térben az egyenes körüli szögű forgatás, így minden pont folytonos körpályán mozog, és két pont távolsága is állandó, hiszen az őket tartalmazó, -re merőleges térben egybevágósági transzformáció (3.b. ábra).
 3.b) ábra
Most már csak az kell, hogy az -et tartalmazó térben -re való tükrözés. Ehhez csak a definíciót kell megnézni, a merőleges vetülete. -nek körüli -os forgatása tetszőleges -t tartalmazó síkban úgy is megkapható, hogy a egyenesen -re tükrözöm -t. Így pedig nyilván -nek az -re való tükörképét kapjuk. Ezzel a második állítást bebizonyítottuk.
Játsszunk el a kapott eredménnyel. Balkezes kesztyűt nemcsak úgy lehet felvenni egy ember jobb kezére, hogy a kesztyűt "fordítjuk ki'' , hanem úgy is, hogy a kezet, és vele együtt az embert. Valóban, az eddigiek szerint egy sík körüli forgatás az embert "tükrözi'', a bal és jobb testrészek megcserélődnek.
Ez igen praktikus. Ha valakit zavar, hogy balkezes, semmi probléma, csak el kell forgatni egy sík körül. Ha 1954-ben tudtunk volna sík körül forgatni, akkor lehet, hogy a magyar focicsapat megnyerte volna a világbajnokságot. Ugyanis a döntő előtt a keret összes jobbszélsője megsérült. Így Sebes Gusztáv kénytelen volt egy balszélsőt (Czibor Zoltánt) állítani erre a posztra. (Futballhoz "kevésbé'' értők számára el kell mondani, hogy jobbszélsőnek jobblábasnak kell lennie, a balszélsőnek pedig ballábasnak). Ha a fenti lehetőség rendelkezésünkre állt volna, akkor egy szélső bármelyik szélen tudott volna játszani, így talán több esélyünk lett volna az NSZK legyőzésére, ami így is csak hajszálon múlt...
Gondolatban végezzük el ezt a forgatást egy (3-dimenziós) emberen. Az érdekesség kedvéért legyen az sík egy őt metsző sík. Figyeljük, mi történik: A terünk tetszőleges -en kívüli pontjának a forgási síkja a egyenesben metszi a terünket (a korábbi jelöléseket használva), ezért ezek a pontok a forgatás során nem lesznek láthatóak. (Abból indulok ki, hogy csak a mi 3-dimenziós terünkben lévő dolgokat látjuk.) Az sík pontjai viszont nem mozognak. Vagyis amint elkezdjük forgatni az emberünket, a testének nagy része eltűnik, csak az síkkal való metszete marad előttünk. Egészen a forgatás befejezéséig ezeket a belső részeket látjuk, majd egyszercsak újra megjelenik a teljes ember, akiben remélhetőleg semmi kárt nem tett a ,,4. dimenzió'', mindössze önmaga tükörképe lett.
Az előbbi gondolatkísérletnek (ha valaki nem vette volna észre, ez volt a horror) van egy apró szépséghibája: abból indult ki, hogy egy háromdimenziós testnek nincs kiterjedése a 4. dimenzióban. Ez viszont nem valószínű abban az esetben, ha van 4. dimenzió, és ugyanolyan, mint az első három, pedig ezt feltételeztük. Talán hihetőbb, hogy a "3-dimenziós'' testeknek "kis'' negyedik dimenziós kiterjedése van. Ebben az esetben a forgatás során a metszetnek ezt a "vékony'' burkát fogjuk látni. Ha viszont ez a kiterjedés jelentős és szabálytalan, akkor feltehetően egész furcsa dolgokat láthatunk a forgatott ember "helyén''.
3-dimenziós világunkban sok dolgot lehetetlen megcsinálni, és ezeket ki is használjuk a mindennapi életben. Viszont, amint valaki megtanul 4-dimenzióban mozogni, illetve mozgatni, ezek egy része lehetségessé válik, így nem lehet építeni lehetetlenségükre. Mutatok két példát:
‐ Ki lehet venni tárgyakat egy 3-dimenziós zárt térségből (4-dimenzióban). Ez nagyon egyszerű, ugyanúgy, ahogy egy zárt 2-dimenziós területről úgy kell valamit kivenni, hogy felemeljük a síkról; most a tárgyat a 3-dimenziós térből kell kimozdítani.
‐ Két falhoz rögzített pont közötti csomót ki lehet oldani (lásd 4.a. ábrát).
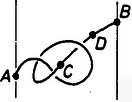 4.a) ábra
 4.b) ábra
 4.c) ábra
Fel fogjuk használni a sík körüli forgatást. Először "emeljük fel'' a kötél egy részét az 4.a. ábrán látható és pontjánál fogva úgy, hogy és kerüljön a legmagasabbra. Ezután a rajtuk átmenő vízszintes sík körül forgassuk el -kal a közötti kötéldarabokat. Ezt megtehetjük, mivel a és nem mozog a forgatás során, vagyis nem fog itt a kötél elszakadni, másrészt a forgás során a és közötti rész a 3-dimenziós terünkön kívül lesz, így nem "akadhat bele'' a többi részbe. Másrészt tudjuk, hogy ez a forgatás a síkra való tükrözésnek felel meg, így a és közötti kötéldarab mindenhol a többi "felett'' fog haladni, vagyis az 4.b. ábrának megfelelő állapotot fogjuk kapni, ez viszont jól láthatóan 3-dimenzióban is könnyen átvihető a 4.c. ábra állapotába, vagyis a csomót kioldottuk.
Ez viszont azt jelenti, hogy ez a csomó 4 dimenzióban nem is csomó. Sőt ehhez hasonlóan a többi bonyolultabb 3-dimenziós csomó sem csomó 4 dimenzióban. De a csomó szerelmeseinek nincs okuk aggodalomra: 4 dimenzióban is van csomó, csak ott nem kötélen van, hanem felületen. Úgy lehet egy ilyet csinálni, hogy az ember fog egy "mezei'' 3-dimenziós csomót, és minden pontjában merőlegest állít a terünkre. A kapott egyenesek (szerintem) egy "felületcsomót'' alkotnak, ennek ellenőrzését az olvasóra bízom.
Az előbb vázolt kibogozási eljárásnál azt feltételeztük, hogy a kötélnek nincs vastagsága. Kérdéses, hogy jó-e ez a módszer igazi spárgák esetében. Sajnos nem! Az egyik lépés során a kötél egy darabját egy sík körül elforgatjuk -kal. Tudjuk, hogy ez a síkra való tükrözésnek felel meg. Nézzük azt az egyik határfelületet, amely egy forgó és egy nyugvó kötéldarabot elválaszt. Ha ennek a felületnek van olyan pontja, ami nincs a forgatási síkon, akkor ott szakadás lesz, hiszen az itt érintkező pontok a sík különböző oldalára kerülnek. Ha viszont a felület a síkban van, akkor a forgatandó kötéldarab egy részének oda kéne kerülnie, ahol a nyugvó rész van (5. ábra).
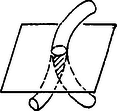 5. ábra
Az utóbbi esetben, ha mégis megpróbálkozunk a forgatással, akkor valószínűleg egy 4-dimenziós kitüremkedés keletkezik, az egy helyre kerülő két darabka közül valamelyik "mindig'' kiszorul a terünkből. Mindenesetre igen furcsa kötelet fogunk kapni.
Mindez persze nem jelenti azt, hogy az igazi csomókat ne lehetne kikötni. Mindössze az eljárást kell egy kicsit módosítani: A forgatásokat ne végezzük el teljesen, azaz -nál kisebb szöggel forgassunk. Ha határfelületnek a síkot választjuk, akkor nincs "szakadás", másrészt "átfedés" sem lehet, hiszen a forgatott rész a terünkön kívül van. (Ennek a mozgatásnak eggyel kevesebb dimenzióban egy papírdarab egyik felének egyenes menti "felhajtása'' felel meg.) A keletkezett 3-dimenziós "lyukon'' keresztül a spárga tetszés szerinti részét átvihetjük. Az elforgatott kötéldarabot visszaforgatva újra 3-dimenziós madzagot kapunk, és ha a megfelelő részt vittük át a "lyukon", akkor most már eggyel kevesebb csomó van a spárgánkon.
Ezt az eljárást folytatva tetszőleges nagy csomó kioldható.
A 4-dimenziós geometria eme néhány "nagyszerű'' alkalmazása után térjünk vissza a "rendes'' matematikához, vizsgáljunk meg néhány szabályos 4-dimenziós testet. Elő fogjuk állítani őket többféleképpen, és ki fogjuk számítani néhány paraméterüket.
Mivel igen körülményes lenne használható definíciót adni arra, hogy mit értsünk általában sokdimenziós poliéderen, illetve speciálisan szabályos (konvex) poliéderen, ezért ettől az egyszerűség kedvéért eltekintek, remélem, hogy ez nem fog gondot okozni.
Kezdjük a vizsgálódást a legegyszerűbb 4-dimenziós szabályos testtel, a 4-dimenziós kockával, szokásos neve tesszerakt. (Általában a 3-dimenziós elnevezéseket használom az általános n-dimenziós fogalmakra, így a hagyományos kocka a 3-dimenziós kocka, a négyzet 2-dimenziós kocka). A 3-dimenziós kockát úgy kaphatjuk meg az élű négyzetből, hogy a síkjára merőleges a hosszúságú vektorral eltoljuk, és a megfelelő csúcsokat összekötjük. Analóg módon definiálhatjuk az élű 4-dimenziós kockát, hogy egy élhosszúságú 3-dimenziós kockát a terére merőleges , hosszúságú vektorral eltoljuk, és a megfelelő csúcsokat összekötjük (6. ábra).
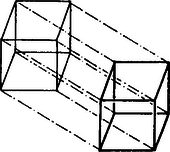 6. ábra
A kapott testnek csúcsa lesz, hiszen a két diszjunkt kocka csúcsai alkotják az ő csúcsait. éle van: e két kocka élei, pedig a csúcspár összekötésénél keletkezett. A tesszerakt lapjai egyrészt a két kocka lapjai, ez , és a megfelelő élpárok között feszülő lapok, ami még , hiszen éle van egy kockának. Tehát lapja van, és ezek élü négyzetek.
Egy 4-dimenziós testet 3-dimenziós térrészek határolnak, ezeket hiperlapnak nevezik. (Általában n-dimenzióban "hipervalamin'' a "valami'' -dimenziós általánosítását szokták érteni, ahol a "valami'' 2-dimenziós fogalom.) A tesszeraktot határolja a két "alapkockánk'', valamint az ezek megfelelő lapjai között feszülő hiperlap, amelyek szintén kockák, vagyis kocka hiperlapja van.
Tehát az élhosszúságú 4-dimenziós kockának csúcsa van, hosszúságú éle, élű négyzet lapja és élű kocka hiperlapja. Méltó a "szabályos test'' névre.
A élhosszúságú tesszerakt igen egyszerűen elhelyezhető a 4-dimenziós derékszögű koordináta-rendszerben is. Induljunk ki a csúcsok által meghatározott 3-dimenziós kockából. A definíció szerint ebből úgy kapunk 4-dimenziós kockát, hogy eltoljuk a vektorral, és a megfelelő csúcsokat összekötjük. Így a kapott 4-dimenziós kocka csúcsai a koordinátájú pontok. Azon pontpárok alkotnak élt, amelyeknek 3 koordinátájuk egyezik meg, négy pont akkor alkot lapot, ha , pont pedig akkor alkot hiperlapot, ha koordinátájuk megegyezik. Innen is könnyen adódnak az előbb kapott eredmények.
A következő szabályos test a 4-dimenziós tetraéder. A 2- és a 3-dimenziós szabályos tetraédert , illetve , páronként egyenlő távolságban lévő csúcs, valamint az általuk meghatározott összes él (és esetleg lap) alkotja. Ezek alapján élű 4-dimenziós szabályos tetraédernek nevezünk egy 4-dimenziós testet, ha , páronként távolságú csúcs, valamint az általuk meghatározott összes él, lap, valamint hiperlap alkotja. Ebből a definícióból rögtön következik, hogy csúcsa, éle, lapja és hiperlapja van, hiszen ennyiféleképpen lehet kiválasztani , illetve csúcsot. Viszont nem látszik a definícióból, hogy létezik ilyen test. A létezést úgy fogom bizonyítani, hogy előállítom, és az előállítás során azt is megmutatom, hogy lényegében csak egyféle ilyen test van.
pont mindig egy 3-dimenziós térben van, ezért csak úgy lehet pont páronként távolságban, ha közülük tetszőleges szabályos élű tetraédert alkot. Vegyünk tehát egy élű szabályos 3-dimenziós tetraédert: csúcsai , középpontja .
Legyen tetszőleges pont a 4-dimenziós térben, a merőleges vetülete az pontok 3-dimenziós terére. Pitagorasz tétele szerint . Tehát ahhoz, hogy minden egyenlő legyen, az kell, hogy minden egyenlő legyen, vagyis legyen. És ez elég is, pedig pontosan akkor teljesül, ha ezenkívül . (Nyilván .)
Tehát az ötödik csúcsot csak úgy kaphatjuk meg, ha -ban merőlegest állítunk terére, majd az egyenesre valamelyik irányban felmérjük a szakaszt, másrészt az így kapott pontot összekötve az csúcsokkal, szabályos 4-dimenziós tetraédert kapunk(7. ábra).
 7. ábra
A 4-dimenziós szabályos tetraédert is el lehet szépen helyezni derékszögű koordináta-rendszerben, de ez valamivel trükkösebb, ugyanis igazán szépen csak az 5-dimenziós koordinátarendszerben lehet elhelyezni. Legyen az csúcs: , , , . Ezek az egyenletű 4-dimenziós hipersíkban vannak, másrészt bármely kettő távolsága Pitagorasz tétele szerint , tehát ők, és az általuk meghatározott élek, lapok, hiperlapok 4-dimenziós, élű szabályos tetraédert alkotnak.
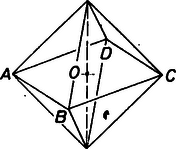
A harmadik, és szerintem legérdekesebb szabályos test amivel foglalkozni fogunk, az oktaéder 4-dimenziós megfelelője. A 3-dimenziós oktaéder egyik definíciója az, hogy csúcsai a kocka lapközéppontjai, a szomszédos lapokhoz tartozó csúcsok közötti szakaszok az élei, az egy pontban érintkező lapokhoz tartozó csúcsok által alkotott háromszögek az oktaéder lapjai (8. ábra).
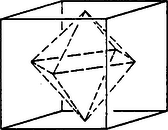 8. ábra
Analóg módon definiálom a 4-dimenziós oktaédert (amit egyéni rövidítésként noktaédernek is nevezek), legyenek csúcsai a tesszerakt hiperlap középpontjai, a szomszédos hiperlapokhoz tartozó csúcsok közötti szakaszok az élei. Az így kapott háromszögek a lapjai, a kapott tetraéderek a hiperlapjai. E definíció szerint annyi csúcsa van, ahány hiperlapja a tesszeraktnak; annyi éle, ahány lapja van a tesszeraktnak, hiszen a tesszerakt minden lapját egy noktaéder él metszi át; annyi lapja, illetve hiperlapja van, mint ahány éle, illetve csúcsa van a tesszeraktnak, hiszen a tesszerakt egy-egy élét, illetve csúcsát veszi körül a noktaéder egy-egy lapja, illetve hiperlapja.
Tehát a csúcsok, élek, lapok, illetve hiperlapok száma rendre: .
A fenti definícióból a szabályosság is látszik, viszont nem érződik a "testszerűsége'', valamint elképzelni sem nagyon lehet. Adódni fog egy olyan meghatározás, amelyik e két utóbbi feltételnek is megfelel. Először azonban helyezzük el a noktaédert a 4-dimenziós derékszögű koordináta-rendszerben:
Vegyük a csúcsok által meghatározott tesszeraktot. Ennek egyik hiperlapja az csúcsok alkotta kocka, amelynek középpontja, így a tesszerakt egyik csúcsa az pont. Ugyanúgy előállítva a többi csúcsot is a , , , csúcsokat kapjuk. Két csúcs akkor van összekötve, ha szomszédos kockák középpontja, azaz a nem koordinátájuk máshol van (9. ábra).
 9. ábra
 10. ábra
Hagyjuk el a csúcsokat, és az ezekbe befutó éleket. Vegyük észre hogy a maradék csúcs a egyenletű 3-dimenziós térben van, és a megmaradt, élekkel együtt egy szabályos oktaédert alkot (10. ábra). Másrészt a kihagyott két csúcs egymással nincs összekötve, de az oktaéder összes csúcsával össze van kötve. Ezek alapján már könnyű a noktaédert szemléletesen is megadni.
Vegyünk egy sugarú gömbbe írt szabályos oktaédert. Vegyünk 1-1 pontot, "alatta'', illetve "fölötte'', azaz a középpontjában állítsunk merőlegest a terünkre, mindkét irányban mérjük fel az egységet. (A 11. ábrán csak az egyik irányt rajzoltuk.) A kapott új csúcsot kössük össze az oktaéder csúcsaival. Így a hiperlap az oktaéder 8 lapjára állított 2‐2 szabályos tetraéder lesz. (Természetesen 1 helyett tetszőleges méretben is csinálhatjuk ezt.)
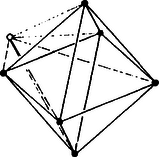 11. ábra
 12. ábra
Ennek az előállításnak számos érdekessége van. Az egyik, hogy ez is analóg a 3-dimenziós szabályos oktaéder egyik előállításával. A szabályos oktaéder egyik legszemléletesebb előállítása az, hogy egy négyzet csúcsait összekötjük középpontja alatt, illetve fölött megfelelő távolságban elhelyezett 1‐1 csúccsal (12. ábra). Első pillantásra kissé sántít ez az analógia, hiszen a négyzet 3-dimenziós megfelelője a kocka. De nemcsak az! Ugyanis a négyzet nemcsak 2-dimenziós kocka, hanem 2-dimenziós oktaéder is.
Ahogy 3- és 4-dimenzióban a megfelelő dimenziós kockák hiperlapjainak középpontjai alkotják a szabályos oktaédert, úgy 2. dimenzióban a négyzet hiperlap középpontjai, vagyis az élfelezőpontok, azok pedig négyzetet alkotnak (13. ábra).
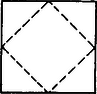 13. ábra
Tehát nem úgy kapunk szabályos n-dimenziós oktaédert, hogy egy -dimenziós kockához veszünk "alatta'' és "felette'' 1‐1 pontot, hanem alapján úgy tűnik, hogy -dimenziós oktaéderrel kell ezt megcsinálni.
Az előbbi előállításból viszont már 3 dimenzióban sem igen látszik a szabályosság, hiszen két egymásra helyezett gúlát képzelünk el. Igen furcsa, hogy ha ezt a gúlát -kal elforgatjuk, akkor semmi sem változik, az oktaéder ugyanúgy fog állni. Persze máshogy fog elhelyezkedni benne a két gúla. Ez 4 dimenzióban még furcsább. Hiszen azt kaptuk, hogy bizonyos 4 különböző (egymásra merőleges) 3-dimenziós térben véve adott méretű szabályos oktaédert, majd megfelelő távolságban "alatta'' és "fölötte'' 1‐1 pontot, mind a 4 esetben "személyesen'' ugyanazt a noktaédert kapjuk.
Még egy érdekesség. Egy oktaéderből indultunk ki, a kapott 4-dimenziós testnek viszont nincs oktaéder hiperlapja, hiszen minden hiperlapja szabályos tetraéder. Hova tűnt az oktaéder? Szokás szerint a 3-dimenziós analógiát kell megvizsgálni. Pontosan úgy tűnt el az oktaéder, ahogy a négyzet eltűnik, ha oktaédert csinálunk belőle. Az oktaédernek sincs négyzet lapja. A kiindulási négyzet úgy szűnt meg lap lenni, hogy a test egyik része föléje került, a másik alája, így az oktaéder belsejében találta magát. Átjárható lett abban az értelemben, hogy például egy oktaéderbe zárt légy szabadon átrepülhet rajta.
Amikor a szabályos oktaéderből csinálunk noktaédert, a noktaéder egy része "föléje'', egy része "alája'' kerül, ezért nem határolja a noktaédert. Furcsán hangzik, de a noktaéderbe zárt 4-dimenziós légy számára az oktaéder is "átjárható''. Ezt csak azért érezzük hihetetlennek, mert ezt az "átjárást'' csak úgy tudjuk elképzelni, hogy az oktaéder egyik lapján berepül, a másikon ki. Pedig nem így tesz. Pontosan úgy tesz, ahogy 3-dimenziós kollégája tesz az oktaéderben. Ő a négyzeten úgy megy át, hogy csak egy belső pontján halad át egy pillanat alatt. A 4-dimenziós légy ugyanúgy az oktaéder egy belső pontján megy át, és csak egy pillanatot tölt a mi terünkben. Úgy érzem ez a példa is mutatja, hogy nemcsak mennyiségi, hanem minőségi különbség is van a 3- és a 4-dimenziós világ között.
A vizsgált három szabályos 4-dimenziós poliéder természetesen adódó általánosítása volt 1‐1 szabályos, 3-dimenziós testnek. A maradék 2 hagyományos szabályos testnek (a szabályos dodekaédernek és ikozaédernek) nem nagyon adódik ilyen természetes általánosítása, így joggal merülhet fel a kérdés, hogy van -e egyáltalán további szabályos 4-dimenziós test. Nos, állítólag még (így összesen ) szabályos 4-dimenziós poliéder van. Ezek megkeresése igen szép és érdekes feladat, ajánlom mindenkinek, aki ki akarja próbálni 4-dimenziós konstruktivitását. Esetleges kudarc esetén is sok érdekes dologra jön rá az ember keresés közben. Segítségül megelőlegezem a 4-dimenziós Euler-tételt, amely úgy szól, hogy "rendes'' poliéderek esetén , ahol rendre a csúcsok, élek, lapok, illetve hiperlapok száma.
Ennek az állításnak külön érdekessége van: a 3-dimenziós tér axiómái közül mindössze egynek nem felel meg a 4-dimenziós euklideszi tér. Ez az axióma így szól: két sík metszete nem lehet egy pont. |
 PDF | MathML
PDF | MathML