|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Érdekes kombinatorikus geometriai problémák
A kombinatorikus geometria egyik széles körben alkalmazott eszköze a Ramsey-tétel, amelyet többnyire egzisztenciabizonyításokban használnak fel.
A Ramsey-elmélet legegyszerűbb példája a következő ‐ bizonyára közismert ‐ feladat:
1. Feladat Bizonyítsuk be, hogy ha egy 6 tagú társaságban bármely két ember vagy barát vagy ellenség, akkor biztosan kiválasztható olyan 3 ember, akik közül vagy bármely kettő ellenség, vagy bármely kettő barát.
Ugyanez gráfelméleti kérdésként megfogalmazva:
Adott egy 6 szögpontú gráf úgy, hogy bármely két pontját pontosan egy, piros vagy kék él köti össze. Bizonyítsuk be, hogy a gráfnak van olyan 3 szögpontú teljes részgráfja, melyben minden él egyszínű. (Azaz kiválasztható 3 pont úgy, hogy bármely kettőt azonos színű él köt össze.)
Bizonyítás:
A feladatot most mint gráfelméleti kérdést kezeljük. Válasszuk ki a gráf egy tetszőleges csúcsát. Ebből összesen 5 él indul ki, mindegyik piros vagy kék, tehát van köztük legalább 3 azonos színű, mondjuk kék él. Jelölje 3 ilyen él -től különböző végpontját , és . Ha e három pont közül valamelyik kettőt kék él köti össze, akkor az a két pont -vel együtt kék háromszöget, azaz hárompontú teljes részgráfot alkot. Ha pedig az , és élek mindegyike piros, akkor piros háromszög. Ezzel a feladat állítását beláttuk.
A fenti feladat általánosítása az alábbi:
Ramsey-tétel:
Minden természetes számokból álló számpárra létezik olyan természetes szám, melyre teljesül, hogy ha egy pontú teljes gráf éleit pirosra vagy kékre színezzük, akkor van vagy pontú kék, vagy pontú piros teljes részgráfja, de ha , akkor egy -pontú teljes gráf éleit még ki lehet színezni a két színnel úgy, hogy ne teljesüljön az utóbbi állítás (azaz nincs sem pontú kék, sem pedig pontú piros teljes részgráf.)
A tétel bizonyítását nem közöljük, bár nem túl nehéz. Akik megpróbálják bizonyítani, azoknak azt javasoljuk, hogy -re és -ra vonatkozó kettős teljes indukcióval próbálkozzanak. A bizonyításból egyébként az is következik, hogy
Akkor is megfogalmazható a megfelelő állítás, ha az élek (azaz pontpárok) helyett egy halmaz pontjainak elemű részhalmazait tekintjük, és ilyenkor a megfelelő Ramsey-számot -vel jelöljük. -t egyszerűen -vel jelöljük.
Ramsey tételének igen sok érdekes következménye van, melyek közül most csak néhányat sorolunk fel.
1. Következmény: Egy kellően hosszú, különböző számból álló sorozat biztosan tartalmaz vagy egy elemű növekvő, vagy egy elemű csökkenő részsorozatot (melynek elemei nem feltétlenül szomszédosak az eredeti sorozatban, de az eredeti sorrendben vannak).
Bizonyítás:
Egyszerűen következik Ramsey tételéből, ugyanis egy hosszúságú sorozat kielégíti a feltételt. Ez a következőképpen látható be:
Számozzuk meg egy pontú teljes gráf csúcsait 1-től -ig és színezzük ki az éleket a következőképpen: ha és a sorozat -edik eleme (jelöljük -vel) kisebb -nél, akkor a gráf -edik és -edik pontját kék, ha és , akkor a gráf -edik és -edik pontját piros él kösse össze és ). Így bármely két pontot pontosan egy, piros vagy kék él köt össze, tehát Ramsey tétele szerint van vagy pontú piros vagy pontú kék teljes részgráf a gráfban, ami természetesen azt jelenti, hogy a sorozatban van vagy egy elemű csökkenő, vagy egy elemű növekvő részsorozat. Tehát, ha azt a legkisebb természetes számot jelöli, melyre egy különböző számból álló sorozatban biztos van vagy elemű csökkenő vagy elemű növekvő részsorozat, akkor értéke pontosan is meghatározható:
Bizonyítás:
 1. ábra
Először azt látjuk be, hogy . Erre egyszerű konstruktív bizonyítást adunk. Vegyünk fel darab hosszúságú növekvő sorozatot (jelöljük ezeket , , , -gyel) úgy, hogy ha , akkor legnagyobb eleme legyen kisebb legkisebb eleménél. Ilyen tulajdonságú sorozatok természetesen léteznek. A keresett sorozatot ezután úgy kapjuk, hogy az , , , , sorozatokat sorozattá fűzve rendre egymás után rakjuk. Az olvasóra bízzuk annak belátását, hogy egy ilyen sorozat nem tartalmaz sem elemű csökkenő, sem elemű növekedő részsorozatot.
(Útmutatás: A kiválasztható növekvő részsorozatok elemei csak azonos -ből származhatnak, míg egy csökkenő részsorozat két eleme nem származhat azonos -ből.)
Ezután már csak azt kell belátnunk, hogy . Ezt indirekt úton bizonyítjuk. Tegyük fel, hogy létezik olyan , , , , sorozat, amely nem tartalmaz sem tagú növekvő, sem tagú csökkenő részsorozatot. Rendeljünk a sorozat minden eleméhez egy természetes számokból álló rendezett számpárt, ahol az -vel kezdődő leghosszabb növekvő részsorozat hossza és az -vel kezdődő leghosszabb csökkenő részsorozat hossza.
Ekkor esetén nem teljesülhet egyszerre, hogy és , mert ha , akkor -t az -vel kezdődő leghosszabb növekvő részsorozat elé rakva -nél hosszabb növekvő sorozatot kapunk, tehát . Ha , akkor hasonlóan látható be, hogy .
Másrészt, ha indirekt feltevésünk igaz, akkor és , így legfeljebb darab rendezett számpárt készítettünk. Így viszont van két olyan eleme a hosszúságú sorozatnak, melyhez ugyanaz az számpár tartozik, ami ellentmond az előbb belátottaknak. Indirekt feltevésünk tehát ellentmondásra vezetett. Ezzel beláttuk, hogy .
Ramsey tétele egy igen érdekes és sokáig megoldatlan kombinatorikus-geometriai problémára is megoldást adott. A probléma egy egyszerű speciális esetét Klein Eszter 1933-ban vetette fel Erdős Pál és Szekeres György magyar matematikusoknak.
2. Feladat: Ha pont egy síkban helyezkedik el, és semelyik nem esik egy egyenesbe, akkor az pont között van pont, amelyik konvex négyszöget alkot.
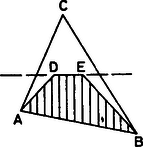 2. ábra
Bizonyítás:
Ha a ponthalmaz konvex burka - vagy -szög, akkor készen vagyunk. Ha egy háromszög a konvex burok, akkor a további pont, és a háromszög belsejében van. A egyenes nem metszi a háromszög egyik oldalát (ábránkon ez az szakasz), de ekkor az , , , pontok konvex négyszöget alkotnak.
Ezután általánosították a feladatot.
3. Feladat: Adott -ra létezik-e olyan szám, hogy minden számú általános helyzetű pont (semelyik sem esik egy egyenesre) közül mindig kiválasztható egy konvex szög?
A Ramsey-tétel és a legutóbb belátott 2. Feladat segítségével már nem nehéz megadni a kérdésre az igenlő választ. Ugyanis: | | (2) |
Bizonyítás:
"Színezzük'' a ponthalmaz minden egyes elemű részhalmazát aszerint, hogy konvex vagy konkáv, kékre, illetve pirosra. A Ramsey-tétel értelmében ekkor vagy van pont, amelyek közül bármely konvex négyszöget alkot, s így maga a pont által meghatározott sokszög is konvex, ezért készen vagyunk; vagy pedig van pont, melyek közül bármely konkáv négyszöget, alkot, de ez az elöbbi 2. Feladat miatt lehetetlen. Következésképpen most az első eset áll fönn, és így készen vagyunk.
Egy rokon probléma vizsgálatával ennél pontosabb felső becslést is adhatunk -ra.
Tekintsünk (a síkban) egy véges, általános helyzetű pontrendszert, és vegyünk föl egy olyan derékszögű koordináta-rendszert, hogy két különböző pont, megfelelő koordinátái ne egyezzenek meg. (Ezt nyilván megtehetjük, mert a pontokat csak véges számú, különböző irányú egyenes köti össze.) Nevezzük felső ívnek az alulról konkáv, alsó ívnek pedig az alulról konvex egyszerű sokszögvonalakat.
Bebizonyították, hogy pont közül már biztosan ki lehet választani vagy egy pontú alsó, vagy egy pontú felső ívet. (Ezt a bizonyítást itt nem részletezzük.)
Nyilvánvaló, hogy ha van egy pontú felső vagy alsó ívünk, akkor az ív két végpontját összekötve egy pontú konvex sokszöget nyerünk. Innen pedig adódik. Erdős Pál és Szekeres György azt sejtették, hogy , de ezt mindezidáig senkinek sem sikerült belátnia. (Az ismert, hogy -re a sejtés igaz!)
Most belátjuk, hogy a (3)-ban adott becslés éles. Ehhez megadunk egy olyan konstrukciót, hogy pont között ne legyen se pontú alsó, se pontú felső ív! Készítsünk az ábra szerint egy táblázatot!
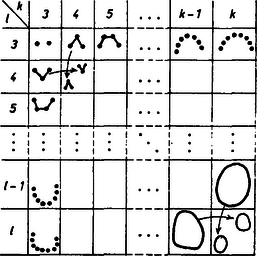 3. ábra
A táblázat -edik sorában és -adik oszlopában álló kép egy olyan ponthalmazt ábrázol, amelyben nincs sem pontú felső, sem pontú alsó ív. Most már csak azt kell belátni, hogy megadható úgy a konstrukció, hogy legyen, ahol az ábra pontjainak száma.
Az első sorban lévő, képeknek a feltétel miatt pontból kell állniuk, így lehet egy pontú felső ív. Ugyanígy a képeknek megfelelhet egy pontú alsó ív. Könnyen látható, hogy most minden kívánt feltétel teljesül.
A binomiális együtthatók ismert tulajdonsága, miatt is igaz. Tehát a egyenlőséghez ‐ az előbbi eredményeink értelmében ‐ elég lenne azt belátni, hogy a "képekre'' is hasonló teljesül, azaz előáll a és képek olyan egyesítéseként, tehát hogy . Most megadunk egy ilyen konstrukciót. (Lásd az előző ábrát). Helyezzük el a képet tetszőlegesen, és -et tőle "balra, le'' úgy, hogy az egy-egy részképen belüli pontokat összekötő bármely egyenes meredeksége legyen kisebb, mint a két halmaz 1-1 pontját összekötő bármely egyenes meredeksége. (Ezt megtehetjük, mert elhelyezhetjük úgy -et, hogy ne legyen a pontjai által meghatározott egyenesek között függőleges.) Könnyen látható, hogy ez a konstrukció jó. Ugyanis az elhelyezés miatt a -ben lévő legfeljebb pontú alsó ívhez nem csatlakozhat folytatásként semelyik pontja sem. Ugyanígy a -ben lévő legfeljebb pontú felső ívhez nem csatlakozhat semelyik pontja sem. Azt is könnyen meggondolhatja az olvasó, hogy sem a -ben tévő legfeljebb pontú alsó ívhez, sem pedig a -ben lévő legfeljebb pontú felső ívhez nem csatlakozhat a másik képből egynél több pont. Ez is a meredekségekre adott megkötés miatt igaz.
Ezzel állításunkat beláttuk, azaz a (3)-ban adott becslés valóban éles.
Feladatok
1. Próbáljuk meg belátni Ramsey tételét -re, pontosabban azt, hogy
Útmutatás: Lássuk be, hogy és azt, hogy
2. Lássuk be, hogy ha adott a síkon általános helyzetű pont, akkor legalább különböző konvex négyszöget határozunk meg. (A Moszkvai Nemzetközi Matematikai Diákolimpián egy ennél gyengébb feladat volt kitűzve, azt kellett belátni, hogy van legalább olyan konvex négyszög, melynek pontjai az adott pont közül kerülnek ki.)
3. Ugyancsak az 1964. évi moszkvai diákolimpián volt feladat a következő: 17 tudós mindegyike levelezést folytat az összes többivel. Összesen háromféle témáról leveleznek, de bármely pár mindig csak ugyanarról az egy témáról. Bizonyítsuk be, hogy van közöttük legalább 3 olyan tudós, akik közül bármely kettő azonos témáról levelezik egymással.
4. Lássuk be, hogy a 3. feladat állítása 16 tudósra még nem igaz!
5. Az 1. és 4. feladat felhasználásával lássuk be, hogy (Valójában: .)
6. Legyen , . Lássuk be, hogy ha tudós folytat levelezést összesen féle témáról, ugyanúgy, mint a 3. feladatban, akkor is van közöttük 3 olyan, akik közül bármely kettő azonos témáról levelezik.
Az Ifjúsági Matematikai Kör ülésén elhangzott előadás. Lejegyezték Futó Gábor és Horvai Péter, a budapesti Fazekas Mihály Gimnázium tanulói.A feladatokat Futó Gábor és Horvai Péter közölték |
 PDF | MathML
PDF | MathML