|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Permutációcsoportok
Definiáljuk először a permutáció fogalmát:
D.: A permutáció egy halmaz önmagára való kölcsönösen egyértelmű leképezése. A továbbiakban mi az {1, 2, .. . , n} halmaz permutációival foglalkozunk. A fenti definíció szemléletes jelentése, hogy egy permutáció az 1, 2, ... , n számok valamilyen sorrendje. Egy permutáció természetes jelölése a következő:
}.
Nyilvánvaló, hogy egy n elemű halmaz permutációinak száma ! Mindez önmagában elég semmitmondó, ezért vezessünk be egy permutációk közötti műveletet. Kézenfekvőnek tűnik a
| |
permutációk szorzatát a következőképpen definiálni: az - re alkalmazzuk -et, majd az így nyert számra -t. Könnyen látható, hogy is egy permutáció, tehát a permutációk halmaza zárt erre a műveletre nézve. A szorzás további tulajdonságai is könnyen ellenőrizhetők.
1. Asszociatív:
2. Az permutációt egységelemnek véve minden -re .
3. Minden -re létezik pontosan egy olyan , hogy . a permutáció inverze.
4. Nem kommutativ. Ezt egy példával igazoljuk:
| |
hiszen
| |
míg
| |
Tetszőleges -re pedig a következő példát készíthetjük ezek alapján
| |
Az első három tulajdonság és a zártság alapján kimondhatjuk, hogy a permutációk az itt definiált szorzásra nézve csoportot alkotnak. Ezt -nel jelöljük és -ed-fokú szimmetrikus csoportnak nevezzük.
-en belül a következő módon megkülönböztetünk páros és páratlan permutációkat: tekintsük a
szorzatot. Alkalmazzuk a permutációt minden tényezőn belül minden tagra. Így a
szorzatot kapjuk, amelynek abszolút értéke nyilván megegyezik az előbbi szorzat abszolút értékével. A permutációt párosnak mondjuk, ha a szorzat előjele megmarad, és páratlannak, ha a szorzat előjele megváltozik. Vegyük észre, hogy a permutációknak pontosan a fele páros, és a fele páratlan esetén. Tekintsük ugyanis a következő kölcsönösen egyértelmű megfeleltetést a páros és páratlan permutációk között: a páratlan permutáció segítségével rendeljük a permutációhoz a permutációt. Nyilvánvaló, hogy és közül pontosan egy páros, és egy páratlan. Paritás szempontjából vizsgálva a szorzást, a következőket állapíthatjuk meg:
Azonnal következik, hogy a páros permutációk halmaza a szorzásra nézve zárt, így az n!/2 db páros permutáció egy részcsoportját alkotja. Ennek neve -edfokú alternáló csoport, jelölése .
Térjünk vissza a permutációk jelöléséhez. Az eddigi =
jelölésnél célszerűbb az úgynevezett "ciklusos'' jelölésmód: írjuk az első helyre az 1-et, majd az (i + 1)-dik helyre rendre azt a számot, amelyet a permutáció az i-dik helyen álló számhoz rendel, kivéve, ha visszajutottunk az 1-hez; ekkor zárjuk be a ciklust, és nyissunk újat a legkisebb eddig nem szereplő elemmel. Ezt addig végezzük, amíg az összes elem sorra nem kerül. Például:
| |
(Megjegyzés: Mivel minden elemnek pontosan egy "őse'' és egy "képe'' van, egy ciklus csak az első eleméhez záródhat vissza.) Ilyen jelölésmóddal a szorzás gyorsabbá és átláthatóbbá válik.
D.: Az olyan permutációkat, amelyek ciklusos jelölésében egy kéttagú ciklus van, a többi ciklus pedig egytagú, transzpozícióknak nevezzük. Egy transzpozició tehát két elem cseréje a továbbiak helybenhagyásával.
Ha a kéttagú ciklus két szomszédos egészből áll, szomszédos transzpozícióról beszélünk.
1.T.: Minden permutáció előáll transzpozíciók szorzataként.
Bizonyítás. A permutációk ciklusos írásmódjából következik, hogy a tételt elég egyetlen ciklusra belátni. Valóban:
| |
2.T.: Minden permutáció előáll szomszédos transzpozíciók szorzataként.
Bizonyítás. Az előzőekből adódik, hogy elég a tételt transzpozíciókra belátni:
| |
3.T.: Minden permutáció előáll az (12) és az (12...) permutációkból a szorzás műveletével. Ennek bizonyítása megtalálható a KöMaL 1990/7. 303. oldalán az F.2768. feladat megoldása során.
4.T.: Egy permutáció hatványaként nem állhat elő minden permutáció.
Bizonyítás. Mivel , egy permutáció hatványai kommutatív csoportot alkotnak; márpedig nem kommutatív.
A továbbiakban szükségünk lesz egy új fogalomra.
D.: és konjugáltak egy halmazban, ha létezik olyan , melyre és
5.T.: Ha részcsoport, akkor a konjugáltság ekvivalencia-reláció:
1. reflexív:
2. szimmetrikus: ha
3. tranzitív: ha és , akkor
E tétel alapján elemei diszjunkt konjugáltosztályokba rendeződnek. (Ez egyébként minden csoportra igaz.)
Felmerül a kérdés, hogy két, ciklusszerkezetével megadott permutáció mikor konjugált -ben.
Legyen
| |
és
| |
ahol és A -nek és -nek pontosan akkor egyezik meg a ciklusszerkezete, ha és
6.T.: Két permutáció pontosan akkor konjugált -ben, ha azonos a ciklusszerkezetük.
Bizonyítás.
1.Ha és konjugáltak, azaz valamilyen -ra, akkor ciklusszerkezetük megegyezik.
Írjuk fel -et transzpozíciók szorzataként: Ekkor A szorzás asszociativitása miatt elég bizonyítani, hogy és ciklusszerkezete megegyezik. Ellenőrizhető, hogy ez a művelet nem csinál mást, mint az és a elemeket fölcseréli -ben. Így a ciklusszerkezetet nem változtatja meg.
2. Ha és ciklusszerkezete ugyanaz, akkor konjugáltak. A bizonyítás első részében használt elemfelcserélésekkel a nyilvánvalóan átvihető -be. A konjugáltság a csoportelméletben mélyebb fogalmakkal van kapcsolatban:
D.: Egy csoport olyan részcsoportját, amely minden elemének -beli konjugáltjait is tartalmazza, a normális részcsoportjának vagy normálosztójának nevezzük. Minden csoportnak van két trivális normálosztója: az egységelem és maga az egész csoport.
D.: Az olyan csoportokat, amelyeknek a két triviális normálosztón kívül nincs más normálosztójuk, egyszerű csoportoknak nevezzük.
Az egyszerű csoportok a prímszámokhoz hasonló szerepet játszanak a csoportok szerkezetében. Bizonyítható, hogy ( esetén) egyszerű csoport, és ezzel van kapcsolatban az, hogy ötöd- és ennél magasabb fokú egyenletekre nincs általános megoldóképlet. ( a legkisebb egyszerű csoport.)
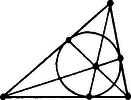 1. ábra
Érdekességként megadjuk a második legkisebb egyszerű csoportot: Vegyük a legkisebb, 7 pontból álló véges projektív síkot (1.ábra). Ezen 7 pont egyenestartó permutációi egyszerű csoportot alkotnak. (A kör is egyenesnek számít.)
Érdemes gondolkodni a következő egyszerűbb és nehezebb feladatokon:
1. Minden transzpozíció páratlan permutáció.
2. A buborékrendezés felhasználásával bizonyítsuk az 1. tételt!
3. Bizonyítsuk be a 3. tételt!
4. Mutassuk meg, hogy a kocka mozgáscsoportja izomorf -gyel!
*5. A dodekaéder mozgáscsoportja izomorf -tel!
**6. egyszerű csoport, ha
****7. konjugáltosztályainak a száma nagyobb, mint konjugáltosztályai számának a fele
A fenti előadás az Ifjúsági Matematikai Kör Téli Ankétján hangzott el. (Lejegyezték: Kőszegi Botond és Matolcsi Máté, a Budapesti Fazekas Mihály Gimn. III. osztályos tanulói.) |
 PDF | MathML
PDF | MathML