Cím: A kontinuumsejtés
Szerző(k):  Urbán János 
Füzet: 1991/január, 1 - 7. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A halmazokkal foglalkozó matematikai tudományág, a halmazelmélet alig száz éves tudomány ‐ ami a matematika igen kevés területéről mondható el. Georg Cantor (1845 ‐ 1918) német matematikus volt az, aki az 1880-as években lényegében egyedül alkotta meg a halmazelmélet alapvető fogalmait és tételeit. Kevés ilyen matematikai tudományág van, amelyről elmondhatjuk, hogy egy ember nevéhez kapcsolható!
Szinte önként adódik a kérdés, mi lehet az oka, hogy a halmazelmélet, amely nélkül a matematika szinte el sem képzelhető, ilyen későn alakult ki. Megkockáztatom azt a feltevést, hogy ennek egyik döntő oka Euklidesz (i.e. 300 körül) és művének, az ,,Elemek''-nek hatalmas tekintélye volt. Euklidesz az Elemek első könyvében az Axiómák között a 8.-ban ezt mondja: ,,Az egész nagyobb, mint a rész.'' Galilei (1564 ‐ 1642) számára ezért tűnt még paradoxonnak az a megfigyelése, hogy ugyanannyi négyzetszám van, mint ahány pozitív egész szám, hiszen a pozitív egész számok és a négyzetszámok kölcsönösen egyértelműen megfeleltethetők egymásnak:

 
 

Felcsillant a lehetősége egy olyan definíciónak, amely megállapítja, hogy két végtelen halmaz mikor tartalmaz ,,egyenlő számú'' elemet, de Euklidesz tekintélye hatott. A négyzetszámok részhalmazát alkotják a pozitív egész számok halmazának, az egész nagyobb mint a rész, tehát ez a megfigyelés csak egy paradoxon.
Bolzano (1781 ‐ 1848) cseh matematikus, halála után, 1851-ben megjelent könyve, melyben egy sor hasonló észrevétel található, még mindig ezt a címet viselte: ,,A végtelen paradoxonjai''.
Georg Cantor volt az első, aki szakítani mert a 8. axiómával és bevezette következő definíciót: két (végtelen) halmazról akkor mondjuk, hogy egyenlő a számosságuk, más szóval ekvivalensek, ha elemeik között kölcsönösen egyértelmű megfeleltetés létesíthető. Ebben az értelemben Galilei megfigyelése azt mutatja, hogy a pozitív egész számok N+ halmazának és a négyzetszámok halmazának számossága egyenlő, másképp mondva a két halmaznak ugyanannyi eleme van, a rész nem kisebb, mint az egész, a végtelen halmazok körében a 8. axióma nem igaz
Nézzünk néhány további, már Cantor gondolatmenetét felhasználó összefüggést végtelen halmazok körében.
Az egész számok Z halmaza ekvivalens a természetes számok N halmazával. Ezt például a következő kölcsönösen egyértelmű megfeleltetéssel láthatjuk be:
 
 

A megfeleltetést még rövidebben úgy is jellemezhetjük, hogy az egész számokat egy sorozatba ,,rendezzük'', és az egész számnak megfeleltetett természetes számot a sorozatban elfoglalt helye jelenti:
0,-1,1,-2,2,-3,3,...,-n,n,...

A természetes számok N halmazával ekvivalens végtelen halmazokat megszámlálhatóan végtelennek nevezzük és számosságuk jelölésére Cantor vezette be az æ0 jelölést (,, alef'' a héber ábécé első betűje).
Könnyen látható; hogy minden megszámlálhatóan végtelen halmaz sorozatba rendezhető, és megfordítva, minden olyan végtelen halmaz, amelynek elemei sorozatba rendezhetők, megszámlálhatóan végtelen.
Megmutatjuk, hogy a racionális számok Q halmaza is sorozatba rendezhető. Vegyük először az egynél kisebb pozitív racionális számok halmazát:
Q1={r∈Q∣0<r<1}
A Q1 elemeit a következő módon rendezzük sorozatba: első helyre az egyetlen, 2 nevezőjű törtet, az 12-et írjuk, azután sorra vesszük nagyság szerint a 3 nevezőjűeket, majd a 4,5,...,n... nevezőjű törtek következnek egymás közt nagyság szerint rendezve. Mivel bármely n-hez az n nevezőjű törtek közül csak véges sok van 0 és 1 között, így sorozatot kapunk, amely Q1 minden elemét legalább egyszer tartalmazza:
12,13,23,14,24,34,15,25,35,45,...
Ezután a Q2={r∈Q∣r>1} halmaz egy sorozatba rendezését úgy kaphatjuk meg, hogy az előző sorozatban minden elem reciprokát vesszük:
21,31,32,41,42,43,51,52,53,54,...
A két sorozat ,,fésűs'' egyesítésével és az 1-nek a sorozat első tagjaként való beiktatásával a pozitív racionális számok Q+ halmazának egy sorozatba rendezését kapjuk:
1,12,21,13,31,23,32,14,41,24,42,34,43,...

Világos, hogy ha most az előző sorozatban minden elemnek a -1-szeresét vesszük, akkor a negatív racionális számok Q- halmazának egy sorozatba rendezését kapjuk. Végül a Q+ és Q- halmazok elemeit tartalmazó sorozatok fésűs'' egyesítését képezve és a 0-t a sorozat első elemének véve a Q halmaz egy sorozatba rendezését kapjuk.
A racionális számok szemléletes képével ez a sorozatba rendezés kevés közös vonást mutat, hiszen jól ismert, hogy bármely két racionális szám között van racionális szám (például a két szám számtani közepe), tehát nagyság szerint nem rendezhetők sorozatba a racionális számok.
Felmerülhet itt ez a kérdés: van-e egyáltalán olyan végtelen halmaz, amelynek elemei nem rendezhetők sorozatba?
Cantor válasza: igen, a valós számok halmaza nem rendezhető sorozatba.
Mielőtt ennek bizonyítását látnánk, emlékeztetünk a valós számok legfontosabb alaptulajdonságaira. Tudjuk, hogy a valós számok körében elvégezhető a négy alapművelet (a 0-val való osztás kivételével) és teljesülnek a szokásos műveleti azonosságok. Értelmezhető a ,,kisebb'' fogalom (másképpen a rendezés) és ennek a relációnak is a megszokott tulajdonságai érvényesek. Az eddig felsorolt tényeket röviden úgy foglalhatjuk össze, hogy a valós számok rendezett (szám)testet alkotnak. Mindezek a racionális számokra is teljesülnek. A valós számok testét a racionális számok testétől megkülönböztető, karakterisztikus tulajdonság, hogy igaz rájuk a következő, ún. Cantor-tétel:
Ha adott egymásba skatulyázott zárt intervallumoknak egy sorozata, azaz minden n∈N-re egy-egy olyan [an;bn] zárt intervallum, hogy an≦an+1 és bn+1≦bn, másképpen [an+1;bn+1]⊂[an;bn] minden n-re, akkor ezek közös része nem üres, azaz
⋂n=1∞[an;bn]≠∅.
Ez a tulajdonság a racionális számokra már nem igaz.
Ezek után megmutatjuk, hogy a [0;1] intervallumbeli valós számok ,,többen vannak'', mint a természetes számok. Ez pontosan a következőt jelenti: a [0;1] intervallumnak van olyan részhalmaza, amely ekvivalens a természetes számok halmazával ‐ például az előzőkben szereplő Q halmaz, de a [0;1] intervallum nem ekvivalens a természetes számok halmazával, azaz a [0;1] intervallumbeli valós számok nem rendezhetők sorozatba.
Ezt az utóbbi állítást kell még bizonyítanunk. Tegyük fel, hogy nem igaz az állítás. Ez azt jelenti, hogy a [0;1] intervallumhoz tartozó valós számok sorozatba rendezhetők, azaz megadható egy olyan
x1,x2,x3,...,xn,...
sorozat, amelyben minden a ∈[0;1] valós szám legalább egyszer szerepel. Ebből a feltevésből ellentmondásra jutunk.
Jelölje (az egységesség kedvéért) a [0;1] intervallumot [a0;b0]. Az [a1;b1] intervallumot a következőképpen definiáljuk: ha az előző sorozatban x1>13, akkor [a1;b1] legyen a [0,13] intervallum, ha x1≦13, akkor [a1;b1] legyen a [23;1] intervallum, tehát x1∉[a1;b1]. Ezután az [a1;b1] intervallumot harmadoljuk:
 
 


és vagy az első vagy az utolsó harmadát választjuk [a2;b2]-nek úgy, hogy az x2∉[a2;b2] feltétel teljesüljön.
A megfelelő eljárást minden n∈N-re elvégezzük arra ügyelve, hogy az [an;bn] intervallum benne legyen az előzőben és xn∉[an;bn] teljesüljön.
A Cantor-tétel szerint
⋂n=0∞[an;bn]≠∅,
tehát van olyan α valós szám, amelyik eleme a közös résznek, tehát a [0;1] intervallumnak is, de α≠xn ha n∈N, azaz α kimaradt a felsorolásból. Igy ellentmondásra jutottunk, tehát az állítás igaz.
Eredményünkből nyilvánvaló, hogy az összes valós számok R halmaza sem rendezhető sorozatba. Megmutatjuk még, hogy a [0;1] intervallum ekvivalens az R halmazzal, tehát a két halmaz számossága egyenlő. Ezt a számosságot Cantor kontinuum számosságnak nevezte és a gót c-vel jelölte: C.
Először azt lássuk be, hogy a [0;1] intervallum ekvivalens a [0,1[ intervallummal. A következő módon feleltetjük meg egymásnak a két halmaz elemeit. Válasszuk ki az 1,12,13,...,1n,... részhalmazát a [0;1]-nek, ezeket sorra feleltessük meg a [0;1[-beli 12, 13, ...,1n,... elemeknek. A kimaradókat pedig önmaguknak. Ezt a megfeleltetést így írjuk le pontosan: f:[0;1]→[0;1[.
f(x)={1n+1,hax=1n,x,hax≠1n.

A megfeleltetést így szemléltethetjük: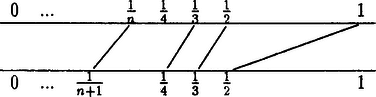
 
 

Ezek alapján nyilvánvaló, hogy a ]0;1[ nyílt intervallum is ekvivalens a [0;1[ intervallummal, tehát a [0;1] zárt intervallummal is.
Annak igazolására, hogy a ]0;1[ intervallum ekvivalens az összes valós számok R halmazával, elég meggondolni, hogy például az f(x)=1x+1x-1,x∈]0;1[ függvény kölcsönösen egyértelműen leképezi a ]0;.1[ nyílt intervallumot az R halmazra.
Azt kaptuk tehát, hogy az R halmaz számossága is C. Igazolható, hogy a természetes számok összes részhalmazának számossága is C. Ha A egy n elemű véges halmaz, akkor tudjuk, hogy A összes részhalmazainak száma 2n . Ennek analógiájára az æo számosságú N halmaz összes részhalmazainak számosságát így jelöljük: 2æo.
A végtelen számosságok bizonyos értelemben a természetes számok általánosításának tekinthetők. Bármely véges n természetes szám egy n elemű halmaz számossága, így n<æo. Megmutattuk, hogy æo<C=2æo. Már Cantor számára természetes volt a kérdés: van-e olyan végtelen számosság, amely æo és 2æo között van?
Mint ahogy minden természetes számnak van rákövetkezője (pl. 4-é 5, 100-é 101), a végtelen számosságokról is megmutatható, hogy mindegyiknek van rákövetkezője (ez természetesen nem 1-gyel nagyobb nála), az æo számosság rákövetkezőjét Cantor így jelölte: æ1. Tudjuk, hogy æ1≦2æo és Cantor kérdése így is megfogalmazható: ebben az egyenlőtlenségben a < jel vagy az = jel érvényes?
Cantor fogalmazta meg azt a sejtést, hogy a kérdésre a válasz: itt az egyenlőségjel érvényes, tehát az æo után következő számosság 2æo. Ezt hívják kontinuumsejtésnek. Maga Cantor is, és a múlt század vége óta igen sokan próbálkoztak meg a kontinuumsejtés bizonyításával. Hiszen elég nyilvánvalónak tűnik az, hogy a sejtés vagy igaz, vagy hamis. Szemléletesen úgy képzelhetjük, hogy kiindulunk például a racionális számok æo számosságú halmazából és fokozatosan elkezdjük bővíteni mindaddig, amíg el nem érjük a valós számok 2æo számosságú halmazát. Eközben egy idő után az æo számosságú halmazokból át kell lépjünk nagyobb számosságúra. Ez vagy 2æo vagy olyan számosság, ami æo és 2æo között van.
A századforduló tájára a kontinuumsejtés a matematika egyik közismert, nevezetes problémájává vált. David Hilbert (1862‐1943) német matematikus az 1900-as, Párizsban rendezett nemzetközi matematikai kongresszuson egy igen nagy hatású előadást tartott ,,Matematikai problémák'' címmel. Ebben 23 nyitott problémát sorolt fel az akkori matematika legkülönbözőbb területeiről, olyan problémákat, amelyeket a XX. századi matematikának kell majd megoldani. A 23 probléma közül az első volt a Cantor-féle kontinuumsejtés vagy kontinuumhipotézis. Hilbert igen meggyőzően érvelt a matematikai problémák megoldhatósága, a matematikus munkájának érdekes, izgalmas volta mellett: ,,egy állandó belső felhívást hallunk: íme a probléma, keresd a megoldást. A megoldást tiszta gondolkodással megtalálhatod, hiszen a matematikában nincs megismerhetetlen!''
Térjünk vissza ismét a végtelen számosságokhoz. Eddig két különböző számossággal foglalkoztunk, az æo és a 2æo számosságokkal. Önként adódik a kérdés, vannak-e további végtelen számosságok. A kérdésre már maga Cantor felelt azzal, hogy igazolta a következő tételt:
Cantor tétel: tetszőleges (végtelen) halmaz számossága kisebb, mint összes részhalmazainak számossága.
Cantor tételéből következik, hogy a természetes számok részhalmazaiból álló halmaz összes részhalmazainak halmaza 2æo-nál is nagyobb számosságú. Az így kapott halmaznak újra képezhetjük a részhalmazai halmazát, ez ismét nagyobb számosságú, mint a halmaz, és így tovább. Ezen az úton végtelen sok különböző végtelen számosságot kapunk.
Lássuk a Cantor tétel bizonyítását, amelyet újra az ,,átlós módszer'' alkalmazásával végezhetünk el.
Legyen az adott halmaz A, és A összes részhalmazainak halmaza B. Megmutatjuk, hogy A ekvivalens B egy részhalmazával. Vegyük ugyanis minden a∈A-hoz az egyedül a-t tartalmazó {a} egyelemű halmazt. A B1={{a}∣a∈A} halmaz nyilván része B-nek és ekvivalens A-val, hiszen ha minden A-beli elemhez azt a B1-beli elemet rendeljük, amelynek egyetlen eleme a, akkor ez a megfeleltetés kölcsönösen egyértelmű lesz A és B1 között.
Megmutatjuk, hogy A nem ekvivalens B-vel. Tegyük fel, hogy nem igaz az állítás, A ekvivalens B-vel, és ezt a megfeleltetést egy f függvény valósítja meg. Ha a∈A, akkor f(a)∈B, azaz f(a)⊂A. Gyűjtsük össze egy részhalmazba A-nak azokat az elemeit, amelyek nem elemei a hozzájuk rendelt halmaznak:
C={a∈A∣a∉f(a)}.
Nyilván C⊂A, tehát C∈B, de akkor van olyan c∈A, amelyre f(c)=C a feltevés szerint. Ha most c∈C=f(c), akkor C definíciója szerint c∉C. Ha pedig c∉C=f(c), akkor C definíciója szerint megint c∈C adódik. Ellentmondásra jutottunk, tehát A nem ekvivalens B-vel.
Az általánosított kontinuum probléma azt kérdezi, hogy tetszőleges a végtelen számosságra a és a nála nagyobb 2a között van-e más számosság. Az általánosított kontinuumsejtés ‐ amit szintén Cantor fogalmazott meg ‐ azt mondja ki, hogy nincs, tehát bármely a végtelen számosság és 2a között nincs más számosság.
Időközben a halmazelmélet lendületesen fejlődő és igen gyümölcsözőnek bizonyuló tudományában logikai ellentmondásokat, antinómiákat találtak. Ezeknek fő oka a halmazfogalom teljesen szabad, korlátozás nélküli alkalmazása volt. Maga Cantor így fogalmazott: halmaz ,,szemléletünk, vagy gondolkodásunk bizonyos, jól megkülönböztetett objektumainak egy egésszé való összefoglalása.'' Kiderült, hogy a halmazelmélet eredményei csak úgy menthetők meg, ha revideáljuk ezt a Cantor-féle szemléletes halmazfogalmat és szabatosan fogalmazott axiómákkal szigorúan körülhatároljuk, mely halmazok létezését fogadjuk el. Az 1930-as évek elejére kialakult a halmazelmélet ma is legáltalánosabban elfogadott axiómarendszere, a Zermelo-Fraenkel-féle axiómarendszer.
Az axiomatikus halmazelméletben azután már így merült fel a kérdés: Bizonyítható-e vagy cáfolható az axiómákból a kontinuumsejtés. 1938-ban Kurt Gödel (1906‐1978) osztrák, majd amerikai matematikusnak sikerült először egy fontos részeredményt elérnie. Megmutatta, hogy ha a halmazelmélet szokásos axiómarendszere ellentmondástalan, akkor ellentmondástalan marad akkor is, ha hozzávesszük újabb axiómaként a kontinuumsejtést. Bebizonyította tehát, hogy a szokásos axiómarendszerben a kontinuumhipotézis nem cáfolható. Nyitva maradt még az a kérdés: vajon bizonyítható-e?
Végül 1963-ban Paul J. Cohen amerikai matematikusnak sikerült megmutatni, hogy a kontinuumsejtés nem is bizonyítható a szokásos axiómarendszerben. Gödel és Cohen eredményét együttvéve úgy fogalmazhatjuk meg, hogy a kontinuum-probléma független a halmazelmélet szokásos axiómarendszerétől.
A jelenlegi helyzetet a geometriában a múlt század végén kialakult helyzethez lehet hasonlítani. Euklidesz 5. posztulátuma, a párhuzamossági axióma (ami azt mondja ki, hogy a síkban egy egyenessel egy, az egyenesre nem illeszkedő ponton át csak egy párhuzamos húzható) évszázadokon keresztül ellenállt a bizonyítási, ill. cáfolási kísérleteknek. Végül ‐ a geometria axiómarendszerének szabatos megfogalmazása után ‐ kiderült, hogy ez az axióma független a többi axiómától, sem maga, sem a tagadása nem bizonyítható a többi axiómából. Ha a párhuzamossági axiómát vesszük hozzá a többihez ‐ akkor az euklideszi geometriát kapjuk, ha a tagadását, akkor jutunk el a nemeuklideszi geometriához. Ennek mintájára azt mondhatjuk, hogy ha a szokásos halmazelméleti axiómákhoz a kontinuumsejtést csatoljuk újabb axiómaként, akkor jutunk a ,,cantori'' halmazelmélethez, ha a tagadását, akkor a ,,nemcantori'' halmazelméletet kapjuk.
Gödel, illetve Cohen bizonyítása igen mély logikai eszközöket használ, nincs mód arra, hogy részletesen ismertessük. Mindkettő a modell módszert használja, a halmazelméleten belül megkonstruál olyan objektumokat, amelyek kielégítik az axiómákat, így halmazoknak'' tekinthetők. Gödel az általa definiált objektumokat ,,konstruálható halmazoknak'' nevezte. Kiderült, hogy az így megadható halmazok elég kevesen vannak ahhoz, hogy az æ1=2æo egyenlőség teljesüljön.
Cohen bizonyítása jóval nehezebb. Neki sikerült ,,kikényszerítenie'', idegen szóval ,,forszolnia'' sok halmaz létezését úgy, hogy æ1<2æo teljesüljön.
A halmazelmélettel foglalkozó matematikusok körében ma van olyan nézet is, hogy a valós számok halmaza annyira ,,kézzelfogható'' ‐ legalábbis a matematikával foglalkozók számára ‐ , hogy minden rá vonatkozó kérdést ‐ egy jó axiómarendszerben ‐ el kell tudni dönteni. A halmazelmélet mai axiómarendszerei még át fognak alakulni, találnak majd olyan ,,természetes'' axiómákat, amelyekben a kontinuumprobléma eldönthető.