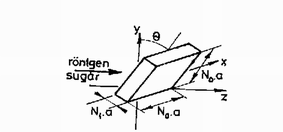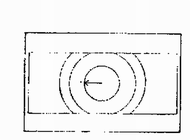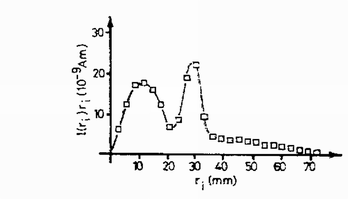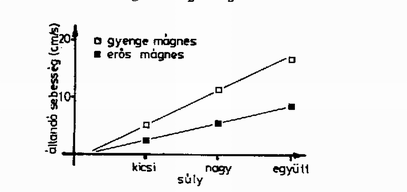Cím: 1990. A 21. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):  Gnädig Péter ,  Honyek Gyula 
Füzet: 1990/november, 401 - 412. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A versenyzőknek három elméleti feladatot kellett megoldaniuk, s ehhez öt óra idő állt rendelkezésükre.

 

1. feladat. Röntgensugarak elhajlása kristályrácson
 
Röntgensugarak elhajlását fogjuk vizsgálni egyszerű köbös kristályrácson. Először egy monokromatikus síkhullám elhajlását tanulmányozzuk. A hullám merőlegesen esik egy kétdimenziós rácsra, amely N1×N2 részből áll, ezek távolsága d1 és d2. Az elhajlási képet a rácstól L távolságra levő ernyőn észleljük. Az ernyő párhuzamos a ráccsal, továbbá L sokkal nagyobb, mint N1d1 és N2d2.
a) Határozd meg az ernyőn látható főmaximumok helyzetét és szélességét! (A szélességen a kérdéses maximumhellyel szomszédos két minimumhely közti távolságot értjük.)
Tekintsünk ezek után egy a rácsállandójú köbös kristályt, melynek mérete N0⋅a×N0⋅a×N1⋅a, ahol N1 sokkal kisebb, mint N0. A kristály az 1. ábrán látható módon kicsiny Θ szöget zár be egy z tengely menti, párhuzamos röntgensugárral. Az elhajlási képet most is a kristálytól messze elhelyezett ernyőn észleljük.
 
 

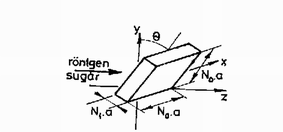1. ábra
 

b) Számítsd ki a maximumok helyzetét és szélességét a ‐ kicsinynek tekinthető ‐ Θ szög függvényében! Írd le, milyen speciális következménye van annak, hogy N1 sokkal kisebb, mint N0!
Az elhajlási kép az úgynevezett Bragg-elmélet segítségével is levezethető. Ennek lényege az a feltételezés, hogy a röntgensugarak a kristályrács atomsíkjain tükröződnek. Az elhajlási kép ezeknek a tükröződő sugaraknak egymással történő interferenciájából jön létre.
c) Mutasd meg, hogy a fenti ún. Bragg-reflexió ugyanott adja a maximumok helyét, mint azok a feltételek, melyeket a b) pontban kiszámoltál!
 
 

2. ábra
 

Bizonyos méréseknél az ún. por-módszert alkalmazzák. A röntgensugár nagyon sok, parányi kristályon szóródik. (Természetesen ezeknek a kristályoknak a mérete sokkal nagyobb, mint az a rácsállandó.) Egy kísérletben 0,15nm hullámhosszú röntgensugarakat szóratunk kálium-kloridon [KCl], amely köbös kristályrácsú (lásd a 2. ábrát). A fotolemezen koncentrikusan sötét körök jelennek meg. A kristály és a fotolemez közötti távolság 0,10m, a legkisebb kör sugara 0,053m (lásd a 3. ábrát). A K+ és a Cl- ionok lényegében ugyanakkora méretűek, így azonos szórócentrumoknak tekinthetők.
 
 

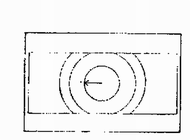3. ábra
 

d) Számítsd ki két szomszédos kálium-ion távolságát a kristályrácsban!

 
Megoldás
a) Tekintsük először az x-irányt. Ha a szomszédos résekből (ezek távolsága d1) érkező hullámok útkülönbsége:
Δ1=n1⋅λ,
ahol n1 egész szám, akkor főmaximumhoz jutunk. Ennek helye az ernyőn (x-irányban):
xn1=n1λLd1.
Ekkor a középső rés és az egyik szélső rés közötti útkülönbség:
Δ(N1/2)=N12n1λ.
Másrészről ha ez az útkülönbség:
Δ(N1/2)=N12⋅n1⋅λ+λ2,
akkor a főmaximumot követő első minimumhoz jutunk. Ennek a minimumnak az ernyőn észlelhető elhelyezkedését így adhatjuk meg:
xn1+Δx=(N12n1λ+λ2)LN12d1=n1λLd1+λLN1d1,
amiből
Δx=λLN1d1.
Ennek megfelelően a főmaximum szélessége:
2Δx=2λLN1d1.
Hasonló módon járhatunk el az y-irányban is, ahol N2 rés található egymástól d2 távolságra. A főmaximumok helyzete és szélessége tehát:
(xn1,yn2)=(n1λLd1,n2λLd2)2Δx=2λLN1d1;2Δy=2λLN2d2.


b) Az x-irányban a sugár a rácsállandójú rácsot ,,lát'', így ebben az irányban:
xn1=n1λLa;Δx=λLN0a.
Az y-irányban a sugár a⋅cosΘ effektív rácsállandójú rácsot ,,lát''. Hasonlóan az előzőekhez, így
yn2=n2λLacosΘ,Δy=λLN0acosΘ.
A z-irányban a sugár a⋅sinΘ effektív rácsállandójú rácsot ,,lát''. Ez a következő főmaximum elhelyezkedésekhez és szélességekhez vezet:
y'n3=n3λLasinΘ,Δy'=λLN1asinΘ.
Ez az elhajlási kép hozzáadódik az előzőhöz. Mivel sinΘ nagyon kicsi, csak a nulladrendű kép jelenik meg, amely azonban nagyon széles, hiszen N1sinΘ≪N0. Ha tehát egy vékony köbös kristálylapra kicsiny beesési szögben síkhullám esik, az elhajlási kép csaknem azonos lesz a kétdimenziós rács esetével.
c) Bragg-reflexiókor a szomszédos síkok interferenciát eredményező útkülönbsége:
Δ=2asinΦ≈2aΦ=nλ,
amiből
xL≈2Φ≈nλa,
tehát
x≈nλLa.
(Itt Φ az elhajlási szög.) Ez a b) alkérdéssel megegyező maximum-feltétel.
d) A szomszédos K+-ionok 2⋅a távolságát a következőképpen kaphatjuk meg:
tg(2Φ)=xL=0,0530,1=0,53,
amiből
a=λ2sinΦ≈0,15⋅10-92⋅0,24≈0,31nm,
tehát
K+-K+¯≈2⋅0,31nm≈0,44nm.

Megjegyzések: A fenti megoldásban a főmaximumok helyzetének meghatározása, a vonalszélességek számítása, valamint a Bragg-elmélet levezetése mind egyszerű meggondolásokon alapulnak, amelyeket azonban a részletesebb számítások alátámasztanak.
A pontosabb elmélet az úgynevezett szórási amplitúdó számításán alapul. (A részletes levezetés sok kézikönyvben megtalálható, lásd például Kittel: Bevezetés a szilárdtest-fizikába.) A szórt hullám intenzitása (ez észlelhető) a szórási amplitúdó abszolútérték négyzetével arányos. Például egy N rácspontból álló a rácsállandójú lineáris láncra a szórási amplitúdó négyzete a következő:
|A|2=sin2[12N(a⋅Δk)]sin2[12(a⋅Δk)]
ahol az (a⋅Δk)kifejezéskétvektorskalárszorzata.Azarácsvektorkétszomszédosrácspontotösszekötővektor,mígaΔkvektorabeesőésaszóródósugarakközöttikülönbségetjellemzi.Abeesősugaratjellemezzeazúgynevezettkhullámszámvektor,melynekirányamegegyezikabeesőnyalábbal,mígugyanígyaszóródónyalábotjellemezzükak' hullámszámvektorral. Mindkét vektor nagysága ugyanakkora:|k|=|k'|=2πλ. A Δk vektor a fenti két hullámszámvektor különbsége: Δk=k'-k. Így a szórási amplitúdóban lévő (a⋅Δk) skalárszorzat a következő módon fejthető ki:
(a⋅Δ  k)=a(k'-k)=2πλa(cosα'-cosα),
ahol α' és α a szóródó és a beeső nyaláboknak az a vektorral bezárt szögét jelentik. Az |A|2 függvény matematikai viselkedése mutatja meg a diffrakciós maximumok helyét, melynek feltétele, hogy (a⋅Δk)=2πn legyen, ahol n egész szám. Merőleges beesés esetén α=π2, tehát cosα=0, vagyis
2πn=2πλacosα',
továbbá geometriai megfontolásokból:
cosα'=nλa≈xL,
amiből
x=nλLa,
tehát megkaptuk a főmaximumok ismert helyét.
A szórási amplitúdó első minimumhelyét úgy kereshetjük meg, hogy kissé megváltoztatjuk Δk-t és definiálunk egy olyan ε számot az (aΔk)=2πn+ε kifejezéssel, hogy ε adja meg a sin[12N(aΔk)] kifejezés első nullahelyét. Könnyen megmutatható, hogy ε=2πN, tehát az elhajlási maximum szélessége arányos 1/N-nel. Ezzel visszakaptuk a hivatalos megoldás vonalszélességi eredményét. A fenti tárgyalás háromdimenziós kristályokra is érvényes, így belátható, hogy mind a köbös kristály elhajlási képe, mind a Bragg-reflexiós elmélet levezethető a szórási amplitúdó segítségével.
 

2. feladat. Elektromos kísérletek a Föld magnetoszférájában
 
1991 májusában állítják Föld körüli pályára az Atlantis űrrepülőgépet. Tegyük fel, hogy a pályája kör alakú lesz, amely a Föld egyenlítői síkjában fekszik. Egy meghatározott időpontban az űrrepülőgép kibocsát egy S szondát, s ez egy L hosszúságú elektromosan vezető rúddal kapcsolódik az Atlantishoz. Tételezzük fel, hogy a rúd merev, elhanyagolható tömegű, továbbá elektromosan szigetelő burkolat veszi körül. Mindenféle súrlódást elhanyagolunk.
 
 

4. ábra
 

Legyen α a rúd és az Atlantist a Föld középpontjával összekötő egyenes által bezárt szög (lásd a 4. ábrát)! Az S szonda szintén az Egyenlítő síkjában helyezkedik el. Tegyük fel, hogy a szonda tömege sokkal kisebb, mint az Atlantisé, továbbá L sokkal kisebb, mint a pálya sugara.
a1) Határozd meg, hogy milyen α érték(ek)nél marad a Földhöz képest változatlan az Atlantis és a szonda elhelyezkedése, vagyis milyen α érték(ek)nél marad α időben állandó?
a2) Vizsgáld meg minden esetben az egyensúly stabilitását!
Tegyük fel, hogy egy adott időpillanatban a rudat kis szöggel kitérítjük stabil egyensúlyi helyzetéből. A szonda ingaszerűen lengésbe jön.
b) Fejezd ki a szonda lengésidejét a rendszer földkörüli keringési idejének segítségével!
A 4. ábrán a Föld mágneses tere merőleges a rajz síkjára és iránya felénk mutató. A rúd pályamenti sebessége miatt a végpontjai között feszültség alakul ki. A környezet (a magnetoszféra) ritka ionizált gáz, nagyon jó elektromos vezetőképességgel. Az ionizált gázzal való elektromos érintkezést az Atlantison levő A és a szondán levő S elektródák biztosítják. A mozgás következtében I erősségű áram folyik a rúdon keresztül.
c1) Milyen irányú áram folyik a rúdban? (Legyen α=0!)
  Adatok:  ‐ a keringési időT=5,4⋅103s,  ‐ a rúd hosszaL=2,0⋅104m,  ‐ a Föld mágneses indukciójának erőssége‐a szonda környezetébenB=5,0⋅10-5Wb/m2  ‐ az Atlantis tömegem=1,0⋅105kg.
Ezek után az űrrepülőgépben levő áramforrást is bekötjük az áramkörbe, s ily módon 0,1A erősségű eredő egyenáram folyik az eddigivel ellentétes irányban.
c2) Mennyi idő szükséges ahhoz, hogy a fenti áram hatására a pályasugár fokozatosan 10m-rel megváltozzék? (Tegyük fel, hogy α mindvégig nulla marad! Hanyagoljuk el a magnetoszférában folyó áramok valamennyi hatását!) Csökken vagy pedig növekszik a pályasugár?
 
Megoldás. Az mF tömegű Föld körül R sugarú körpályán egyenletes Ω szögsebességgel keringő űrrepülőgép mozgásegyenlete:
mRΩ2=f⋅m⋅mFR2,
ahonnan
Ω2=f⋅mFR3.

 
 

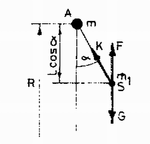5. ábra
 

Vizsgáljuk meg a szondára ható erőket az Atlantis űrrepülőgéppel együttmozgó, forgó koordinátarendszerből nézve. Az 5. ábrán látható helyzetben a gravitációs erő nagysága
G=f⋅m1⋅mF(R-L⋅cosα)2,
a ,,centrifugális erő''
F=m1⋅(R-Lcosα)⋅Ω2,
ezeken kívül fellép még valamekkora K nagyságú ,,rúderő'', valamint mozgó szonda esetében a Coriolis-erő; ez utóbbi a további vizsgálódás során nem játszik szerepet. Tekintettel arra, hogy a rúd hossza sokkal kisebb, mint a Föld sugara, G és F irányának változásától eltekinthetünk.
A szonda egyensúlyának feltétele az, hogy G és F eredőjének ne legyen K-ra merőleges komponense:
(G-F)sinα=0.

A fenti egyenletnek α1=0 és α2=180∘ nyilván megoldása, a zárójelben álló mennyiség pedig α3=90∘-nál és α4=270∘-nál válik nullává.
A szondának tehát négy egyensúlyi helyzete van. Könnyen belátható, hogy ezek közül az ,,alsó'' és a ,,felső'' helyzet stabil, míg a két ,,oldalsó'' helyzet instabil egyensúlynak felel meg. Ha például az α3 helyzetből egy kicsit kitérítjük a szondát lefelé, akkor a gravitációs erő nőni, a centrifugális erő pedig csökkenni kezd, tehát G-F lefelé mutat, s így egyre jobban el akarja távolítani a szondát az egyensúlyi helyzetétől. Ugyanez érvényes az α4-nek megfelelő helyzetre is. Mivel az alsó oldalon csak az α1=0, a felső oldalon pedig az α2=180∘-os helyzetekben valósul meg az erőegyensúly, ezek nyilván stabilak kell legyenek.
Az alsó egyensúlyi helyzet közelében (tehát cosα≈1 esetén) G és F eredőjének nagysága:
G-F=f⋅m1⋅mF(R-Lcosα)2-m1⋅(R-Lcosα)⋅Ω2≈≈f⋅m1⋅mF⋅[1(R-L)2-R-LR3]=f⋅m1mFR2[(1-LR)-2-(1-LR)]≈≈3f⋅m1mF⋅LR3=3m1⋅L⋅Ω2.


(Az utolsó előtti lépésnél kihasználtuk, hogy L≪R.) Látható, hogy a szondára a rúderőn kívül egy a tömegével arányos nagyságú, függőleges irányú erő hat, éppen olyan, amilyen egy g*=3LΩ2 gravitációs gyorsulású homogén nehézségi erőtérben hatna. Ez utóbbiban viszont egy L hosszúságú matematikai inga lengésideje:
T=2πLg*=2π13(T02π)2=T03,
ahol T0 az Atlantis keringési ideje.
A Föld mágneses tere a mozgó vezetőben feszültséget indukál, s ennek hatására a rúdban a szondától az űrrepülőgép felé áram folyik. Ha az áramerősséget ,,erőszakkal'' ellentétesirányú, I nagyságúra változtatjuk, akkor a mágneses mező
FB=I⋅B⋅L=0,1N
nagyságú erővel ,,gyorsítja'' a rendszert. Az idézőjel arra figyelmeztet, hogy a gyorsítás sebesség nagyságának nem a növekedését, hanem éppen ellenkezőleg, a csökkenését eredményezi (asztronautikai paradoxon).
A körpályán, vagy ahhoz közeli pályán keringő űrrepülőgép összenergiája:
E=12mv2-f⋅m⋅mFR=-12⋅f⋅m⋅mFR.
Ez az energia Δt ideig ható F nagyságú erő következtében ΔE=F⋅v⋅Δt értékkel változik meg, feltéve, hogy F és v azonos irányú vektorok; esetünkben ez teljesül. Másrészt
2⋅ΔE=-f⋅m⋅mF(1R+ΔR-1R)≈f⋅m⋅mF⋅ΔRR2,
ahol ΔR a pálya sugarának megváltozása. A fenti összefüggések és a mozgásegyenlet felhasználásával végül az űrrepülőgép megemeléséhez szükséges időre
Δt=m⋅ΔRFB⋅T⋅π≈5,8⋅103s  adódik.

3. feladat. Forgó neutroncsillag
 
A ,,milliszekundomos pulzár'' olyan kozmikus sugárforrás, amely nagyon rövid impulzusokat bocsát ki néhány ms-os periódusidővel. Ez a sugárzás a rádióhullámok tartományába esik; megfelelő vevőkészülékkel az egyes impulzusokat külön-külön észlelhetjük, s ily módon a periódusidőt nagy pontossággal meghatározhatjuk.
Ezek a rádióimpulzusok egy különleges csillag, az ún. neutroncsillag felszínéről származnak. Ezek a csillagok nagyon tömörek: tömegük a Nap tömegének nagyságrendjébe esik, sugaruk azonban csak néhányszor tíz kilométer. Nagyon gyorsan forognak. A gyors forgás következtében a neutroncsillag kismértékben belapul. Tegyük fel, hogy a felületének a forgástengelyre illeszkedő síkmetszete olyan ellipszis, melynek tengelyei csaknem egyenlő hosszúságúak.
Legyen rp a pólus felé mutató sugár, re pedig az egyenlítői sugár, és definiáljuk a ,,lapultságot'' a következő módon:
ε=(re-rp)/rp.
  Legyen a neutroncsillag  tömege2,0⋅1030kg,átlagos sugara1,0⋅104m,forgási periódusideje2,0⋅10-2s.

a) Számítsd ki a neutroncsillag lapultságát!
(A gravitációs állandó 6,67⋅10-11N⋅m2⋅kg-2.)
Hosszú idő (néhány év) alatt az energiaveszteség következtében a csillag forgása lelassul, s ez a lapultság csökkenésével jár együtt. A csillag felszínén azonban szilárd kéreg található, s ez a csillag folyékony belső részén úszik. A szilárd kéreg megakadályozza az egyensúlyi alak folytonos kialakulását. Ehelyett ,,csillagrengések'' játszódnak le, amelyek gyors változásokat okozva módosítják a kéreg alakját az egyensúlyi forma irányába. Ilyen csillagrengések alatt és után a megfigyelhető szögsebesség a 6. ábrán látható módon változik.
 
 

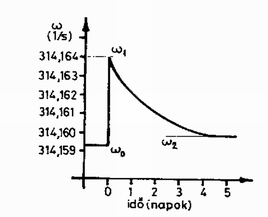6. ábra
 

b) Az ábra adatai alapján számítsd ki a folyékony belső rész sugarát! Tekintsd a köpeny és a belső rész sűrűségét azonosnak! (Hanyagold el a belső rész alakváltozását!)
 
 

7. ábra
 

Megoldás. A 7. ábrán egy forgó neutroncsillag ellipszis alakú keresztmetszete látható, szándékosan eltorzított arányokkal. Az ellipszis egyenlete
x2re2+y2rp2=1.
Írjuk fel ezt az egyenletet az (x,y) és a hozzá közeli (x+Δx, y+Δy) oordinátájú pontra, majd vonjuk ki a két egyenletet egymásból. A kicsiny Δx és Δy mennyiségek négyzetét elhanyagolva az
x⋅Δxre2+y⋅Δyrp2=0
összefüggést kapjuk.
A csillag felszínén levő m tömegű anyagdarabkára a G gravitációs erő, valamint a közvetlen közelében levő anyag által kifejtett N ,,nyomóerő'' hat. Mivel a csillag csak egy nagyon kicsit lapult, feltételezhetjük, hogy G a csillag középpontja felé mutat és a nagysága a felszín minden pontjában jó közelítéssel ugyanakkora: G=f⋅m⋅M/r2, ahol M a csillag tömege, r pedig az átlagos sugara.
Az N vektor iránya könnyen deformálódó (például folyékony halmazállapotú) testeknél merőleges kell legyen a felszínre (pontosabban fogalmazva a felület érintősíkjára), vagyis a 7. ábra jelöléseivel
NxNy=-ΔyΔx=rp2re2⋅xy.

A G és az N erő hatására a vizsgált anyagdarabka a=m⋅x⋅ω2 centripetális gyorsulású körmozgást végez az y-tengely körül. A mozgásegyenlet megfelelő komponensei:
-G⋅xr+Nx=-m⋅x⋅ω2,-G⋅yr+Ny=0.



A fenti egyenletekből az Nx/Ny arányt kifejezve, s azt a korábbi számolás eredményével összevetve
Grx-m⋅ω2⋅xGr⋅y=(rpre)2⋅xy
adódik. Ez az összefüggés a felület minden pontjában teljesül, ha fennáll, hogy
(rpre)2=1-m⋅r⋅ω2G=1-r3ω2f⋅M≈(1-r3⋅ω22⋅f⋅M)2
ahonnan
ε=1-rpre=r3⋅ω22⋅f⋅M≈3,7⋅10-4.

A csillagrengés következtében a kéreg Θk tehetetlenségi nyomatéka hirtelen lecsökken valamekkora ΔΘk értékkel. Nagyon rövid idő alatt a folyékony belső rész nem képes számottevő perdületet átadni a kéregnek, így a kéreg szögsebességének (a perdületmegmaradás törvénye értelmében) meg kell változnia:
Θk⋅ω0=(Θk-ΔΘk)⋅ω1,
ahonnan
ΔΘk=Θk⋅ω1-ω0ω1.
Elegendő hosszú idő után a folyékony belső rész és a kéreg szögsebessége kiegyenlítődik. Mivel a csillag egésze zárt rendszernek tekinthető, a perdületmegmaradás törvénye most is alkalmazható. A folyékony belső rész tehetetlenségi nyomatékát Θf-fel jelölve
(Θf+Θk)ω0=(Θf+Θk-ΔΘk)ω2,
s innen
ΔΘk=(Θf+Θk)ω2-ω0ω2.
A ΔΘk-ra kapott kétféle kifejezés összevetéséből, valamint az állandó sűrűség esetén fennálló Θ∼M⋅r2∼r5 arányosságból végül azt kapjuk, hogy
rfr=ΘfΘk+Θf5=1-(ω2-ω0)ω1(ω1-ω0)ω25≈0,98.


Kísérleti forduló
 
A versenyzőknek két kísérleti feladatot kellett megoldaniuk, kétszer 2,5 óra alatt. A továbbiakban vázlatosan ismertetjük ezek lényegét, illetve lehetséges megoldásukat.
4. feladat. Egy LED hatásfokának meghatározása
Ebben a kísérletben a diákok két modern félvezető eszközzel, fénykibocsátó diódával (LED), illetve fotodiódával dolgoztak. Három mérési feladatot kaptak:
a) kalibrálniuk kellett a fotodiódát,
b) meg kellett határozniuk, mekkora áram esetén maximális a LED hatásfoka.
c) meg kellett adniuk a LED maximális hatásfokának számértékét.

A feladat megoldásához elméleti és gyakorlati útmutatást kaptak. A rövid elméleti leírás a következő volt:
Egy LED-ben az elektromos energia egy része elektronok gerjesztését szolgálja, melyek így magasabb energiaszintekre kerülnek. Amikor egy ilyen gerjesztett elektron alacsonyabb energiaszintre kerül vissza, Efoton energiájú fotont bocsát ki, ahol
Efoton=h⋅c/λ.
Itt h a Planck-állandó, c a fénysebesség, λ a kibocsátott fény hullámhossza.
A LED hatásfokát a Φ kisugárzott teljesítmény és a felhasznált PLED elektromos teljesítmény aránya határozza meg a következő módon:
η=Φ/PLED.

A fotodiódában a sugárzási energia elektromos energiává alakul át. Ha fény jut a fotodióda érzékelő felületére, néhány (de nem az összes) foton kiszabadít valahány elektront a kristály anyagából (de nem mindegyiket). A másodpercenként érkező fotonok Nf számának és a másodpercenként kilépő elektronok Ne számának arányát kvantum-hatásfoknak (qf) nevezzük:
qf=Ne/Nf.
A gyakorlati útmutatásban megadták a fotodióda kvantum-hatásfokát (qf=0,88), a fotodióda érzékelőfelületét (2,75×2,75mm2), a LED által kibocsátott fény hullámhosszát (λ=635nm), illetve a szükséges fizikai állandók értékét. Közölték annak az áramköri panelnek a kapcsolási rajzát, amely biztosította a LED és a fotodióda (PD) működését (8. ábra). Megadták az R1 és R3 ellenállás értékét, így a diákok a rendelkezésükre álló multiméter segítségével, melyet csak feszültségmérő üzemmódban használhattak, meghatározhatták a LED-re és a fotodiódára eső feszültséget, illetve a rajtuk átfolyó áramot. A fotodiódát és a LED-et tartalmazó két dobozt szabadon mozgathatták egy milliméterpapírral borított lapon. Megtudhatták végül még azt is, hogy a fotodióda kalibrálásakor feladatuk az, hogy kísérletileg igazolják a fotodiódán átfolyó áram, illetve a ráeső fényintenzitás közötti kapcsolat linearitását.
 
 

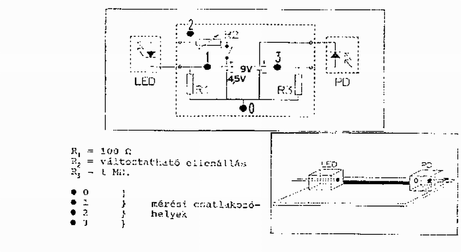8. ábra
 

A megoldás az intenzitás és a távolság közötti ismert összefüggés (I∼1/x2) használatán alapszik, ugyanis állandó LED teljesítmény mellett meg kell mérni a fotodiódán folyó áramot, majd ábrázolni az 1I értéket x függvényében. A versenyzőknek észre kellett (volna) venniük, hogy a helyes áramértékhez a háttérvilágításból származó fényt is számításba kell venni. A kapott egyenes igazolja a kérdéses linearitást. Az egyenes nem megy át az origón, a mérések szerint az x-tengelyt körülbelül a -3cm-nél metszi, ami megmutatja, hogy a fotodióda érzékelő felülete a dobozon lévő nyílás mögött hozzávetőlegesen 3cm-re helyezkedett el.
A LED hatásfoka az eddigiek alapján arányos a fotodiódán átfolyó (háttérrel korrigált) I áram és a LED-re eső teljesítmény hányadosával (η∼I/PLED). A megfelelő áram- és feszültség értékek meghatározásakor figyelembe kellett (volna) venni a multiméter megadott belső ellenállását is. Az I/PLED-ILED grafikon alapján megállapítható volt, hogy a maximális hatásfok ILED=6mA áramhoz tartozott, kisebb áramok esetén a hatásfok rohamosan, míg nagyobb áramoknál csak kis mértékben, fokozatosan csökkent.
A LED maximális hatásfokának számszerű meghatározásához vizsgálni kellett a kibocsátott hengerszimmetrikus fénykúp intenzitásviszonyait. A fotodióda d2 érzékelő felületével megadhatjuk a szimmetriatengelytől ri távolságra az ottani Φ(ri) fényintenzitást az I(rt) fotodióda áram segítségével, majd összegezhetjük a kapott gyűrűk intenzitásait a teljes Φ kisugárzott teljesítmény meghatározása céljából a következő módon:
I(ri)=Nee=Nf⋅qf⋅e=Φ(ri)h⋅ν⋅qf⋅e,Φ=∑iΦ(ri)2πridd2=2πd∑iΦ(ri)ri=2πdh⋅νqfe∑iI(ri)ri


A fénykúp intenzitásviszonyait jellemző I(ri)⋅ri függvény grafikonját a 9. ábrán láthatjuk. Az összegzés elvégzése után a LED hatásfoka az η=Φ/PLED definíció alapján körülbelül egy ezreléknek adódott.
 
 

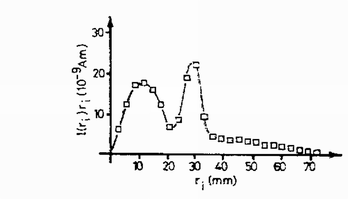9. ábra
 

5. feladat. Két különböző mágnes mágneses térerősségarányának meghatározása
 
A versenyzőknek egy tűcsapágyakkal ellátott alumínium korong mozgását kellett vizsgálniuk. A korong mozgását a tartószerkezethez rögzíthető két mágnespár valamelyike fékezte a fellépő örvényáramok következtében (10. ábra). Az erről szóló rövid elméleti bevezető így hangzott:
Ha egy vezető mágneses mezőben mozog, benne áramok indukálódnak, ezek az ún. örvényáramok. A mágneses mező és az indukált áramok kölcsönhatása következtében a mozgó vezetőre fékező erő hat. Így egy alumínium korong, amely egy állandó mágnes közelében mozog, fékező erőt érez.
 
 

10. ábra
 

A korong mozgását a tengelyére csévélt fonálon csüngő súly biztosította. A diákoknak két súly állt rendelkezésükre, melyek tömegaránya 1:2 volt. Sokan nem vették észre, hogy ez háromféle mérést tesz lehetővé, hiszen a két súly együttesen is használható. A súly elengedése után (amint ez a gyakorlati útmutatásban szerepel) a korong egyre gyorsabb forgásba jön, majd szögsebessége egy állandó értéket vesz fel. A végsebesség ‐ többek között ‐ a mágnespárok B1 és B2 térerősségétől függ. A versenyzőknek a következő mérési feladatokat kellett elvégezniük:
‐ Tervezz olyan mérést, amelyben a mágnespárok B1 és B2 térerősségeinek aránya minél pontosabban meghatározható!
‐ Add meg ‐ röviden ‐ annak elméleti levezetését, hogyan kapható meg a mérési adatokból a keresett arány!
‐ Végezd el a mérést és határozd meg az arányt!
‐ Végezz hibaszámítást!
A megoldáshoz a következő elméleti meggondolásra volt szükség: A korong egyenletes mozgásakor a fonálon lévő súlyra ható nehézségi erőből származó forgatónyomaték (mgr) egyensúlyt tart az örvényáramokból adódó MB, illetve a súrlódásból származó MS fékező nyomatékok összegével:
mgr=MB+MS.


Jogos és szokásos feltenni, hogy MS állandó, de nem elhanyagolható. (A magyar versenyzők többsége sajnos a súrlódást nem vette figyelembe.) Könnyű meggondolni, hogy az örvényáramok nagysága B-vel és a szögsebességgel arányos, így a Lorentz-erő B négyzetével és a szögsebességgel arányos, vagyis egy C állandó segítségével a mágneses fékező nyomaték MB=CB2ω alakban adható meg. A fentiek alapján, ω=ve/r figyelembevételével, az egyenletesen mozgó súly ve sebessége:
ve=gr2CB2(m-MSgr),
vagyis az állandó sebesség m lineáris függvénye.
Kísérletileg először is megfelelő időmérésekkel igazolni kellett, hogy a korong mozgása egyenletes, illetve meghatározott út után a súlyok már állandó sebességgel mozognak. Meg kellett határozni ezeket a sebességeket a háromféle lehetséges terhelésnél, mindkét mágnes esetén. A végsebesség‐súly grafikonok a 11. ábrán láthatók. A vízszintes tengelymetszetből az MS súrlódási fékező nyomatékra következtethetünk, míg a két egyenes meredeksége négyzetgyökének az aránya közvetlenül megadja a mágneses térerősségek arányát. Megfelelő hibaszámítás után a végeredmény: B1/B2=0,69±0,03.
 
 

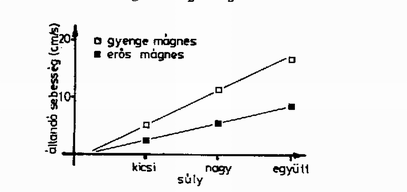11. ábra