Cím:	1989-90. Beszámoló a fizika OKTV feladatairól
Szerző(k):	Honyek Gyula
Füzet:	1990/október, 321 - 326. oldal	PDF  |  MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Első forduló   1. feladat. Egy zárt tartályban összesen $2\mathrm{,}2\text{<span style="font-style: italic;"> kg</span>}$ tömegű, héliumból és oxigénből álló gázkeverék van $0{}^{\circ }\text{<span style="font-style: italic;">C</span>}$ hőmérsékleten. A gázkeverékkel $143500$ joule hőt közöltünk és hőmérséklete $50{}^{\circ }\text{<span style="font-style: italic;">C</span>}$-kal, nyomása $13740\text{<span style="font-style: italic;"> pascallal</span>}$ növekedett.   a) Mennyi mindegyik gáz tömege? b) Mekkora volt a gázkeverék eredeti nyomása? c) Mekkora az edény térfogata?   A hélium molhője állandó térfogaton 12 300 J/($\text{kmol}\cdot \text{K}$), az oxigén molhője állandó térfogaton 20 500 J/($\text{kmol}\cdot \text{K}$).   Megoldás. $a)$ A héliumból $x$, az oxigénből $y$ kmol van jelen. Az egyenletek: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 4x+32y}& {\displaystyle =2\mathrm{,}\mathrm{2,}}\hfill \\ \hfill {\displaystyle \left(12300x+20500y\right)\cdot 50}& {\displaystyle =143500.}\hfill \end{array}}$ Az egyenletrendszer megoldása: ${\displaystyle \begin{array}{c}\hfill {\displaystyle x=0\mathrm{,}15\text{ kmol};\left(0\mathrm{,}6\text{ kg}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle y=0\mathrm{,}05\text{ kmol};\left(1\mathrm{,}6\text{ kg}\right)\mathrm{.}}\hfill \end{array}}$ $b)$ Gay-Lussac második törvénye szerint: $\begin{array}{c}{\displaystyle \frac{p}{273}=\frac{p+13740}{323}\mathrm{,}\text{innen}p=0\mathrm{,}75\cdot {10}^5\text{ Pa}\mathrm{.}}\end{array}$ $c)$ Összesen $0\mathrm{,}15+0\mathrm{,}05=0\mathrm{,}2$ kmol gázunk van, ennek normáltérfogata $0\mathrm{,}2\cdot 22\mathrm{,}4=4\mathrm{,}48{\text{ m}}^3$. Boyle‐Mariotte törvénye szerint: $\begin{array}{c}{\displaystyle 1\mathrm{,}013\cdot {10}^5\cdot 4\mathrm{,}48=0\mathrm{,}75\cdot {10}^5\cdot V\mathrm{,}\text{innen}V=6\mathrm{,}05{\text{ m}}^3\mathrm{.}}\end{array}$   2. feladat. Egy $r=0\mathrm{,}5\text{<span style="font-style: italic;"> méter</span>}$ sugarú félhenger vízszintes helyzetben rögzítve van (1. ábra). Széléhez $L$ hosszúságú fonál van erősítve. 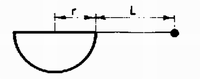    1. ábra   Vízszintes helyzetből elengedjük a fonál végén levő testet. Amikor a fonál végén levő test fölfelé halad, akkor egy bizonyos helyzetben a fonál lazává válik. Ebben a pillanatban a fonál szabad részének hossza $s=0\mathrm{,}96r=0\mathrm{,}48\text{<span style="font-style: italic;"> méter</span>}$. Mennyi a fonál teljes hossza?   Megoldás. A meglazulás pillanatáig a fonál szabad része a félhenger érintőjeként helyezkedik el a mozgás során. Könnyű belátni, hogy a meglazulás pillanatában az érintési ponttól a test felé a fonál a 2. ábrán látható módon emelkedik. Az $m$ tömeg helyzetét az $\alpha$ szöggel jellemezhetjük, így a test $y$ mélysége a következő módon fejezhető ki: 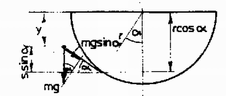$\begin{array}{c}{\displaystyle y=r\cdot \text{cos}\alpha -s\cdot \text{sin}\alpha \mathrm{.}}\end{array}$ A test sebessége az energiatétel alapján: $\begin{array}{c}{\displaystyle v^2=2gy=2g\left(r\cdot \text{cos}\alpha -s\cdot \text{sin}\alpha \right)\mathrm{.}}\end{array}$     2. ábra   A meglazulás pillanatában a kötélerő nulla, ezért az $s$ sugarú körpályán tartáshoz szükséges centripetális erőt egyedül a nehézségi erő fonálmenti komponense szolgáltatja: $\begin{array}{c}{\displaystyle mg\cdot \text{sin}\alpha =m\frac{v^2}{s}\mathrm{.}}\end{array}$ A sebességre kapott eredmény felhasználásával: $\begin{array}{c}{\displaystyle s\cdot \text{sin}\alpha =2\cdot \left(r\cdot \text{cos}\alpha -s\cdot \text{sin}\alpha \right)\mathrm{,}}\end{array}$ amiből: $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{2r}{3s}=\frac{2r}{3\cdot 0\mathrm{,}96r}=0\mathrm{,}\mathrm{694,}\text{mivel}s=0\mathrm{,}96r\mathrm{.}}\end{array}$ Ebből a keresett szög: $\begin{array}{c}{\displaystyle \alpha =34\mathrm{,}{8}^{\circ }=0\mathrm{,}607\text{ radián}\mathrm{.}}\end{array}$ A fonál teljes hossza: $\begin{array}{c}{\displaystyle L=s+\left(\alpha +\frac{\pi }{2}\right)r=3\mathrm{,}14r=1\mathrm{,}57\text{ m}\mathrm{,}}\end{array}$ vagyis a fonál teljes hossza megegyezik a félkör kerületével.   3. feladat. Egy $5{\text{<span style="font-style: italic;"> cm</span>}}^2$ és egy $10{\text{<span style="font-style: italic;"> cm</span>}}^2$ alapterületű hengert vékony cső köt össze, amelyet csappal lehet elzárni. A hengerek az asztalon fekszenek. Mindegyik hengerben $20\text{<span style="font-style: italic;"> cm</span>}$ hosszúságban $10{\text{<span style="font-style: italic;"> N/cm</span>}}^2$ nyomású levegő van. A külső légköri levegő nyomása is $10{\text{<span style="font-style: italic;"> N/cm</span>}}^2$. A bal oldali dugattyút fonál köti a falhoz (3. ábra). A hőmérséklet állandó marad. 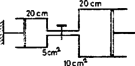    3. ábra   a) Elzárt csap mellett a jobb oldali dugattyút addig húzzuk ki, amíg a jobb oldali hengerben a légoszlop hossza $25\text{<span style="font-style: italic;"> cm</span>}$ lesz. Milyen most a bal oldali hengerben a légoszlop hossza? b) Ezután kinyitjuk a csapot és elengedjük a jobb oldali dugattyú fonalát. Milyen hosszú ezután a bal oldali hengerben a légoszlop hossza?   Megoldás. $a)$ Ha a jobb oldali hengerben a légoszlop hossza 25 cm/20 cm=5/4-szeresére nő, akkor benne a nyomás 4/5-részére csökken, vagyis $4/5\cdot 10=8{\text{ N/cm}}^2$ értékű lesz. Így a külső és a belső nyomás különbsége $2{\text{ N/cm}}^2$, tehát a jobb oldali dugattyú fonalát $2{\text{ N/cm}}^2\cdot 10{\text{ cm}}^2=20\text{ N}$ erővel kell tartanunk. Az egész rendszer akkor van egyensúlyban, ha a bal oldali dugattyú fonalában is 20 N erő lép fel. Ennek oka az, hogy a külső és belső nyomások különbségéből származó erők a dugattyún, illetve a dugattyúval szemben levő falon megegyeznek, tehát a két henger ‐ mint egyetlen merev test ‐ így van egyensúlyban. A bal oldali hengerben a nyomáskülönbség (20 N)/(5${\text{ cm}}^2$)=4 N/${\text{cm}}^2$, vagyis ott a nyomás 10-4=6 N/ ${\text{cm}}^2$ értékű, tehát a légoszlop hossza a bal oldalon: $\begin{array}{c}{\displaystyle 20\cdot \frac{10}{6}=33\mathrm{,}33\text{ cm}\mathrm{.}}\end{array}$ $b)$ Ha a jobb oldali dugattyú fonalát elengedjük, akkor az előzőek alapján a külső és a belső nyomások meg fognak egyezni, vagyis az eredeti 100+200=300 ${\text{cm}}^3$-es össztérfogat visszaáll. A feladat megoldása határozatlan, hiszen csak azt köti ki, hogy a két hengerben az össztérfogat 300 ${\text{cm}}^3$ legyen, az egyes hengerekben ezen belül a térfogat tetszőlegesen változhat a csap kinyitása és a fonál elengedésének körülményeitől függően. Ha először a fonalat engedjük el, és csak később nyitjuk ki a csapot, akkor természetesen a kezdeti állapotba jutunk vissza (ekkor a csap kinyitásának nincs szerepe). Ha először a csapot nyitjuk ki, miközben a dugattyúkat rögzített helyzetben tartjuk, akkor a kettős henger jobbra elmozdul, hiszen a levegő a nagyobb nyomású helyről átáramlik az alacsonyabb nyomású hengerbe. A folyamat a közös nyomás eléréséig tart. A két oldalon a fonalakban meg kell egyeznie az erőknek, ami a nyomáskülönbség és a felület szorzataként adható meg. Mivel a két hengerben a felület eltérő, a szorzat csak akkor egyezhet meg, ha a nyomáskülönbség nulla, vagyis a rendszerben visszaáll a $10{\text{ N/cm}}^2$-es nyomás. Könnyű belátni, hogy ekkor a jobb oldali hengerben a légoszlop $1\mathrm{,}67$ cm hosszú, míg a bal oldalon $56\mathrm{,}67$ cm hosszú lesz, hiszen így az össztérfogat: $1\mathrm{,}67\cdot 10+56\mathrm{,}67\cdot 5=300{\text{ cm}}^3$, továbbá a két légoszlop teljes hossza $1\mathrm{,}67+56\mathrm{,}67=33\mathrm{,}33+25=58\mathrm{,}33$ cm változatlan marad. Ekkor viszont a fonál elengedése lesz hatástalan a továbbiakra. Ha viszont egyszerre engedjük el a fonalat és nyitjuk ki a csapot, akkor a végállapotot a henger és a dugattyú, illetve a henger és az asztal közötti súrlódási viszonyok határozzák meg, amit eddig a feladatban hallgatólagosan elhanyagolhatónak tekintettünk. Így a végállapot a feladat szerint valóban határozatlan.   4. Feladat. Egy $R=0\mathrm{,}2\text{<span style="font-style: italic;"> méter</span>}$ sugarú tömör hengert tengelyének végpontjaiban tű-csapágyak tartanak. A henger palástján levő csavarvonalú pályán súrlódásmentesen lecsúszik egy test, amelynek tömege a henger tömegének ötöde $\left(4.\text{<span style="font-style: italic;"> ábra</span>}\right)$. A csavarvonal menetmagassága 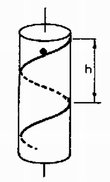$h=0\mathrm{,}2\text{<span style="font-style: italic;"> méter</span>}$. $g=10\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mspace width="0.5ex"></mspace><mi>m</mi><mo stretchy="false">/</mo><mi>s</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$.     4. ábra   a) Mekkora lesz a test sebessége az indulástól számítva $h=0\mathrm{,}2\text{<span style="font-style: italic;"> méteres</span>}$ szintkülönbség megtétele után? b) Mennyi idő alatt éri el a test ezt a sebességet?   Megoldás. A lecsúszó test földhöz viszonyított sebességének vízszintes összetevője $v_1$, függőleges összetevője $v_2$. A lecsúszó test tömege $m$, a henger tömege $5m$, a henger tehetetlenségi nyomatéka $\Theta =2\mathrm{,}5m{R}^2=0\mathrm{,}1m$; a henger szögsebessége $\omega$. a) Az energiamegmaradás tétele szerint: $\begin{array}{c}{\displaystyle 0\mathrm{,}5m\left(v_1^2+v_2^2\right)+0\mathrm{,}5{\omega }^2\Theta =mgh\mathrm{.}}\end{array}$ Az impulzusnyomaték megmaradása következtében: $\begin{array}{c}{\displaystyle m{v}_{1}R=\omega \Theta \mathrm{.}}\end{array}$ A $h/\left(2\pi R\right)$ meredekségű lejtőn a kényszerfeltétel meghatározásakor a henger kerületi sebességét is figyelembe kell venni: $\begin{array}{c}{\displaystyle \frac{v_2}{v_1+R\omega }=\frac{h}{2\pi R}\mathrm{.}}\end{array}$ A számadatok behelyettesítése után: $\begin{array}{c}{\displaystyle v_1^2+v_2^2+0\mathrm{,}1{\omega }^2=4;v_1=0\mathrm{,}5\omega ;v_2=0\mathrm{,}16\left(v_1+0\mathrm{,}2\omega \right)\mathrm{.}}\end{array}$ Az egyenletrendszer megoldása: $\begin{array}{c}{\displaystyle \omega =3\mathrm{,}32{\text{ s}}^{-1};v_1=1\mathrm{,}66\text{ m/s};v_2=0\mathrm{,}37\text{ m/s}\mathrm{.}}\end{array}$ A lecsúszó test sebessége: $\begin{array}{c}{\displaystyle v=\sqrt[]{v_1^2+v_2^2}=1\mathrm{,}70\text{ m/s}\mathrm{.}}\end{array}$ $b)$ Egyenletesen gyorsuló mozgás jön létre, $t{v}_2/2=h$, $t=1\mathrm{,}08$ s.   Második forduló   1. feladat. Egy 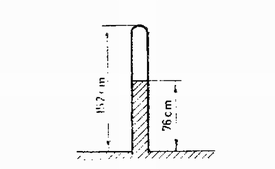$152\text{<span style="font-style: italic;"> cm</span>}$ hosszú, $2{\text{<span style="font-style: italic;"> cm</span>}}^2$ keresztmetszet-területű csőben a higany $76\text{<span style="font-style: italic;"> cm</span>}$ magasan áll, felette légüres tér van $\left(5.\text{<span style="font-style: italic;"> ábra</span>}\right)$. Mennyi a munkavégzés, amikor a csövet lassan ferde helyzetbe hozzuk úgy, hogy végül ${30}^{\circ }$-os szöget zár be a vízszintessel? Az üvegcső tömege $0\mathrm{,}566\text{<span style="font-style: italic;"> kg</span>}$, a higany sűrűsége $13\mathrm{,}6\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mspace width="0.5ex"></mspace><mi>g</mi><mo stretchy="false">/</mo><mi>c</mi><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$, $g=10{\text{<span style="font-style: italic;"> m/s</span>}}^2$.       5. ábra   Megoldás. A feladatban kérdezett munkavégzés az általunk végzett munkát jelenti, amit az energia-, illetve munkatétel alapján határozhatunk meg. Figyelembe kell vennünk a higany és az üvegcső helyzeti energia változását, továbbá a külső levegő által végzett tágulási munkát, hiszen a külső légnyomás hatására telik meg teljesen az üvegcső higannyal a 6. ábrán látható módon. 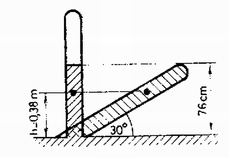    6. ábra   Vegyük észre, hogy a higany súlypontja az üvegcső megdöntése közben nem változik, míg a higany mennyisége végül éppen megkétszereződik, hiszen mire a cső eléri a vízszintessel bezárt ${30}^{\circ }$-os szöget, az üvegcső teljesen megtelik higannyal. A higany tömege: $m_{\text{Hg}}=13\mathrm{,}6{\text{ g/cm}}^3\cdot 2{\text{ cm}}^2\cdot 76\text{ cm}=2\mathrm{,}067\text{ kg}$. A higany helyzetienergia-változása: $\begin{array}{c}{\displaystyle \Delta E_{\text{Hg}}=m_{\text{Hg}}g\cdot h=2\mathrm{,}067\text{ kg}\cdot 10{\text{ m/s}}^2\cdot 0\mathrm{,}38\text{ m}=7\mathrm{,}86\text{ J}\mathrm{.}}\end{array}$ Az üvegcső helyzetienergia-változása: $\begin{array}{c}{\displaystyle \Delta E_{\text{üveg}}=-m_{\text{üveg}}g\cdot h=-0\mathrm{,}566\cdot 10\cdot 0\mathrm{,}38=-2\mathrm{,}15\text{ J}\mathrm{.}}\end{array}$ A külső levegő munkavégzése $\begin{array}{c}{\displaystyle W_{\text{lev.}}=-p\Delta V=-{\varrho }_{\text{Hg}}\cdot g\cdot 2h\cdot \Delta V=-15\mathrm{,}71\text{ J}\mathrm{.}}\end{array}$ Az általunk végzett munka: $\begin{array}{c}{\displaystyle W=+7\mathrm{,}86\text{ J}-15\mathrm{,}71\text{ J}-2\mathrm{,}15\text{ J}=-10\text{ J}\mathrm{.}}\end{array}$ A negatív előjel azt mutatja, hogy a cső magától is eldőlne, a kísérletezőnek vissza kell tartania a csövet döntés közben.   2. feladat. Vízszintes talajon mozgó, $m=1\text{<span style="font-style: italic;"> kg</span>}$ tömegű testnek $v_0=2\text{<span style="font-style: italic;"> m/s</span>}$ kezdősebességet adunk. Induláskor a téglatest $s=1\text{<span style="font-style: italic;"> méter</span>}$ távolságra volt a faltól. A testhez $L=8\text{<span style="font-style: italic;"> cm</span>}$ hosszúságú, $D=100\text{<span style="font-style: italic;"> N/m</span>}$ rugóállandójú rugó van erősítve (7. ábra). A súrlódási együttható $\mu =0\mathrm{,}2$, $g=10{\text{<span style="font-style: italic;"> m/s</span>}}^2$. a) Hol fog a téglatest megállni? b) Mikor fog a téglatest megállni? 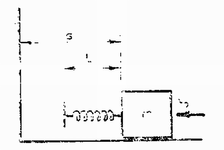    7. ábra   Megoldás. A téglatest rugója $s-L=0\mathrm{,}92$ m megtétele után éri el a falat. Ekkor sebessége $v_1=\sqrt[]{v_0^2-2\mu g\left(s-L\right)}=0\mathrm{,}566$ m/s. Az ehhez szükséges idő: $\begin{array}{c}{\displaystyle t_1=\frac{s-L}{v}=\frac{2\left(s-L\right)}{v_0+v_1}=0\mathrm{,}717\text{ s}\mathrm{.}}\end{array}$ Ezután a test még $x_1$ utat tesz meg a fal felé a megállásig: az $\frac{m\cdot v_1^2}{2}=\mu mg{x}_1+\frac{D}{2}{x}_1^2$ egyenlet alapján $x_1=0\mathrm{,}04$ m. Ezalatt a test olyan rezgést végzett, amelynek körfrekvenciája $\omega =\sqrt[]{D/m}=10{\text{ s}}^{-1}$, amplitúdója $A=x_1+x_0$, ahol $x_0=\mu mg/D=0\mathrm{,}02$ m. Ugyanis a súrlódási erő $x_0$ rugómegnyúlás esetén tart egyensúlyt a rugóerővel. Az amplitúdó $A=0\mathrm{,}04+0\mathrm{,}02=0\mathrm{,}06$ m. Ha az egyensúlyi helyzetből indítanánk ezt a rezgést, akkor a megállásig $T/4=\left(2\pi /\omega \right)/4=0\mathrm{,}157$ s telne el. Azonban nem 0-ból, hanem $t$-ből indul el a negyednél kisebb rezgés, melyet a következő egyenletekből határozhatunk meg: $\begin{array}{c}{\displaystyle x_0=A\cdot \text{sin}\omega t;v_1=A\omega \cdot \text{cos}\omega t\mathrm{.}}\end{array}$ Így $t=0\mathrm{,}034$ s. Az első megállásig tartó idő: $t_2=T/4-t=0\mathrm{,}123$ s. Visszafelé mozogva a súrlódási erő előjelet vált, az egyensúlyi helyzet eltolódik a rugó nyújtatlan helyzetétől balra $x_0$-lal. Az új amplitúdó: $A_1=x_1-x_0=0\mathrm{,}02$ m. Ez azt jelenti, hogy a test egy félperiódus után megáll, akkor a rugó nyújtatlan, a mozgás befejeződik. Ez az időtartam: $t_3=T/2=\pi /10=0\mathrm{,}314$ s. $a)$ A test a faltól 8 cm távolságra áll meg, ekkor a rugó nyújtatlan. $b)$ A teljes mozgási idő: $t_1+t_2+t_3=0\mathrm{,}717+0\mathrm{,}123+0\mathrm{,}314=1\mathrm{,}154\text{ s}$.   3. feladat. Egy hosszú, $R$ sugarú, szigetelő anyagból készült hengerben $r$ sugarú hengeres furat van. A henger és a furat tengelyei párhuzamosak, a tengelyek távolsága $d$ $\left(8.\text{<span style="font-style: italic;"> ábra</span>}\right)$. A szigetelő anyagnak pozitív elektromos töltése van, amelynek térbeli eloszlása egyenletes és sűrűsége $\varrho$. A szigetelő anyag relatív dielektromos állandója $1$. Mekkora az elektromos térerősség a furat belsejében?     8. ábra   Megoldás. A Gauss-tétel alapján könnyen meghatározhatjuk az egyenletesen töltött henger belsejében az elektromos térerősséget. Tekintsünk ugyanis egy hengerszimmetrikusan elhelyezkedő, $h$ magasságú, $x$ sugarú hengerpalástot a hengerben: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle E\cdot 2x\pi \cdot h}& {\displaystyle =\frac{1}{{\epsilon }_0}\varrho x^2\pi h;}\hfill \\ \hfill {\displaystyle E}& {\displaystyle =\frac{\varrho }{2{\epsilon }_0}x\mathrm{,}}\hfill \end{array}}$ vagyis a térerősség a sugárral lineárisan nő, iránya éppen sugárirányú. A furatot úgy is elképzelhetjük, mintha a pozitív töltés mellett ugyanolyan sűrűségű negatív töltést is tartalmazna. Így a furatban a térerősség két, egymáshoz képest eltolt henger terének szuperpozíciójaként áll elő a 9. ábrán szemléltetett módon: $\begin{array}{c}{\displaystyle {\text{<span style="font-weight: bold;">E</span>}}_{\text{furat}}=\frac{\varrho }{2{\epsilon }_0}\text{<span style="font-weight: bold;">x</span>}-\frac{\varrho }{2{\epsilon }_0}\text{<span style="font-weight: bold;">y</span>}=\frac{\varrho }{2{\epsilon }_0}\left(\text{<span style="font-weight: bold;">x</span>}-\text{<span style="font-weight: bold;">y</span>}\right)\mathrm{.}}\end{array}$     9. ábra   Vegyük észre, hogy az $\text{<span style="font-weight: bold;">x</span>}-\text{<span style="font-weight: bold;">y</span>}$ vektorkülönbség éppen a két középpontot összekötő d vektorral egyezik meg, tehát a furatban a térerősség mindenhol d irányú, homogén: $\begin{array}{c}{\displaystyle {\text{<span style="font-weight: bold;">E</span>}}_{\text{furat}}=\frac{\varrho }{2{\epsilon }_0}\text{<span style="font-weight: bold;">d</span>}\mathrm{.}}\end{array}$ Érdemes megjegyezni, hogy ez nem csak henger esetén igaz, hanem például gömb belsejében levő gömb alakú üregben is hasonló homogén tér alakul ki. Ez annak a következménye, hogy egyenletesen töltött gömb belsejében is a sugárral arányos a térerősség.   Kísérleti forduló   A versenyzőknek a Bunsen-féle effúzióméter egyszerűsített modelljével kellett méréseket végezniük. Levegővel és egy ismeretlen gázzal dolgoztak, amelynek relatív molekulatömegét és lehetséges összetételét is meg kellett határozniuk.   Végezetül ezúton is szeretnénk adózni Vermes Miklós tanár úr emlékének, aki sok-sok éven át a fizika OKTV II. és III. kategóriája tantárgyi bizottságának elnöke volt. A fenti feladatsor volt az utolsó, amelyet a bizottság az ő irányításával állított össze, a verseny befejezését halála miatt nem érhette meg.   A verseny végeredménye   I. kategória   1. Hortoványi Ottó (Debrecen, Mechwart A. Gépip. Szki., IV. o. t., t: dr. Kopcsa József), Jávorka László (Pécs, Zipernovszky K. Ip. Szki., IV. o. t., t: Kiss Jenő). 3. Husztek Szabolcs (Miskolc, Kandó K. Ip. Szki., IV. o. t., t: Ambrózy Béla. 4. Németh Tibor (Szombathely, Savaria Közl. Szki., t: Gümdischné Gajzágó Mária). 5. Jakó Attila (Budapest, Latinca S. Szki., III. o.t., t: Pataki Anikó).   II. kategória   1. Boncz András (Zalaegerszeg, Zrínyi M. Gimn., III. o. t., t: Pálovics Róbert). 2. Sándor Balázs (Budapest, Árpád Gimn., IV. o. t., t: Tóth Ibolya). 3. Falus Péter (Budapest, Ságvári E. Gimn., III. o. t., t: dr. Honyek Gyula). 4. Csilling Ákos (Budapest, Fazekas M. Gyak. Gimn., IV. o. t., t: Horváth Gábor). 5. Káli Szabolcs (Budapest, Fazekas M. Gyak. Gimn., IV. o. t., t: Horváth Gábor). 6. Bartsch Tamás (Szeged, Radnóti M. Gimn., IV. o. t., t: Lancsa Jánosné). 7. Czirók András (Miskolc, Földes F. Gimn., III. o. t., t: dr. Zsudel László és Dolák Gabriella). 8. Pusztai Tamás (Kaposvár, Táncsics M. Gimn., IV. o. t., t: Kiss Zoltánné). 9. Szász Róbert (Debrecen, Fazekas M. Gyak. Gimn., IV. o. t., t: Türk Zsuzsanna). 10. Dobler Ervin (Budapest, Fazekas M. Gyak. Gimn., IV. o. t., t: Horváth Gábor).   III. kategória   1. Juhász Attila (Budapest, Apáczai Cs. J. Gimn., IV. o. t., t: Holics László). 2. Rékasi János (Gyöngyös, Berze Nagy J. Gimn., IV. o. t., t: Kiss Lajos). 3. Bodor András (Budapest, Apáczai Cs. J. Gimn., III. o. t., t: Zsigri Ferenc). 4. Horváth Tibor (Kecskemét, Katona J. Gimn., IV. o. t., t: Kocsisné Domján Edit). 5. Molbnár Ingó (Gyöngyös, Berze Nagy J. Gimn., IV. o. t., t: Kiss Lajos). 6. Zóka Gábor (Nagyatád, Ady E. Gimn., IV. o. t., t: Knapp Ottó). 7. Bak János (Dunaújváros, Münnich F. Gimn., IV. o. t., t: Kobzos Ferenc). 8. Táska László (Budapest, Apáczai Cs. J. Gimn., III. o. t., t: Zsigri Ferenc). 9. Pollner Péter (Budapest, Piarista Gimn., IV. o. t., t: Gyimesi István). 10. Buday Gergely (Gyöngyös, Berze Nagy J. Gimn., IV. o. t., t: Kiss Miklós).