Kezdőlap


Cím:	Az 1989. évi Eötvös-verseny
Szerző(k):	Radnai Gyula
Füzet:	1990/február, 81 - 86. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1989. október 20-án rendezte 66. versenyét Budapesten és 12 vidéki városban. A versenyen az 1989-ben érettségizettek és középiskolai tanulók vehettek részt. A feladatok megoldására 5 óra állt rendelkezésre, bármilyen segédeszközt lehetett használni.
Összesen 273 versenyző adott be dolgozatot. A feladatok kitűzését és a beadott megoldások értékelését a Versenybizottság közösen végezte: vezetője Radnai Gyula, tagjai Boros János, Gnädig Péter és Károlyházy Frigyes voltak.
Ismertetjük a feladatokat és a verseny végeredményét.
1. Gergő gyakran segít a háztartásban. A zacskós tejet az 1. ábrán látható módon a zacskónál valamivel szűkebb keresztmetszetű, levágott tetejű és alul kilyukasztott műanyag flakonban szokták tárolni. Gergő megfigyelése szerint a szájával lefelé fordított flakonból a még felbontatlan zacskós tej magától kiesik, viszont a tetejénél megfogott tejes zacskóról még akkor sem esik le a flakon, ha alulról egy másik zacskó tejet akasztunk rá.

1. ábra

Mi lehet a magyarázat?

Megoldás. A flakont a súrlódási erő tartja meg. A súrlódási erő a flakon falára ható nyomóerővel arányos, ez a nyomóerő pedig a tej hidrosztatikai nyomásából származik. A súrlódási erő nagyságát becsléssel állapítjuk meg. Azt kell megmutatnunk, hogy a flakonra ható súrlódási erő az 1. ábrán látható helyzetben

10 N

-nál is nagyobb lehet, viszont a szájával lefelé fordított flakonban a tejeszacskóra

10 N

-nál kisebb súrlódási erő hat.
Most egy becsléssel megmutatjuk, hogy ez teljesül. Az egyszerűség kedvéért mérjük a távolságot centiméterben (2. ábra).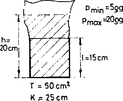

2. ábra

A tejeszacskó kerülete valamivel több, mint 25 cm, ezért a flakonban a zacskó kissé meggyűrődik, így a tej egyenletesen nyomja a zacskót a flakon falához. A zacskóban a tej fölött levegő van, ennek nyomása megközelítőleg egyenlő a külső légnyomással. Esetleg még nagyobb is lehet, ha ‐ miközben tartjuk ‐ jól meg is szorítjuk a zacskót. Ezzel a nyomóerőt és így a súrlódási erőt is tovább növeljük. Most azonban ezt ne vegyük figyelembe; enélkül is meg kell, hogy tartsa a flakont (a ráakasztott másik zacskó tejjel együtt) a súrlódási erő.
Mivel a hidrosztatikai nyomás lefelé lineárisan nő, átlagos értéke a 2. ábra alapján:

\begin{matrix} \bar{p} = \frac{p_{min} + p_{max}}{2} = 1, 25 kPa . \end{matrix}

A flakon falának területe:

\begin{matrix} K \cdot l = 375 {cm}^{2} = 3, 75 \cdot 10^{- 2} m^{2} . \end{matrix}

E kettő szorzatának

μ_{0}

-szorosa adja meg a súrlódási erő maximális értékét. (

μ_{0}

a tapadási-súrlódási együttható, értéke legalább

0, 3

és legfeljebb

0, 6

a zacskó és a flakon fala között.) A legkisebb

μ_{0}

értéket véve is

\begin{matrix} F_{surl} > 13 N, \end{matrix}

tehát a súrlódási erő valóban meg tudja tartani a mintegy

10 N

súlyú másik zacskó tejet.
A feladat megoldása akkor teljes, ha azt is megmutatjuk, hogy a lefelé fordított flakonból magától kiesik a tejeszacskó, még a lehető legnagyobb

μ_{0}

esetén is.
Tegyük fel, hogy a lefelé fordítás után a zacskó még nem mozdult el, csak a tej ömlött át a zacskó alsó részébe (3. ábra).

3. ábra

A flakon falára ható hidrosztatikai nyomás átlagértéke most csak

\begin{matrix} \bar{p} = 0, 5 kPa, \end{matrix}

és ez a kisebb nyomás ráadásul kisebb területen is hat a flakon falára:

\begin{matrix} K l = 250 {cm}^{2} = 2, 5 \cdot 10^{- 2} m^{2} . \end{matrix}

E két érték szorzatának

μ_{0}

-szorosa még

μ_{0} = 0, 6

esetén is csak

7, 5 N

, tehát

\begin{matrix} F_{surl} < 8 N . \end{matrix}

Ezért a tejeszacskó kiesik a lefelé fordított flakonból.

Megjegyzés. A megoldáshoz tartozik

μ_{0}

értékének becslése is. A példaképpen bemutatott gondolatmenetben a

0, 3 ≦ μ_{0} ≦ 0, 6

becslést alkalmaztunk, ez összhangban van a Középiskolai Fizikai Táblázatokban ill. középiskolai és egyetemi tankönyvekben közölt adatokkal. Ugyanakkor, ha a tejeszacskó kívül zsíros,

μ_{0}

jóval kisebb is lehet, s a zsíros tejeszacskóról bizony lecsúszhat a flakon a ráakasztott másik liter tejjel együtt. Most azonban nem erről a tapasztalatról volt szó, nem ezt kellett megmagyarázni.

2. Egy keskeny, hosszú csőben (kapillárisban)

30

mm magasra emelkedik a víz a csövön kívüli szinthez képest. A víz felszíne

30^{\circ}

-os szöget zár be a cső falával az érintkezési vonalnál. A csövet benyomjuk a vízbe (így az teljesen megtelik), majd a felső végén ujjunkkal befogva, függőleges helyzetben egészen kiemeljük a csövet a vízből. Ezután a befogott nyílást újra szabaddá tesszük, s ekkor a víz egy része kifolyik.

4. ábra

Lehet-e a függőleges helyzetű csőben maradó vízoszlop hossza

\begin{matrix} a) & 123 mm; \\ b) & 62 mm; \\ c) & 41 mm; \\ d) & 20 mm? \end{matrix}

Megoldás. Amikor a cső a vízbe nyúlik, (4. ábra)

2 r π α \cdot cos φ

nagyságú erő emeli

h

magasságra az

r^{2} π

keresztmetszetű csőben a vizet:

\begin{matrix} 2 r π α \cdot cos φ = r^{2} π h ϱ g . \end{matrix}

(1)

Jelen esetben

h = 30 mm

φ = 30^{\circ}

, és ha behelyettesítjük a víz sűrűségének és felületi feszültségének táblázati adatait, meghatározhatjuk a kapilláris sugarát:

\begin{matrix} r = 0, 42 mm . \end{matrix}

A sugár kiszámítása nem volt feladat, ezt az adatot nem is fogjuk felhasználni a továbbiakban, viszont segít a kapilláris elképzelésében. Úgy képzeljük, hogy a cső fala elég vékony, még a kapilláris belső átmérőjéhez képest is elhanyagolható a fal vastagsága.
Ebben az esetben amikor kiemeljük a csövet a vízből, a cső alján akkor lép fel a legnagyobb felfelé mutató erő, ha pontosan félgömb alakú, jó közelítéssel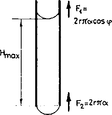

r

sugarú ,,csepp'' alakul ott ki (5. ábra).

5. ábra

Most az egyensúly feltétele:

\begin{matrix} 2 r π α cos φ + 2 r π α = r^{2} π H_{max} ϱ g . \end{matrix}

(2)

Ha az (1) és (2) egyenleteket összevetjük, a csőben maradó vízoszlop maximális hosszára az alábbi egyszerű összefüggés adódik:

\begin{matrix} H_{max} = h \frac{1 + cos φ}{cos φ} . \end{matrix}

Ebbe behelyettesítve a

h = 30

mm és

φ = 30^{\circ}

megadott értékeket:

\begin{matrix} H_{max} = 64, 6 mm . \end{matrix}

Máris kizárhatjuk az a) esetet: a csőben maradó vízoszlop hossza nem lehet 123 mm.

H_{max} = 64, 6

mm-nél rövidebb azonban lehet a vízoszlop hossza, mivel az alsó felület még lehet

r

-nél nagyobb sugarú gömbsüveg, lehet akár vízszintes felület, sőt, lehet olyan is, amely fölfelé domborodik, alulról homorú! Így a csőben maradó vízoszlop akármilyen rövid lehet, tehát

0

és

64, 6

mm között minden hossz lehetséges:

\begin{matrix} 0 ≦ H ≦ H_{max} . \end{matrix}

Ezért a

b)

c)

és

d)

esetben kérdezett hosszak bármelyike megvalósulhat.
A helyes válasz tehát:

a)

nem lehetséges;

b), c), d)

lehetséges.

6. ábra

Megjegyzés: Érdemes külön is megvizsgálni, hogyan alakulhatnak ki az említett felületek a cső alján annak ellenére, hogy az illeszkedési szög mindig

φ (= 30^{\circ})

kell, hogy maradjon! Néhány ilyen esetet rajzoltunk meg a 6. ábrán. Ha nem ilyen vékony a cső fala, hanem ‐ mint az üvegkapillárisok esetén gyakran előfordul ‐ vastagabb, akkor az alul kialakuló csepp alakja elég bonyolult is lehet. Több versenyző szép kvalitatív diszkussziót adott ezekre az esetekre is.

3. Az iskolai

12

V-os,

50

Hz-es váltóáramú áramforrásra sorba kapcsoltunk egy

24

10

W-os izzót és egy

101, 3 μ

F kapacitású kondenzátort. Az izzó alig világít. Rendelkezésünkre áll még egy

0, 1

H induktivitású tekercs is. Hogyan lehetne a kapcsolást úgy átalakítani, hogy az izzó szép fényesen világítson? (A tekercs ohmos ellenállása elhanyagolható. Csak a kapcsolást szabad átalakítani, az alkatrészeket nem.)

Megoldás. A

24 V

10 W

-os izzó ellenállása:

\begin{matrix} R = \frac{{(24 V)}^{2}}{10 W} = 57, 6 Ω . \end{matrix}

101, 3 μ

F-os kondenzátor váltóáramú ellenállása:

\begin{matrix} X_{c} = \frac{1}{ω C} = \frac{1}{314 s^{- 1} \cdot 101, 3 \cdot 10^{- 6} F} = 31, 4 Ω . \end{matrix}

0, 1 H

induktivitású tekercsre:

\begin{matrix} X_{L} = ω L = 314 s^{- 1} \cdot 0, 1 H = 31, 4 Ω . \end{matrix}

Mivel e két váltóáramú ellenállás egyenlő, az embernek azonnal a rezonancia jut az eszébe. Kapcsoljuk sorba mindhárom elemet! Ekkor az eredő impedancia az ohmos ellenállással egyenlő, s erre jut a generátor teljes feszültsége ‐ mégsem ez a legjobb megoldás. Igaz, eredetileg a kondenzátorra és az ellenállásra együtt jutott

12 V

, most pedig magára az ellenállásra egyedül, de hát hol van ez még attól a

24 V

-tól, ami az izzó üzemi feszültsége? Jobban világít az izzó, de ez még nem az igazi.
Ha mindhárom elemet párhuzamosan kapcsoljuk, akkor is csak

12 V

juthat az izzóra.
Térjünk vissza az eredeti ötlethez, a soros rezonancia esetéhez! A sorbakapcsolt tekercsen és kondenzátoron külön-külön sokkal nagyobb lehet a feszültség, mint a generátor feszültsége. Nem lehetne ezt kihasználni?
Kössük sorosan a tekercset és a kondenzátort a generátorra, és kapcsoljuk az izzót valamelyik elemmel párhuzamosan! Mivel eredetileg a kondenzátor és az izzó voltak sorba kapcsolva, a legegyszerűbb az lesz, ha a már összeállított kapcsolásban az izzóra párhuzamosan rákötjük a tekercset (7. ábra).

7. ábra

Hogyan határozhatjuk meg most az izzóra jutó feszültséget?
Az izzóra és a tekercsre ugyanaz a feszültség jut. A tekercsen átfolyó áram negyed periódust (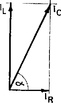

90^{\circ}

-ot) késik ehhez a feszültséghez képest, az izzón átfolyó áram pedig ugyanabban a fázisban van, mint a rá jutó feszültség. Ez azt jelenti, hogy a tekercsen és az izzó ellenállásán átfolyó áram között van

90^{\circ}

fáziskülönbség. A szokásos vektoros ábrázolással még a kondenzátoron átfolyó áramot is megkaphatjuk, mint a kettő vektori összegét (8. ábra).

8. ábra

Az ábra alapján

tg α

értéke:

\begin{matrix} tg α = \frac{I_{L}}{I_{R}} = \frac{R}{ω L} = R ω C . \end{matrix}

Az áramok vektorábráját felhasználva szerkeszthetjük meg a feszültségek vektorábráját. Az ellenálláson a feszültség ugyanolyan fázisú, mint a rajta folyó áram, tehát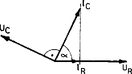

I_{R}

és

U_{R}

vektora ugyanolyan irányú. A kondenzátoron a feszültség

90^{\circ}

-kal van elmaradva a kondenzátoron folyó áramhoz képest, ahogy azt a 9. ábra mutatja.

9. ábra

U_{c}

értéke az ábra alapján:

\begin{matrix} U_{c} = I_{c} \cdot \frac{1}{ω C} = \frac{I_{R}}{cos α} \cdot \frac{R}{tg α} = \frac{U_{R}}{sin α} . \end{matrix}

Ezt az összefüggést felhasználva szerkeszthetjük meg a generátor feszültségének vektorát is (10. ábra).

10. ábra

A 10. ábráról már leolvasható az izzóra jutó

U_{R}

és a generátor

U

feszültsége közti összefüggés:

\begin{matrix} U_{R} = U \cdot tg α = U \frac{R}{ω L} = 12 V \frac{57, 6 Ω}{31, 4 Ω} = 22, 0 V . \end{matrix}

Ekkor már mondhatjuk, hogy a

24 V

-os izzó fényesen világít.
Ugyanilyen jó megoldás az is, ha az izzót a kondenzátorral kötjük párhuzamosan, és velük sorba a tekercset.
Az összes többi esetben az izzóra ennél kisebb feszültség jut.

Megjegyzés. Akik ismerik e vektoros számítás mélyebb hátterét, az ún. komplex formalizmust, azok algebrai úton is kiszámíthatják mindazt, amit a fenti geometriai megoldásból kaptunk. A komplex formalizmusban az áramokat és a feszültségeket olyan komplex számokkal jellemezzük, melyek abszolút értéke adja az áramok és feszültségek csúcsértékét, a valós tengellyel bezárt szög pedig a fázisszöget. A komplex impedanciák:

\begin{matrix} {\tilde{X}}_{L} = j ω L, {\tilde{X}}_{c} = \frac{1}{j ω C}, \tilde{R} = R, \end{matrix}

ahol

j = \sqrt[]{- 1}

komplex egységgyök.
Érdeklődők számára az alapfokú egyetemi és főiskolai elektromosságtani tankönyvek és jegyzetek tanulmányozását javasoljuk.
Hangsúlyozzuk azonban, hogy a feladatot meg lehetett oldani a komplex formalizmus ismerete nélkül is.

Gnödig Péter és Radnai Gyula ismerteti a 3. feladat megoldását

A verseny eredménye

I. díjat kaptak egyenlő helyezésben:

Antal Csaba, a Budapesti Műszaki Egyetem I. éves villamos mérnök hallgatója, aki a budapesti Apáczai Csere János Gimnáziumban érettségizett, mint Flórik György tanítványa, és Rékasi János, a gyöngyösi Berze Nagy János Gimnázium IV. osztályos tanulója, Kiss Lajos tanítványa.

II. díjat kaptak egyenlő helyezésben:

Laux Ádám, a budapesti Táncsics Mihály Gimnázium IV. osztályos tanulója, tanárai Holicsné Csejk Gabriella és Szabó László; Somfai Ellák, az Eötvös Loránd Tudományegyetem I. éves fizikus hallgatója, aki Pápán, a Petőfi Sándor Gimnáziumban érettségizett, mint Dankó Ferenc tanítványa, és Szabó Szilárd, az Eötvös Loránd Tudományegyetem I. éves fizikus hallgatója, aki Budapesten, az Apáczai Csere János Gimnáziumban érettségizett, mint Holics László tanítványa.

III. díjat kaptak egyenlő helyezésben:

Boncz András, a zalaegerszegi Zrínyi Miklós Gimnázium III. osztályos tanulója, Pálovics Róbert tanítványa; Késmárki Szabolcs, a budapesti Műszaki Egyetem I. éves villamosmérnök hallgatója, aki Kecskeméten, a Bányai Júlia Gimnáziumban érettségizett, mint Borsos Ferenc tanítványa, és Kovács Attila, a debreceni Mechwart András Gépipari Szakközépiskola IV. osztályos tanulója, Kopcsa József tanítványa.

Dicséretet kaptak egyenlő helyezésben:

Fülöp Gábor, a budapesti Fazekas Mihály Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa és Horváth Tibor, a kecskeméti Katona József Gimnázium IV. osztályos tanulója, Kocsisné Domján Erzsébet tanítványa.
Az eredményhirdetésre 1989. november 24-én került sor az ELTE Múzeum körúti fizikai előadótermében. A nyertes versenyzőkön és tanáraikon kívül részt vettek az ünnepélyes díjkiosztáson a KöMaL 1988‐89. évi fizika pontversenyének legjobbjai is, akik szintén átvehették díjukat.
Az Eötvös verseny eredményhirdetését a Bolyai Farkas fizikaverseny eredményhirdetése követte. Az Eötvös verseny díjait Kroó Norbert akadémikus, az Eötvös Loránd Fizikai Társulat elnöke, a Bolyai Farkas fizikaverseny díjait Gündischné Gajzágó Mária középiskolai tanárnő, Bolyai Farkas fizikai munkásságának kutatója adta át.
Valamennyi nyertes és helyezett versenyzőnek, valamint az őket felkészítő tanároknak ezúton is gratulálunk.