Cím: 1989. Kürschák József Matematikai Tanulóverseny feladatainak megoldásai
Szerző(k):  Surányi János 
Füzet: 1990/február, 51 - 61. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Adottak az egymást metsző e és f egyenesek és egy kör, amelyiknek nincs közös pontja az egyenesekkel. Szerkesszük meg azt az f-el párhuzamos egyenest, amelyre a körből kimetszett húr aránya az e egyenestől a körig terjedő szakaszhoz a legnagyobb.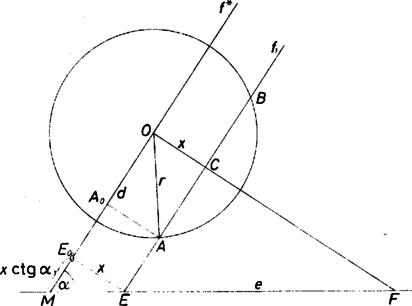

 
 

1. ábra
 

A következő jelöléseket fogjuk használni (lásd az 1. ábrát). A kör középpontja O, sugara r, az O-n át f-fel párhuzamosan húzott egyenes f*, metszéspontja e-vel M, az e és f közti hegyes vagy derékszög α; egy f-fel párhuzamos f1 egyenes metszéspontja e-vel E, a körrel A és B (E,A,B sorrendben); AB felezőpontja C, a CO egyenes metszéspontja e-vel, (ha létezik), F, OC=x, tekintsük pozitívnak, ha C az e és f közti hegyesszögű (illetőleg, ha merőlegesek az egyik) szögtartományban van, negatívnak, ha a másikban; végül OM=d.
 

I. megoldás. A feladatban szereplő szakaszokat kifejezzük a bevezetett mennyiségekkel. AB=2AC=2r2-x2. EA meghatározásához vetítsük E-t és A-t f*-ra, vetületük legyen E0, ill. A0. Ekkor A0A=x, ahol |x|≦r és
EA=E0A0=d-ME0-A0O=d-x ctg α-r2-x2.
A keresett arány tehát
ABAE=2r2-x2d-x ctg α-r2-x2=2d-x ctg αr2-x2-1.
Ez akkor a legnagyobb, ha a nevezőben levő tört a legkisebb értékét veszi fel. Ez a tört pozitív, mert d-x ctg α=E0O=EC és e a körön kívül van, tehát ugyanott veszi fel legkisebb értékét, ahol a négyzete, (d-x ctg α)2/(r2-x2).
Ha x r-hez, vagy -r-hez közeledik, akkor a tört felvesz tetszés szerint nagy értékeket, így legkisebb értékét a számköz belsejében veszi fel, az tehát helyi szélsőérték is, s így ott a tört deriváltja 0. A derivált nevezője pozitív az egész számközben. Számlálója

2(-ctgα)(d-x ctg α)(r2-x2)-(-2x)(d-x ctg α)2==2(d-x ctg α)(dx-r2 ctg α).

Láttuk, hogy az első zárójelben álló mennyiség pozitív, így a derivált a
dx0=r2 ctg α(1)
összefüggésnek eleget tevő helyen tűnik el. Itt negatív értékből megy át pozitívba, tehát a függvénynek itt minimuma van. (Ez egyébként abból is következik, hogy csak egy szélsőérték adódott, egy minimumhelynek viszont kell lennie.)
Többféleképpen is szerkeszthetjük x0-t. Ha x0=0 (azaz α=90∘, e és f merőleges), akkor az O-n át e-re merőlegesen húzott egyenesre a legnagyobb a kérdéses arány (ez egyébként közvetlenül is világos). Ennek szerkesztése közismert.
Ha α hegyes szög, írjuk (1)-et ilyen alakban:
x0r=r ctg αd.(2)

 
 

Messe az OF-nek a körrel való metszéspontján át e-vel párhuzamosan húzott egyenes f*-ot G-ben (2. ábra). Ekkor GO=r ctg α, (2) jobb oldala tehát a GO/MO aránnyal egyenlő. Ezt akarjuk úgy vetíteni, hogy a nevező r hosszúságú szakaszba menjen át. Messe az MO és a kör metszéspontján át MO-ra merőlegesen állított egyenes e-t H-ban, a H-ból OF-re bocsájtott merőleges utóbbit I-ben, végül FG és HI metszéspontja legyen J. Ekkor HI=r, és így a párhuzamos szelők tétele szerint GO/MO=JI/HI=JI/r. A keresett x0 szakasz tehát JI. Ezt felmérve O-ból OF-re és végpontjában merőlegest állítva OF-re kapjuk a keresett egyenest.
 

Megjegyzések: 1. A szelő jellemzésére használhatjuk pl. az AOC szöget, vagy más paramétert is.
2. A (2) jobb oldalán álló törtet tg α-val bővítve az x0/r=r/d ctg α összefüggést kapjuk. Itt d tg α=OF (3. ábra), így a nyert egyenlőségből leolvasható, hogy az AOC és az FOA háromszög hasonló. Az O-nál levő szögük ugyanis közös és egy megfelelő oldalpárjuk aránya egyenlő. Az előbbi háromszög C-nél levő szöge derékszög, tehát az utóbbiban FA merőleges az OA körsugárra. A keresett szelő metszéspontjai a körrel tehát az F-ből húzott érintők érintési pontjai. Ezt nem nehéz közvetlenül belátni.
 
 

II. megoldás: Legyen α hegyesszög. Az f-fel párhuzamos érintőkre az AB/EA arány 0, aminél lehet nagyobb is. Akkor a legnagyobb, amikor az AC/EA arány, ez pedig akkor, amikor a reciproka a legkisebb. Azt még 1-gyel növelve az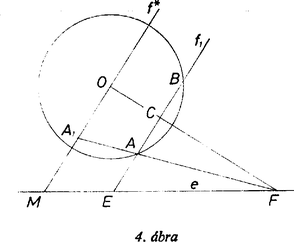
EAAC+1=EA+ACAC=ECAC
arány minimumát szolgáltató szelőt keressük.
 
 

FA és MO metszéspontját A1-gyel jelölve EC/AC=MO/A1O (4. ábra). Itt a számláló nem függ a szelő helyzetétől, így az arány akkor a legkisebb, amikor a nevező a legnagyobb, ez pedig az F-ből húzott érintő érintési pontjára teljesül.
Az F-ből húzott érintők érintési pontját az OF átmérőjű kör metszi ki az adott körből.
 
 

5. ábra
 

Legyen most f1 ezeken a pontokon átmenő szelő, f' egy másik, és azon E',A',C' a megfelelő metszéspontok, A* pedig az FA-val való metszéspont (5. ábra). Ekkor
E'A'>E'A*,A'C'<A*C',  tehát  A'C'/E'A'<A*C'/E'C',
vagyis a feladatban kérdezett arány valóban a megszerkesztett egyenesen a legnagyobb.
Ha e és f merőleges, akkor f*-ra lesz EB a lehető legnagyobb, EA pedig a legkisebb, tehát a vizsgált arány a legnagyobb. Ennek az egyenesnek a szerkesztése közismert.
 

Megjegyzések. 1. Okoskodhatunk a következő módon is. Tetszés szerinti f1 szelőt véve, a kört egy OF tengelyű és EC/AC arányú merőleges affinitás olyan ellipszisbe viszi át, amelyiknek van közös pontja e-vel. Ha van az ellipszisnek pontja az e-nek a kört nem tartalmazó partján is, akkor az F-ből húzott egyik érintő is ezen az oldalon van, és annak az érintési pontját egy kisebb arányú affinitás viszi át e-re (6. ábra).
 
 

6. ábra
 

Az arány tehát akkor a legkisebb, ha az e-t érintő ellipszist kapjuk, vagyis e az F-ből a körhöz húzott érintő képe. Arra a szelőre lesz tehát a nyújtás aránya a legkisebb, s így a feladatban kérdezett arány a legnagyobb, amelyik az F -ből húzott érintő érintési pontján megy át. Ezen az úton oldotta meg a feladatot Újváry-Menyhárt Zoltán.
2. Gerlits Ferenc számítással oldotta meg a feladatot, de az analízis használata helyett csak a másodfokú egyenletekre vonatkozó ismeretekre támaszkodva.
 

III. megoldás. Az I. megoldásban láttuk, hogy azt az x értéket kell megkeresnünk, amelyikre a (d-x ctg α)2r2-x2=c arány a legkisebb. Más szóval a legkisebb c-t, amelyikre a
(c+ctg2α)x2-(2d ctg α)x+d2-cr2=0
egyenletnek van megoldása, annak abszolút értéke r-nél kisebb és c pozitív. Az egyenletnek akkor van (valós) megoldása, ha nem negatív a diszkriminánsa. A diszkrimináns
4(d2 ctg2α-(c+ctg2α)(d2-cr2))=4c(cr2-(d2-r2ctg2α)).
Ez kell, hogy ne legyen negatív. Mivel c-nek pozitívnak kell lennie, tehát a második tényező sem lehet negatív. Innen
c≧(d2-r2 ctg2α)/r2.
Ha ezt a kritikus értéket beírjuk az egyenletbe, az
((d/r)x-r ctg α)2=0
alakra hozható. Ez az I. megoldásban nyert, r-nél kisebb x0 értéket szolgáltatja.
 

IV. megoldás. Húzzunk A-n át párhuzamost e-vel, messe ez a kört másodszor D-ben. Ha érintőt kapunk, akkor D=A (7.a, b, c ábra).
 
 

7.a ábra
 

 
 

7.b ábra
 

 
 

7.c ábra
 

Ekkor a rövidebb BD ívet α szögű (esetleg csúcs-) szögtartomány foglalja magába, így a BD húr hossza csak α-tól függ, az AB szelő helyzetétől nem. BD és e metszéspontját G-vel jelölve a párhuzamos szelők tétele szerint AB/EA=DB/GD. Ez tehát akkor a legnagyobb, ha GD a legkisebb, egyúttal, BD állandó volta miatt GB is, s így GD⋅GB, ami G hatványa a körre, szintén a legkisebb. Ez a szorzat minden G-n átmenő szelőre ugyanakkora, így az O-n átmenőre is. Ennek a körbe eső húrja átmérő, független a G pont helyzetétől, így a hatvány az e egyenesnek a körhöz legközelebb eső pontjára, O-nak e-n való T merőleges vetületére lesz a legkisebb. Az ezt szolgáltató, f-fel párhuzamos egyenest kell tehát megszerkesztenünk.
Az egyenlő hosszúságú húrok egy O középpontú (rcosα sugarú) kör érintői. Ehhez a körhöz megszerkesztjük T-ből a két érintőt. Mindkettőnek a T-től távolabbi metszéspontját a másik közelebbi metszéspontjával kötve össze, két egyenest kapunk (8. ábra), amelyek α nagyságú szöget zárnak be e-vel egyik, illetőleg másik irányban. Egyikük tehát párhuzamos f-fel. A követett gondolatmenet megfordításával látható, hogy ez valóban a keresett egyenes.
Ezt a megoldást Fleiner Tamás adta.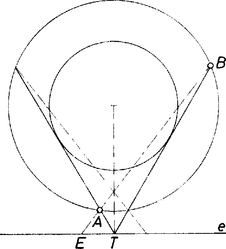
 
 

8. ábra
 

V. megoldás. Ismét deriváltat használunk, de kiszámítása helyett geometriai jelentéséből vonunk le következtetéseket.
Legyen α hegyesszög. Koordinátatengelyeknek válasszuk az O-n átmenő, f-re merőleges és a vele párhuzamos egyenest. Ekkor CA az OC=x változónak azt a -r≦x≦r számközön értelmezett g függvényét szemlélteti, amelyiknek a képe a tengely fölötti félkör, AE pedig ugyanezen a szakaszon azt a h függvényt, amelyre g+h képe az e egyenesnek a szakasz feletti része. A g/h függvény legnagyobb értékét keressük.
Ez a függvény értelmezve van az egész számközön, mivel e-nek nincs közös pontja a körrel, s így a nevező nem 0. A végpontokban a hányados értéke 0, máshol pozitív, így maximuma helyi maximum is, ott a derivált 0, s így annak számlálójára:
g'h-gh'=0(3)
teljesül. Itt g' a kör A-ban húzott érintőjének az iránytangense, h' pedig a (g+h)'=g'+h' összefüggésből kapható. Itt ugyanis a bal oldalon az e egyenes iránytangense, tg α áll, tehát
h'= tg α-g'.
Innen látjuk, hogy a két derivált nem lehet egyszerre 0, tehát (3) csak úgy teljesülhet, ha egyik sem 0.
 
 

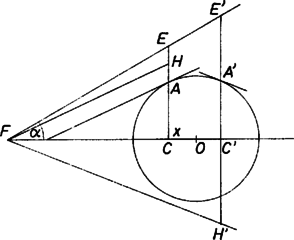9. ábra
 

Húzzunk F-ből párhuzamost az A-ban húzott érintővel (9. ábra), jelöljük CA-val való metszéspontját H-val. Ez a tartomány belsejében levő C pontokra mindig létezik. Ekkor  tg α=CE/FC, az érintő iránytangense CH/FC (negatív, ha H a tengely alatt van), így h'=CE/FC-CH/FC=HE/FC (negatív, ha H az e egyenes fölött van).
Írhatjuk (3)-at, mivel fennállása esetén a deriváltak nem tűnhetnek el, g'h'=g/h alakban. A jobb oldali arány CA/AE-vel egyenlő, a bal oldalon álló pedig megállapításaink szerint a következővel:
CHFCHEFC=CHHE.
Rögzített C és E pontok mellett a CE egyenes különböző P pontjaira a CP/PE arány különböző, ha előjeles arányt nézünk, mint esetünkben. A (3) egyenlőség tehát csak akkor állhat fenn, ha H=A, vagyis az F-en át az A-beli érintővel párhuzamosan húzott egyenes átmegy A-n, azaz A az F-ből a körhöz húzott érintő érintési pontja. Ezzel először is azt kaptuk, hogy a törtnek egy szélsőértéke van, mivel pedig kell egy maximumának lennie, így ez a szélsőérték maximum. Azt is kaptuk, hogy ezt az F-ből a körhöz húzott érintő érintési pontján átmenő egyenes szolgáltatja.
 
Megjegyzés. A bizonyítás szellemes alapötlete Bodor András dolgozatában található. Számos, analízisbeli eszközöket használó megoldással ellentétben a megoldás geometriai tartalmát mutatja meg. Ez természetesen egyszerűbben nyerhető elemi úton, mint pl. a II. megoldásban láttuk.
 

2. Adott pozitív egész n-re jelölje S(n) a tízes számrendszerben felírt n szám jegyeinek az összegét. Melyek azok az M pozitív egész számok, amelyekre S(Mk)=S(M) minden olyan k egészre, amelyre 1≦k≦M?
 

I. megoldás. M=1 természetesen megfelel, mivel k csak 1 lehet. Nagyobb M-ekre nézzük meg a k=2 választást. Tudjuk, hogy egy szám 9-cel osztva ugyanannyi maradékot ad, mint a számjegyeinek az összege. Így
9|M-S(M),és9|2M-S(2M),
amiből, különbségüket képezve,
9|(2M-S(2M)-(M-S(M))=M-S(2M)+S(M)=M.
A feladat feltétele tehát az 1-en kívül csak 9-cel osztható számokra teljesülhet.
Tegyük fel, hogy M egy n-jegyű szám, amelyre teljesül a feladat feltétele:
10n-1≦M<10n,
és első jegye a(≧1), M=a10n-1+A, ahol A legfeljebb (n-1) jegyű. (Lehet 0 is; ha n=1, akkor csak az lehet.) Mivel M osztható 9-cel, így nagyobb 10n-1-nél, tehát k választható 10n-1+1-nek. Ekkor
kM=(10n-1+1)M=10n-1(M+a)+A.
Az első tag (n-1) darab 0-val végződik, a második legfeljebb (n-1)-jegyű, tehát az összeadásnál minden jegyét 0-hoz kell adni. A számjegyösszeg tehát a két tag jegyösszegének az összege.
Az első tag jegyösszegét a végén álló nullák nem befolyásolják, így annak jegyösszege S(M+a). A jegyei azonosak M jegyeivel, a kivételével, így S(A)=S(M)-a. A feladat feltétele tehát akkor teljesül, ha S(M+A)=a.
Ha M+a is n-jegyű, akkor első jegye vagy a, és ekkor van még 0-tól különböző jegye, mivel nagyobb M-nél, vagy pedig a+1 az első jegye. Jegyösszege mindkét esetben nagyobb a-nál. Ha M+a(n+1)- jegyű, tehát legalább 10n, akkor
10n>M≧10n-a≧10n-9,
ebbe a számközbe pedig csak egy 9-cel osztható szám esik: 10n-1, vagyis az n darab kilencessel írt szám. (n tetszőleges pozitív egész szám.)
Megmutatjuk, hogy az ilyen alakú számok megfelelnek. Legyen M=10n-1 és 2≦k≦M. Ekkor
kM=(k-1)10n+10n-k=(k-1)10n+(10n-1)-(k-1).
Itt az első tag n darab 0-val végződik, a második az n darab kilencessel írt szám, a kivonandó pedig legfeljebb n-jegyű. Így a jegyösszeg ismét az első tag jegyösszegének és a különbség jegyösszegének az összege. Az első tag jegyösszege S(k-1), a különbség képzésénél pedig k-1 minden jegyét 9-ből kell levonni, tehát átvitelre nem kerül sor. Így a különbség jegyösszege 9n-S(k-1). kM jegyösszege tehát 9n, ami megegyezik S(M)-mel. Ezt akartuk belátni.
 

II. megoldás. Az előző megoldásból átvesszük azt, hogy csak 9-cel osztható számok jönnek szóba, és hogy az 1 és a 10n-1 alakú számok megfelelnek. Ezekre támaszkodva látjuk be, hogy ezek már megadják az összes megfelelő számot.
Legyen M egy 1-nél nagyobb megfelelő szám. Legyen hozzá n az a pozitív egész, amelyre (10n-1)/9≦M<(10n+1-1)/9. Az alsó korlátot választva k-nak
S(kM)=S((M/9)(10n-1)).
Itt M/9<(10n+1-1)/81<(10n-1). Mivel (10n-1)-re teljesül a feladat feltétele,
S(M9(10n-1)=S(10n-1)=9n.
Ha M n-jegyű, akkor ez csak úgy egyezhet meg S(M)-mel, ha M az n darab kilencessel írt szám, 10n-1. Ha M (n+1)-jegyű, akkor első jegye csak 1 lehet és a további jegyei közt kell 0-nak lennie, mert kisebb a csupa egyessel írt számnál. Ekkor azonban jegyösszege legfeljebb 1+9(n-1)<9n volna. A feltételnek tehát valóban csak a mondott számok felelnek meg.
Ez Fleiner Tamás megoldása.
 

Megjegyzések: 1. Ugyanígy adódik tetszés szerinti b alapú számrendszer esetén, hogy az 1 és a csupa (b-1)-es jeggyel írt számok a kívánt tulajdonságúak.
2. Láttuk, hogy a 9-cel nem osztható számok már k=2-re sem elégítik ki a megkívánt egyenlőséget. Nem látszik azonban könnyű kérdésnek, hogy egy 9-cel osztható számhoz melyik a legkisebb k, amelyiknél ez bekövetkezik. A II. megoldás valamivel nagyobb k-ra mutatja ezt meg, mint az I. Sok számhoz található, azonban annál is jóval kisebb "rossz'' k érték. Már a 2 ilyen pl. 324-hez, a 3 a 126-hoz, a 4 a 117-hez, az 5 a 351-hez, a 6 a 189-hez, viszont 198-hoz az I. megoldás szolgáltatta 101 a legkisebb k érték. Nem nagyon látszik, hogy ez a legkisebb k érték a szám milyen tulajdonságaitól függ.
 

3. A koordinátasíkban egy tetszőleges pontból egy lépésben vagy az abszcisszája kétszeresével mehetünk fel vagy lefelé, vagy pedig az ordinátája kétszeresével jobbra vagy balra. Egyik lépés után sem szabad azonnal visszalépni.
Bizonyítsuk be, hogy ha az (1,2) pontból indulunk, akkor oda véges sok lépésben nem tudunk visszajutni.
 

I. megoldás. Figyeljük meg: ha az (a,b) pont nincs egyik tengelyen sem, és |a|≠|b|, akkor a négy lehetséges lépés közül háromban távolodunk az origótól, a negyedikben közeledünk hozzá.
 
 

10.a ábra
 

 
 

10.b ábra
 

Valóban, két lehetséges lépés a megfelelő koordináta abszolút értékét növeli, s mivel a másik koordinátát nem változtatja, így az origótól való távolságot is növeli. Ha a kisebb abszolút értékű koordináta abszolút értékének csökkentése irányába indulunk (10.a és 10.b) ábra), akkor már a másik koordináta egyszeresével lépve a megfelelő tengely ellenkező oldalára kerülünk, majd még növeljük az abszolút értéket a nagyobb abszolút értékű koordinátáéval, így ennek a koordinátának az abszolút értéke növekszik. A negyedik esetben a nagyobb abszolút értékű koordináta csökkentése irányában a másik egyszeresével lépve az abszolút érték csökken. Továbblépve lehet, hogy tovább csökken, de most már növekedhet is, ha a tengely ellenkező oldalára kerülünk, azonban kisebb lesz, mint a kisebb koordináta-abszolútérték volt, tehát eredeti értékéhez képest csökken. Ez esetben tehát közeledünk az origóhoz.
Jegyezzük még meg, hogy ha a koordináták aránya nem racionális, akkor továbblépés után sem válhat azzá, így egyik sem lesz 0, és egyenlőkké sem válnak. Ez teljesül a feladatban adott pontra is.
Azt bizonyítjuk be indirekt úton, hogy ha egy pont egyik koordinátája sem racionális számszorosa a másiknak, akkor abból indulva véges számú lépésben nem térhetünk oda vissza. Tegyük fel, hogy véges sok lépésben visszaérnénk. Utolsó megjegyzésünk szerint egyik pont sincs koordinátatengelyen és koordinátáik abszolút értéke különböző. Ha az első lépésben távolodunk az origótól, akkor legyen Pk az útnak az origótól legtávolabbi pontja, vagy az ilyenek egyike, és Pk-1 az út mentén előtte levő pont, Pk+1 a következő. A feltevés szerint mindkettő közelebb van az origó-hoz, mint Pk, így utóbbi ismeretében egyértelműen meg van határozva, hogy melyik pont a Pk+1. Azonban Pk-ból megengedett lépés visz Pk-1-be is, és ezzel is közeledünk az origóhoz. Így a Pk-val szomszédos pontok egybeesnek. Ez viszont nem megengedett.
Lehetséges volna még, hogy a P1-be vezető e]ső lépés közelebb vigyen az origóhoz. Ekkor P1 koordinátáinak aránya sem racionális és innen visszalépve a kiindulási pontba, majd az oda visszavezető utat fordított irányban téve meg, de csak P1-ig, olyan lépéssorozatot kapunk, amelyik ebből a pontból tér ide vissza. Ez már az origótól való távolodással indul. Ez azonban a fenti gondolatmenet szerint nem lehetséges. Semmilyen véges lépéssorozattal nem juthatunk tehát vissza kiindulási pontunkba.
 

II. megoldás. Egy u+v2 alakú számnál, ahol u és v racionális, u és v egyértelműen meg van határozva. Ha ugyanis
p+r2=s+t2,azaz(r-t)2=s-p,
akkor r=t, mert különben 2-re racionális érték adódnék, azonban 2 nem racionális; ekkor pedig p=s. Az (1,2) pontból kiindulva minden pont koordinátái u+v2 alakúak valamilyen egész u és v számmal. (Nevezzük u-t a szám egész összetevőjének.) Valóban, az (u+v2, w+z2) pontból tovább lépve világos, hogy a megváltozó koordináta újra ilyen alakú lesz.
Figyeljük meg azt is, hogy az itt szereplő egészek páros vagy páratlan volta sem változik meg, mert mindegyiket páros egésszel változtatjuk meg.
Ugyancsak világos, hogy az (u,w) és a (v,z) párok külön-külön a feladatban szereplő előírások szerint változnak, egymást nem befolyásolják.
Egy pontból kiindulva oda nem érhetünk vissza, ha mindig csak az egyik tengely irányában haladunk, az azonnali visszalépés tilalma miatt. Így az (1, 2) pontból indulva változtatni kell valamikor az ordinátát is, ha vissza akarunk jutni. Azaz a koordináták egész összetevőjének (1,0)-ról valamikor (1, 2e)-re kell változnia, ahol e vagy 1, vagy -1. Ezeket az egész összetevőket tekintve a továbbiakban koordinátáknak és a most említett lépést első lépésnek, azt mutatjuk meg teljes indukcióval, hogy a koordináták abszolút értékének a nagyobbika minden lépésben nő, és a következő lépésben a nagyobb abszolút értékű koordinátát csak úgy változtathatjuk, hogy az abszolút értéke növekedjék. Ebből következik a feladat állításának helyessége, mert ahhoz, hogy az (1,2) pontba visszajussunk, az egész összetevők maximumának 1-nek kellene lennie, de ez már az első lépés után 2 lett.
 

Az első lépésben a maximum 1-ről 2-re változott, és mivel az ordináta változott 0-ról 2e-re, ha ezt változtatjuk, a visszalépés tilalma miatt csak 4e-re változtathatjuk. Tegyük most fel, hogy a k-adik lépésben a feltételek teljesülnek. Ha a (k+1)-edik lépésben a nagyobb abszolút értékű koordinátát változtatjuk, akkor az indukciós feltevés szerint ennek abszolút értékét növelnünk kell. Ezzel a maximum is növekszik, és ha a következő lépésben is ezt a koordinátát változtatjuk, akkor csak az abszolút érték növelése irányában szabad. Ha viszont a kisebb abszolút értékű koordinátát változtatjuk, akkor a bevezetőben adott elemzésben láttuk, hogy bármelyik irányba is mozdulunk, ennek a koordinátának az abszolút értéke válik nagyobbá, és ha a következő lépést is ennek a koordinátának az irányába tesszük, akkor csak az abszolút érték növelése irányában léphetünk tovább. Ezzel állításunkat bebizonyítottuk.
 

Megjegyzés. Hasonló gondo]atmenettel bizonyítható az is, hogy az abszolút értékek minimuma nem csökkenhet.
 

III. megoldás. Az előző megoldásban abból következtettünk a feladat állításának a helyességére, hogy ha az (1, 0) pontból elindulva egyszer elmozdulunk a tengelyről, akkor a koordináták abszolút értékének a maximuma mindig nő. Ezt most indirekt úton látjuk be.
Induláskor az első koordináta páratlan, a második páros, így ez minden lépés után is így lesz, mert minden koordináta csak páros egésszel változhat. A két koordináta abszolútértéke tehát mindig különböző.
Tegyük fel, hogy valamelyik lépésben nem növekedne a koordináták abszolút értékének a maximuma. Ekkor keressük meg az első ilyen lépést. Legyen a kiinduló pont nagyobb abszolút értékű koordinátája a, a másik b. A lépés csak a változtatása, és pedig abszolút értékének csökkentése lehet, mert láttuk, hogy ha b-t változtatjuk, akkor ennek abszolút értéke |a|-nál nagyobb lesz, és ez igaz akkor is, ha a abszolút értékét növeljük.
Az előző lépésnek növelésnek kellett lennie. A visszalépés tilalma miatt ez nem történhetett az a koordináta irányában. Ha a b-2ea koordináta változott b-re, ahol e=1, vagy e=-1, ez a lépés csak úgy lehet növekedés, ha a különbség valóban kivonást jelöl. A különbség abszolút értéke ekkor 2|a|-|b|, és ez nem lehet nagyobb, mint |b|. Ebből azonban az következik, hogy |a|≦|b|, előbbi megállapításunkkal ellentétben. A koordináták abszolút értékének maximuma tehát minden lépésben növekszik.