Kezdőlap


Cím:	A Téli Ankét 1. és 6. feladatának megoldása (1990.)
Szerző(k):	Nagypál Éva
Füzet:	1990/április, 153 - 155. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Az $A B C$ háromszög területe $t$ , köré írt körének sugara $R$ , a belső szögfelezők a kört rendre az $A'$ , $B'$ , $C'$ pontokban metszik. Az $A' B' C'$ háromszög területe $T$ . Bizonyítsuk be, hogy $16 T^{3} \geq 27 R^{4} t$ . (A XXX. Nemzetközi Diákolimpiára javasolt feladat, Csehszlovákia.)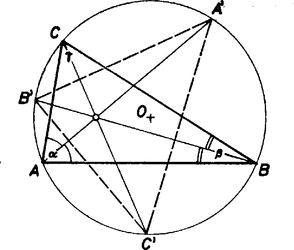

Az ábrán látható jelöléseket használva belátható, hogy

A' C' C ∢ = A' A C ∢ = \frac{α}{2}

, illetve

B' C' C ∢ = B' B C ∢ = \frac{β}{2}

, mivel ugyanahhoz a húrhoz tartozó kerületi szögekről van szó, és

A A'

, ill.

B B'

szögfelezők.
Így

A' C' B' ∢ = A' C' C ∢ + B' C' C ∢ = \frac{α + β}{2}

. Hasonló módon

C' B' A' ∢ = \frac{α + γ}{2}

és

B' A' C' = \frac{β + γ}{2}

Ennek alapján ‐ felhasználva a háromszög területére vonatkozó ismert összefüggést ‐

\begin{matrix} T = \frac{R^{2}}{2} (sin (α + β) + sin (α + γ) + sin (β + γ)) . \end{matrix}

A B C

háromszög területét

t = 2 R^{2} sin α sin β sin γ

alakban felírva a bizonyítandó egyenlőtlenség egy trigonometrikus egyenlőtlenséggé alakítható:

\begin{matrix} 16 {[\frac{R^{2}}{2} (sin (α + β) + sin (α + γ) + sin (β + γ))]}^{3} \geq 27 R^{4} 2 R^{2} sin α sin β sin γ . \end{matrix}

Megfelelő egyszerűsítések, ill. átrendezés után, és felhasználva a

sin (α + β) = sin γ

sin (α + γ) = sin β

és

sin (β + γ) = sin α

összefüggéseket, kapjuk a

\begin{matrix} \frac{sin α + sin β + sin γ}{3} \geq \sqrt[3]{sin α sin β sin γ} \end{matrix}

egyenlőtlenséget. Erről könnyen látható, hogy igaz, mivel

sin α

sin β

és

sin γ

pozitív számok (egy háromszög szögeinek szinuszai), így igaz rájuk a számtani és mértani közép közötti összefüggés.
A megoldásból következik, hogy egyenlőség akkor áll fenn, ha

sin α = sin β = sin γ

, azaz a háromszög szabályos.

(Nagypál Éva Szeged, Ságvári E. Gyak. Gimn., III. o. t.)

6. Bizonyítsuk be, hogy ha

a < b

, akkor

a^{3} - 3 a \leq b^{3} - 3 b + 4

(

a, b

valós). Teljesülhet-e az egyenlőség? (A XXX. Nemzetközi Diákolimpiára javasolt feladat, Svédország.)

I. megoldás. Bevezetve az

f (x) = x^{3} - 3 x

jelölést, a bizonyítandó állítás (mivel

a < b

f (a) \leq f (b) + 4

. Vizsgáljuk az

f (x)

függvényt!
Ennek a függvénynek a differenciálhányadosa egy tetszőleges

x

pontban,

x_{n} \to x

(

x_{n} \neq x

\begin{matrix} f' (x) = \frac{f (x) - f (x_{n})}{x - x_{n}} = \frac{x^{3} - 3 x - x_{n}^{3} + 3 x_{n}}{x - x_{n}} \to 3 (x^{2} - 1) . \end{matrix}

Ebből látható, hogy a differenciálhányados a

[- 1,1]

intervallumon negatív, a [

- \infty

- 1

] és az [1,

\infty

] intervallumon pedig pozitív. Azaz az

f (x)

függvény a

[- 1,1]

intervallumon monoton csökkenő, ezen kívül monoton növekvő, lokális szélsőértékei a

(- 1)

-ben, illetve az

x = 1

-ben vannak. Ezek alapján 3 esetet különböztetünk meg:

I. eset:

a < b \leq - 1

Ekkor

f (a)

és

f (b)

is az

f

függvény [

- \infty

- 1

] monoton növekvő intervallumában van, így

f (a) \leq f (b)

, azaz

f (a) < f (b) + 4

II. eset:

1 < a < b

Hasonlóan mint az előbb látható, hogy

f (a) < f (b) + 4

III. eset:

a \leq - 1

és

b \geq 1

Ekkor az egyes intervallumokbeli monotonitás alapján

f (a) \leq f (- 1)

, illetve

f (b) \geq f (1)

. Így

f (a) - f (b) \leq f (- 1) - f (1) = 4

. Ebből

f (a) \leq f (b) + 4

.
A megoldásokból következik, hogy egyenlőség akkor áll fenn, ha

a = - 1

és

b = 1

II. megoldás. Mivel

a < b

, ezért bevezethetjük a

b = a + k

jelölést, ahol

k

egy nem negatív valós szám. Ekkor az állítás:

\begin{matrix} a^{3} - 3 a \leq {(a + k)}^{3} - 3 (a + k) + 4. \end{matrix}

Elvégezve a köbreemelést, megfelelő egyszerűsítések után a következő egyenlőtlenséget kapjuk:

\begin{matrix} 0 \leq 3 k a^{2} + 3 k^{2} a + k^{3} - 3 k + 4. \end{matrix}

Osszuk el

3 k

-val, és alakítsuk át az

a

-t tartalmazó tagokat teljes négyzetté:

\begin{matrix} 0 \leq {(a + \frac{k}{2})}^{2} + \frac{k^{3} - 3 k + 4}{3 k} - \frac{k^{2}}{4} . \end{matrix}

Ebből, felhasználva, hogy

{(k - 2)}^{2} (k + 4) = k^{3} - 12 k + 16

, a

\begin{matrix} 0 \leq {(a + \frac{k}{2})}^{2} + \frac{{(k - 2)}^{2} (k + 4)}{12 k} \end{matrix}

egyenlőtlenséget kapjuk, amiről könnyen látható, hogy igaz, mivel a jobb oldalon a négyzetes tag mellett egy nemnegatív tag áll. (

k

nem negatív!)

Egyenlőség akkor állhat fenn, ha

{(a + \frac{k}{2})}^{2} = 0

és

\frac{{(k - 2)}^{2} (k + 4)}{12 k} = 0

, amiből

k = 2

a = - \frac{k}{2} = - 1

és

b = a + k = 1

(Nagypál Éva, Szeged, Ságvári E. Gyak. Gimn., III. o. t.)