Cím: Pontszámsejtés a véges geometriákban
Szerző(k):  Reiman István 
Füzet: 1990/december, 435 - 442. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Gyakori jelenség a matematika történetében, hogy egy-egy témaköre több olyan szálból fonódik össze, amelyek indulásukkor még alig mutatnak közös vonásokat; csak a későbbi kutatások fényében derül ki, hogy ugyanannak a nagyobb kérdéskörnek egy‐egy részét alkotják. Ez a helyzet a véges geometriák problémakörével is, amelyek egységbefoglalása és intenzívebb művelése századunk második negyedében indult meg.
Az 1770-es évek végén L. EULER-nek tették fel a következő kérdést:
Egy díszszemlére hat különböző regimentből 6-6 tisztet rendelnek fel: (mai rangmegnevezéssel) egy hadnagyot, egy főhadnagyot, egy századost, egy őrnagyot, egy alezredest és egy ezredest. Hogyan kell a 36 tisztet 6 sorban és 6 oszlopban úgy elhelyezni, hogy minden sorban és minden oszlopban minden regimentből és minden rangból pontosan egy legyen közülük?
EULER nem tudta megoldani ezt a feladatot; az volt a sejtése, hogy ilyen elrendezés nem létezik, sőt akkor sem, ha a regimentek száma 4n+2 alakú és minden regimentből 4n+2 tiszt jön, azaz  6,10,14,...
Jóval később, 1900-ben sikerült G. TARRY-nak bebizonyítania meglehetősen hosszadalmas módon hogy a 36 tiszt feladata megoldhatatlan; bizonyítását azóta már lényegesen egyszerűsítették. Vizsgáljuk most meg kissé közelebbről ezt a feladatot, de hogy áttekinthetőbb legyen, csak 3 regiment 3-3 tisztjére fogalmazzuk meg. Jelölje a tiszti rangokat rendre 0r,1r,2r, a regimenteket 0g,1g,2g. Rendezzük el a tiszteket először a rangjuk (I. táblázat), majd a regimentjük szerint (II. táblázat), az egyes elrendezéseknél csak egy szempontot érvényesítünk:

0r1r2r0g2g1g(0,0)(1,2)(2,1)1r2r0r1g0g2g(1,1)(2,0)(0,2)2r0r1r2g1g0g(2,2)(0,1)(1,0)

 

I. táblázat   II. táblázat    III. táblázat

 
Egy ilyen táblázat már önmagában is érdekes; lényeges tulajdonsága, hogy egy n×n-es négyzet soraiba és oszlopaiba úgy írjuk be a 0,1,2,...,n-1 számokat, vagy a nekik megfelelő szimbólumokat, hogy minden sorban és minden oszlopban egy szám csak egyszer szerepeljen. Az ilyen tulajdonságú elrendezéseket n -edrendű latin négyzeteknek nevezzük. Latin négyzetet nyilván tetszőleges n esetén tudunk szerkeszteni, sőt számuk meglehetősen nagy. A latin négyzetek szerepet kapnak a kombinatorikán kívül az algebrában is; latin négyzet pl. egy csoport műveleti táblázata (szorzótábla). Legegyszerűbb előállítási módja az I. táblázatban látható : minden sort az előzőhöz képest ciklikusan eggyel eltolunk.
Helyezzük most egymásra a két táblázatot; a III. táblázatban levő számpárok első tagja a rangot, a második a regimentet jelöli. Megfigyelhetjük, hogy ez a táblázat megfelel a tisztekre kirótt feltételeknek. Ez lényegében azon múlik, hogy a táblázatba írt 9 számpár különböző, ami azzal egyenértékű, hogy a (0,1,2) elemekből készített összes lehetséges számpár szerepel a táblázatban. A (2,1) számpár pl. azt jelenti, hogy a 2r rangú tiszt az 1g regimentből áll a szóban forgó helyen; az elrendezés akkor lenne rossz, ha ugyanannak a tisztnek két különböző helyen is kellene állnia, ill. ha nem lenne benne minden tiszt az alakzatban.
Ha két latin négyzet olyan, hogy egymásra helyezve a rendezett párok mind különbözők, akkor a latin négyzetek ortogonálisak.
A 36 tiszt feladatának a megoldhatatlansága azt jelenti, hogy nincs két 6-odrendű ortogonális latin négyzet; ha két latin négyzetet egyesítünk, mindig kapunk azonos számpárokat. EULER-nek a 4n+2-rendű ortogonális latin négyzetekre vonatkozó általános jellegű sejtése azonban nem bizonyult igaznak. Nagy érdeklődést váltott ki, amikor 1960-ban R. C. BOSE, S. S. SHRIKHANDE és E. T. PARKER példákat adtak 4n+2-rendű ortogonális latin négyzetekre, a történetileg is érdekes 10-edrendűt IV. táblázatunkban mutatjuk be:
 

0417298365815273940698263745105983047621769841503267098521433071986254123456078923456018974560123978         0786935412617809452350278196349613782045390247815684913572607859246301456012378912345609782345601897

 

IV.táblázat

 

A vizsgálatokból az is kiderül, hogy maximálisan n-1 n-edrendű, páronként ortogonális latin négyzet létezhet, és a latin négyzeteknek egy ilyen "teljes rendszere'' kombinatorikai szempontból igen jelentős; nyílt kérdés azonban, hogy milyen n-ekre szerkeszthetők meg ezek.
J. STEINER svájci matematikus 1853-ban vetette fel a következő kérdést: lehet-e egy n-elemű halmazban olyan ‐ blokkoknak nevezett ‐ háromelemű részhalmazokat képezni, hogy a halmaz bármely két eleme pontosan egy blokkhoz tartozzék hozzá. A feladat feltételét kielégítő halmazokat Steiner-rendszereknek nevezik. Már STEINER is tudta, hogy a halmaz elemszáma csak 6N+1 vagy 6N+3 lehet (N pozitív egész); néhány évvel később M. REISS megmutatta, hogy az ilyen elemszámú halmazokban valóban szerkeszthető Steiner-rendszer. Példaként megadjuk az n=6⋅1+1=7 elemű halmazban képezett Steiner-rendszert; ennek 7 blokkja van.
P1P2P3P4P5P6P7e1111e2111e3111e4111e5111e6111e7111

 

V. táblázat

A rendszer ábrázolására táblázatot használunk. Egy 7×7-es táblázat oszlopainak a halmaz elemeit, a sorainak a halmaz blokkjait feleltetjük meg; egy sor és oszlop közös mezőjére akkor és csakis akkor írunk 1-est, ha a sornak megfelelő blokk tartalmazza az oszlopnak megfelelő elemet (V. táblázat).
A Steiner-rendszer természetes általánosításaként vetődik fel a kérdés, hogy lehet-e az elemhármasok helyett elem k-asokat szerepeltetni a megadott feltételek mellett. Ilyen esetekben Steiner féle k-rendszerről beszélünk; a Steiner-féle k-rendszer tehát egy n elemű halmaz, amelyben blokkoknak nevezett k-elemű részhalmazok vannak úgy, hogy a halmaz bármely két eleme pontosan egy blokkban van egyszerre benne. Az ilyen rendszereknek a létezése már sokkal súlyosabb kérdés; a teljes válasz nem ismeretes.
A XIX. század végére jutott a geometria abba a helyzetbe, hogy mintegy két évezreddel EUKLIDÉSZ után modern igényű axiomatikus megalapozását elvégezzék. Ezzel egy időben került sor a geometria egy sajátos ágának, a projektív geometriának a megalapozására is.
A projektív síkgeometria "alapötlete'' annak a kivételes helyzetnek a megszüntetése volt, amit az euklidészi síkgeometriában a párhuzamosak léte okoz. Ezt azzal lehet elérni, hogy a párhuzamos egyenesnyalábokhoz egy "képzeletbeli'' pontot rendelünk hozzá, amit ideális pontnak mondunk, ezt a nyaláb minden egyenese tartalmazza. (Az ideális pont helyett használják a nem túl szerencsés végtelen távoli pont elnevezést is). A sík ideális pontjainak a halmazát ideális egyenesnek (végtelen távoli egyenesnek) nevezzük. A projektív sík az ideális elemekkel bővített euklidészi sík, legalábbis eredetileg ezt tekintették annak. A projektív sík szerkezetére jellemző, hogy bármely két egyenesének van közös pontja és bármely két pontjának van pontosan egy összekötő egyenese.
Ebből a klasszikus projektív síkfogalomból vonatkoztatták el a projektív sík ma használatos fogalmát, amely az alábbi axiómarendszerrel jellemezhető:
A projektív sík a pontoknak nevezett elemeknek nem üres halmaza; ennek bizonyos részhalmazait egyeneseknek nevezzük. Ha egy egyenes tartalmaz egy pontot, akkor azt mondjuk, hogy a pont rajta van az egyenesen, vagy a pont illeszkedik az egyeneshez. A projektív síkon teljesülnek a következő axiómák:
A1: Két ponthoz egy és csakis egy olyan egyenes van, amely mindkettőt tartalmazza.
A2: Két egyeneshez egy és csakis egy olyan pont van, amelyet mind a kettő tartalmaz.
A3: A síkon van legalább két egyenes. Minden egyenesnek van legalább három pontja.
A projektív síknak ez a definíciója igen általános, hiszen teljesen nyitva hagyja azt a kérdést, hogy mi lehet pont. Ezért erre a kérdésre csak ezt válaszolhatjuk: pont (és egyenes) lehet minden olyan "valami'', ami kielégíti az A1‐A3 axiómákat.
Álljon pl. a projektív sík egy osztály 31 tanulójából, ők a pontok. Tegyük fel, hogy az osztályban sikerül 31 egyesületet szervezni úgy, hogy minden egyesületnek 6 tagja van és bármely két tanuló pontosan egy egyesületnek tagja egyidejűleg, teljesül továbbá, hogy bármely két egyesület esetén pontosan egy olyan tanuló található, aki mindkét egyesületnek tagja. Ha egyeneseknek az egyesületeket tekintjük, az osztály projektív sík, hiszen kielégíti az axiómákat.
Azok a pontoknak, ill. egyeneseknek nevezett halmazok, amelyek kielégítik az A1‐A3 axiómákat, az axiómarendszer egy modelljét alkotják. A projektív sík egy modellje tehát az ideális elemekkel bővített euklideszi sík, de modellje az előbbi példa osztálya is.
Axiómarendszerünk igen gyengének tűnik, amiből igen kevés tétel vezethető le. Ez nagyjából így is van, de a múlt század végén G. FANO olasz matematikusnak és társainak a vizsgálataiból kitűnt, hogy lényegesen többet mondhatunk a síkról, ha axiómáinkhoz még egy végességi axiómát hozzáfűzünk:
A4: Van olyan egyenes, amelynek q+1 pontja van (q≧2).
Az A1‐A4 axiómákkal jellemzett halmaz a véges projektív sík; q a projektív sík rendje. Nézzük most meg vázlatosan, milyen tételek vezethetők le az A1‐A4 axiómákból.
1. Minden egyenesnek q+1 pontja van. Legyen ui. e1 az A4 szerint q+1 pontot tartalmazó egyenes és legyen e2 a sík egy tetszőleges egyenese, ezeknek A2 szerint van egy M közös pontja (1. ábra).
 
 
1. ábra
 

Legyenek e1 pontjai M, P1, P2, ..., Pq. Az e2-n A3 szerint van egy R1, R2 pontpár. A P1R1 és P2R2 egyenesek közös pontja legyen S. Az S-et a P3, P4, ..., Pq pontokkal összekötő egyenesek e2-t rendre az R3, R4, ..., Rq pontokban metszik. Az S-ből való vetítés tehát kölcsönösen egyértelmű megfeleltetést létesít e1 és e2 pontjai között, tehát  e2-nek, és így a sík bármely egyenesének is q+1 pontja van.
2. Minden pont q+1 egyenesen van rajta. Legyen K tetszőleges pont és e egy a K-t nem tartalmazó egyenes (A3-ból következik, hogy ilyen van). K-t összekötve e pontjaival q+1 különböző egyenest kapunk és több nem is lehet, mert A2 szerint ez is metszené e-t, ami lehetetlen, hiszen ekkor két pontot két egyenes is összekötne. K ezért q+1 egyenesen van rajta.
3. A síkon n=q2+q+1 pont van. Előző tételünkben a K-n átmenő (összes) q+1 egyenes a sík minden pontját tartalmazza, mert ha lenne még ezeken kívül pont, akkor K-t ezzel összekötve egy q+2-ik egyenest kapnánk, ami lehetetlen. A K-t tartalmazó egyenesek mindegyikén K-n kívül még q pont van, ezért a sík ponjainak a száma q(q+1)+1=q2+q+1.
4. A síkon q2+q+1 egyenes van. Válasszuk ki ui. a sík egy e egyenesét. Mivel ezt a sík minden egyenese metszi, elég az e-t metsző egyeneseket összeszámolni. e-t minden pontjában q egyenes metszi, ezért a sík egyeneseinek a száma n=q(q+1)+1=q2+q+1.
A q értéke tehát nagymértékben megszabja a sík szerkezetét. A legegyszerűbb véges projektív sík rendje 2. Ez a sík valóban létezik is; pontjainak és egyeneseinek a száma 22+2+1=7, minden egyenesen tehát 3 pont van. Ez a struktúra lényegében azonos az V. táblázattal adott Steiner-rendszerrel. Ez a táblázat felfogható a 2-rendű véges projektív sík illeszkedési táblázatának, ahol az oszlopokhoz a sík pontjait, a sorokhoz pedig a sík egyeneseit rendeljük hozzá; egy oszlop és egy sor közös mezőjébe akkor és csakis akkor írunk 1-est, ha a neki megfelelő pont, ill. egyenes illeszkednek egymáshoz. A táblázatból könnyen ellenőrizhető, hogy az így adott sík kielégíti az A1‐A4 axiómákat.
Ha ennek a véges síknak a pontjait és egyeneseit (hagyományos) pontokkal, ill. egyenesekkel akarnánk ábrázolni, nem sikerülne; legalább egy egyenest csak görbült vonallal tudunk megrajzolni. Maga a 7 pont alkotta alakzat minden projektív síkon fontos szerepet játszik. Szerkezetének a lényege a következő : négy pont, P2,P3,P4,P5 ún. teljes négyszöget alkot, közülük egyik három sincs egy egyenesen. A pontokat páronként összekötő 6 egyenes a teljes négyszög oldalai, ezeknek a csúcsokon kívüli metszéspontjai: P1,P7,P6 a négyszög átlóspontjai. Az átlóspontok a közönséges síkon nincsenek egy egyenesen, de ez nem következménye axiómarendszerünknek. Ha a teljes négyszög átlóspontjai egy egyenesen vannak, akkor Fano-négyszög a neve. A 2-rendű véges projektív sík azonos egy Fano-négyszöggel (2. ábra).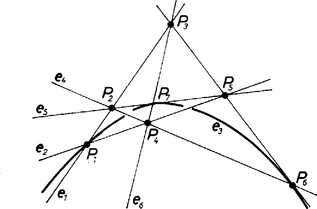
 
 
2. ábra
 

Az ortogonális latin négyzetek és a véges síkok kapcsolatát a harmadrendű síkon mutatjuk be. Itt q=3, a pontok és egyenesek száma 32+3+1=13. A sík szerkezetét a 3. ábrán vázoljuk.
 
 
3. ábra
 

Kiválasztjuk a síknak egy v egyenesét. Ennek pontjai E,G,A,B, az ezekből induló egyenesek (v-n kívül) rendre: e0,e1,e2; g0,g1,g2; a0,a1,a2; b0,b1,b2. Ábránkon a v egyenest nem rajzoltuk meg, a pontjain átmenő egyeneseket párhuzamos egyeneshármasokként indítottuk el. Az ei,gk egyenesek (i,k=0,1,2) metszéspontja legyen (i,k); ez a 9 pont a v pontjaival együtt kimeríti a sík pontjait. A (0,0),(1,0),(2,0) pontokat (ebben a sorrendben) az A-val, ill. a B-vel összekötő egyenesek: a0,a1,a2; b0,b1,b2. Írjuk fel, hogy ezek (ebben a sorrendben) mely pontokban metszik a g0,g1,g2 egyeneseket:
 

a0:(0,0)(1,1)(2,2)a1:(1,0)(2,1)(0,2)a2:(2,0)(0,1)(1,2)b0:(0,0)(2,1)(1,2)b1:(1,0)(0,1)(2,2)b2:(2,0)(1,1)(0,2)

 
Figyeljük meg, hogy az első koordináták mindkét egyenesnyalábnál szükségképpen latin négyzetet alkotnak (ez a két latin négyzet azonos az I, ill. II. táblázat latin négyzeteivel. A két latin négyzet ortogonalitása az axiómákból és abból a tényből következik, hogy a g0 egyenesen kívül két azonos számozású egyenes nem metszheti egymást.
Ha a v egyenesen még több pont lenne, azaz q nagyobb lenne 3-nál, akkor a pontjaiból induló egyenesek q-1 egyenesnyalábot állítanának elő, és hasonló módon q-1 latin négyzet keletkeznék, amelyek páronként ortogonálisak. Ezek szerint minden q-adrendű síkhoz tartozik a q-adrendű latin négyzeteknek egy teljes rendszere és megfordítva: egy ilyen teljes rendszer mindig létrehoz egy q-adrendű véges projektív síkot. A 36 tiszt problémájának a megoldhatatlanságából következik, hogy 6-odrendű véges sík nem létezik, de ha megoldható lenne, még nem következnék belőle a megfelelő véges sík létezése, mivel ahhoz q-1 páronként ortogonális latin négyzet szükséges. A IV. táblázattal megadtunk két 10-edrendű ortogonális latin négyzetet, de az igen nagyszámú vizsgálat ellenére sem tudjuk, hogy létezik-e 10-edrendű véges projektív sík.
Térjünk most már rá arra a kérdésre, hogy milyen q érték lehet a véges projektív sík rendje. Ehhez ismertetjük a sík legtöbbet alkalmazott szerkesztési módszerét. A szerkesztés módja algebrai, kiindulásunk egy igen érdekes algebrai struktúra, a véges test. A véges testben két műveletet: összeadást és szorzást értelmezünk, ezek kommutatívak és asszociatívak, mindkét műveletnek van inverze (kivonás, ill. 0 kivételével osztás), érvényes a disztributív szabály, tehát az összeget tagonként kell szorozni. A legegyszerűbb véges testek a prímszám modulusú maradékosztályok. A véges testek létezésének az alaptétele azt mondja ki, hogy ha p tetszőleges prímszám és α pozitív egész, akkor létezik egyetlen olyan véges test, amelynek elemszáma pα. Megfordítva: minden véges test elemszáma prímszámhatvány.
A véges testek felhasználásával projektív sík a következő módon szerkeszthető: legyen K tetszőleges véges test, elemszáma pα. Pontnak, ill. egyenesnek nevezzük a test elemeiből készített (x1,x2,x3), ill. (u1,u2,u3) elemhármasokat (bennük nem lehet minden elem 0). Két elemhármas ugyanazt a pontot, ill. egyenest jelenti, ha egyik a másikból egy testelemmel való végigszorzással származtatható. Az (x1,x2,x3) pont és az (u1,u2,u3) egyenes akkor és csakis akkor illeszkedik egymáshoz, ha u1x1+u2x2+u3x3=0. Bebizonyítható, hogy az így értelmezett pontok és egyenesek kielégítik az A1‐A4 axiómarendszert, és az egy egyenesen levő pontok száma pα+1, tehát a sík rendje q=pα.
Minden prímszámhatvány lehet tehát véges sík rendje. A fenti előállítású síkokon kívül még másféle síkok is léteznek, tehát olyanok, amelyek nem véges testre építettek; az eddig ismertek azonban mind úgy jönnek létre, hogy az előbbieket valamilyen módon átrendezzük, rendjük tehát ezeknek is prímszámhatvány. Rengeteg kutatás foglalkozott annak az eldöntésével, hogy prímhatványokon kívül lehet-e más szám a véges sík rendje, de a kutatások egyelőre nem vezettek eredményre, nem tudjuk pl. hogy létezik-e 10-edrendű véges projektív sík. Igaz, hogy végtelen sok számról tudjuk, hogy nem lehet a sík rendje; erre vonatkozó legtöbbet mondó eredmény R. H. BRUCK és H. J. RYSER amerikai matematikusoktól származik (1949): ha q=4k+1 vagy q=4k+2 és q prímtényezős felbontásában van páratlan kitevős 4N+3 alakú prím, akkor q nem lehet véges projektív sík rendje. Ezek szerint pl. q=6 nem lehet a sík rendje, de ez a tétel nem ad felvilágosítást a q=10 esetről.
A fentiek alapján alakult ki és tartja magát a következő, ún. pontszámsejtés:
 

A véges projektív sík rendje csak prímszámhatvány lehet.
 

Az eddig ismert, nem testre épített véges síkok teljes négyszögeit vizsgálva arra az eredményre jutottak, hogy mindegyik tartalmaz Fano-féle négyszöget, de ugyanakkor van olyan négyszöge is, amely nem Fano-féle. Egy testre épített síkon vagy minden teljes négyszög Fano-féle, vagy egy sem. A. M. GLEASON bebizonyította, hogy ha a síkon minden négyszög Fano-féle, akkor szükségképpen testre épített. Ezekből alakult ki a sejtés:
 

Ha a véges projektív síkon nincs Fano-féle négyszög, akkor az testre épített és így rendje prímszámhatvány.
 

A véges projektív síkok felfedezése sok ismeretet nyújtott a Steiner-féle k-rendszerekről is, hiszen minden véges projektív sík egyben Steiner-féle k-rendszer is, ahol k=q+1; a véges síkok azonban nem merítik ki az összes ilyen rendszert.
A pontszámsejtés megfelelőjét a latin négyzetek körében így fogalmazhatjuk meg:
 

A q-adrendű latin négyzetek teljes rendszere akkor és csakis akkor létezik, ha q prímszámhatvány.
 

A pontszámsejtés, ill. következményei kihatnak a kombinatorika számos kérdéskörére. Ebből most egyet említünk meg.
TURÁN PÁL 1941-ben egy gráfelméleti cikkével érdekes problémakör vizsgálatát indította el; az alapkérdés teljes általánosságában így hangzik: adott egy k csúcspontú G gráf és egy élnélküli n csúcsú gráf (n≧k). Az utóbbiba elkezdünk éleket berajzolni, ez 12n(n-1) él berajzolásával nyilván véget ér, ekkorra már minden lehetséges élt berajzoltunk a gráfba; ez az n csúcsú teljes gráf már biztosan tartalmaz G típusú (pontosabban: G-vel izomorf) részgráfot. Kérdés: maximálisan hány élt rajzolhatunk be a gráfba, hogy az még ne tartalmazzon G típusú részgráfot?
A probléma egy speciális esete a következő: Legyen Gn,n egy 2n csúcsú páros gráf, amelynek mindkét csúcshalmazában n csúcs van. (Egy gráf páros, ha csúcsai két, közös elem nélküli részre oszthatók úgy, hogy az azonos részekbe tartozó csúcsokat ne kösse össze él.) Maximálisan hány él rajzolható be a gráfba úgy, hogy a gráf ne tartalmazzon négyszöget? (A négyszög négycsúcsú gráf, két-két csúcsa különböző csúcshalmazban van, és minden lehetséges éllel össze vannak kötve. 4. ábra.)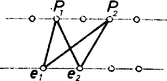
 
 
4. ábra
 

Kombinatorikai meggondolásokkal bebizonyítható, hogy ha Gn,n éleinek a száma nagyobb, mint

s(n)=12(n+n4n-3),




akkor már biztosan tartalmaz négyszöget; ez azonban nem zárja ki annak a lehetőségét, hogy már s(n) él mellett is van a gráfban négyszög. Ha bizonyos n-ekre meg tudjuk mutatni, hogy a gráf még s(n) élt tartalmazva is négyszögmentes lehet, akkor ezekben az esetekben s(n) adja meg a keresett maximális élszámot.
Érdekes módon, éppen a véges projektív síkok segítségével tudunk olyan Gn,n gráfokat szerkeszteni, amelyek négyszögmentesek, de s(n) élt tartalmaznak, méghozzá abban az esetben, ha n egy sík pontjainak a száma, tehát n=q2+q+1. Rendeljük ugyanis hozzá egy q-adrendű véges sík pontjaihoz, ill. egyeneseihez a Gn,n gráf egyik, ill. másik csúcshalmazát. Két csúcsot akkor kötünk össze éllel, ha a nekik megfelelő pont, ill. egyenes illeszkednek egymáshoz. Az így kapott gráf négyszögmentes, mert ha lenne benne négyszög (mint a 4. ábrán), akkor a sík P1 és P2 pontjait az e1 és e2 egyenesek is összekötnék.
Mivel minden pontra q+1 egyenes illeszkedik a síkon, a gráf minden olyan csúcsából, amely síkbeli pontnak felel meg, q+1 él indul, és így a gráf éleinek a száma n(q+1). Viszont az n=q2+q+1 egyenletből q-t, ill. q+1-et kifejezve kapjuk, hogy n(q+1)=s(n). Pl. a 2-rendű síkot felhasználva kapjuk, hogy n=7-re s(7)=21 a maximális élszám.
Bebizonyítható, hogy Gn,n négyszögmentesen csak akkor tartalmazhat s(n) számú élt, ha n véges projektív sík pontszáma. A pontszámsejtés megfelelője tehát a most vizsgált feladatnál a következő:
Egy négyszögmentes Gn,n gráf csak akkor tartalmazhat s(n) számú élt, ha n=p2α+pα+1 (p prím, α pozitív egész).