|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megjegyzések a 2778. feladathoz
Többen észrevették, hogy az F. 2778 feladat ,,folytatása'' az F. 2641. és F. 2661. feladatoknak. Az F. 2641. feladat azt állította, hogy akárhogyan adunk meg a zárt intervallumon véges sok pontot, mindig található hozzájuk olyan pont az intervallumban, amelynek tőlük vett átlagtávolsága , és ugyanez az állítás az szám helyett más számra nem teljesül.
Megismételjük a bizonyítást, mert a későbbiek legtöbb ötlete már ennek az egyszerű feladatnak a bizonyításánál is előkerül. Először is azt kell észrevennünk, hogy ha két pontot adunk meg, és ez a két pont az intervallum két végpontja, akkor egy tetszőleges pontnak tőlük vett átlagtávolsága mindig . A feladat állítása tehát valóban csak az számra teljesülhet. Másrészt legyen adva az intervallumon pont, , , , . Az pont tőlük vett átlagtávolságára teljesül, hogy , s ez folytonos függvény (-ban). Másrészt tetszőleges pontoknak a -tól és az -től vett távolságának összege , ezért . Így vagy , s ekkor a pontnak az pontoktól vett átlagtávolsága , vagy , de ekkor , s mivel folytonos, valahol és között van olyan , amelyre . A harmadik esetben, amikor is , ugyanez igaz. Mindenképp találtunk tehát egy pontot, amelynek az , , , pontoktól vett átlagtávolsága . Ezzel a tétel bizonyítását befejeztük.
Nyilvánvaló, hogy a fenti bizonyítás tetszőleges folytonos görbére elmondható, ha két pont ,,távolságán'' a két pont közötti görbeív hosszát értjük. Ehhez viszont szükséges, hogy a görbe véges hosszúságú legyen, ami nem minden folytonos görbére teljesül: a híres hópehelygörbe olyan folytonos görbe, amelynek tetszőleges két pontja között ,,végtelen hosszú'' az ív. A következő állítást kapjuk tehát:
Ha két (különböző) végpontú, véges hosszúságú folytonos görbe, amely nem metszi önmagát, akkor bármely véges sok pontjához található olyan pont a görbén, amelynek tőlük vett ,,távolság''-átlaga , és a szám mással nem helyettesíthető. A görbe két pontjának ,,távolságán'' a két pont közötti ív hosszát értjük.
Mielőtt továbbmennénk, bevezetünk egy új kifejezést. Tegyük fel, hogy az ponthalmazon értelmezve van egy ,,távolság'' (ez lehet az ívtávolság is, a szokásos sík-, ill. térbeli távolság is). Azt mondjuk, hogy e ,,távolság'' mellett varázsszáma -nek, ha az ponthalmaz bármely , , , pontjához van olyan pont -ben, amelynek az , , pontoktól vett átlag-,,távolsága'' . Előző tételünk most így fogalmazható:
1. tétel. Egy két végpontú, véges hosszúságú, önmagát nem metsző folytonos görbe egyetlen varázsszáma: .
Az F. 2778. feladat után írt megjegyzésben (374. old.) azt is megmutattuk, hogy igaz az alábbi
2. tétel. Egy önmagába záruló, véges hosszúságú, önmagát nem metsző folytonos görbe egyetlen varázsszáma .
Mindkét esetben az ívhosszt, illetve a rövidebbik ívhosszt értjük távolságon.
E két tételt először, úgy tűnik, P. Nicholas vette észre.
Az alábbi cikkben O. Gross, Joan Cleary, David Yost, A. Morris és P. Nicholas nyomán e tételeket messzemenően általánosítani fogjuk. Szükségünk lesz néhány definícióra és megjegyzésre.
A) Ha , , , a sík (a tér) pontjai és az pontnak tőlük vett átlagtávolsága (egyelőre a szokásos távolságot használjuk),akkor folytonos függvénye -nak. Ez azt jelenti, hogy minden számhoz van olyan , hogy ha , akkor . Ez egyszerűen következik a háromszögegyenlőtlenségből: így | |
(Két pont egymástól vett távolsága nem nagyobb adott ponttól vett átlagtávolságuk különbségénél.) Így választással éppen a kívánt állítást kapjuk.
Az ponthalmaz korlátos, ha van olyan kör a síkban, ill. gömb a térben, amely őt tartalmazza. Ekkor bármely két pontjának távolsága legföljebb akkora, mint a kör, ill. gömb átmérője. átmérője az a legkisebb szám, amelyre igaz, hogy semelyik két pontjának távolsága nem nagyobb -nél. Az ponthalmaz zárt, ha minden torlódási pontját tartalmazza. (Az ponthalmaznak a pont akkor torlódási pontja, ha hozzá tetszőlegesen közel van -nek -től különböző pontja.) Ismert tény, hogy korlátos ponthalmaz bármely végtelen , , , , pontsorozatának van torlódási pontja. Ha a ponthalmaz zárt, akkor e torlódási pontot tartalmazza is. Ebből adódik következő megjegyzésünk:
B) Ha korlátos, zárt ponthalmaz, akkor bármely végtelen , , , , pontsorozatának van -ben torlódási pontja.
Ebből viszont következik a harmadik megjegyzésünk:
C) Ha az korlátos, zárt halmaz átmérője , akkor van olyan és pont -ben, amelyek távolsága éppen . (Ha nem ad félreértésre okot, az ilyen szakaszt is átmérőjének fogjuk nevezni.)
Minden -re van ugyanis olyan és -ben, amelyre . Ekkor azonban a , , , , sorozat bármely és a , , , , sorozat bármely torlódási pontjára (a távolság folytonossága miatt) . Mivel zárt, is, is benne van, s mivel átmérője , ezért . Így , amit bizonyítani akartunk.
Most rátérünk tulajdonképpeni témánkra. Első új tételünk már nagyon általános ugyan, de még a ,,metrikus'' (távolsággal összefüggő) tulajdonságokon túl más geometriai tulajdonságokat is figyelembe vesz:
3. tétel. Ha az középpontosan szimmetrikus, korlátos, zárt, konvex (sík- vagy térbeli) tartomány átmérője , akkor egyetlen varázsszáma van, .
(Megjegyezzük, hogy az I. tétel levezethető ebből a tételből, ha a görbe helyett olyan ,,szakaszt'' tekintünk, ahol ,,nem egyenletes a távolság''.)
A 3. tételből következik jó néhány egyszerű sík-, ill. térbeli alakzat varázsszáma:
B. 1. következmények: A szokásos sík-, ill. térbeli távolság mellett
‐ az sugarú körlemez egyetlen varázsszáma , az ellipszistartományé a fél nagytengely;
‐ az egységoldalú négyzetlap egyetlen varázsszáma , az és oldalú téglalapé ;
‐ a (tömör) egységkocka egyetlen varázsszáma , az , , élű tömör tégláé .
‐ a szabályos -szögtartomány egyetlen varázsszáma a legnagyobb átló fele.
A 3. tétel nem ad felvilágosítást a szabályos -szögről, így a szabályos háromszögről sem.
Tételünk bizonyításához szükségünk van néhány egyszerű megjegyzésre:
D) Korlátos zárt halmaznak nincs az átmérő felénél kisebb varázsszáma.
Ha ugyanis a halmaz átmérője, akkor tetszőleges pontnak e két ponttól vett átlagtávolsága a háromszögegyenlőtlenség szerint. E két ponttól vett átlagtávolság tehát nem kisebb az átmérő felénél.
E) Ha egy halmaz belefoglalható egy sugarú körbe (ill. gömbbe), és tartalmazza annak középpontját, akkor nincs -nél nagyobb varázsszáma.
Ha ugyanis e kör, ill. gömb közepe, akkor tetszőleges pontnak -tól vett ,,átlagtávolsága'', azaz távolsága legföljebb .
A D) és E) megjegyzések alapján
F) ha egy korlátos és zárt halmaz átmérője , és belefoglalható egy sugarú körbe (ill. gömbbe), tartalmazza ennek a középpontját, akkor csakis lehet a varázsszáma.
F)-ből még nem következik, hogy valóban varázsszáma a halmaznak.
Térjünk most vissza a 3. tétel bizonyítására. Legyen középpontosan szimmetrikus, korlátos és zárt halmaz és legyen a középpontja. Legyen átmérője , és rajzoljunk köré sugarú kört, ill. gömböt. Ez a kör (ill. gömb) az egész halmazt tartalmazza. Ha ugyanis valamely pontja ,,kilógna'', arra teljesülne. De -nek -ra vonatkozó tükörképe is -hez tartozik, másrészt volna, ami ellentmondás. Ha tehát középpontosan szimmetrikus, korlátos és zárt, akkor teljesül rá az F) megjegyzés feltétele, így csakis lehet a varázsszáma.
Azt kell még belátnunk, hogy valóban varázsszáma -nek. Mivel belefoglalható egy középpontú, sugarú körbe, ill. gömbbe, így minden átmérője átmérője ennek a körnek (ill. gömbnek) is. Ha tehát az halmaz egy átmérője, akkor felezőpontja a -nak. Legyenek most , , , az halmaz pontjai, és egy átmérő. minden pontra, így -nek a -ktől vett átlagtávolsága és -nak a -ktől vett átlagtávolsága összesen legalább : | |
Ebből viszont következik, hogy és egyikének, pl. -nek a -ktől vett átlagtávolsága legalább . Az is világos, hogy , tehát -nak a -ktől vett átlagtávolsága legföljebb . Ha végigfut az szakaszon, akkor -nak a -ktől vett átlagtávolsága az A) megjegyzés szerint folytonosan változik. Valahol és között tehát van olyan pont, amelyre felveszi a értéket.
A bizonyítás ezzel ‐ majdnem ‐ kész is van. Azt kell még belátnunk, hogy valóban -ben van. Azt tudjuk, hogy a pont -ben van, és is. Eddig nem használtuk, hogy az halmaz konvex. Ezt felhasználva viszont kapjuk, hogy a szakasz minden pontja -ben van, és rajta van ezen a szakaszon. Ezzel a 3. tétel bizonyítását befejeztük.
Említettük már, hogy a 3. tétel nem elég a szabályos -szögtartomány varázsszámának megállapításához. Az általános háromszöglap varázsszámához sem elég. Most egy általánosabb, Szekeres Györgytől és Szekeres Esztertől származó tételt fogunk bebizonyítani, ami legalábbis a szabályos -szöglap és a nem-hegyesszögű háromszöglap esetére jó:
4. tétel. Ha korlátos, zárt, síkbeli konvex halmaz, és a legkisebb, -et lefedő kör sugara , akkor varázsszáma -nek.
E tételből már egyszerűen adódik az alábbi:
4.1. következmények: A derékszögű háromszöglap egyetlen varázsszáma az átfogó fele.
A tompaszögű háromszöglap egyetlen varázsszáma a leghosszabb oldal fele.
Ha ugyanis a háromszög nem hegyesszögű, akkor a leghosszabb oldala mint átmérő fölé írt kör lefedi az egész háromszöget, s ez nyilván az egész háromszöget lefedő legkisebb kör. Másrészt a háromszög átmérője a legnagyobb oldala, így az F) megjegyzés szerint csakis a leghosszabb oldal fele lehet varázsszám, s a 4. tétel szerint ez valóban varázsszáma a nem-hegyesszögű háromszögnek.
Hegyesszögű háromszögre ugyanez a bizonyítás kevesebbet ad:
4.2. következmény: A hegyesszögű háromszögnek a köré írt kör sugara varázsszáma, és nincs -nél nagyobb varázsszáma.
Az E) szerint ugyanis nincs -nél nagyobb varázsszáma, és a 4. tétel alapján valóban varázsszáma, hiszen a hegyesszögű háromszöget lefedő körök közül a köré írt kör a legkisebb.
4.3. következmény: A szabályos háromszög egyetlen varázsszáma a köré írt kör sugara.
A köré írt kör a legkisebb a szabályos sokszöget lefedő körök közt, tehát a 4. tétel szerint ennek sugara valóban varázsszám. Az E) megjegyzés szerint nincsen -nél nagyobb varázsszáma. Végül, ha a sokszög csúcsait választjuk pontoknak, akkor egy tetszőleges pontnak tőlük vett távolságösszege ‐ s így átlagtávolsága is ‐ a szabályos sokszög középpontjában minimális az ismert tétel szerint; így tetszőleges pontnak a csúcsoktól vett átlagtávolsága legalább . Nincs tehát -nél kisebb varázsszám sem.
Most rátérünk a 4. tétel bizonyítására:
Legyen a legkisebb, -et tartalmazó kör közepe. (Hogy ilyen van, azt ahhoz hasonlóan lehet belátni, ahogyan C)-t bizonyítottuk.)
Tegyük fel, hogy , , , az halmaz pontjai, és legyen a súlypontjuk. Tekintsük a legkisebb, középpontú kört, amely az egész halmazt lefedi. Ilyen nyilván van, és a sugara legalább . Az halmaz zártsága miatt található a körön -beli pont (ez megint C)-hez hasonlóan bizonyítható); legyen egy ilyen pont . Ekkor és | |
tehát a pontnak a pontoktól vett átlagtávolsága legalább . Másrészt az pontnak a pontoktól vett átlagtávolsága legfeljebb , hiszen minden -re. Minthogy az átlagtávolság folytonos (lásd az A) megjegyzést), ezért van olyan pont az szakaszon, amelynek a pontoktól vett átlagtávolsága éppen .
A bizonyítással ismét csak majdnem vagyunk készen. Be kell még látnunk, hogy az halmazban van. A pontról ezt tudjuk, így konvexitása miatt elég megmutatni, hogy is -ben van. Ez azonban most korántsem olyan magától értetődő. (Láttuk pl., hogy a tompaszögű háromszög esetében a háromszög határán van.) A következő segédtételt fogjuk e célból bizonyítani:
G) Ha konvex, zárt, korlátos tartomány a síkban, akkor az -et lefedő legkisebb kör középpontja -ben van.
 1. ábra
Legyen a legkisebb lefedő kör, és legyen a középpontja; legyen továbbá a kör egy tetszőleges átmérője. Ha -n nincs pontja -nek, akkor a konvexitása miatt teljes egészében a egyenes egyik oldalán van. zárt, így minden támaszegyenesén van pontja. A ezek szerint nem támaszegyenes. Húzzuk meg a -vel párhuzamos, -höz közelebbi támaszegyenest. Ez és pontokban metszi a kört (1. ábra). Ekkor az egész benne van abban a tartományban, amelyet az szakasz és a rövidebbik körív határol. Ennek a tartománynak az átmérője , és az mint átmérő fölé rajzolt kör teljesen lefedi. Így nem a legkisebb az -et lefedő körök közül, hiszen . Ez az ellentmondás bizonyítja, hogy a kör minden átmérőjén van pontja -nek. Ha az az és szakaszon is van pontja, akkor tartalmazza ezek összekötő szakaszát (hiszen konvex), így az pontot is.
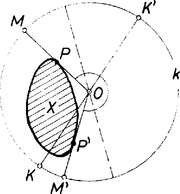 2. ábra
Tegyük fel tehát, hogy pl. -n nincs pontja -nek. Forgassuk el az sugarat körül pozitív és negatív irányban addig, amíg nem kerül rá -nek egy-egy pontja. zártsága miatt van egy első olyan helyzete a sugárnak, amikor tartalmazza valamely pontját. Legyen ez a helyzet pozitív irányban az , negatív irányban az sugár (2. ábra). egy -hez tartozó pontja legyen , egy -hez tartozó pontja legyen . Ha a -t tartalmazó , akkor metszené -t. De a konvexitás miatt minden pontja -ben van, így -nek is lenne közös pontja -szel. Ha , akkor az szög szögfelezőjére -ban húzott merőleges olyan átmérőegyenese volna a körnek, amely egyetlen pontját sem tartalmazná (mivel az egész a konvex szögtartomány belsejében van). Ez viszont, mint láttuk, lehetetlen. Így marad az az eset, ha . Ekkor a szakasz tartalmazza -t, a szakaszt pedig tartalmazza . Ezzel állításunkat beláttuk.
Itt jegyezzük meg, hogy még nehezebb a fenti állítás térbeli megfelelőjét bizonyítani, ami viszont szükséges a következő ‐ egyébként a 3. tétellel teljesen megegyezően igazolható tételhez:
3. tétel: Ha korlátos, zárt és konvex térbeli ponthalmaz, és a legkisebb, -et lefedő gömb sugara, akkor varázsszáma -nek.
Térjünk most vissza az F. 2661. feladathoz, ami a következő ‐ J. Clearytől származó ‐ tétel bizonyítását követelte (ahol már nem konvex):
4. tétel: Az a oldalú szabályos háromszög kerületének varázsszáma , ha a pontok távolságain a rendes síkbeli távolságot értjük.
Ennek bizonyításához legyen a szabályos háromszög három csúcsa a három kiválasztott pont, és legyen pl. a oldal egy tetszőleges pontja (3. ábra). Ekkor és , a háromszög magassága. Így az pontnak , , pontoktól vett átlagtávolsága legalább .
 3. ábra
Ennél kisebb varázsszám tehát nincsen. Legyen másrészt , , rendre a , , oldal felezőpontja, és legyen pl. a szakasz pontja. Ekkor , így , másrészt (ha létrejön), így a háromszögben (ha létrejön) . Ha a háromszög nem jön létre (azaz ), akkor . Mindenképpen azt kapjuk, hogy , s így -nak az , , pontoktól vett átlagtávolsága legfeljebb
Végül legyenek , , , a kerület tetszőleges pontjai. Az , és pontoknak -től vett távolságösszege ‐ mint láttuk ‐ legfeljebb , így az , az és az pontoknak a -ktől vett távolságainak összege is legföljebb ennyi:
Ebből következik, hogy valamelyik -nek, pl. -nek a -ktől vett átlagtávolsága legföljebb . Ugyanígy látható be, hogy , , valamelyikének a , , -től vett átlagtávolsága legalább . Ha az pont végigfut a kerületen -től ezen pontig (ezt kétféle úton is teheti), akkor a -ktől vett átlagtávolsága az A) megjegyzés szerint folytonosan változik, így valahol pontosan lesz az átlagtávolság.
A tétel állításánál ‐ csakúgy, mint a hozzá nagyon hasonló 2. tétel esetén ‐ kicsit többet bizonyítottunk: az egyetlen varázsszám a , és minden , , , ponthalmazhoz legalább két olyan pont van, amelynek tőlük vett átlagtávolsága .
Most gondoljuk végig, mi kellett a 4. tétel bizonyításához. Az halmaz továbbra is korlátos és zárt volt, de most a konvexitás nem teljesült. Fontos volt viszont, hogy bármely két pontja között vezetett folytonos út -ben. Az ilyen halmazokat összefüggőnek nevezzük. D. Gross még 1964-ben valóban bebizonyította, hogy ,,ennél több nem is kell''.
5. tétel. Ha korlátos, zárt és összefüggő ponthalmaz, akkor pontosan egy varázsszáma van.
A tétel két dolgot állít. Egyrészt azt állítja, hogy -nek van varázsszáma, másrészt azt, hogy csak egy varázsszáma van. Ez utóbbi bizonyításához nagyon erős mértékelméleti segédeszközök kellenek, elemi bizonyítás nem ismert rá. Így az 5. tételnek csak egy részét fogjuk igazolni, hogy -nek a fenti feltételek mellett van varázsszáma. Már ebből is több szép eredmény következik. Először ezeket mutatjuk meg. (az itt következő 6. és 7. tétel is J. Clearytől való).
6. tétel. Az egységoldalú négyzet kerületének varázsszáma , ha két pont távolságán a szokásos síkbeli távolságot értjük.
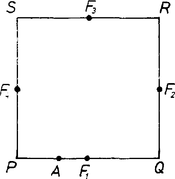 4. ábra
Mivel tudjuk, hogy van varázsszám (hiszen korlátos, zárt és összefüggő), elég azt belátni, hogy sem -nél nagyobb, sem annál kisebb nem lehet. Legyen a négyzet, és válasszuk ki mindjárt a négy csúcsát. Legyen a kerület egy tetszőleges pontja . Feltehető, hogy pl. a oldalon van. Ekkor . Másrészt a oldal felezőpontjára minimális (4. ábra), ezért . Így átlag távolsága a csúcsoktól legalább , tehát a varázsszám sem lehet ennél kisebb. Legyen most , , , rendre a , , , oldalnak a felezőpontja, és legyen pl. a szakasz pontja. Ekkor , így Másrészt az háromszögben (ha létrejön) , így , s ugyanígy . (Ha , akkor mindkét helyen egyenlőség áll.) Így az pontnak az oldalfelezőpontoktól vett átlagtávolsága legfeljebb , tehát a varázsszám sem lehet ennél nagyobb.
Ezzel beláttuk, hogy a varázsszám csak lehet.
Megjegyezzük, hogy ez a bizonyítás is befejezhető lett volna ugyanúgy, mint a szabályos háromszög esetében, nem kellett volna az 5. tételre hivatkozni.
A 4. és 6. tétellel teljesen analóg módon számítható ki minden szabályos sokszög kerületének a varázsszáma: | |
ha a szabályos -szögről van szó, és a köré írt kör sugara .
Végül ugyancsak J. Cleary bizonyította a következő, valamivel már trükkösebb tételt is:
7. tétel. Az , oldalú téglalap kerületének (a síkon mért távolság mellett) az egyetlen varázsszáma , ha .
8. tétel. A körvonal varázsszáma (a síkon mért távolsággal) , ahol a kör átmérője.
A 7. tétel bizonyítását az Olvasóra hagyjuk. Megjegyezzük viszont, hogy a sokszögek, sőt még a konvex sokszögek kerületére sem ismert olyan általános tétel, mint amilyet a konvex sokszögtartományokra ad a 4. tétel.
A 8. tételt S. A. Morris és P. Nickolas bizonyította. Ők számították ki a gömb felszínének a varázsszámát is, ez ‐ átmérő esetén ‐ . Az -dimenziós gömb felszínének varázsszámát is meghatározták. Ez , , , -re rendre (lásd a 8. tételt), , , . Mi most az esetet, tehát a 8. tétel bizonyítását mutatjuk be. Felhasználjuk az 5. tételnek itt bizonyításra nem kerülő részét is, mert ez lényegesen egyszerűsíti dolgunkat: azt kell csak belátnunk, hogy varázsszám. Nyilván feltehető, hogy . Rögzítsünk az egységsugarú, középpontú kör kerületén egy ,,kezdőpontot'', és egy irányítást a körön. Legyenek továbbá a körön a , , , pontok és egy pont. Az távolság nyilván , ahol az (irányított) körív hossza, vagyis a irányított szög radiánokban mért nagyságának abszolút értéke. Ha tehát , (irányított szögek, , , akkor , (5. ábra).
 5. ábra
Így az pontnak a pontoktól vett átlagtávolsága: . Fusson most végig a kör kerületén úgy, hogy -tól -ig változik. Az integrálközép tétele szerint lesz olyan helyzete, ahol
Az összegben minden integrál egyenlő, hiszen mindegyiknél az távolságot kell ,,körbeintegrálnunk'' a körön egy fix pontra, és nyilván mindegy, hogy ez a pont hol helyezkedik el. Ezért mindegyik integrál értéke annyi, mint ha a pontban volna, azaz volna, tehát | |
Azt kaptuk, hogy (1) jobb oldala tehát van olyan pont a körön, amelyre .
Megjegyezzük, hogy itt is ,,meg lehetne úszni'' az 5. tétel ,,keményebb'' felére való hivatkozást. Ha ugyanis a , , , pontokat egy szabályos -szög csúcsainak választjuk a körön, akkor egy tetszőleges kerületi pontnak a -ktől vett átlagtávolsága már ( növekedésével) tetszőlegesen közel kerül a értékhez. Ennek végiggondolását az Olvasóra bízzuk.
Mielőtt az 5. tétel első felét bizonyítanánk, térjünk vissza a 4. tételhez és következményeihez. A háromszögtartományok közül csak a nem-hegyesszögűeket tudtuk teljesen elintézni. A hegyesszögű háromszögekről csak annyit láttunk be, hogy a köré írt kör sugara varázsszám, és nagyobb nincs. Az 5. tétel ,,erősebbik'' része szerint azonban pontosan egy varázsszám van. Általában is igaz a következő:
4 tétel. Ha korlátos, zárt, konvex sík- vagy térbeli halmaz és az -et lefedő legkisebb kör (ill. gömb) sugara , akkor egyetlen varázsszáma .
4.2 következmény. A hegyesszögű háromszög egyetlen varázsszáma a köré írható kör sugara.
E két állításra is adhatnánk elemi bizonyítást; javasoljuk az Olvasónak, hogy próbálkozzon meg vele! Hiszen ,,most már nem sok'' hiányzik hozzá.
Befejezésül a 4. tételnek még egy érdekes következményét említjük meg. Ha tetszőleges, síkbeli, korlátos, zárt és összefüggő halmaz, akkor varázsszáma az E) és G) megjegyzés alapján legföljebb , hiszen belefoglalható egy tetszőleges pontja körüli sugarú körbe, másrészt legalább a D) megjegyzés szerint. Az belátható, hogy pontosan sem lehet, tehát a [, ) balról zárt, jobbról nyitott intervallumba esik. Általában ennél többet azonban nem tudunk mondani. Ha viszont csak konvex halmazokra szorítkozunk, akkor a felső korlát lényegesen lejjebb szorítható:
9. tétel. Ha konvex, síkbeli, zárt, átmérőjű tartomány, akkor varázsszáma és közé esik. Így egyetlen ilyen halmaz varázsszáma sem nagyobb, a oldalú (átmérőjű) szabályos háromszögénél.
A 4. tétel szerint ehhez elég belátni, hogy bármely átmérőjű konvex alakzat belefoglalható egy sugarú körbe, s ez éppen Jung tétele. (A Jung-tétel bizonyítása pedig azon az egyszerű tényen alapszik, hogy ha az háromszög oldalai legföljebb hosszúságúak, akkor a háromszög belefoglalható egy legfeljebb sugarú körbe. Valóban: ha a háromszög hegyesszögű, akkor köré írt köre legfeljebb sugarú, ha nem hegyesszögű, akkor sugarú körbe is belefoglalható. Ezek után tekintsük az halmaz minden pontja körül a sugarú kört és jelöljük -val. Ha , , az halmaz három pontja, akkor a , , köröknek van közös pontja: az háromszöget lefedő sugarú kör közepe. Helly tétele szerint ekkor az összes körnek van közös pontja, s az e pont körüli sugarú kör nyilván tartalmazza az összes pontot, tehát az egész -et.)
Most befejezésül bebizonyítjuk az 5. tételnek azt a részét, hogy minden korlátos, zárt és összefüggő ponthalmaznak van varázsszáma.
Legyenek , , , az halmaz pontjai. Az pontnak a tőlük vett átlagtávolságára teljesül, hogy , ahol az halmaz átmérője. (Ez abból látszik, hogy minden -re.) Ebből az A) megjegyzés alapján már következik, hogy folytonos, korlátos függvény. Megmutatjuk, hogy -nek van maximuma -ben. Legyen az függvény értékkészletének legkisebb felső korlátja . Minden pozitív egész számra van olyan pontja -nek, amelyre . Mivel korlátos halmaz, az , , , , pontsorozatnak van torlódási pontja; legyen ilyen torlódási pont. Az pont -ben van, mert zárt. Válasszuk ki az , , , , pontsorozatnak egy -hoz tartó , , , , részsorozatát. Ekkor folytonossága miatt . Másrészt , tehát , így az pontnak a pontoktól vett átlagtávolsága , azaz -ban -nek maximuma van. Ugyanígy bizonyítható az is, hogy van olyan pont -ben, ahol felveszi a minimumát. Végül összefüggő, ezért és között fut folytonos görbe -ben, s ezen folytonosan változik, tehát ezen az minden értéket felvesz a minimuma és a maximuma között. Ezzel beláttuk, hogy tetszőleges , , , pontok esetén az átlagtávolság-függvény értékkészlete egy zárt (korlátos) intervallum, jelöljük ezt -vel, ahol .
Az állítás, amit bizonyítani akartunk, azt állítja, hogy van egy olyan szám, amely minden ilyen intervallumban benne van, akárhogyan választjuk is a , , , pontokat. Ehhez viszont elég belátni, hogy ha és két tetszőleges ponthalmaz -ben, akkor , azaz a , , , pontoktól vett átlagtávolság minimuma nem nagyobb a , , , pontoktól vett átlagtávolság maximumánál. Tekintsük az összes szakaszok hosszának összegét és osszuk el a számukkal, -mel. Így megkapjuk a , , , pontoknak a pontoktól vett átlagtávolságainak az átlagát, s ez nyilván nem nagyobb a pontoktól vett átlagtávolság maximumánál, -nél. Másrészt ugyanennyi a , , , pontoknak a pontoktól vett átlagtávolságainak az átlaga is, az meg nyilván nem kisebb a pontoktól vett átlagtávolság minimumánál, -nél. Ezzel viszont beláttuk, hogy a kapott szám -nél nem kisebb, -nél nem nagyobb, ami csak úgy lehet, ha . Ezzel az 5. tétel bizonyítását befejeztük.
Megjegyezzük, hogy a bizonyítás semmi mást nem használ -ről, mint hogy bármely két pontja között definiálva van egy nem-negatív távolság, ami csak akkor nulla, ha a két pont azonos, és hogy igaz rá a háromszög-egyenlőtlenség: , ahol az és pont távolságát jelöli. Ha pontjai között definiálva van egy ilyen ,,távolság''-metrika, akkor -et metrikus térnek nevezzük. korlátos, ha belefoglalható egy pontja körüli, elég nagy sugarú gömbbe, ahol az közepű, sugarú gömb azokból az pontokból áll, amelyekre (azaz amelyek -től legföljebb távolságra vannak). Ekkor az A) megjegyzés érvényben marad, így -ről a korlátosság mellett azt kell még megkövetelni, hogy minden végtelen pontsorozatának legyen -ben torlódási pontja, és legyen összefüggő. Ha e három kikötés teljesül az metrikus térre, akkor igaz rá az 5. tétel: pontosan egy varázsszáma van. O. Gross eredetileg ezt bizonyította. Az itt közölt bizonyítás szó szerint átvihető a varázsszám létezésének bizonyítására ilyen metrikus térben.
Befejezésül néhány feladat:
1. feladat. Tekintsük az egységsugarú körvonalat és egy átmérőjét. Mi ennek az alakzatnak a varázsszáma?
2. feladat. Legyen az hegyesszögű háromszög , , csúcsánál a szög rendre , , . Igazoljuk, hogy a összeg a sík összes pontja közül a körülírt kör közepére minimális.
3. feladat. Igazoljuk a 2. feladat segítségével a 4.2 következmény ,,hiányzó'' részét, vagyis azt, hogy a háromszög varázsszáma nem lehet a köré írt kör sugaránál kisebb.
4. feladat. Igazoljuk, hogy ha egy zárt, korlátos, konvex tartományt lefedő legkisebb kör sugara nagyobb a tartomány átmérőjének felénél, akkor e kör kerületének legalább 3 közös pontja van a tartománnyal.
5. feladat. A 2. és 4. feladat felhasználásával igazoljuk a 4-tétel még ,,hiányzó'' részét, tehát azt, hogy egy korlátos, zárt, konvex tartomány varázsszáma nem lehet kisebb a tartományt lefedő legkisebb kör sugaránál.
Helly tétele azt mondja ki, hogy ha korlátos és zárt, konvex síkbeli halmazok közül bármely háromnak van közös pontja, akkor az összesnek is van. A körök megfelelnek ennek a feltételeknek. |
 PDF | MathML
PDF | MathML