|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A sokszögek átdarabolásának vizsgálata egy sor érdekes kérdést vet fel, az alábbi cikkben ezek közül mutatunk be néhányat. Az átdarabolás itt azt jelenti; az egyik sokszöget véges sok részre osztjuk, melyek maguk is sokszögek, majd ezek egybevágó példányaiból összeállítjuk a másikat. Egyszerű átdarabolási feladatokkal valószínűleg mindenki találkozott az általános iskolában, hiszen az alapvető területszámítási képleteket így szokás bizonyítani.
1. Bolyai és Gerwien tétele
Az első tétel arra az általános esetre vonatkozik, amikor semmilyen megszorítás nincsen azokra a részekre, amelyekre az egyik alakzatot felvágjuk, sem pedig azokra az egybevágósági transzformációkra, amelyek az első alakzat részeit a második alakzat megfelelő részeibe viszik. A tételt Bolyai Farkas fedezte föl ‐ és tőle függetlenül mások is ‐ és azt mondja ki, hogy:
Bármely két egyenlő területű sokszög átdarabolható egymásba.
A feltétel nyilván szükséges. A tétel állítása egyáltalán nem nyilvánvaló, de hogy miért nem az, az még sokkal kevésbé nyilvánvaló: tudniillik nem igaz a térbeli megfelelője.
A tételt több lépésben bizonyítjuk. Első lépésben megmutatjuk, hogy minden háromszög átdarabolható egy téglalapba.
A bizonyítás leolvasható az 1. ábráról. Ügyelnünk csak arra kell, hogy a magasság a háromszög belsejében haladjon, ami viszont teljesül, ha a legnagyobb oldalhoz tartozó magasságot rajzoljuk meg.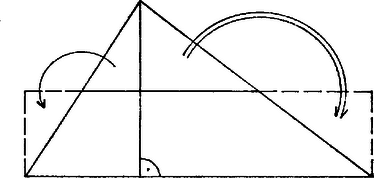
 1. ábra
Érdemes felfigyelni arra, hogy az eljárás során csak kétfajta mozgatást használtunk: a trapézt helyben hagytuk, a két háromszöget pedig elforgattuk 180-kal.
A második lépés annak bizonyítása, hogy két azonos területű téglalap ugyancsak átdarabolható egymásba, méghozzá szerencsés esetben 3 rész felhasználásával.
Legyen tehát az és a oldalú téglalapok területe egyenlő, helyezzük el őket a 2. ábrán látható módon, és vágjuk szét a szaggatott "átló'' mentén. Az feltétel nyilvánvaló következményeként ‐ gondolja meg az Olvasó ‐ mind a satírozott , mind pedig a derékszögű háromszögek egybevágóak. (Utóbbiak közös része az ötszöget téglalappá kiegészítő kis derékszögű háromszög.)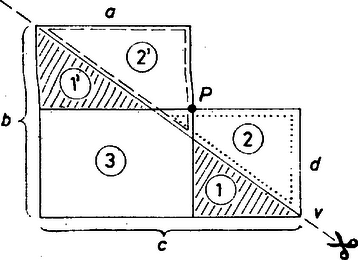
 2. ábra
Vegyük észre, hogy most csak az eltolást és helybenhagyást használtuk, a részek száma pedig ismét három volt. A fenti eljárás azonban csak akkor alkalmazható, ha az oldalaknak az ábrán vel jelölt metszéspontja a egyenes felett van. Ez sajnos nem teljesül, ha valamelyik téglalap túl keskeny. Ezen azonban könnyű segíteni. Gondolja meg az Olvasó, hogy a 2. ábra elrendezése mindig megkapható, ha a két téglalap oldalainak aránya 1 és 2 közé esik. Ezt úgy biztosíthatjuk, ha a szereplő téglalapokat előbb átdaraboljuk a 3. ábrán látható lépést megfelelően sokszor elvégezve.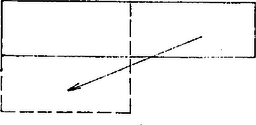
 3. ábra
Ez azt jelenti, hogy az egyenlő területű és téglalapoknak a 2. ábrán bemutatott átdarabolását az általános esetben csak e téglalapoknak a 3. ábra eljárásával kapott és átdarabolt példányaival tudjuk elvégezni, más szóval egyelőre a átdarabolások sorozatán keresztül vezet az út ből be. Az, hogy a átdarabolás közvetlenül is megvalósítható, most már abból következik, hogy a síkidomok között az átdarabolhatóság tranzitív reláció, tehát ha síkidomokra és , akkor is teljesül. Az állítás meglehetősen nyilvánvaló: ha a mind az , mind pedig a síkidomba átdarabolható, akkor mindkét felosztását elvégezve olyan kisebb részeket kapunk, amelyekből mind az -t, mind pedig a -t alkotó részek összerakhatók, azaz ezek alkalmas összerakásával -ból közvetlenül kaphatjuk -t. Megjegyezzük, hogy ez az okoskodás felhasználta azt a nyilvánvaló tényt is, hogy az átdarabolhatóság szimmetrikus, tehát ha , akkor is fennáll.
Összefoglalva azt kapjuk, hogy alakzatok között az átdarabolhatóság ekvivalencia-reláció.
A bizonyításra visszatérve vegyük észre még, hogy a 2. és 3. ábrákon bemutatott elemi átdarabolási lépések során az egyes részeket kizárólag eltolások felhasználásával mozgattuk, így végül azt bizonyítottuk be, hogy két egyenlő területű "egyállású'' téglalap eltolások segítségével egymásba darabolható. A fenti állításból az "egyállású'' feltétel kiküszöbölhető, ha meggondoljuk, hogy bármely téglalap átdarabolható adott állású téglalappá, mégpedig szintén csak eltolások segítségével. Két egymásra merőleges egyenessel kijelölve az elérendő oldalirányokat, téglalapunkat először olyan paralelogrammává darabolhatjuk át, amelynek egyik oldala párhuzamos a tengelyek egyikével, ezután pedig a másik oldalt is "kiegyenesíthetjük'' (4. ábra).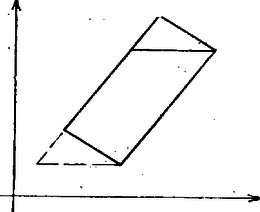
 4/a. ábra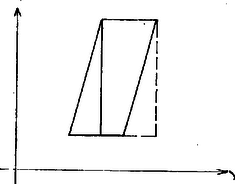
 4/b. ábra
Ehhez persze szükséges, hogy legyen olyan kiszemelt tengelyiránnyal párhuzamos egyenes, amelyik a paralelogramma két szemközti oldalának egy-egy pontját köti össze. Ha ilyen nincsen, azaz a paralelogramma szemközti oldalait a másik tengelyre vetítve nincs a vetületeknek közös pontja, akkor ezen pl. a 3. ábra eljárásával segíthetünk.
Összefoglalva tulajdonképpen azt láttuk be, hogy bármely paralelogramma átdarabolható olyan paralelogrammába, melynek oldalai egy-egy megadott iránnyal párhuzamosak.
A Bolyai‐Gerwien tétel bizonyításának befejező lépéseként azt igazoljuk, hogy tetszőleges sokszög átdarabolható adott állású téglalapba.
Bontsuk fel ehhez a sokszöget háromszögekre ‐ ez a lépés egyáltalán nem magától értetődő, de szemléletesen annyira nyilvánvaló, hogy most itt elfogadjuk ‐, a háromszögeket az első lépés szerint daraboljuk át téglalappá, majd ezeket az "összevissza'' álló téglalapokat daraboljuk át egyállású téglalapokká. Ezeket az egyállású téglalapokat pedig daraboljuk át olyan téglalapokká, melyek egyik ‐ vízszintes ‐ oldala adott, például egységnyi hosszúságú. Az így kapott téglalapokat egységnyi oldaluk mentén egymáshoz fűzve olyan téglalapot kapunk, melynek vízszintes oldala egységnyi, területe pedig egyenlő a kiindulásul vett sokszögével. Ha tehát az és az sokszögek területe egyenlő, akkor mindketten éppen a kapott téglalapba darabolhatók, és így a tranzitivitás miatt egymásba is átdarabolhatók.
Ez a Bolyai ‐ Gerwien tételnek egy lehetséges bizonyítása. Az eljárás igen gazdaságos, ami a használt mozgásokat illeti. Ha végiggondoljuk, akkor egyetlen lépéstől eltekintve kizárólag eltolások juttatják új helyükre a részeket. Kivétel az a lépés, amikor egy háromszöget téglalappá alakítunk át: a kis háromszögek ekkor -os forgatással kerülnek a helyükre. Ez az észrevétel fölveti a kérdést: lehetséges-e egy háromszöget csupán eltolások segítségével téglalappá alakítani? Ebből ugyanis a bizonyítás gondolatmenete szerint már az is következne, hogy két egyenlő területű sokszög eltolásokkal is egymásba darabolható.
2. Egymásba tolható sokszögek, egy érdekes invariáns
Feladatunk tehát a következő: adott egy háromszög és egy vele egyenlő területű téglalap. Felosztható-e a háromszög olyan részekre, amelyeket alkalmasan eltolva megkapjuk a téglalapot?
Némi próbálgatás után reménytelennek tűnik a dolog, és a válasz valóban tagadó, de ennek bizonyítása ‐ mint az ilyen típusú lehetetlenségi bizonyításoké általában ‐ nem is olyan egyszerű. Egy tipikus kiút, ha sikerül olyan mennyiséget találnunk ‐ úgynevezett invariánst ‐ amelyik nem változik a megengedett lépések során, értéke azonban nem egyenlő a kezdeti és a cél állapotban. Nagyon egyszerűen működik ez az elv például akkor, ha azt akarjuk bizonyítani, hogy ha két sokszög területe különböző, akkor a sokszögek nem darabolhatók egymásba. Érdemes azonban szemügyre venni ennek az egymondatos bizonyításnak a részleteit.
Az első tény, hogy minden sokszögnek van területe, egy pozitív valós szám. A második, hogy az átdarabolás során ez a szám nem változik, invariáns. Miért? Mert az átdarabolás során használt két lépés, a sokszög részekre osztása, illetve a részek elmozgatása nem változtatja meg a részek területének összegét, illetve maguknak a részeknek a területét, és így, mivel egy sokszög részei területének összege a sokszög területével egyenlő, az átdarabolás után kapott sokszög területe egyenlő kell legyen a kiindulási sokszög területével.
Ha sikerülne olyan függvényt találnunk, amelyik ugyanígy viselkedik, tehát | a) | minden sokszöghöz hozzárendel egy valós számot; |
| b) | ha a sokszöget részekre ‐ sokszögekre ‐ osztjuk, akkor a részekhez rendelt számok összege a sokszöghöz rendelt szám; |
| c) | egy sokszög bármely eltolt példányához ugyanazt a számot rendeli, mint a sokszöghöz; |
végül ‐ és főleg ‐ az értéke különböző egy háromszögre, illetve egy vele egyenlő területű téglalapra, akkor készen volnánk a bizonyítással.
Ilyen függvényt a következőképpen találunk:
Jelöljünk ki egy irányt, majd haladjunk végig pozitív körüljárás szerint az kerületén. Utunk során kizárólag a megadott iránnyal párhuzamos oldalak hosszát vegyük figyelembe, összegezzük őket, mégpedig pozitív előjellel, ha a megadott iránnyal egyezőek, negatív előjellel, ha azzal ellentétesen jártuk be a szóban forgó oldalt. Az így kapott valós számot ‐ ami negatív is lehet, ellentétben a területtel, illetve nulla, ha például a sokszögnek nincsen a megadott iránnyal párhuzamos oldala ‐ rendeljük az sokszöghöz.
Gondoljuk meg, hogy az így kapott függvény valóban rendelkezik a b) és c) tulajdonságokkal, tehát additív és invariáns. Az utóbbi nyilvánvaló, hiszen az eltolás sem az oldalak irányát, sem pedig a hosszukat nem változtatja meg. (Ugyanez természetesen nem áll az elforgatásra, különböző irányokra általában különböző értékek adódnak.)
A b) tulajdonság bizonyításához vegyük észre, hogy az sokszög belsejében haladó oldalszakaszok két részsokszöget határolnak, amelyek kerületét pozitív körüljárás szerint bejárva ellenkező irányban megyünk végig a közös határszakaszon, így ezek járuléka a két részből összesen mindenképpen nulla, akár párhuzamos ez a szakasz a kiszemelt iránnyal, akár nem. Így a részekre kiszámolt függvényértékeket valójában elegendő az sokszög kerülete mentén figyelembe venni, s így a részekhez rendelt számok összegeként valóban az -hez rendelt értéket kapjuk. (A bizonyítás így még nem egészen pontos, meg kell mutatnunk, hogy a részsokszögeknek az -sel közös határszakaszain éppen jó irányban haladunk végig, de ennek igazolását az Olvasóra hagyjuk.)
A kiinduló kérdésre visszatérve ez azt jelenti, hogy ha két sokszög, és eltolások segítségével egymásba darabolható, akkor bármely irány mentén egyenlő kell hogy legyen a rájuk kiszámolt előjeles összeg. Mármost vegyük észre, hogy téglalapra ‐ és paralelogrammára ‐ ez a mennyiség minden irányra nulla. Ha nincs az adott iránnyal párhuzamos oldal, akkor azért, ha pedig van, akkor kettő ilyen van, és ezeken ellenkező irányban haladunk végig.
Ami viszont a háromszöget illeti, három olyan irány is van ‐ a háromszög oldalainak iránya ‐ amelyekre nullától különböző értéket kapunk. Ezzel a bizonyítást befejeztük, a háromszög és a téglalap valóban nem darabolhatók egymásba kizárólag eltolások segítségével.
Ha most általában vizsgáljuk a kérdést, akkor ahhoz, hogy két sokszög eltolások segítségével egymásba darabolható legyen, a területek egyenlőségén túl az is szükséges, hogy bármely irányra egyenlő legyen a két sokszögön kiszámolt előjeles összeg.
Háromszögekre nézve ez például azt jelenti, hogy két egyenlő területű háromszög csak abban a triviális esetben darabolható egymásba kizárólag eltolások segítségével, ha a két háromszög oldalai páronként egyállásúak és egyenlő hosszúak: az egyik háromszög teljes egészében eltolt példánya a másiknak.
Tekintsük most azt az esetet, amikor a "célsokszög'' négyzet ‐mint láttuk, ez lényegében egyenértékű a paralelogrammával ‐, azaz vizsgáljuk meg, mely sokszögek darabolhatók át négyzetbe kizárólag eltolások segítségével. Mivel négyzeten minden irányban nulla az adott irányú oldalak előjeles összege, ezért ennek az -re is teljesülnie kell. A talált feltétel viszont elegendő is, igaz az alábbi tétel.
Ha egy sokszög olyan, hogy bármely rögzített iránnyal párhuzamos oldalait körüljárás szerint előjelesen összegezve nullát kapunk, akkor eltolások segítségével négyzetbe darabolható.
Az állítás egyszerűen adódik olyan sokszögekre, amelyek oldalai között összesen kétféle irány van. Ilyen "paralelogrammaszerű'' sokszög látható az 5. ábrán.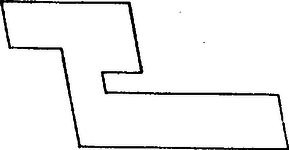
 5. ábra
Erre a sokszögre természetesen teljesül a tétel feltétele is, az adott irányú oldalak egy-egy nulla összegű vektorlánccá fűzhetők össze. Az egyik irányú oldalegyenesek paralelogrammákra osztják a sokszöget; ezeket eltolásokkal egységnyi vízszintes oldalú téglalapokká darabolhatjuk, amelyeket egymáshoz fűzve egyetlen téglalapot kapunk, ami eltolásokkal négyzetbe darabolható.
A továbbiakban teljes indukciót alkalmazunk az oldalirányok száma szerint. Legyen tehát az sokszögnek -féle oldaliránya . A bizonyítás során sokszögünkből levágunk egy téglalapba darabolható részt úgy, hogy a megmaradó sokszögnek eggyel kevesebb oldaliránya legyen és persze továbbra is teljesüljön rá a feltétel, tehát alkalmazni tudjuk majd rá az indukciós föltevést.
Válasszunk ki egyet az oldalirányok közül ‐ legyen ez a vízszintes irány ‐ és építsünk az ilyen irányú oldalakra a sokszög belsejében "fűrészfogakat'', melyek oldalai a sokszög további két kiszemelt oldalával párhuzamosak (6. ábra). Ez a két irány nyilván megválasztható úgy, hogy a fűrészfogakat a sokszög a belsejében tartalmazza, amennyiben azok elég kicsik, azaz a vízszintes oldalszakaszok végpontjából induló élek ne lépjenek ki a sokszögből.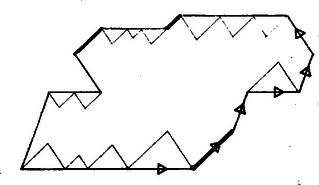
 6. ábra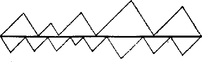
 7. ábra
Vegyük szemügyre először a levágott részt, a fűrészfogak egyesítését. Helyezzük őket egy szakaszra úgy, hogy a pozitív irányú oldalszakaszokon állókat felülre, a negatív irányú szakaszokon állókat pedig alulra rajzoljuk (7. ábra). Mivel a pozitív és a negatív irányú vízszintes oldalszakaszok hossza a feltétel szerint egyenlő, a levágott fűrészfogrendszer egy olyan zárt sokszögbe rendezhető eltolásokkal, melynek összesen két irányú oldala van, és így, mint láttuk, eltolásokkal négyzetbe darabolható.
Ami a megmaradó részt illeti, annak a vízszintes irányú oldalait megszüntettük, tehát oldalai -féle irányúak. A feltételt, hogy bármely irány mentén nulla az ilyen irányú oldalak előjeles összege, csak a fűrészfogak éleihez felhasznált két irányra kell ellenőrizni, hiszen az ezektől különböző irányú oldalak nem változtak. Itt csak arra van szükség, hogy a fűrészfogak járuléka nulla, ez pedig nyilvánvaló, hiszen a 7. ábra sokszögére, mint láttuk, ez teljesül. Ezzel megvan az indukciós lépés, és így a bizonyítás teljes.
Nyilvánvaló, hogy a fenti tétel feltétele teljesül, ha az sokszög centrálszimmetrikus. Meg lehet mutatni, hogy konvex sokszögek esetén ez a feltétel valójában ekvivalens azzal, hogy centrálszimmetrikus. Ennek az a következménye, hogy
egy konvex sokszög akkor és csak akkor darabolható négyzetbe eltolások segítségével, ha centrálszimmetrikus.
Hasonló ötlettel bizonyítható az általános tétel is, amely azt mondja ki, hogy
ha két sokszög területe egyenlő, továbbá minden irányra a sokszögeknek az adott irányhoz kiszámolt előjeles összegei megegyeznek, akkor a két sokszög átdarabolható egymásba eltolások segítségével.
3. Téglalapok felbontásai, additív függvények
Térjünk most vissza a téglalapokhoz. Láttuk, hogy ezek eltolásokkal is egymásba darabolhatók, ha egyenlő a területük. Korlátozzuk tovább a feladatot, tegyük fel, hogy a felbontásban szereplő részek is csak téglalapok lehetnek. Az első téglalapot tehát téglalapokra akarjuk bontani úgy, hogy ezekből eltolásokkal a másikat lehessen összeállítani. Feltesszük, hogy a két téglalap egyenlő területű, és hogy oldalaik párhuzamosak. A Bolyai‐Gerwien tétel bizonyításakor háromszögeket és ötszögeket is használtunk, így ha téglalapokból is megoldható az átdarabolás; akkor ezt más módszerrel kell megtalálnunk. Az is elképzelhető, hogy nem minden esetben oldható meg a feladat, ennek tisztázására ismét alkalmas additív és invariáns mérőszámot kellene találnunk. A téglalapokat persze a területen kívül az előjeles összeg sem különbözteti meg, hiszen az utóbbi a téglalapokon minden irányra nulla.
Az alábbiakban megadunk egy újabb, a kérdés tisztázására alkalmas mértéket. Ehhez ismét a terület viselkedéséből indulunk ki. Egy téglalap területe az oldalainak a szorzata. Az, hogy egy téglalapot két téglalapra osztva a részekre kiszámolt szorzatok összege a nagy téglalapra kiszámolt szorzattal egyenlő, a valós számok jól ismert disztributív tulajdonságán múlik: 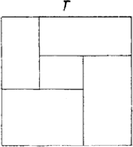Ezt átgondolva próbálkozhatunk további területjellegű függvények készítésével, amelyek additívak. Vehetjük például a két oldal valamilyen függvényének, az -nak és a -nek a szorzatát. Akármilyen függvények persze nem jók, most annak kell teljesülnie, hogy | |
azaz és ugyanígy, ha a másik oldal mentén vágjuk szét a téglalapot, akkor szükséges. Ha találtunk olyan és függvényeket, amelyek additívak a fenti értelemben, akkor az oldalú téglalap "területe'' is az lesz, mégpedig egyszerűen a disztributivitás miatt: bárhogyan osztunk egyállású téglalapokra egy téglalapot, a részek "területének'' összege a "területe'' lesz. Ehhez persze meg kell még vizsgálnunk az olyan típusú felosztásokat is, amikor nincs közös egyenlő oldalszakasza a téglalapoknak (8. ábra).
 8. ábra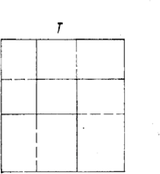
 9. ábra
Rajzoljuk meg ekkor a résztéglalapok oldalegyeneseit (9. ábra). Ezek már olyan "rácsszerű'' felbontását adják a téglalapnak, melynek részei a 8. ábra téglalapjait is élben egymáshoz csatlakozó téglalapok egyesítéseként állítják elő. Így a 8. ábra részeire kiszámolt "területek'' a 9. ábra. szerint olyan tagokra bonthatók tovább, melyek összege a "területével'' egyenlő.
Mármost van-e olyan függvény, amelyre teljesül, hogy minden valós , számra? Ilyen függvény persze van; ha , akkor ezek a lineáris függvények minden valós -re additívak, ez azonban a régi "területtel'' egyenértékű, lényegében új hosszúságegység választását jelenti, és így egyenlő területű téglalapokon egyenlő értékeket vesz föl. Van-e ezektől különböző típusú megoldása a () függvényegyenletnek?
Megmutatjuk, hogy van ilyen, sőt, ha egy adott irracionális szám, akkor -et úgy is megadhatjuk, hogy és teljesüljön.
Könnyen látható, hogy tetszőleges pozitív egész számra ()-ból következik; másfelől | |
Így az "majdnem lineáris'', legalábbis ami a racionális szorzókat illeti, azaz ha racionális, akkor Így ha -nek az 1 helyen fölvett értékét 1-nek választjuk, akkor()-ból tetszőleges racionális számra következik. Hogyan értelmezzük most az függvényt irracionális számokra?
Mivel értékét nullának akarjuk megválasztani, ez a döntésünk () és () alapján minden helyen meghatározza értékét, ahol és racionális számok: | |
Ehhez persze az is szükséges, hogy az alakba írható számoknak ez az alakja egyértelmű legyen, de ez nyilvánvalóan következik abból, hogy irracionális.
Mármost ha nem áll elő alakban, akkor természetesen irracionális, másfelől ‐ és ez a fontos ‐ eddigi értelmezése és a () feltétel semmilyen megszorítást nem jelent , illetve értékeire, így a () tulajdonság érvényben marad, ha -et is -nek definiáljuk.
A fenti eljárás a teljes valós számkörre kiterjeszthető: megmutatható, hogy bármely irracionális számból kiindulva létezik irracionális számoknak olyan halmaza ‐ ezek lesznek az függvény nulla helyei ‐ hogy , és minden irracionális szám egyértelműen áll elő alakban, ahol és racionális számok, és .
Ha most ennek a felbontásnak az alapján definíció szerint akkor ez az függvény additív lesz, és .
Legyenek most és olyan valós számok, amelyekre irracionális, és válasszuk a fenti halmaz elemének -t. Ekkor nyilván additív lesz az függvény is, ahol az előbbi, és erre az függvényre | |
Eredményeinket összefoglalva azt kaptuk, hogy ha irracionális szám, akkor létezik olyan additív függvény, hogy
Térjünk most vissza a téglalapokhoz. Legyenek a téglalapok oldalai és , illetve és . Mivel a területük egyenlő, , azaz . Ha most racionális, akkor persze is az, ami azt jelenti, hogy léteznek olyan és pozitív számok, hogy és egész számú többszöröse -nek, és pedig egész számú többszöröse -nek. Ekkor pedig mindkét téglalap felbontható ‐ mégpedig nyilván ugyanannyi ‐ méretű kis téglalapra, a két téglalap tehát felbontható téglalapokra úgy, hogy a részekből mindkét téglalap eltolásokkal megkapható. Az is látszik, hogy a felbontások a lehető legegyszerűbbek, a részek egybevágók.
Mi a helyzet akkor, ha irracionális? Megmutatjuk, hogy ekkor semmilyen felbontás nem alkalmas. Vezessünk be egy új területfüggvényt a talált additív függvénnyel, melyre tehát . Legyen egy oldalú téglalap "területe'' . Ekkor az így definiált terület is additív az egyállású téglalapokon, másrészt nyilván invariáns az eltolással szemben. Mivel pedig az első téglalap új "területe'' , a másodiké pedig , bebizonyítottuk, hogy
ha két téglalap egyállású oldalainak aránya irracionális, akkor bárhogyan osztjuk téglalapokra egyiküket, ezek eltolt példányaiból nem rakható ki a másik téglalap.
Másképpen fogalmazva: ha egyáltalán megoldható a feladat, akkor ez a 10. ábra triviális módszerével is lehetséges.
 10. ábra
 11. ábra
Felhívjuk a figyelmet, hogy itt lényeges az oldalak megkülönböztetése. A 11. ábra egybevágó téglalapjaira például nem oldható meg a feladat, hiszen forgatást nem engedünk meg.
Befejezésül az eddigiek következményeként egy önmagában is érdekes állítást bizonyítunk be.
Egy téglalap akkor és csak akkor bontható föl négyzetekre, ha oldalainak aránya racionális.
Az elégségesség nyilvánvaló, ekkor ugyanis a két oldal egy közös mértékét választva kapjuk, hogy rácsszerű felbontás is létezik.
Megfordítva tegyük föl, hogy az oldalú téglalap fölbontható négyzetekre (12. ábra).
 12. ábra
Forgassuk el a téglalapot kal! Az első felbontás négyzetei most eltolással vihetők a második téglalap négyzeteibe, így a téglalapokra kapott általános tétel szerint valóban racionális.
IRODALOM
[1] Reiman István: A geometria és határterületei, Gondolat, 1986, 299‐310. oldal.
[2] D. O. Skljarszkij‐N. N. Csencov‐I. M. Jaglom: Válogatott feladatok és tételek az elemi matematika köréből, Geometria II. (Sztereometria), Tankönyvkiadó, 1968, 81‐119. feladatok.
P. Gerwien német matematikus 1832ben, Bolyai Farkassal egy időben publikálta a tételt. A tétel első felfedezője W. Wallace angol matematikus volt; ő már 1807-ben közölte ezt az eredményt. |
PDF | MathML