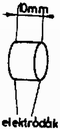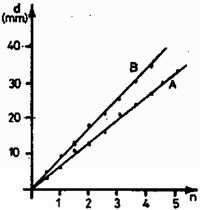Kezdőlap


Cím:	Az 1989. évi (20.) Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Gnädig Péter , Szép Jenő
Füzet:	1989/november, 401 - 407. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Tekintsünk két folyadékot, $A$ -t és $B$ -t, amelyek nem oldódnak egymásban. E folyadékok telített gőzeinek nyomása $p_{i}$ , ( $i = A$ vagy $B$ ) jó közelítésben a következő képletből számolható:

\begin{matrix} ln \frac{p_{i}}{p_{0}} = \frac{a_{i}}{T} + b_{i}, (i = A, B), \end{matrix}

ahol

p_{0}

a normál nyomást jelöli,

T

a gőz abszolút hőmérséklete, továbbá

a_{i}

és

b_{i}

, (

i = A

vagy

B

) a folyadékokra jellemző állandók (

ln

a természetes logaritmust jelöli, amelynek alapszáma

e = 2, 7183

p_{i} / p_{0}

arány értékei az

A

és a

B

folyadékokra,

40^{\circ} C

és

90^{\circ} C

hőmérsékleten az alábbi táblázatban vannak megadva:

\begin{matrix} t(^{\circ}C) & p_{i} / p_{0} \\ i = A & i = B \\ 40 & 0,284 & 0,07278 \\ 90 & 1,476 & 0,6918 \end{matrix}

Ezen értékek hibái elhanyagolhatóak.

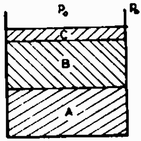1. ábra

a) Határozd meg az

A

és

B

folyadékok forrási hőmérsékleteit a

p_{0}

nyomáson!
b) Az

A

és

B

folyadékokat egy edénybe öntöttük, amelyben az

1.

ábra szerinti rétegek alakultak ki. Azért, hogy a szabad párolgást a

B

folyadék felszínéről megakadályozzuk, a

B

folyadék felületét egy nem párolgó

C

folyadékkal fedtük be, amely nem oldódik sem

A

, sem

B

folyadékokban, és azok sem oldódnak benne. Az

A

és

B

folyadékok molekuláinak tömegaránya (gáz állapotban):

\begin{matrix} γ = μ_{A} / μ_{B} = 8. \end{matrix}

A

és

B

folyadékok tömege kezdetben egyforma,

m = 100 g

. A rétegek vastagsága és a folyadékok sűrűsége olyan, hogy feltehetjük: az edényben a nyomás gyakorlatilag mindenhol megegyezik a külső légnyomással.
Ezekután lassan, folyamatosan és egyenletesen melegíteni kezdjük a folyadékrendszert.
Azt találjuk, hogy a folyadék

t

hőmérséklete a

τ

idő függvényében a

2.

ábrán vázolt módon változik.

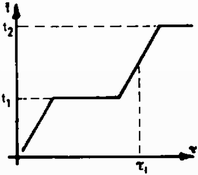2. ábra

Határozd meg az ábra vízszintes szakaszainak megfelelő

t_{1}

, és

t_{2}

hőmérsékleteket! Számítsd ki az

A

és a

B

folyadék tömegét az ábrán látható valamely

τ_{1}

időpillanatban! A

t_{1}

és

t_{2}

hőmérsékletet kerekítsd egész (Celsius) fokra, a folyadék tömegét pedig tizedgramm pontossággal add meg!

MEGJEGYZÉS: Feltesszük, hogy a vizsgált folyadékok gőzei jó közelítéssel
I) eleget tesznek a Dalton-törvénynek, azaz a gázok keverékeinek nyomása egyenlő a gázkeveréket alkotó gázok parciális nyomásainak összegével,
II) egészen a telített gőznek megfelelő nyomásig ideális gáznak tekinthetők.

Megoldás. 1.a) Először határozzuk meg az

a_{1}

és

b_{1}

állandókat! Helyettesítsük a táblázatban megadott számadatokat az

\begin{matrix} ln (p_{i} / p_{0}) = a_{i} / T + b_{i}, (i = A vagy B) \end{matrix}

egyenletbe! Ekkor mindkét folyadékra egy kétismeretlenes lineáris egyenletrendszert kapunk, amelynek megoldása:

\begin{matrix} a_{A} = - 3748, 5 K, b_{A} = 10, 711, a_{B} = - 5121, 6 K, b_{B} = 13, 735. \end{matrix}

Egy folyadék akkor forr, ha telített gőzének nyomása megegyezik a külső légnyomással. A feladat jelöléseivel ekkor

p_{i} / p_{0} = 1

, tehát

T_{f i} = - a_{i} / b_{i}

, ahol

T_{f}

a forrási hőmérsékletet jelöli. Adatainkkal

T_{f A} = 345 K = 77^{\circ} C

T_{f B} = 373 K = 100^{\circ} C

.
1.b) A hőmérséklet‐idő grafikon kezdeti szakasza arra utal, hogy az edényben a folyadék kezdetben párolgás nélkül melegszik, majd

t_{1}

hőmérsékleten forrni kezd. A forrás azt jelenti, hogy a folyadék belsejében telített gőzt tartalmazó buborék jön létre, amelyben a gáz nyomásának legalább akkorának kell lennie, mint a külső nyomás. Melyik az a legalacsonyabb hőmérséklet, amelyen ez létrejöhet? Az

A

és

B

folyadékok határfelületén keletkező buborékban mindkét folyadék telített gőze jelen lehet, és így a nyomás a két telített gőz nyomásának az összege. Ez a nyomás már az egyes folyadékok forrási hőmérsékleténél kisebb hőmérsékleten is eléri a külső légnyomást. A

t_{1}

hőmérsékleten tehát a

p_{A} + p_{B} = p_{0}

összefüggés teljesül. A feladatban megadott egyenletből a nyomást kifejezve és a fenti összefüggésbe írva az

\begin{matrix} e^{\frac{a_{A}}{T_{1}} + b_{A}} + e^{\frac{a_{B}}{T_{1}} + b_{B}} = 1 \end{matrix}

egyenletet kapjuk. Ezt legegyszerűbben a számadatok behelyettesítésével és

T_{1}

értékének többszöri változtatásával oldhatjuk meg. Az egész fokra kerekített eredmény

T_{1} = 340 K

, azaz

t_{1} = 67^{\circ} C

. A forrás az

A

és

B

folyadék határán tehát már ezen a hőmérsékleten megindul. Egy ilyen buborékban a telített gőzök nyomását ismét a feladatban megadott egyenlet segítségével számíthatjuk:

p_{A} = 0, 734 p_{0}, és p_{B} = 0, 267 p_{0}

. Most már meghatározhatjuk az egyes folyadékok gőzének tömegarányát a buborékban:

m_{A} / m_{B} = (p_{A} / p_{B}) \cdot (μ_{A} / μ_{B}) = 22, 0

. (Ez az arány a buborék felszállása során nem változik.) Tehát a határfelületi forrás során az

A

folyadék

22

-szer gyorsabban fogy. Ez a forrás addig tart, míg az

A

folyadék teljesen el nem fogy, és ekkor a

B

folyadékból még

100 g - (100 / 22) g = 95, 5 g

marad. Ennyi tehát a

B

folyadék tömege a

τ_{1}

pontban, amikor a forrás befejeztével a hőmérséklet ismét emelkedik. A forrás ezután már csak a

B

folyadék forráspontján indul el ismét, tehát

t_{2} = 100^{\circ} C

2. feladat. Három ‐ nem egy egyenesbe eső ‐ pontban (

P_{1}, P_{2}, P_{3}

-ban) adott

m_{1}

m_{2}

és

m_{3}

tömegű pontszerű testek találhatók, amelyek közti kölcsönhatás egyedül a gravitációs erőkből származik; más testekkel nem állnak kölcsönhatásban.
Jelöljük a három tömegpontból álló rendszer tömegközéppontján átmenő és a

P_{1} P_{2} P_{3}

háromszög síkjára merőleges tengelyt

σ

-val. Milyen feltételnek kell fennállni a

\bar{P_{1} P_{2}} = d_{12}

\bar{P_{2} P_{3}} = d_{23}

és

\bar{P_{1} P_{3}} = d_{13}

távolságok között, valamint

e

távolságok és a rendszer (

σ

tengelyre vonatkoztatott)

ω

szögsebessége között, hogy a

P_{1} P_{2} P_{3}

háromszög alakja a rendszer mozgása során változatlan maradjon, vagyis milyen feltételek teljesülése esetén forog a rendszer a

σ

tengely körül merev testként?

Megoldás. Jelöljük az egyes tömegpontok helyvektorát

r_{1}

r_{2}

és

r_{3}

-mal. Célszerű a koordinátarendszer origóját a tömegközéppontba választani, ekkor fennáll az

\begin{matrix} m_{1} \cdot r_{1} + m_{2} \cdot r_{2} + m_{3} \cdot r_{3} = 0 \end{matrix}

(1)

vektoregyenlőség.
Írjuk fel az

m_{1}

tömegű test mozgásegyenletét:

\begin{matrix} - m_{1} r_{1} \cdot ω^{2} = \frac{f \cdot m_{1} m_{2}}{d_{12}^{3}} (r_{2} - r_{1}) + \frac{f \cdot m_{1} m_{3}}{d_{13}^{2}} (r_{3} - r_{1}), \end{matrix}

(2)

ahol

f

a Newton-féle gravitációs állandó. Az (1) egyenletből

r_{3}

-at kifejezve és (2)-be helyettesítve az

\begin{matrix} r_{1} (\frac{ω^{2}}{f} - \frac{m_{1} + m_{3}}{d_{13}^{3}} - \frac{m_{2}}{d_{12}^{3}}) = r_{2} (\frac{1}{d_{13}^{3}} - \frac{1}{d_{12}^{3}}) \cdot m_{2} \end{matrix}

(3)

összefüggést kapjuk. Mivel

r_{1}

és

r_{2}

különböző irányú vektorok, (3) jobb és bal oldala csak úgy lehet mégis egyenlő, hogy a zárójelben lévő kifejezések nullák. Innen

\begin{matrix} d_{12} = d_{13} és ω^{2} \cdot d_{12}^{3} = f (m_{1} + m_{2} + m_{3}) \end{matrix}

adódik. A másik két test hasonló (az indexek felcserélésével adódó) mozgásegyenletét is felírva végül a keresett feltételek:

(I)

d_{12} = d_{23} = d_{13} = d

és

(II)

ω^{2} \cdot d^{3} = f \cdot M

,

ahol

M = m_{1} + m_{2} + m_{3}

, a rendszer össztömege.

3. feladat.Ebben a feladatban annak a lehetőségét és következményeit vizsgáljuk, hogy miként lehet egy elektronmikroszkópot (amely

U = 511 kV

potenciálkülönbséggel felgyorsított elektronnyaláb mágneses eltérítésével működik) protonmikroszkóppá alakítani, amelyben a protonnyalábot

- U

potenciálkülönbséggel gyorsítjuk fel.
Oldd meg az alábbi két részfeladatot:
a)Az elektron, miután

U

potenciálkülönbséggel felgyorsították, elhagyja a gyorsítót, és egy inhomogén

B

mágneses térbe jut. Ezt a mágneses mezőt a

T_{1}

T_{2}

...

T_{n}

jelzésű rögzített tekercsekből álló rendszer hozza létre. A tekercsekben

i_{1}

i_{2}

...

i_{n}

erősségű egyenáram folyik. A tekercsek által létrehozott erőtérben az elektronok egy bizonyos

P

pályagörbén mozognak.
Mekkora

i_{1}^{*}

i_{2}^{*}

...

i_{n}^{*}

erősségű áramoknak kell a

T_{1}

T_{2}

...

T_{n}

tekercseken folyni, hogy egy

- U

potenciálkülönbséggel felgyorsított proton ugyanazon a

P

pályagörbén (és ugyanabban az irányban) mozogjon a mágneses térben, mint az előbb az elektron?

ÚTMUTATÁS: A feladatot úgy oldhatod meg, hogy megkeresed azt a feltételt, amely mellett a

P

pályagörbét meghatározó egyenlet mindkét esetben ugyanaz. Felhasználhatod az alábbi összefüggést:

\begin{matrix} p \cdot \frac{d p}{d t} = \frac{1}{2} \cdot \frac{d (p^{2})}{d t} = \frac{1}{2} \cdot \frac{d p^{2}}{d t} . \end{matrix}

b) Hányszorosára nőne vagy csökkenne az adott mikroszkóp felbontóképessége, ha az elektronnyalábot protonnyalábbal helyettesítenénk? Feltételezzük, hogy a mikroszkóp felbontóképessége (vagyis az a legkisebb távolság két tárgypont között, amelyeknek kör alakú képei még elkülönülten láthatók) csak a részecskék hullámtulajdonságától függ.
Feltételezzük, hogy az elektronok, illetve a protonok sebessége a gyorsításuk előtt nulla. Az egyszerűség kedvéért feltesszük továbbá, hogy az elektronok és protonok saját mágneses momentumának a mágneses mezővel való kölcsönhatása elhanyagolható, és hogy a mozgó részecskék által kibocsátott elektromágneses sugárzás is elhanyagolható.

MEGJEGYZÉS: Fizikusok gyakran használják az energia egységeként az

1

elektronvoltot (

1

eV), és ennek többszöröseit, mint pl.

1

keV,

1

MeV.

1

elektronvolt energiára tesz szert az az elektron, amely 1 V potenciálkülönbségen halad át.
A számításnál használd fel a következő számadatokat:
az elektron nyugalmi energiája:

E_{e} = m_{e} c^{2} = 511 keV,

a proton nyugalmi energiája:

E_{p} = m_{p} c^{2} = 938 MeV .

Megoldás. a) Mivel a felgyorsított elektron mozgási energiája összemérhető (éppen egyenlő) a nyugalmi energiával, a relativisztikus

\begin{matrix} \frac{d p}{d t} = F_{L} . \end{matrix}

(1)

mozgásegyenletet kell alkalmaznunk. Ebben

\begin{matrix} p = \frac{m_{e}}{\sqrt[]{1 - v^{2} / c^{2}}} v \end{matrix}

(2)

m_{e}

nyugalmi tömegű,

v

sebességű elektron impulzusa,

\begin{matrix} F_{L} = e_{e} v \times B \end{matrix}

(3)

pedig az

e

töltésű elektronra ható Lorentz-erő. Mivel ez az erő merőleges a sebességre (és emiatt az impulzusra is), a megadott matematikai összefüggést felhasználva azt kapjuk, hogy

\begin{matrix} \frac{d p^{2}}{d t} = 2 \cdot p \frac{d p}{d t} \sim p \cdot F_{L} = 0. \end{matrix}

Az impulzus vektorának nagysága tehát a mágneses mezőben történő mozgás során állandó. Hasonlóan nem változik a sebesség nagysága sem, emiatt az (1) mozgásegyenlet az

\begin{matrix} \frac{m_{e}}{\sqrt[]{1 - v^{2} / c^{2}}} \cdot \frac{d v}{d t} = e_{e} v \times B \end{matrix}

(4)

alakot ölti. Mivel a pályagörbe bármelyik kicsiny darabja közelíthető egy

R

sugarú körívvel (

R

a görbületi sugár), s az egyenletes körmozgás gyorsulása

\begin{matrix} | \frac{d v}{d t} | = \frac{v^{2}}{R}, \end{matrix}

a (4) mozgásegyenlet mindkét oldalának abszolútértékét képezve

\begin{matrix} \frac{m_{e}}{\sqrt[]{1 - v^{2} / c^{2}}} \cdot \frac{v^{2}}{R} = e_{e} \cdot v \cdot B \cdot sin α \end{matrix}

adódik (

α

a sebesség és a mágneses indukció vektorának szöge, ez általában a pályagörbe mentén helyről helyre változik.) Azt kaptuk tehát, hogy

\begin{matrix} \frac{p}{e_{e} \cdot B} = R \cdot sin α . \end{matrix}

A fenti összefüggés jobb oldalán csak a pályagörbére jellemző mennyiségek szerepelnek, ha tehát azt akarjuk, hogy egy

e_{p} = - e_{e}

töltésű,

p

* impulzusú proton valamilyen

B

* mágneses térben ugyanazt a pályagörbét fussa be, mint az eddig vizsgált elektron, akkor a

\begin{matrix} B^{*} = - \frac{p^{*}}{p} \cdot B \end{matrix}

feltétel teljesülését kell (a pályagörbe minden pontjában) biztosítanunk. De mivel a mágneses indukció arányos a tekercsekben folyó áramokkal, a keresett feltétel

\begin{matrix} i_{k}^{*} = - \frac{p^{*}}{p} i_{k}, (k = 1,2, ..., n) . \end{matrix}

Az elektronok, illetve a protonok impulzusát a gyorsítófeszültségből számíthatjuk ki. A relativisztikus energiaképlet szerint

\begin{matrix} \frac{m_{e} \cdot c^{2}}{\sqrt[]{1 - v^{2} / c^{2}}} = m_{e} c^{2} + | e \cdot U | (= 2 \cdot m_{e} c^{2}), \end{matrix}

ahonnan

v = (\sqrt[]{3} / 2) \cdot c

, illetve

p = \sqrt[]{3} \cdot m_{e} \cdot c

adódik. A protonok sebességét és impulzusát a klasszikus mechanikai összefüggésből számíthatjuk, hiszen a proton tömege sokkal nagyobb, mint az elektroné, s emiatt (ugyanakkora gyorsítófeszültség hatására) sokkal kisebb sebességre gyorsulnak csak fel.

\begin{matrix} m_{p} \frac{v^{* 2}}{2} = \frac{p^{* 2}}{2 m_{p}} = | e_{p} \cdot U | = 511 keV \approx m_{e} \cdot c^{2}, \end{matrix}

innen

\begin{matrix} p^{*} = \sqrt[]{2 m_{e} \cdot m_{p}} \cdot c, \end{matrix}

s végül az impulzusok nagyságának aránya

\begin{matrix} \frac{p^{*}}{p} = \sqrt[]{\frac{2}{3} \cdot \frac{m_{p}}{m_{e}}} = \sqrt[]{\frac{2}{3} \cdot \frac{938 MeV}{0, 511 MeV}} \approx 35, 0. \end{matrix}

Az eltérítő tekercsek áramát tehát az

i^{*} = - 35, 0 i

összefüggés szerint kell módosítanunk, ha elektronok helyett protonnyalábot akarunk fókuszálni.
b) A mikroszkóp felbontóképessége a részecskék Broglie-hullámhosszával, az pedig az impulzus reciprokával arányos. Az előző számítás szerint a protonok impulzusa kb.

35

-ször nagyobb, mint az elektronoké, a szóban forgó protonmikroszkóppal tehát akár

35

-ször kisebb tárgyakat is megfigyelhetünk, mint az eredeti elektronmikroszkóppal.

4. feladat (mérési feladat.) Adott az alábbi felszerelés:
1. Két, egyenként

10 mm

vastag piezoelektromos korong, amelyeknek oldallapjaira elektródákat párologtattak (lásd a 3. ábrát). Ezek egy tolómérő száraira vannak erősítve.
2. Hitelesített szinuszjel-generátor.
3. Két bemenetű (kétcsatornás) oszcilloszkóp.
4. Két, folyadékot tartalmazó, zárt műanyag zacskó.
5. Egy pohárban glicerin, amely arra való, hogy a piezoelektromos korong lapjait ezzel bekenve jobb mechanikai csatlakozás jöjjön létre.
6. Kábelek és egy elosztó.
7. A folyadékkal telt zacskók rögzítésére szolgáló állvány.
8. Tolómérőtartó.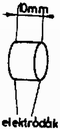

3. ábra

Elektromos mező hatására a piezoelektromos anyagok megváltoztatják hosszméretüket, és viszont: deformációk hatására a piezoelektromos anyagban elektromos mező jön létre. Ezért egy piezoelektromos anyagban váltakozó elektromos mező segítségével mechanikai rezgéseket lehet kelteni, vagy mechanikai rezgésekkel váltakozó elektromos tér hozható létre.

a) Annak ismeretében, hogy a longitudinális ultrahang sebessége a korong anyagában kb.

4000 m/s

, adjál durva becslést a korong szimmetriatengelyével párhuzamos mechanikai rezgések rezonanciafrekvenciájára. Feltételezzük, hogy a korong rögzítése nem befolyásolja a rezgéseket. (Megjegyezzük, hogy másfajta rezgések is létrejöhetnek a korongban, az előbbinél alacsonyabb, illetve magasabb frekvenciákkal.)
Előző becslésedből kiindulva határozd meg méréssel azt a frekvenciát, amelynél a piezoelektromos korongok a lehető legjobban működnek ultrahangot kibocsátó és (a folyadékon áthaladt ultrahangot) érzékelő rendszerként. Ha glicerinnel kenjük be a korongok felületét, mielőtt hozzányomjuk őket a műanyag zacskóhoz, ez javítja az ultrahang áthaladását.
b) Határozd meg az ultrahang sebességét mindkét folyadékban a zacskók kinyitása nélkül, és végezz hibabecslést!
c) Számold ki a két folyadékban megmért sebességek arányát, és gondosan add meg ennek is a hibáját!

Megoldás. a) A piezokristályban az alkotóval párhuzamosan terjedő rezgésekre a korong lapjai szabad végként viselkednek. A legalacsonyabb rezonancia frekvencia esetén

h = λ_{p} / 2 = v_{p} / (2 f)

, ahol

h

a korong magassága,

λ_{p}

v_{p}

és

f

pedig az ultrahang hullámhossza, sebessége és frekvenciája a piezokristályban. A keresett frekvenciára számadatainkkal

f = 2 \cdot 10^{5} Hz

adódik. Ez az érték csak egy becslés, hiszen a korong átmérője nem sokkal nagyobb a magasságánál, és ez befolyásolhatja a rezgést.

4. ábra

A mérési elrendezést a 4. ábra mutatja. A szinuszjel-generátor egyrészt az egyik piezo korongra van kötve (ez bocsátja ki az ultrahangot), másrészt az oszciloszkóp egyik bemenetére. A másik piezo korong, amely mikrofonként működik, az oszcilloszkóp másik bemenetére van kötve. Mindkét korong kissé hozzá van nyomva az egyik folyadékot tartalmazó zacskóhoz. A frevenciát a

100

‐

1000

kHz tartományban lassan változtatva a felfogott jel amplitúdója egy éles csúcsot mutat az

f = 215 kHz

frekvencián. Ezt a frekvenciát a legpontosabban (

3

kHz pontossággal) úgy határozhatjuk meg, hogy az oszcilloszkóp ernyőjéről leolvassuk néhány periódus hosszát.
b) Ha a tolómérő segítségével változtatjuk a két piezo korong távolságát, akkor változik az az út, amit az ultrahang a folyadékban megtesz, és így az oszcilloszkópra érkező két szinuszjel fáziskülönbsége. A tolómérő nyílását változtatva az elmozdulást (

d

) minden olyan pontban leolvassuk, ahol a két jel azonos fázisban érkezik az oszcilloszkópra. Ábrázolva az

n

hullámhossznyi elmozdulásnál leolvasott

d_{n}

értékeket, a kapott pontok közelítőleg egy egyenesre illeszkednek (5. ábra). Az egyenes meredeksége éppen a hullámhosszt adja, amelyre

λ_{A} = 7, 010 \pm 0, 035 mm

és

λ_{B} = 8, 950 \pm 0, 045 mm

adódik. Az ultrahang sebessége a folyadékban

v = λ f

, adatainkkal

v_{A} = 1508 \pm 30 m/s

v_{B} = 1923 \pm 38 m/s

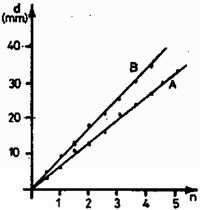5. ábra

c) A két sebesség aránya

v_{B} / v_{A} = λ_{B} / λ_{A} = 1, 276 \pm 0, 013

, itt a frekvenciamérés pontatlansága nem játszik szerepet.