Kezdőlap


Cím:	1988. évi Eötvös Loránd Fizikaverseny
Szerző(k):	Radnai Gyula
Füzet:	1989/október, 327 - 330. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1988. október 28-án rendezte 65. versenyét Budapesten és 12 vidéki városban. A versenyen az 1988-ban érettségizettek és középiskolai tanulók vehettek részt. A versenyzőknek 5 óra állt rendelkezésükre, bármilyen segédeszközt használhattak. Összesen 289 versenyző adott be dolgozatot. A feladatok kitűzését és a beadott megoldások értékelését a Versenybizottság közösen végezte; vezetője Vermes Miklós visszavonulását követően Radnai Gyula, tagjai Boros János, Gnädig Péter és Károlyházy Frigyes voltak. Ismertetjük a feladatokat és a verseny végeredményét.

1. Két egyforma pénzérméből egy rájuk ragasztott hurkapálca segítségével ,,lapos súlyzót'' készítünk. A súlyzót az asztal szélére helyezzük, és az egyik érmének egy ütéssel a súlyzó tengelyére merőleges kezdősebességet adunk. Az ütést akkorára választjuk, hogy a súrlódás a súlyzót egy negyed fordulat megtétele után állítsa meg.
Elkanyarodik, vagy egyenes vonalban mozog a súlyzó tömegközéppontja ? (1. ábra)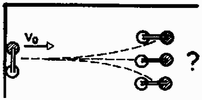

1. ábra

Megoldás. Tekintsünk egy ellökés utáni, de megállás előtti pillanatot ! A helyzetet a 2. ábra mutatja. Az ábrán

A

jelöli a meglökött érme tömegközéppontját,

B

a másikét.

K

a súlyzó tömegközéppontja (

A B

felező pontja).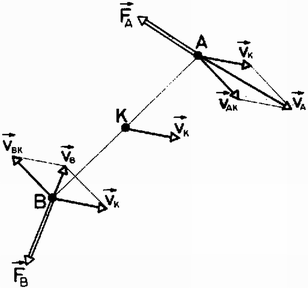

2. ábra

A súlyzó bármely pontjának mozgása két jellegzetes mozgásból tehető össze: az egyik a tömegközépponttal együtt történő haladó mozgás, ezt a pillanatnyi sebességet jelöli

{\vec{v}}_{K}

az ábrán;
a másik a tömegközéppont körüli forgás, az ennek megfelelő pillanatnyi sebesség

A

-nál

{\vec{v}}_{A K}, B

-nél pedig

{\vec{v}}_{B K}

.
A meglökött érme sebessége az asztalhoz képest

{\vec{v}}_{A}

, a másik érme sebessége az asztalhoz képest

{\vec{v}}_{B}

.
A súrlódási erő mindkét érme esetén a sebességgel ellentétes irányú, de nagyságuk egyenlő, mivel a felületre merőleges nyomóerők egyenlők.
Mivel

{\vec{v}}_{A K}

és

{\vec{v}}_{K}

hegyesszöget,

{\vec{v}}_{B K}

és

{\vec{v}}_{k}

pedig tompaszöget alkot, ezért

{\vec{v}}_{A}

kisebb szöget zár be

{\vec{v}}_{K}

-val, mint

{\vec{v}}_{B}

.
Így az eredő erő ,,hátrafelé'' és a rajzon ,,lefelé'' mutat (3. ábra), tehát a tömegközéppont jobbra kanyarodik el.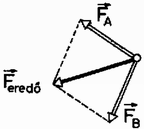

3. ábra

Megjegyzés. A fenti megfontolás során a pénzérmék méretét elhanyagoltuk. A valóságban a ,,forogva haladó'' pénzérmére ható súrlódási erő (a pénzérme különböző részeire ható súrlódási erők eredője) függ a tömegközéppont sebességétől. Ez a hatás éppen a megoldásban tárgyalt effektus ellen dolgozik, de elegendően hosszú hurkapálca esetén teljes mértékben elhanyagolható.

2. Az a élhosszúságú szigetelő kockára lapátlók mentén vezetett huzalból ‐ az ábra szerint ‐

R

ellenállású áramkört illesztünk.

B

erősségű homogén mágneses mezőt kapcsolunk be, rendre a kocka egyes lapjaira merőleges irányokban (4. ábra).
a) Mekkora töltés halad át az egyes esetekben a huzal keresztmetszetén ?
b) Haladhat- e át ezeknél is több töltés, valamilyen ,,ferde'' irányú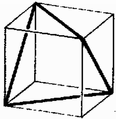

B

esetén ?

4. ábra

Megoldás. A huzal tetszőleges keresztmetszetén áthaladó töltés az alábbi módon számítható ki:

\begin{matrix} Δ Q = I \cdot Δ t = \frac{U}{R} Δ t = \frac{Δ Φ}{R} = \frac{B \cdot A}{R}, \end{matrix}

ahol

A

jelenti a hurok

B

-re merőleges vetületének területét.
A kocka egyes lapjaira merőleges irányokban az 5. ábrán vázolt vetületeket kaphatjuk.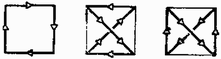

5. ábra

Amikor a vetület egy

a

oldalú négyzet, akkor az áthaladó töltés:

\begin{matrix} Δ Q = \frac{B \cdot a^{2}}{R} . \end{matrix}

A másik két esetben a vetület két egybevágó háromszög, melyek ,,körüljárási iránya'' azonban ellentétes, így a két terület előjeles összege zérus. Ezekben az esetekben tehát

\begin{matrix} Δ Q = 0. \end{matrix}

Most vizsgáljuk meg, hogy valamilyen ferde irányú

B

esetén haladhat-e át több töltés, mint az előbb kiszámított

\frac{B \cdot a^{2}}{R}

.
Vegyünk fel egy derékszögű koordinátarendszert úgy, hogy a tengelyek legyenek párhuzamosak a kocka éleivel, és mondjuk

x

irányból nézve legyen a hurok vetülete az

a

oldalú négyzet (6. ábra).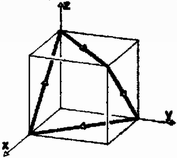

6. ábra

Ekkor az indukcióvektor komponenseit

B_{x}

-szel,

B_{y}

-nal, ill.

B_{z}

-vel jelölve az áthaladt töltés:

\begin{matrix} Δ Q = \frac{B_{x} A_{x} + B_{y} A_{y} + B_{z} A_{z}}{R}, vagyis \\ Δ Q = \frac{B_{x} a^{2}}{R} + 0 + 0, mivel A_{y} = 0 és A_{z} = 0. \end{matrix}

Minthogy

B_{x} \leq B

ezért

\begin{matrix} Δ Q \leq \frac{B a^{2}}{R}, \end{matrix}

tehát semmilyen ferde irányú

B

esetén nem haladhat át több töltés.
Ugyanerre az eredményre jutunk természetesen akkor is, ha a hurok különböző irányú vetületeit hasonlítjuk össze. Ebben az esetben még be kell bizonyítani, hogy a hurok semmilyen vetületének területe sem lehet nagyobb

a^{2}

-nél. Ebből azután már következik a bizonyítandó állítás:

\begin{matrix} Δ Q = B \end{matrix}

Megjegyzés. Annak bizonyítása, hogy a vetület területe nem lehet nagyobb

a^{2}

-nél, történhet például azon felismerés alapján, hogy a fenti hurok egy olyan térbeli négyszöget alkot, amelynek nemcsak oldalai, de átlói is

a \cdot \sqrt[]{2}

hosszúságú lapátlók. Az átlók vetületei lesznek a vetületnégyszög átlói. Így a vetületnégyszög átlói sem lehetnek

a \cdot \sqrt[]{2}

-nél hosszabbak. Mivel egy síkbeli négyszög területe nem lehet nagyobb, mint az átlók szorzatának a fele, ezért a vetület területe legfeljebb

\begin{matrix} \frac{a \sqrt[]{2} \cdot a \sqrt[]{3}}{2} = a^{2} \end{matrix}

lehet.

3. Egy pontszerű monokromatikus fényforrás és egy ernyő között átlátszatlan, fekete lemez van, rajta két parányi környílás. Fény csak ezeken a nyílásokon át juthat az ernyőre. Az ernyőn interferenciacsíkok jelennek meg.
Elhelyezhetünk-e ‐ ha igen, hogyan ‐ egy síktükröt úgy, hogy az ernyő megvilágítása
a) nagyjából egyenletes legyen;
b) közel zérus legyen ?

Megoldás. Mindkét eset elérhető, megvalósítható, ha a tükröt az átlátszatlan, fekete lemeznek azon az oldalán helyezzük el, ahol a fényforrás is van. Ekkor ugyanis már magán a fekete lemezen is létrejön interferencia a közvetlenül és a tükörről visszaverődve odaérő fény között.
a) Az ernyő megvilágítása nagyjából egyenletes lesz, ha az ernyőre csak az egyik parányi környílásból esik fény. Ehhez a tükröt úgy kell beállítani, hogy a direkt és a visszavert fény interferenciájának eredménye az egyik parányi környílás helyén kioltás legyen, a másiknál viszont nem. Ekkor ez utóbbi az egyetlen környílás, melyen át fény jut az ernyőre. A ,,parányi'' jelző utal arra, hogy a nyílás mérete olyan kicsi, hogy a nyíláson létrejövő elhajlás okozta intenzitásváltozás csekély. Az ernyő megvilágítása nagyjából egyenletes.
b) Az ernyő megvilágítása közel zérus lesz, ha a tükröt úgy állítjuk be, hogy a direkt és a visszavert fény interferenciájának eredménye mindkét parányi környílás helyén kioltás lesz. Ez megtehető, mert a kioltások nemcsak egy-egy pontban, hanem egy-egy görbe mentén jönnek létre, s akár az is elérhető, hogy az egyik ,,sötét csík'' áthaladjon mindkét környíláson. Mivel azonban a tökéletes kioltás szigorúan véve csak egy zérus szélességű vonal mentén valósul meg, s a környílás ugyan parányi, de nem zérus szélességű, ezért az ernyő megvilágítása nem tökéletesen zérus, hanem csak közel zérus lesz.

Megjegyzés. A feladatnak van egy ,,triviális'' megoldása is. Ha a tükröt árnyékoló lemeznek használjuk, és eltakarjuk vele egyik, illetve mindkét nyílást, előáll a feladatban megfogalmazott a), illetve b) eset. Ezt a megoldást mégsem lehet teljes értékűnek elfogadni, hiszen például a b) kérdés csak ,,közel zérus'' megvilágítást ír elő, nem pedig teljes sötétséget. Arról nem is beszélve, hogy a fizikában a tükröt tükörként illik felhasználni. Tudták ezt a versenyzők is, meg is írták többen, hogy csak azért adják ezt a megoldást, mert jobb nem jut az eszükbe. Az igazi megoldásra kevesen találtak rá.

A verseny eredménye

I. díjat kaptak egyenlő helyezésben:
Fucskár Attila, az ELTE programozó matematikus hallgatója, aki a budapesti Kaffka Margit Gimnáziumban érettségizett, mint Jánosi Ilona tanítványa, és Hauer Tamás, az ELTE fizikus hallgatója, aki a budapesti Apáczai Csere János Gimnáziumban érettségizett, tanára Kelemen László.

II. díjat kaptak egyenlő helyezésben:
Csahók Zoltán, az ELTE fizikus hallgatója, aki a budapesti Fazekas Mihály Gimnáziumban érettségizett, mint Horváth Gábor tanítványa, Demeter Gábor, a budapesti Móricz Zsigmond Gimnázium IV. osztályos tanulója, tanára Tarnóczyné Gegedon Melitta, és Szabó Szilárd, a budapesti Apáczai Csere János Gimnázium IV. osztályos tanulója, tanára Holics László.

III. díjat kaptak egyenlő helyezésben:
Csilling Ákos, a budapesti Fazekas Mihály Gimnázium III. osztályos tanulója, tanára Horváth Gábor, Keleti Tamás, az ELTE matematikus hallgatója, aki a budapesti Fazekas Mihály Gimnáziumban érettségizett, mint Horváth Gábor tanítványa, és Pásztor Gábor, a miskolci Földes Ferenc Gimnázium IV. osztályos tanulója, tanára Zámborszky Ferenc.

Dicséretet kaptak egyenlő helyezésben:
Lencse Gábor, a győri Révai Miklós Gimnázium IV. osztályos tanulója, tanárai Jagudits György és Takács István, valamint Somfai Ellák, a pápai Petőfi Sándor Gimnázium IV. osztályos tanulója, tanára Dankó Ferenc.
Az eredményhirdetésre 1988. november 25-én került sor az ELTE Múzeum körúti fizikai előadótermében. A nyertes versenyzőkön és tanáraikon kívül részt vettek az ünnepélyes díjkiosztáson a KöMaL 1987‐88. évi fizika pontversenyének legjobbjai is.
Valamennyi nyertes és helyezett versenyzőnek, valamint az őket felkészítő tanároknak ezúton is gratulálunk.