Kezdőlap


Cím:	1989. évi fizika OKTV
Szerző(k):	Szegedi Ervin , Ungár Péter , Vermes Miklós
Füzet:	1989/október, 321 - 327. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A verseny három csoportban folyt le. Az I. csoportban a szakközépiskolai tanulók versenyeztek. A II. csoportba tartozott minden alaptanterv szerint tanuló, fizikát fakultáción nem tanuló III. és IV. osztályos diák. A többi versenyző a III. csoportba tartozott. A II. és III. csoportban ugyanazok voltak a feladatok. A verseny első fordulója január 9-én, a második fordulója március 8-án és a harmadik fordulója április 25-én volt.

Az I. forduló feladatai a II. és III. csoportban

h

magasságból közvetlenül egymás után leejtünk egy

m_{1}

és egy

m_{2}

tömegű testet (1. ábra). Minden ütközés a függőleges egyenesben megy végbe és teljesen rugalmas.
a) A tömegek mely aránya esetén marad az ütközés után az

m_{1}

tömegű test nyugalomban ?
b) Ebben az esetben milyen magasra repül fel az

m_{2}

tömegű test ?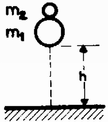

1. ábra

(Ungár Péter)

Megoldás. Mindegyik test

v_{0} = \sqrt[]{2 g h}

sebességgel érkezik a földhöz. Az

m_{1}

tömegű test

v_{0}

sebességgel indul felfelé és ütközik a lefelé

v_{0}

sebességgel érkező

m_{2}

tömegű testtel. Az ütközés utáni sebességek, a felfelé irányulókat pozitívnak számolva:

\begin{matrix} u_{1} = v_{0} \cdot \frac{m_{1} - 3 m_{2}}{m_{1} + m_{2}}, u_{2} = v_{0} \cdot \frac{3 m_{1} - m_{2}}{m_{1} + m_{2}} . \end{matrix}

a) A mi esetünkben

u_{1} = 0

, ebből következik, hogy

m_{1} / m_{2} = 3

.
b) Ekkor

u_{1} = 2 v_{0}

és a felfelé repülés magassága

4 h

.
A kísérlet folyamán a golyók összes mozgási és helyzeti energiája változatlan marad, mert a Föld nagy tömege folytán nem vesz fel mozgási energiát.

A

és

B

pontok távolsága

14

méter, a négy kötéldarab mindegyikének hossza

5

méter (2. ábra).

C

és

E

pontokban egy-egy

7

kg tömegű test lóg.

D

pontban olyan nagy

m

tömegű test függ, hogy ez a

D

pont

7 méterre

van az

A B

egyenes alatt. Az

m

tömegű testet lassan felemeljük, amíg

D

pont a

C

és

E

pontokkal egy magasságba jut. Mennyi munkát végeztünk ?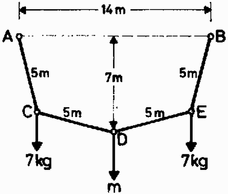

2. ábra

(Vermes Miklós)

Megoldás. Először meg kell állapítani az

m

tömeg nagyságát (3.a és 3.b ábra).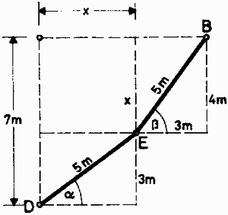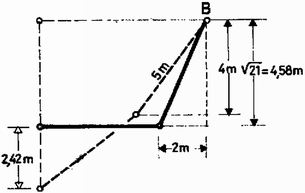

3.a ábra

3.b ábra

Az adatok szerint

5^{2} = x^{2} + {(7 - x)}^{2}

, innen

x = 4, tg α = 3 / 4

és

tg β = 4 / 3

.
Az első kötélben

(D E)

az erő

m g / (2 sin α)

, a második kötélben

(E B)

pedig

(m / 2 + 7) g / sin β

E

-ben a vízszintes összetevők egyenlők:

\begin{matrix} (\frac{m}{2} + 7) \cdot \frac{g}{sin β} \cdot cos β = \frac{m g}{2} \cdot \frac{1}{sin α} \cdot cos α; \end{matrix}

rendezve:

\begin{matrix} (\frac{m}{2} + 7) \cdot \frac{1}{tg β} = \frac{m}{2} \cdot \frac{1}{tg α} . \end{matrix}

A tangensek értékeit felhasználva:

8 m = \frac{9 m}{2} + 63

, innen

m = 18 kg

.
A geometriai viszonyokból látható, hogy a

18 kg

tömegű testet

2, 42

méterrel emeltük, ekkor a helyzeti energia növekedése

18 \cdot 2, 42 \cdot 9, 81 = 427

joule. A két

7

kg tömegű test

0, 58

méterrel süllyedt, így ezeknél a helyzeti energia csökkenése

2 \cdot 7 \cdot 0, 58 \cdot 9, 81 = 80

joule. A mi munkavégzésünk

427 - 80 = 347

joule.

150

voltra töltött

2 μ F

-os és

120 voltra

töltött

3 μ F

-os kondenzátor egy-egy ellentétes töltésű lemeze össze van kötve; a másik lemezeikből kivezető drótok szabadon végződnek (4. ábra). Ezekre a drótvégekre ráejtünk egy töltetlen

1, 5 μ F

-os kondenzátort.
a) Mekkora lesz ezután mindegyik kondenzátor feszültsége ?
b) Mennyi töltés megy át és merre az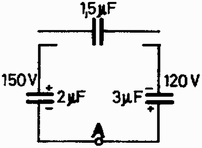

A

helyen ?

4. ábra

(Vermes Miklós)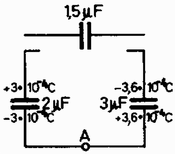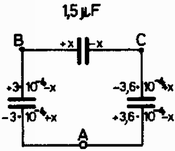

Megoldás. A ráejtett kondenzátornak

+ x

és

- x

töltése lett (pozitív töltésekkel számolva). Az 5.a ábra az eredeti állapotot tünteti fel.

5.a ábra

5.b ábra

A ráejtett kondenzátor töltései az 5.b rajzon látható módon változtatják meg a töltéseket.

B

és

A

között a feszültségkülönbség a bal oldali kondenzátoron át számítva:

\begin{matrix} + \frac{3 \cdot 10^{- 4} - x}{2 \cdot 10^{- 6}} . \end{matrix}

A feszültségkülönbség

A C B

úton számítva:

\begin{matrix} - \frac{3, 6 \cdot 10^{- 4} - x}{3 \cdot 10^{- 6}} + \frac{x}{1, 5 \cdot 10^{- 6}} . \end{matrix}

Ez a kettő egyenlő:

\begin{matrix} + \frac{3 \cdot 10^{- 4} - x}{2 \cdot 10^{- 6}} = - \frac{3, 6 \cdot 10^{- 4} - x}{3 \cdot 10^{- 6}} + \frac{x}{1, 5 \cdot 10^{- 6}} . \end{matrix}

Az egyenlet megoldása:

x = + 1, 8 \cdot 10^{- 4}

coulomb.

x

ismeretében kiszámíthatók a feszültségek: a

2 μ F

-os kondenzátoron

A

-hoz viszonyítva

+ 60

volt, a

3 μ F

-os kondenzátoron

- 60

volt, az

1, 5 μ F

-os kondenzátor két lemeze között

120

volt.
Az

A

helyen

1, 8 \cdot 10^{- 4}

coulomb ment át jobbról balra. A végső állapotot az 5.c ábra mutatja.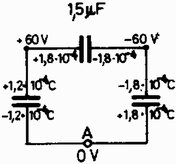

5.c ábra

4. Egy

76 cm

hosszú, felül zárt üvegcső alsó vége higanyba merül, a cső részben higannyal telt, felette az elzárt térben

0, 001

mol levegő van (6. ábra). A külső légköri levegő nyomása

76 cm

-es higanyoszloppal tart egyensúlyt. A levegő molhője állandó térfogaton

C_{v} = 20, 5 J/mol \cdot K

. Mennyi hőt ad le a csőbe zárt levegő, amikor hőmérséklete

10^{\circ} C

-kal süllyed?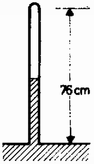

6. ábra

(Szegedi Ervin)

Megoldás. Az I. főtétel szerint:

Δ E = Δ Q + Δ W

, vagyis a gáz által felvett hő:

Δ Q = Δ E - Δ W

. Az energiaváltozás egyszerűen következik a hőmérsékletváltozásból:

\begin{matrix} Δ E = μ C_{v} (T_{2} - T_{1}) = 0, 001 \cdot 20, 5 \cdot (- 10) = - 0, 205 joule . \end{matrix}

A munkavégzés kiszámítására több eljárás lehetséges.
I. A bezárt levegő nyomását a levegőoszlop hossza jelenti, mert ezzel a nyomással nyomódott le a higany a

76 cm

-es magasságról (7. ábra).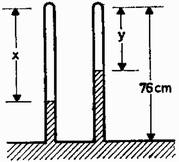

7. ábra

A munkavégzés

Δ W = p \cdot Δ V

. A mi esetünkben a nyomás a térfogattal lineárisan változik, ezért a kezdeti és végső nyomások középértékével számolhatunk:

\begin{matrix} p = \frac{p_{1} + p_{2}}{2} . \end{matrix}

A térfogatváltozás

Δ V = V_{2} - V_{1}

.
A gázon végzett munka:

Δ W = - \frac{1}{2} (p_{1} + p_{2}) \cdot (V_{2} - V_{1})

\begin{matrix} Δ W = - \frac{1}{2} (p_{2} V_{2} - p_{1} V_{1} + p_{1} V_{2} - p_{2} V_{1}) . \end{matrix}

A zárójelben levő harmadik és negyedik tag algebrai összege

0

, mert (a cső alapterületét

A

-val és a higany sűrűségét

ϱ

-val jelölve):

p_{1} V_{2} = ϱ g x \cdot A y

és

p_{2} V_{1} = ϱ g y \cdot A x

, és ezek egyenlők.
Az első két tagra a gáztörvényt alkalmazva

p_{2} V_{2} = μ R T_{2}

és

p_{1} V_{1} = μ R T_{1}

. A gázon végzett munka:

\begin{matrix} Δ W = - \frac{1}{2} \cdot μ R (T_{2} - T_{1}) = 0, 042 joule . \end{matrix}

II. A folyamat közben a nyomás és a térfogat egyenesen arányosak (politrop változás, 8. ábra).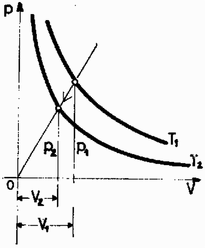

8. ábra

A nyomás

ϱ g x

, a térfogat

A x

, a gáztörvény szerint

p V = ϱ g x \cdot A x = ϱ g A x^{2} = μ R T

. A munkavégzést a trapéz területe jelenti:

\begin{matrix} Δ W = - \frac{1}{2} (p_{1} + p_{2}) (V_{2} - V_{1}) = - \frac{ϱ g A}{2} (x_{2}^{2} - x_{1}^{2}) . \end{matrix}

Az egyik metszéspontnál:

\begin{matrix} ϱ g A x_{1}^{2} = μ R T_{1}, x_{1} = \sqrt[]{\frac{μ R T_{1}}{ϱ g A}}, \end{matrix}

a másik metszéspontnál:

\begin{matrix} ϱ g A x_{2}^{2} = μ R T_{2}, x_{2} = \sqrt[]{\frac{μ R T_{2}}{ϱ g A}} . \end{matrix}

A gázon végzett munka:

\begin{matrix} Δ W = - \frac{ϱ g A}{2} (\frac{μ R T_{2}}{ϱ g A} - \frac{μ R T_{1}}{ϱ g A}) = - μ \frac{R}{2} (T_{2} - T_{1}) . \end{matrix}

A munkavégzés ismeretében a levegő hőfelvétele:

\begin{matrix} Δ Q = μ \cdot C_{v} (T_{2} - T_{1}) + μ \frac{R}{2} (T_{2} - T_{1}) = - 0, 205 - 0, 042 = - 0, 247 joule . \end{matrix}

Tehát a levegő

0, 247

joule hőt adott le.
A feladat érdekessége, hogy a kezdeti adatok kiesnek.

A II. forduló feladatai a II. és III. csoportban

1. A vízszintes síkban forgó

r = 10 cm

sugarú vékony gyűrűt

h = 20 cm

magasságból az asztalra ejtünk (9. ábra). Az elejtés pillanatában a gyűrű

ω_{0} = 21 s^{- 1}

szögsebességgel forog függőleges tengelye körül. Az ütközés rugalmatlan és igen rövid idő alatt megy végbe. A súrlódási tényező a gyűrű és az asztal között

μ = 0, 3.

Továbbá

g = 10 {m/s}^{2}

. Hány fordulatot tesz meg a gyűrű az elejtéstől számítva a megállásig ?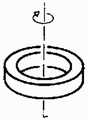

9. ábra

(Szegedi Ervin)

Megoldás. Az esés ideje

t_{0} = \sqrt[]{2 h / g} = 0, 2 s

, az esés végsebessége

v = g t_{1} = 2 m/s

. Az esés közben a gyűrű szögelfordulása

φ_{0} = ω_{0} \cdot t_{0} = 4, 2

.
Az ütközés igen rövid ideje alatt a gyűrűt az asztalhoz nyomó erő

m v / Δ t

, a súrlódási erő

μ m v / Δ t

, ennek forgatónyomatéka

μ r m v / Δ t

. Mivel az ütközés ideje igen rövid, ezért a súrlódási erő számítása közben a súly elhanyagolható. A gyűrű tehetetlenségi nyomatéka

Θ = m r^{2}

. Az ütközés közben a fékező szöggyorsulás

β = μ r m v / Θ Δ t = μ v / r Δ t

. Az ütközés közben

Δ t

idő alatt a szögsebesség csökkenése

Δ ω = β \cdot Δ t = μ v / r = 6 s^{- 1}

. Eközben a szögelfordulás az idő rövidsége miatt elhanyagolható.
Az ütközés után a szögsebesség

ω_{1} = ω_{0} - 6 = 21 - 6 = 15 s^{- 1}

. Ezután az asztalon fekvő gyűrű forgása fékeződik, a fékező erő

μ m g

, ennek forgatónyomatéka

μ m g r

. A fékező szöggyorsulás

β_{1} = μ m g r / Θ = μ g / r = 30 s^{- 2}

. A megállásig eltelt idő

t_{1} = ω_{1} / β_{1} = 0, 5 s

. Ezalatt a szögelfordulás

β_{1} t_{1}^{2} / 2 = 3, 75

.
A teljes szögelfordulás

4, 2 + 3, 75 = 7, 95

, a megtett fordulatok száma

7, 95 / 2 π =

= 1, 265

2. Egy dugattyús hengerben

4 gramm

hélium és

16 gramm

oxigén van elzárva

0^{\circ} C

hőmérsékleten és

10^{5} Pa

nyomáson (10. ábra). A henger fala és a dugattyú hőszigetelő. A nyomást

2 \cdot 10^{5} Pa

-ra fokozzuk. Mennyi lesz ezután a gázkeverék hőmérséklete és térfogata ? A hélium molhői

C_{v h} = 12, 3 J/mol \cdot K, C_{p h} = 20, 5 J/mol \cdot K;

az oxigén molhői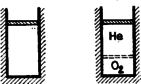

C_{v o} = 20, 5 J/mol \cdot K, C_{p o} = 28, 7 J/mol \cdot K.

10. ábra

(Vermes Miklós)

Megoldás. A héliumnak és az oxigénnek különböző

κ

fajhőhányadosa van, ezért az adiabatikus törvény

(p V^{κ} = konstans)

ugyanakkora nyomásváltozásnál az egyes gázok mindegyikére más térfogatot és ezzel együtt más hőmérsékletet jelent.
Helyezzünk el gondolatban egy hőszigetelő dugattyút az össze nem keveredett hélium és oxigén közé. Először megvizsgáljuk, hogyan változnak a kétféle gáz adatai a nyomás fokozása következtében.
A hélium számára

V_{h 1} = 22, 4 {dm}^{3}, κ_{h} = 5 / 3

és az új térfogat

V_{h 2}

. Az adiabatikus törvény szerint

10^{5} \cdot {22, 4}^{5 / 3} = 2 \cdot 10^{5} \cdot V_{h 2}^{5 / 3}

. Innen az összenyomott hélium térfogata

V_{h 2} = 14, 778 {dm}^{3}

. A gáztörvénnyel számíthatjuk a hélium hőmérsékletét az összenyomás után

(T_{h 2})

\begin{matrix} 10^{5} \cdot 22, 4 / 273 = 2 \cdot 10^{5} \cdot 14, 778 / T_{h 2}, innen T_{h 2} = 360, 26 K . \end{matrix}

Az oxigén számára

V_{o 1} = 11, 2 {dm}^{3}, κ_{o} = 1, 4

és az új térfogat

V_{o 2}

. Az adiabatikus törvény szerint

10^{5} \cdot {11, 2}^{1, 4} = 2 \cdot 10^{5} \cdot V_{o 2}^{1, 4}

. Innen az összenyomott oxigén térfogata

V_{o 2} = 6, 826 {dm}^{3} .

A hőmérséklete a gáztörvénnyel számítva:

\begin{matrix} 10^{5} \cdot 11, 2 / 273 = 2 \cdot 10^{5} \cdot 6, 826 / T_{o 2}, innen T_{o 2} = 332, 77 K . \end{matrix}

Ezután elvesszük a gondolatban behelyezett középső dugattyút, ekkor a két gáz keveredik állandó nyomás mellett és közös

T

hőmérséklete lesz.

\begin{matrix} 1 \cdot 20, 5 \cdot (360, 26 - T) = 0, 5 \cdot 28, 7 (T - 332, 77) . \end{matrix}

Ebből következik a gázkeverék végső hőmérséklete:

T = 348, 94 K

. A gázkeverékben levő hélium térfogata:

\begin{matrix} \frac{10^{5} \cdot 348, 94 \cdot 22, 4}{2 \cdot 10^{5} \cdot 273} = 14, 314 {dm}^{3} . \end{matrix}

A gázkeverékben levő oxigén térfogata:

\begin{matrix} \frac{10^{5} \cdot 348, 94 \cdot 11, 2}{2 \cdot 10^{5} \cdot 273} = 7, 157 {dm}^{3} . \end{matrix}

A kísérlet végén a gázkeverék együttes térfogata

14, 314 + 7, 157 = 21, 471 {dm}^{3} .

A keveredés folyamán a hélium leadott mozgási energiát az oxigénnek, mert az oxigén molekulái ugyanazon a hőmérsékleten több energiát igényelnek, mint a hélium molekulái, mert a repülésen kívül forognak is.

Megjegyzés: A gázkeverék adiabatikus változására vonatkozó Poisson-törvény általános esetre levezetve így szól: Ha adva van

n_{1}

mol gáz, amelynél

κ_{1}

és

n_{2}

mol gáz, amelynél

κ_{2}

érvényes, akkor

\begin{matrix} p V^{(\frac{n_{1} C_{p 1} + n_{2} C_{p 2}}{n_{1} C_{v 1} + n_{2} C_{v 2}})} = konstans. \end{matrix}

3. Egy lezárt doboz két kivezetésére különböző körfrekvenciájú váltófeszültségeket kapcsoltunk, és a következő váltóáramú ellenállásokat mértük:

\begin{matrix} \begin{matrix} ω [s^{- 1}] & 20 & 200 & 250 & 300 & 325 & 350 & 400 & 1000 & 5000 \\ Z [Ω] & 782 & 53, 0 & 34, 0 & 25, 4 & 25, 2 & 27, 2 & 34, 9 & 145, 5 & 792 \end{matrix} \end{matrix}

Mi van a dobozban ?
(Vermes Miklós)

Megoldás. Mivel a váltóáramú ellenállásnak minimuma van, ezért kondenzátort és önindukciós tekercset sorba kapcsolva tartalmaz a doboz (11. ábra). A rezonanciafrekvenciánál az ellenállás nem nulla, ezért sorba kapcsolt ellenállás is szerepel.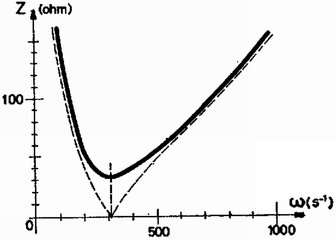

L

induktivitást,

C

kapacitást és

R

ellenállást sorba kapcsolva a váltóáramú ellenállás:

\begin{matrix} Z = \sqrt[]{R^{2} + {(\frac{1 - ω^{2} L C}{ω C})}^{2}} . \end{matrix}

11. ábra

Megtehetnénk, hogy az értéktáblázat három adatpárját felhasználva három egyenletet írunk fel és az egyenletrendszert megoldjuk. Ez igen fárasztó számolást jelentene, elfogadható pontossággal egyszerűbben is eljárhatunk.
Rezonancia esetén

Z = R

. Az ellenállás minimuma kb.

R = 25

ohm. Ezzel ismerjük az ohmos ellenállást. (A rezonanciához tartozó körfrekvencia

ω = 310 s^{- 1}

.)

Igen kis frekvenciánál szinte csak a kondenzátor okoz ellenállást:

\begin{matrix} 782 = \frac{1}{20 C}, \end{matrix}

innen

C = 63, 9 μ F

.
Igen nagy frekvencia esetében csak az önindukciós tekercs okoz lényeges ellenállást:

\begin{matrix} 792 = 5000 L, \end{matrix}

innen

L = 0, 158 henry

Megjegyzés: A táblázat kiszámításakor használt adatok:

C = 63, 7 μ F, L = 0, 159 henry, ω = 314 s^{- 1} (f = 50 s^{- 1})

voltak.

III. forduló

A harmadik (kísérleti) fordulóban a versenyzőknek először egy fototranzisztor karakterisztikáját kellett meghatározni, majd e mérés adatait felhasználva üveglemezek fényvisszaverődésének és fényelnyelésének a tanulmányozása volt a feladat.
Vermes Miklós

Az 1989. évi OKTV eredménye
I. csoport

1. díj: Herbert Norbert (Pécs, Zipernovszky K. Műszaki Szki., IV. o. t., tanára: Kiss Jenő)
2. díj: Budai Zoltán (Budapest, Landler J. Híradástechn. Szki., IV. o. t., tanára: Barabás János)
3. díj: Karászi Péter (Debrecen, Mechwart A. Gépip. Szki., IV. o. t., tanára: dr. Kopcsa József)
A további helyezettek: 4. Szakáts Géza (Vác, Lőwy S. Ip. Szki., III. o. t., t: Arany Tóth László); 5. Hortoványi Ottó (Debrecen, Mechwart A. Gépip. Szki., III. o. t., t.: dr. Kopcsa József).
Elsőfokú dicséretet 15, másodfokú dicséretet 5 versenyző kapott.

II. csoport

1. díj: Károlyi Antal (Budapest, I. István Gimn., IV. o. t., tanára: Moór Ágnes)
2. díj: Hidvégi Zoltán (Budapest, Árpád Gimn., IV. o. t., tanára: Szűcs Zsuzsanna)
3. díj: Késmárki Szabolcs (Kecskemét, Bányai J. Gimn., IV. o. t., tanára: Borsos Ferenc)
A további helyezettek: 4. Mohácsi Péter (Budapest, I. István Gimn., IV. o. t., t.: Moór Ágnes); 5. Pátrovics Levente (Budapest, I. István Gimn., IV. o. t., t.: Moór Ágnes); 6. Komorowicz Erzsébet (Budapest, Fazekas M. Gimn., IV. o. t., t.: Tóth László); 7. Bordás Ferenc (Szeged, Radnóti M. Gimn., IV. o. t., t.: Győri István és Dudás Zoltánné); 8. Peták Attila (Budapest, Berzsenyi D. Gimn., IV. o. t., t: Hubert Györgyné); 9. Gerecs László (Pécs, Nagy Lajos Gimn., III. o. t., t.: Györkő Zoltánné); 10. Horváth Tibor (Kecskemét, Katona J. Gimn., o. t., t.: Kocsisné Domján Erzsébet és Sáró Péter).
Elsőfokú dicséretet 10, másodfokú dicséretet 7 versenyző kapott.

III. csoport

1. díj: Szabó Szilárd (Budapest, Apáczai Cs. J. Gimn., IV. o. t., tanára: Holics László)
2. díj: Hornig Rudolf (Budapest, Apáczai Cs. J. Gimn., IV. o. t., tanára: Flórik György)
3. díj: Felső Gábor (Budapest, Apáczai Cs. J. Gimn., IV. o. t., tanára: Flórik György)
A további helyezettek: 4. Lévay Ákos (Budapest, Apáczai Cs. J. Gimn., t.: Flórik György); 5. Péter Tamás (Budapest, Radnóti M. Gimn., IV. o. t., t.: Tomcsányi Péter); 6. Somfai Ellák (Pápa, Petőfi S. Gimn., IV. o. t., t.: Dankó Ferenc); 7. Gombos Béla (Budapest, Apáczai Cs. J. Gimn., IV. o. t., t.: Flórik György); 8. Csuka Zoltán (Budapest, Apáczai Cs. J. Gimn., IV. o. t., t.: Kelemen László); 9. Mimon Tibor (Pécs, Nagy Lajos Gimn., IV. o. t., t.: Kállai Miklósné); 10. Seres Árpád (Békéscsaba, Rózsa F. Gimn., IV. o. t., t.: Simon Imréné).
Elsőfokú dicséretet 11, másodfokú dicséretet 9 versenyző kapott.