Cím: 1989. A XXX. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Szerző(k):  Benczúr Péter ,  Fleiner Tamás ,  Pásztor Gábor ,  Pataki János 
Füzet: 1989/november, 348 - 354. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Bizonyítsuk be, hogy az {1,2,...,1989} halmaz előáll 117 darab olyan diszjunkt halmaz, A1,A2,...,A117 egyesítéseként, amelyekre teljesül, hogy a) mindegyiküknek 17 eleme van, továbbá, hogy b) mindegyikükben ugyanannyi az elemek összege.

 

Az ilyen típusú feladatokra általában kétféle megoldás lehetséges. Az egyik csak a felosztás létezését igazolja, a másik megkonstruálja a felosztást is. Én ez utóbbit választottam. Sikerült találnom egy olyan módszert, amely két lépésben elkészíti a kívánt felosztást. Könnyen ellenőrizhető, hogy 1989=17⋅117. Ezt felhasználva első lépésben soroljuk be a számokat az ábrán látható módon.
 
 
1. ábra
 

Minden sorban pontosan 17 szám van, ezek alkotnak egy csoportot. Az első sorban a számok összege éppen megfelelő. Maradt 116 sorunk. Vizsgáljuk meg ezeket párosával az ábra szerint. Az A és C-vel jelzett csoportokban az egy sorban lévő számok összege mindenütt 995⋅16, tehát ugyanannyi. Csak a B-vel jelzett részben a "középső'' satírozott elem változik. Minden egyes párban a B-ben lévő elem ugyanannyival tér el a 995-től, az egyikük nagyobb, a másikuk kisebb. Tehát két ilyen szomszédos sorban is megfelelő a számok együttes összege. Ha a szomszédos sorokat párosával rendbe tudjuk tenni, akkor készen is vagyunk.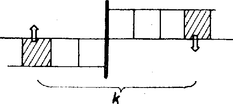
 
 
2. ábra
 

Második lépésben tehát vegyük azt a párt, ahol a középső B-beli elemnek a 995-től való eltérése éppen d. (d 1-től 58-ig változhat, mert 2⋅58+1=117). A pár első sorában a kívánt értéktől való eltérés d, a másodikban ‐ d. Ha a C-beli nyolcasokban kicserélünk az ábrán látható módon két számot, melyek egymástól k távolságra vannak (1≦k≦15), akkor az egyik sorban k-val nő, a másikban pedig k-val csökken az összeg. Ha 1≦d≦15, akkor így egyetlen cserével helyrehozható az eltérés. Ha az eltérés nagyobb 15-nél, akkor a két szélsőt kicseréljük, és a maradék 14 számmal tetszőlegesen megmaradó különbség helyrehozható 1-től 13-ig. Ha még ez sem elég, akkor a 14 szám közül a két szélsőt ismét cseréljük ki. A maradék 12 számmal tetszőlegesen megmaradó különbség korrigálható 1-től 11-ig. Látható, hogy C-beli elemek alkalmas cseréjével tetszőleges eltérés korrigálható az alábbi határig:15+13+11+...+3+1=64. Ez nagyobb mint 58, tehát mindegyik párnál elvégezhető a csere. Ezzel a feladatot megoldottuk.
 

(Pásztor Gábor)
 

2. A hegyesszögű ABC háromszög A-ból, B-ből és C-ből induló belső szögfelezői rendre az A1, B1, illetve C1 pontban metszik a háromszög körülírt körét. Az AA1 egyenest az A0 pontban metszi a B- és a C-beli külső szögfelező és hasonlóan kapjuk a B0 és a C0 pontokat. Bizonyítsuk be, hogy
i) az A0B0C0 háromszög területe egyenlő az AC1BA1CB1 hatszög területének kétszeresével;
ii) az A0B0C0 háromszög területe legalább négyszer akkora, mint az ABC háromszög területe.
 

Mivel a háromszög egy szögének külső és belső szögfelezője merőleges egymásra, az A,B,C pontok az A0B0C0 háromszögben a magasságvonalak talppontjai. Ismeretes, hogy egy háromszög Feuerbach-köre áthalad a magasságok talppontjain, az ABC háromszög köré írt köre tehát az A0B0C0 háromszög Feuerbach-köre. A Feuerbach-kör áthalad az OA0,OB0,OC0 felezőpontján is, ezért OA1=A1A0, OB1=B1B0, OC1=C1C0.
 
 
3. ábra
 

Jelöljük a kis háromszögek területét ti-vel (i=1,2,...12) az ábra szerint. Így t1=t7, mert a két háromszög alapja és magassága egyenlő. Ugyanígy kapjuk, hogy t2=t8, t3=t9, t4=t10, t5=t11, t6=t12. Ezeket összeadva:
t1+t2+...+t6=t7+t8+...+t12.

Mindkét oldalhoz hozzáadva az egyenlet bal oldalát:
2(t1+t2+...+t6)=t1+t2+...+t12
ami éppen a bizonyítandó állítás.
 

A második állítás igazolásához ezután elegendő belátni, hogy az AC1BA1CB1 hatszög területe legalább kétszerese az ABC háromszög területének.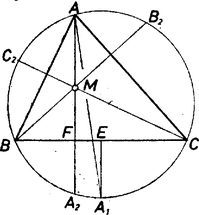
 
 
4. ábra
 

Jelöljük az ABC háromszög magasságpontjának az oldalakra vonatkoztatott tükörképeit rendre A2,B2,C2-vel. Ismert, hogy ezek a pontok a körülírt körön vannak. Az A1 pont a BC ív (A-t nem tartalmazó ívének) felezőpontja, mert BA1 és CA1 ívekhez tartozó kerületi szögek egyenlők, tehát az A1E szakasz (E a BC szakasz felezőpontja) nem kisebb az A2F szakasznál (F az A2 vetülete BC-re).
Ezért tBA1C≧tBA2C. Hasonlóan kapjuk, hogy tCB1A≧tCB2A, tAC1B≧tAC2B. Az egyenlőtlenségek megfelelő oldalait összeadva
tBA1C+tCB1A+tAC1B≧tBA2C+tCB2A+tAC2B.
A jobb oldalon éppen az ABC háromszög területe áll, mert a kis háromszögeket tükrözve az oldalegyenesekre A2, B2, C2 pontok tükörképe éppen a magasságpont, és így a tükörképek egyrétűen fedik le az ABC háromszöget.
Azaz
tBA1C+tCB1A+tAC1B≧tABC.
Mindkét oldalhoz hozzáadva tABC-t
tABC+tBA1C+tCB1A+tAC1B≧2tABC.
Így éppen a bizonyítandó állítást kapjuk, mert a bal oldal 4 háromszöge éppen lefedi az AC1BA1CB1 hatszöget.
Egyenlőség csak akkor állhat fenn, ha A1 és A2, B1 és B2, C1 és C2 egybeesik, ami azt jelenti, hogy a háromszög minden alapról nézve egyenlő szárú, tehát szabályos. Szabályos háromszögben pedig nyilván fennáll az egyenlőség.
 

(Pásztor Gábor)

3. Legyenek az n és a k adott pozitív egész számok, az S pedig olyan n-elemű síkbeli ponthalmaz, amelynek
a) semelyik három pontja nincs egy egyenesen;
b) az S halmaz minden P pontjához található legalább k darab S-beli pont, amelyek mind egyenlő távolságra vannak a P ponttól.
Bizonyítsuk be, hogy
k<12+2n.

Sajnos a feladatra a magyar versenyzők egyike sem talált megoldást ‐ utólag ez bizonyult a verseny legnehezebb feladatának.
A megoldás első lépése a bizonyítandó egyenlőtlenség valamivel megfoghatóbb, beszédesebb alakban történő felírása. Rendezés után négyzetre emelve
k2-k+14<2n,
azaz
k2-k2+18<n
adódik. A bal oldal első tagja egész, így elegendő igazolnunk, hogy
k2-k2≦n-1.

A bal oldalon éppen (k2), a k elem közül választható párok száma áll.
A halmaz minden P pontjához tekintsük tehát a tőle egyenlő távolságra lévő k darab S-beli pontból készíthető pontpárokat. Így összesen
n⋅(k2)
pontpárt kapunk. Ha most egy S-beli (A,B) pontpárt számba veszünk egy P pontnál, akkor a P rajta van az AB felezőmerőlegesén. Mivel az S-ben nincs három egy egyenesre eső pont, a fenti leszámolás során tetszőleges S-beli pontpárt legfeljebb kétszer kaphatunk meg, azaz
n⋅(k2)≦2⋅(n2)=n⋅(n-1),
ahonnan n-nel osztva éppen a bizonyítandó állítást kapjuk.
 

Megjegyzés. A feladat állítása úgy is teljesül, ha elhagyjuk azt a feltételt, hogy nincs három egy egyenesre eső S-beli pont, ennek bizonyítására most nem térünk ki.
(Pataki János)

 

4. A konvex ABCD négyszög AB, BC és AD oldalaira teljesül, hogy AB=AD+BC. A négyszög belsejében úgy helyezkedik el a P pont, hogy AP=h+AD és BP=h+BC, ahol h éppen a P pontnak a CD egyenestől mért távolsága. Bizonyítsuk be, hogy
1h≧1AD+1BC.

A 2. napon az első nap már elég jól bevált taktikát akartam követni, vagyis a geometria feladattal kezdeni. Az első sikertelen másfél óra után váltottam csak az 5. feladatra. Azt megoldva tértem vissza a 4.-re, és ez "be is jött''.
Az első nehézséget maga az állítás okozta. Mit kezdjek szakaszok négyzetgyökeinek reciprokával? Könnyebben értelmezhetőnek tűnt ehelyett a AD⋅BC≧h⋅AD+h⋅BC állítást igazolni. Ezeknek a következő geometriai jelentést tulajdoníthatjuk: könnyen ellenőrizhető, hogy 2xy nem más, mint x és y sugarú egymást kívülről érintő körök közös érintőszakasza.
A következő részcél ilyen körök keresése a négyszögben. Itt sikerült hasznosítanom az első másfél órám eredményeit is. Ez az idő a következő ötletre "ment rá''. Rögzítsük AD, BC hosszát, változtassuk h hosszát, majd egy-egy ((AD;BC;h) hármashoz próbáljunk ABCD négyszög(ek)et szerkeszteni.
Mivel AB=AD+BC; AP=AD+h; BP=BC+h, ezért ekkor az ABP háromszög megszerkeszthető. A C pont mértani helye a B körüli, BC sugarú kB kör, a D ponté a hasonló kA kör. A CD szakasz pedig érinti a P körüli, h sugarú kP kört. Megvan a három kör! Annak a feltétele, hogy létrejöjjön legalább egy ,,jó'' ABCD négyszög, az, hogy legyen a kP körnek olyan érintője, amelynek van közös pontja a kA és kB körökkel is, méghozzá úgy, hogy a metszéspontok az AB egyenes P felőli partján legyenek, (hogy a négyszög konvex legyen). Ehhez az nyilván elégséges, hogy kP teljesen az AB felőli partján legyen kA és kB közös külső érintőinek; legfeljebb érintse. De ez szükséges is, mert ellenkező esetben a következő igaz: a kA és kB bármely X, illetve Y pontját összekötve, ez a szakasz a közös érintő alatt AB felé eső részén) halad, így kP-t csak oly módon érintheti, ha P a létrejövő XYAB négyszög külső pontja.
 
 
1. ábra
 

Az volt az elképzelésem, hogy igazolom a AD⋅BC≧(AD+BC)h helyességét. Látható, hogy h változtatásával a bal oldal állandó, a jobb oldal pedig ugyanolyan irányban változik. Ha belátnánk, hogy h maximumakor egyenlőség áll fenn, akkor készen lennénk. Az 1. ábrát tanulmányozva észrevehetjük, hogy ha kP érinti kA és kB közös érintőjét, akkor RQ=2⋅AD⋅h; QZ=2⋅BC⋅h; RZ=2⋅AD⋅BC, és RQ+QZ=RZ. Azaz itt egyenlőség áll fenn. Vonzónak tűnik belátni, hogy h erre az esetre maximális. Ekkor már az egyenlőség feltétele is megvan: az ABCD derékszögű trapéz (ADC∢=DCB∢=90∘). Ezt nem túl elegáns úton sikerült befejeznem. Találhattam volna szebb módot is, de az elkövetkezőkben felhasznált részeredményeim már hamarabb elkészültek, így ez tűnt a leggyorsabb útnak.
Legyen koordinátarendszerünk középpontja az A pont, A(0;0); legyen AD=s, BC=z és feltehető, hogy BC≧AD. Mivel BP-AP=BC-AD= konstans, ezért h változtatásával P egy fél hiperbola ágon mozoghat (2. ábra). Ezen látszik, hogy ha x csökken, az y nő (ez az egyenessé torzult hiperbolánál (AD=BC) is elfogadható).  Belátjuk, hogy h növelésével x csökken (vagy állandó marad, az egyenes esetén ), azaz y nő. Így egyre feljebb kerül kP azon S pontja, amelyre SP⊥AB és S a P fölött van. Ez a pont tehát egyre feljebb kerül, de az érintőnél levő helyzetnél nem mehet tovább. Így valóban az érintőnél lesz h maximális.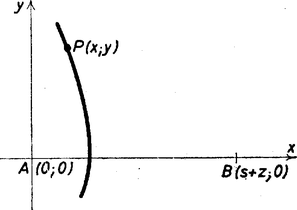
 
 
2. ábra
 

Ugyanakkor a P(x;y) pontra AP=s+h azaz
(1) x2+y2=(s+h)2; BP=z+h, azaz
(2) (s+z-x)2+y2=(z+h)2;
ezek különbségéből
 

x=(s+z)+(s-z)(s+z+2h)2(s+z).
 


Ez egy elsőfokú függvénye h-nak, és az együtthatója s-z2(s+z)≦0; azaz h növelésével y is nő. Vagyis állításunkat beláttuk.
 

(Benczúr Péter)

 
5. Bizonyítsuk be, hogy minden pozitív egész n-hez található n darab szomszédos pozitív egész szám úgy, hogy egyikük sem egyenlő egy prímszám pozitív egész kitevőjű hatványával.
 

Egy egész szám pontosan akkor nem prímhatvány, ha van két relatív prím valódi osztója. Keressük az n darab számot
{2+M,3+M,...,(n+1)+M}(1)
alakban.
Ha i|M, 2≦i≦n+1 esetén és M=i⋅mi, akkor
i+M=(1+mi).
Innen látszik, hogy ha még i|mi is teljesül, akkor
(i,1+mi)=1,
és így minden 1-nél nagyobb i-re i+M előáll két 1-nél nagyobb relatív prím szám szorzataként, tehát nem prímhatvány.
Ha tehát i2|M, i=2,3,...,n+1, akkor az (1) alatti számok egyike sem prímhatvány; a talált feltétel pedig biztosan teljesül az M=[(n+1)!]2 választással. Ezzel a bizonyítást befejeztük.
 

(Pataki János)

 
6. Az 1,2,...,2n-1,2n számok egy x1,x2,...,x2n-1,x2n permutációját nevezzük jónak, ha van olyan i∈{1,2,...,2n-1}, amelyre |xi-xi+1|=n.
 

Bizonyítsuk be, hogy minden pozitív egész n-re az 1,2,...,2n-1,2n számok összes permutációjának több mint a fele jó.
 
A megoldásból talán látható, miért ez a feladat tetszik legjobban az összes közül, hiszen elkerüli a leszámolást vagy a becslést. Eleinte én is becsülgetős, vagy indukciós megoldást akartam adni, azonban mikor ez nem sikerült, és a másik két feladat eléggé felbosszantott, úgy döntöttem, hogy ezt hamar megoldom, ami sikerült is. Eleinte magam sem akartam elhinni, hisz mégis a hatodik ‐ a zsűri által a legnehezebbnek tartott ‐ feladatról van szó, de sokszori átgondolás után sem találtam hibát, így kényszerűen elhittem, hogy elegáns megoldást leltem.
Megadok egy kölcsönösen egyértelmű megfeleltetést, mely a nem jó permutációkat leképezi a jók egy részhalmazára.
Minden 1≦i≦2n egész számra az i párjának nevezem azt a k egész számot, melyre 1≦k≦2n és |i-k|=n. Így az 1,2,...,2n számokat párokba soroltam. Tekintem a nem jó x1,x2,x3,...,x2n permutációt. Legyen az x2n párja xk.
Ekkor e rossz permutáció megfelelője az
x1,x2,...,xk,x2n,...,x2n-1

jó permutáció lesz, hisz |xk-x2n|=n. A nem jó permutációk megfelelői azon jó permutációk lesznek, melyekre
∃i∈{1,2,...,2n-1},hogy|xi-xi+1|=n
és ezen i-re, i≠2n-1, tehát egyetlen szomszédos pár nincs a permutáció végén. Az így kapott jó permutációk mindegyikéből rekonstruálható az eredeti nem jó, tehát a megfeleltetés valóban kölcsönösen egyértelmű.
Ez azt jelenti, hogy a nem jó permutációk száma azonos az előbbi típusú, jó, permutációk számával.
Ezen permutációk pedig kevesebben vannak, mint a jók, hisz az 1,n+1 végű jó permutációk nem tartoznak a rosszak képeihez.
 

(Fleiner Tamás)