| Cím: | Nehéz-e kommunikálni? | ||
| Szerző(k): | Lovász László | ||
| Füzet: | 1989/november, 337 - 346. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. Üzenetek nagyon távolra Valahol a világűrben egy űrhajó száguld a Mars felé. Kapcsolatban van a földi irányítóközponttal, ahol a nagy teljesítményű számítógépek hatalmas munkát végeznek, feldolgozzák a mérési eredményeket, pályakorrekciókat számolnak és így tovább. A kommunikáció viszont nagyon drága dolog, az üzeneteket kódolni kell, mindez időbe telik, sok energiát fogyaszt. Egyáltalán nem mindegy, hosszú vagy rövid üzeneteket váltanak-e a felek. Nagyon fontos kérdés, hogy miképpen lehet gazdaságosan kommunikálni; erről lesz szó az alábbiakban. Nézzünk először egy nagyon egyszerű alapfeladatot ebből a témakörből. Az űrhajó fedélzeti számítógépének alapprogramját időről időre ellenőrizni kell a Földön, hiszen a kozmikus sugárzás kárt tehet benne. Maga a program lényegében egy hosszú, nullákból és egyesekből álló sorozat; elvben semmi akadálya, hogy ezt a 0‐1 sorozatot sugározzák vissza a Földre, ahol aztán egybevethető az ott biztonságosan tárolt példánnyal. A gond csak az, hogy ez a sorozat rettenetesen hosszú ‐ mondjuk bitből áll ‐ a teljes sorozat visszaküldése tehát gyakorlatilag lehetetlen. Az első gondolatunk az lehet, hogy annak a természetes számnak a felhasználásával próbáljuk tömöríteni az információt, amelynek ez a 0‐1 sorozat a kettes számrendszerbeli alakja ‐ például úgy, hogy prímtényezőkre bontjuk és csak az ügyesen kódolt prímfelbontást sugározzuk vissza. Meg lehet azonban gondolni, hogy ezzel lényegében nem nyerhetünk, bitnél olcsóbban nem oldható meg a teljes információ visszaküldése. Hogy ne legyen az üzenet ilyen hosszú, valamiben engedni kell. Legyen ez a biztonság. Tegyük fel, hogy csak -os biztonsággal szeretnénk tudni, nem sérült-e meg a program. Ezt persze nem úgy érdemes csinálni, hogy a sorozat egy véletlenszerűen választott jegyét ‐ vagy jegyeit ‐ küldjük vissza ellenőrzésre, hisz ekkor jegyenként a valószínűsége, hogy hibás jegyre akadunk. Jelölje az űrhajó programjának megfelelő számot , a Földön tárolt szám pedig ‐ aminek tehát a valódi program a kettes számrendszerbeli alakja ‐ legyen . A módszer legyen a következő. A Földön választanak egy korlátot, legyen ez , majd később eldöntjük, mekkora legyen ‐ és ezután véletlenszerűen kiválasztanak egy prímszámot és között. Ezt elküldik az űrhajónak, ahol kiszámolják az maradékát -vel osztva ‐ legyen ez ‐ és ezt visszaküldik a Földre, ahol egybevetik az ott kiszámolt -gyel. Ha a két maradék nem egyenlő, akkor a program biztosan rossz. Elképzelhető azonban, hogy a maradékok egyenlők, és a program mégis rossz. Ez úgy lehetséges, ha a véletlenszerűen választott prímszám osztója az különbségnek. Próbáljuk megbecsülni, hogy mekkora lehet ennek a valószínűsége. Ha az -nél nem nagyobb prímek számát szokás szerint -nel jelöljük, akkor a szóban forgó valószínűség éppen
A kérdés úgy hangzik, hogy mekkorára válasszuk az értékét ahhoz, hogy a fenti valószínűség -nél kisebb legyen. A számlálóban és legfeljebb bitből álló számok, így A hiba valószínűségére innen a
Az űrhajó kommunikációs feladata az egyik fő forrása ezeknek a kérdéseknek. Egy másik ilyen forrás a nagyméretű integrált áramkörök vizsgálata. Ma már ott tart a technológia, hogy egy-egy chipen irdatlan mennyiségű áramköri elemet tudnak elhelyezni. Ezek között adott típusú huzalozást kell építeni. Kiderült, hogy az áramkör méretének a csökkentése során ‐ a működés sebességének növeléséhez erre szükség van, hisz elvi korlát az áram terjedésének a sebessége ‐ ezeknek a huzalozásoknak a tervezése az egyik legnagyobb probléma. Az áram nyomán ugyanis hő fejlődik, és így kis térfogatra nem lehet túl hosszú huzalrendszert bezsúfolni. Nézzük a következő, a korábbira némileg emlékeztető feladatot. Olyan áramkört kell terveznünk, amely két -hosszúságú bitsorozatról eldönti, egyenlők-e, vagy sem ‐ tehát a földi ellenőrzés feladatát valósítja meg. Az áramköri egységekről feltesszük, hogy rendkívül egyszerű "szerkentyűk'', egy-vagy két bejövő bitet tudnak kezelni, ezekből kiszámolnak valamit, és továbbküldik egy következő processzornak. Az 1. ábrán látható egyszerű berendezés például a következőképpen oldja meg a feladatot. Kezdetben minden processzor "alszik'', kivéve -et. 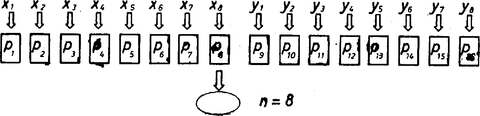 Az első taktusra a processzor ‐ az ábrán ‐ leolvassa az bitet, elküldi balra és egyidejűleg jobbra küld egy "ébresztő'' szignált. A következő lépésben a felébresztett leolvassa -t, balra küldi -nek és felébreszti -at. Általában a processzorok a jobbról érkező jeleket a következő taktusban balra küldik tovább, ezen kívül balról érkező szignál hatására a második darab processzor mindegyike a következő lépésben a bejövő bitet balra küldi, és jobbra küld egy szignált. Ennél bonyolultabb működést nincs okunk feltételezni a processzorainkról. Ennek hatására a beérkező jelek "egyes térközzel'' masíroznak balra. Amikor a megkapja -et, leolvassa -et és összehasonlítja őket; jobbra küld egy -est, ha ezek egyenlők és -át, ha nem. Ez a jel épp akkor érkezik -be, amikor az jobbról megkapja -t. Ez a processzor kiszámolja az összehasonlítás eredményét és jobbra küldi a szorzatot. Ez akkor és csak akkor lesz , ha és . Nyilvánvaló, hogy a processzor tudja majd a teljes választ: ott ismerjük meg a szorzat értékét, ami pontosan akkor , ha a két sorozat bitről bitre azonos. A dolog tényleg igen egyszerű, egyetlen hátulütője, hogy kicsit lassú. Elég sokáig vándorolgatnak a jelek, látható, hogy éppen 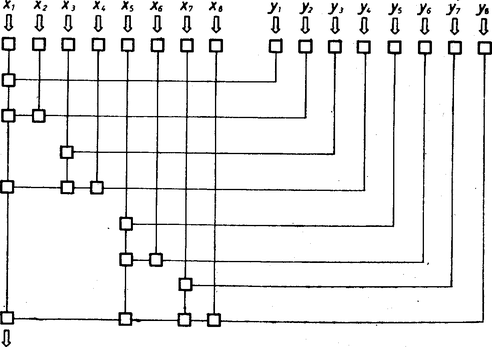 Az egyszerűség kedvéért tegyük fel, hogy az kettőhatvány ‐ a gyakorlatban úgyis ez a helyzet. Ekkor a 2. ábra első átlójában levő processzor mindegyike összehasonlítja a megfelelő -t és -t ‐ egyetlen taktusban szimultán ‐ majd az átlóként feleződő számú processzorok ezeket a részeredményeket dolgozzák fel, és végül a -edik taktusban a bal alsó processzor a teljes választ ismeri. A feldolgozáshoz szükséges idő így -re rövidült, ennek viszont az lett az ára, hogy a huzalrendszer összhossza megnőtt. Könnyű számolási gyakorlat, hogy a terület ‐ így hívják a drótok hosszának összegét ‐ most körülbelül . Felvetődik a kérdés, készíthető-e jobb áramkör ennek a feladatnak a megoldására. Feladat. Tervezzünk olyan áramkört a fenti feladat megoldására, ahol az idő körülbelül (itt valami konstans szorzó megengedett), a terület pedig körülbelül . Ami számunkra érdekes és általában igaz, az egy bizonyos "osztozkodási'' tétel, ami azt mondja ki, hogy az adott feladat megoldására tervezett áramköröknél ez a két mennyiség csak egymás rovására növelhető. Tétel. Ha egy területű áramkör idő alatt dönti el két -hosszúságú 0‐1 sorozat egyenlőségét, akkor Bizonyítás. Képzeljünk el egy áramkört, és vágjuk függőlegesen két részre a chipet: az egyik rész tartalmazza az , a másik pedig az jeleket fogadó processzrokat. Mivel a két hosszúságú sorozatot valahogy ,,össze kell hozni'', a döntés meghozataláig ezen a vágáson legalább bitnek át kell jutnia. Erre összesen taktusnyi idő áll rendelkezésre, van tehát olyan lépés, amikor egyszerre bit jut át a vágáson, amihez persze legalább darab drótra van szükség. Ez persze csak annyit ad, hogy . De most menjünk tovább. Vágjuk most el a chipet az első vágástól -gyel balra. Ekkor és persze egy oldalra kerülhetnek, de az így szétvágott chipben a két rész egyike sem tud semmit a "másik fél'' hosszúságú sorozatáról , ill. , így az előzőek szerint ezt a vágást legalább darab drótnak kell kereszteznie ahhoz, hogy taktus után megszülethessen a döntés. Ugyanez persze arra a vágásra is igaz, amit az elsőtől -gyel jobbra húzunk. Ha most egyesével tekintjük jobbra és balra a vágásokat, akkor a drótok összhosszára ‐ és itt csak a függőlegesen átvágott drótokat számoltuk ‐ a következő alsó becslés adódik: A megadott két áramkör tehát ebben az értelemben optimális: értéke mindkét esetben . Valamilyen értelemben a két szélsőséget jelentik: legalább drótra már a darab bemenő jel miatt is szükség van, másfelől ‐ és ennek igazolása egy picit nehezebb ‐ még a legbonyolultabb huzalozással sem vihető a döntéshez szükséges idő alá. Jegyezzük még meg, hogy nyilvánvalónak vettük, hogy a két rész között legalább bit kommunikációjára van szükség. Itt kapcsolódik a kérdés az űrhajó problémájához. Ott láttuk, hogy ha nem törekszünk teljes biztonságra, akkor már lényegében bit is elegendő ‐ ez a megoldás azonban az integrált áramkörök tervezése során elesik, mivel a korábban leírt véletlen módszer alkalmazása jóval idő- és eszközigényesebb, mint ami az integrált áramkörök tervezésekor megengedhető. 3. A feladat általános megfogalmazása Sokszor segít, ha az adott problémát megpróbáljuk viszonylag általános módon megfogalmazni. A fenti feladatok két szereplője ‐ az űrhajó és a Föld, illetve a chipnek az és sorozatokat "ismerő'' részei ‐ külön-külön bizonyos, a másik fél által nem ismert információ birtokában "szeretnének'' valami együttes döntést hozni. Az általánosság megszorítása nélkül föltehető, hogy a két fél ‐ legyenek ők és ‐ egy-egy hosszúságú 0‐1 sorozatot ismer ‐ legyenek ezek és ‐ és ebből valamilyen -nal jelölt mennyiséget szeretnének kiszámítani. Egy játéknak is tekinthető a dolog a két fél, és között. Ilyen például a bridzs, amikor a két partner ismeri a saját lapját és a licit során az adott szabályok szerint kommunikálva el szeretnék dönteni, hogy kettejük lapjában benne van-e például a nagy szlemm. (A példa persze nem egész pontos, hiszen a másik két játékos licitálását is hallják). Az is feltehető, hogy ez a egyetlen bit ‐ az űrhajó feladatában például , ha és egyébként. Ezt az esetet jellemezhetjük egy táblázattal. A táblázat sorai az , oszlopai pedig a lehetséges 0‐1 sorozatainak felelnek meg ‐ esetünkben tehát darab sora és ugyanennyi oszlopa van a táblázatnak ‐ az -edik sor -edik mezőjében pedig az a érték áll, amelyet a két félnek valamilyen pár beszéd során meg kell határoznia, ha az az , a pedig az sorozatot ismeri. A teljes táblázatot ‐ mátrixot ‐ persze mindketten ismerik, csak azt nem tudják a beszélgetés kezdetén, hogy a másik fél számára melyik sor, illetve oszlop van megadva. Az űrhajófeladat mátrixa igen egyszerű szerkezetű: az átlóban -esek állnak, másutt pedig , hiszen föltehető, hogy a játék kezdete előtt és megállapodnak abban, hogy ugyanabban a sorrendben sorolják föl a sorozataikat. Látható, hogy bit elegendő a feladat megoldásához ‐ például úgy, hogy elküldi a sorának a számát ‐ ez -nek elegendő, hisz magát a mátrixot mindketten ismerik. Annak bizonyítására, hogy ennél kevesebb bit nem elegendő kiszámításához, "földönkívüli'' segédeszközhöz folyamodunk. Az űrhajónál maradva tegyük fel, hogy egy szuperlény, egy ET is belehallgat a beszélgetésbe, átlátja a helyzetet és szeretne segíteni a résztvevőknek a beszélgetés lerövidítésében. Nos, ha a két program nem azonos, akkor ET-nek könnyű dolga van. Ránéz a földi programra, ránéz a rakéta programjára és rögvest feltűnik neki, hogy a bit nem azonos a két programban. Közli az űrhajóval, hogy küldjék el ezt a bitet a földi központnak, hogy a két érintett fél is pillanatok alatt meggyőződhessen a hibáról. Ehhez lényegében a hibás bit sorszámát kell közölnie az űrhajóval, tehát a teljes hosszúságú bitsorozat helyett egy legfeljebb -jegyű szám nevét, ami körülbelül bit. Például ha , akkor ez kb. bit. A hibás bit sorszáma alapján aztán az űrhajó és a földi központ már ennek az egyetlen további bitnek az elküldésével meggyőződhet arról, hogy a program valóban megsérült. Mi a helyzet azonban akkor, ha a két program egyenlő. Tud-e az ET most is segíteni? Ha hisznek neki, akkor persze tud. A dolog azonban nemcsak bizalom kérdése. Mindkét félnek bizonyítékra van szüksége, ugyanúgy, mint az előbb. Azt állítom, hogy ilyenkor még az ET természetfölötti adottságai sem elegendők e mindkét fél számára meggyőző kommunikáció lerövidítéséhez. Vizsgáljuk a kérdést tetszőleges mátrixra. Az ET segítsége azt jelenti, hogy a két játékos, és bármely sorához és oszlopához van az ET-nek olyan üzenete, amelyik az sor és az oszlop metszéspontjában álló bit bizonyítéka mind az , mind pedig a számára. ET természetesen a mátrix mindegyik -esére bizonyítékkal tud szolgálni a feleknek. Egy adott üzenetére vannak a táblázatnak olyan sorai, illetve oszlopai, hogy és ezek bármelyike esetén a metszéspontban álló -es bizonyítékának fogadja el a üzenetet. Ekkor persze ezen sorok és oszlopok valamennyi metszéspontjában ‐ a mátrix ún. részmátrixában ‐ egyesek állnak. Ha ugyanis az valamelyik, a -hez tartozó sorát a egyik -hez tartozó oszlopa -ban, a másik pedig -ben metszené, akkor amennyiben az -nak ez az a sora, akkor számára az ET üzenete nem bizonyíték. Ha most az ET minden olyan -re és -ra, amelyre , legfeljebb bit hosszúságú bizonyítékkal tud szolgálni a felek számára, akkor az ő darab lehetséges üzenete alapján a fentiek szerint kijelölhető a mátrixnak legfeljebb darab olyan részmátrixa, amelyek minden eleme -es, és ezek a mátrix minden -esét tartalmazzák. Ha most az űrhajófeladat mátrixát tekintjük, akkor nyilvánvaló, hogy ebben a -es mátrixban, ahol a főátlóban -esek, máshol pedig -ák állnak, az -esek nem fedhetők le -nél kevesebb "csupaegy'' téglalappal, ET sem képes tehát bitnél rövidebb bizonyítékkal szolgálni egyenlőség esetén a feleknek. Az pedig nyilvánvaló, hogy ekkor ennél rövidebben saját erőből sem boldogulhatnak, hiszen ha ez lehetséges volna, akkor az ET ezt a beszélgetést közölhetné -val és -vel, akiknek a táblázat ismeretében a saját párbeszédükként elismerve ezt már az egyenlőség bizonyítékaként kellene elfogadniuk. 4. Egy fölső korlát ET eddig is jó szolgálatot tett, a továbbiakban se váljunk el tőle. Láttuk, hogy az "egyenlőség-probléma'' megválaszolásakor egyenlőtlenség esetén komoly segítséget nyújthat: hosszúságú bitsorozatokra hosszúságú bizonyítékkal szolgálhat a felek számára akkor, ha a két sorozat nem egyenlő. Nézzük a dolgot általában. Legyen megint a két játékos és , és játsszanak a -ákból és -esekből álló mátrixon. megkapja a mátrix egy sorát, a mátrix egy oszlopát és el kell dönteniük, mi áll a metszéspontban. Három mennyiséget vezetünk be. Legyen a minimális hosszúságú bitsorozat, amellyel a felek bármely sor és oszlop esetén eldönthetik, hogy mi áll a metszéspontban. (Az űrhajófeladatban, mint láttuk, , a triviális megoldásnál jobb nincs ‐ még ET számára sem.) Jelölje az ET által adható bizonyíték minimális hosszát akkor, ha a válasz és hasonlóan értelmezzük válasz esetén a mennyiséget. Az űrhajófeladatban volt. A különböző kommunikációs feladatokban ez a két szám nagyon eltérő lehet. Nyilvánvaló, hogy max alsó korlát -ra is. Egy meglepő tétel szerint viszont felső korlát, azaz ha ET így vagy úgy be tudja nekik bizonyítani a választ, akkor ők egymás között is elboldogulnak lényegében e két mennyiség szorzatával. Ezt a tételt nem bizonyítjuk. 5. Játék egy fán Az alábbi példában a játék speciális szerkezetű halmazon folyik: egy pontú gráfon, mégpedig egy fán, tehát egy olyan gráfon, amelyik összefüggő és nem tartalmaz kört. Mindkét játékos ismeri a fát. Mindketten kapnak egy-egy részfát a gráfból, az -t, pedig az -t. A másik részfáját egyikük sem ismeri. Az a feladatuk, hogy eldöntsék, van-e a két részfának közös pontja. Nézzük először azt a változatot, amikor ET is résztvesz a játékban. Ha a két részfának van közös pontja, akkor nincs más dolga, mint ennek a pontnak a nevét közölni -val és -vel, akik ellenőrizhetik, hogy a pont benne van a részfájukban. A gráf pontjainak száma , így egy pont megnevezéséhez bit szükséges. (Valójában , de a továbbiakban az egészrész jelét elhagyjuk.) Így . Akkor is könnyen boldogul ET, ha a két részfa nem metszi egymást. Ekkor ugyanis van olyan él ‐ hacsak nem üres a két részfa valamelyike, ‐ amelyiket elhagyva az fa két összefüggő részre ‐ komponensre ‐ esik szét, melyek egyike az -t, a másikuk pedig az -t tartalmazza. Ha ET ezt az élt közli a felekkel, mégpedig irányítással, például úgy, hogy az elhagyott él az részfája felé mutasson, akkor ennek alapján és ellenőrizhetik, hogy részfáik különböző komponensekben vannak, és így ET közleménye számukra a fa ismeretében bizonyíték. Ekkor ET-nek összesen közleménye lehetséges: a fa darab megfelelően irányított éléhez és még kettő arra az esetre, ha vagy üres. Ez megfelelő kódolással bitet jelent, azaz Mit tegyenek a játékosok az ET segítsége nélkül? Nos, legrosszabb esetben egyikük pl. ‐ elmondhatja -nek, hogy melyik az ő részfája (az űrhajófeladatban ennek felel meg a teljes program visszaküldése). Az a helyzet, hogy egy pontú fának általában nagyon sok ‐ -ben exponenciálisan sok ‐ részfája van. Ezzel kapcsolatos az alábbi feladat. Feladat. Bizonyítsuk be, hogy ha egy pontú fában nincsen másodfokú pont, akkor a fának legalább darab részfája van. Ennek a ténynek az a következménye, hogy az ilyen fák esetén az a triviális eljárás, hogy valamilyen kódolással megmondja -nek az részfáját, a legrosszabb esetben legalább bitet igényel. bit persze minden fa esetében elegendő, hiszen ez darab közleményt tesz lehetővé, tehát például így a gráf szögpontjainak valamennyi részhalmaza felsorolható, vagyis az összes részfa is. Van olyan fa, ahol a triviális eljárás során erre szükség is van, mert itt a csúcsok majdnem minden részhalmaza részfát jelöl ki. Ilyen az ún. csillag (3. ábra), amelynek darab részfája van. Most azonban a triviális eljárásnál jóval hatékonyabb módszer is megadható. Válasszon az egy pontot az ő részfájából és küldje ezt el -nek. Ha , akkor ezt látja és egyetlen további bitben megüzeni -nak. Ha nem, akkor mivel az gráf összefüggő, -ből az bármely pontjába vezet út ‐ és csak egy, mert az fa. Minden ilyen úton tekintsük a legelső -beli pontot. Azt állítjuk, hogy ez a pont egyértelmű: Valóban, ha és két ilyen "belépési pont'', akkor mivel fa, és között az -ben is vezet út (4. ábra) és így -ben van kör, ami nem lehet.  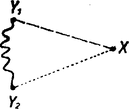 Küldje tehát vissza ezt az -ből az ő részfájába vezető úton egyértelműen meghatározott "belépési pontot'' -nak. Ha , akkor megint készen vagyunk, tudja a választ. De akkor is tudja a választ, ha . Ekkor ugyanis a két részfának nem lehet közös pontja. Ha ugyanis volna ilyen közös pont (5. ábra), akkor ez az megválasztása miatt nem lehet rajta az és között haladó -beli úton ‐ volt a belépési pont ‐ másfelől és is összefüggők, így létezik -beli és -beli út, vagyis az gráfban van kör. Ez pedig ellentmondás. 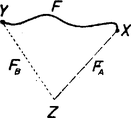 Az üzenetváltás során a játékosok két pont nevét közölték egymással. Ez pont esetén az ismert módon bittel megoldható, így ebben a feladatban . Azt állítom másfelől, hogy most A -ra kapott korlátok most közelíthetők. A fenti eljárás ügyesebb megszervezésével egy -hez közeli felső korláthoz juthatunk. Ehhez némi előkészítő munkálatok szükségesek. Arról van szó, hogy a fa csúcsait nem akárhogyan számozzuk meg, hanem az adott gráf szerkezetével összhangban. Hogy ez pontosan mit jelent, azt az alábbi segédtétel mondja el az számokkal. Segédtétel. Minden pontú fa csúcsai megszámozhatók úgy, hogy ha -ből elhagyjuk az számú csúcsokat, ‐ azaz "felvágjuk'' a fát ‐ akkor a kapott körmentes gráf ‐ ún. erdő ‐ komponenseinek legfeljebb csúcsa van. A fenti számozás szerinti vágások tehát "egyenletesen'' vágják szét a fát. A bizonyításhoz megmutatjuk, hogy minden pontú fában van olyan pont ‐ hívjuk ezt a fa "középpontjának'' ‐ amelyet elhagyva a fából az legfeljebb pontból álló komponensekre esik szét.  Tekintsük ugyanis a fában azt a pontot, amelyet elhagyva a kapott komponensek elemszámának maximuma minimális (6. ábra). Ha egy ilyen maximális elemű komponens, akkor azt állítjuk, hogy -nek legfeljebb pontja van. Tegyük fel, hogy ez nem igaz és a -ben több, mint pont van. Ekkor a további komponenseknek együttvéve még az ponttal együtt is -nél kevesebb pontja van. Vegyük most vissza a gráfba az elhagyott pontot, és hagyjuk el az -ből a -be vezető él másik, végpontját. Ekkor a komponensek az -mel együtt egyetlen, -nél kevesebb pontú komponenssé állnak össze. A komponensből a elhagyása után egy, a -nél eggyel kevesebb pontú gráf lesz, és így akár összefüggő marad, akár nem, az helyett a -t elhagyva csökken a komponensek elemszámának maximuma. Ez ellentmond az kiválasztásának, tehát a -ben valóban nem lehet -nél több pont. Ezután megadjuk a Segédtételben leírt számozást. Kapja az egy középpontja az -es sorszámot. A -es sorszámú pont az -es elhagyása után keletkező legnagyobb komponens középpontja legyen, és így tovább, ha már megvannak az sorszámú csúcsok, akkor a sorszámot a már megszámozott pontok elhagyásával keletkező legnagyobb komponens középpontja kapja. Feladat. Bizonyítsuk be, hogy ez a számozás megfelelő. Nézzük most meg, hogyan segíthet -nak és -nek ez a számozás. Az eljárás kezdetén az gráffal együtt rögzítsenek egy ilyen számozást, majd külön-külön válasszák ki az és az részfájukat. Az első lépésben kiválasztja a részfájába eső legkisebb ‐ mondjuk ‐ sorszámú csúcsot és ezt a értéket elküldi -nek. (Ha az üres, akkor küldjön -át: ekkor készen vannak.) A ismeretében a tudja, hogy nem tartalmazza a -nál kisebb sorszámú pontokat. Ezeket tehát elhagyhatja az fából, benne lesz valamelyik komponensben. Mivel az egyik csúcsát is ismeri ‐ ez a sorszámú pont ‐ így azt is tudja, hogy melyik ez a bizonyos komponens. -t természetesen az is ismeri. Ha most az részfa nem metszi az komponenst, akkor -nak és -nek nincsen közös csúcsa, és ezt egyetlen további bittel jelezheti -nak. Ha az metszi -t, akkor legyen , az -nek az -ba eső része. is fa, és így az eredeti eljárás első lépése utáni helyzet állt elő, csak a játék fájának a mérete csökkent és a fája módosult: és most a segédtétel szerint legfeljebb csúcsú fa részfái, és ezt és mindketten tudják. Ha visszaküldi az előző eljárásban megadott belépési pontot -nak, akkor az ott leírtak szerint ebből már tudni fogja a választ. A fenti számozás most már lehetővé teszi, hogy ne az eredeti, -beli sorszámát küldje vissza, hisz az ehhez szükséges bit nem hasznosítja azt a mindkét fél számára rendelkezésre álló információt, hogy és is a "kicsi'' -ban vannak. Ha az -beli pontok sorszámai és az pont ezek közül nagyság szerint az -edik, akkor -nak csak az értékére van szüksége ahhoz, hogy az eredeti számozás alapján megkeresse az komponensben az pontot. -et és -t ismerve ezután már az előző eljáráshoz hasonlóan dönteni is tud. Vizsgáljuk meg az üzenetváltás hosszát. Az a értékét bitben küldi el -nek, aki miatt bitben küldheti vissza az értékét -nak. Ez pedig összesen mindössze bit. Egy elvi megjegyzést szeretnék még fűzni a fentiekhez. Az elhangzott példákban a felek a párbeszédek során mindig jóelőre megállapodtak az egyes üzenetek hosszában, ami elég természetes követelmény. Ez ugyan olykor látszólag gazdaságtalan megoldást jelent, hiszen ha például jegyű számokat kell üzengetni, akkor a kicsi -est ugyanúgy jegyű sorozat kódolja, mint a nagy számokat. A legutolsó példában viszont, ahol első üzenete a értéke, a játékosok nem tudnak előre megállapodni az üzenet hosszában, hisz a értékét nem ismerik. Ha , , akkor nem teheti meg, hogy csak az bitsorozatot küldi el -nek és vár. ugyanis ekkor nem tudja, valóban vége van-e üzenetének. Egy hosszú csend itt nem megoldás, hiszen az tulajdonképpen egy extra jel, és pedig csak a -t és az -est ismeri el jelként. Nem megoldás az sem, hogy valamilyen "üzenet vége'' speciális bitsorozatban állapodnak meg, hisz előre nem látható hosszúságú üzenetnél nem lehet tudni, hogy az érkező jelek nem a valódi üzenethez tartoznak-e. persze elküldhetné az értéke alapján félreérthetetlen bitsorozatot, hisz nagyságrendjét mindketten ismerik, de ekkor helyett lesz az első üzenetének hossza. Ha viszont egy ‐ a mindkét fél által ismert és előre rögzített hosszúságú ‐ sorozattal kezdi az üzenetét, amelyben közli a méretét, akkor az első jegyből álló számból már tudja, hogy a közlemény második, a -t tartalmazó része milyen hosszú. A példában tehát az üzenete a -ra . A második lépésben már nyugodtan használhat méretű bitsorozatokat minden kommentár nélkül az kódolására, hiszen a párbeszédnek ebben a fázisában már mindketten ismerik a értékét. Ez annyit jelent, hogy a párbeszéd hossza bittel nő, ami azonban a taghoz képest kicsi. Végül azt kaptuk tehát, hogy a feladatra A kommunikáció bonyolultságának megismerésében még csak a kezdet kezdetén járunk. Nagyon keveset tudunk például arról, hogy mi történik -nél több résztvevő esetén. Azt sem értjük igazán, hogy miért segít a véletlen használata az űrhajós példában, és miért nem segít más, hasonló feladatok esetén. A kommunikáció, hírközlés korunk egyik fő jelensége, és bizonyos, hogy még sok izgalmas matematikai problémával fog szolgálni. |